[JavaScript] 프로그래머스 숫자의 표현 풀이

🔍 연습문제 > 숫자의 표현

클릭해서 문제 전체 보기🔼

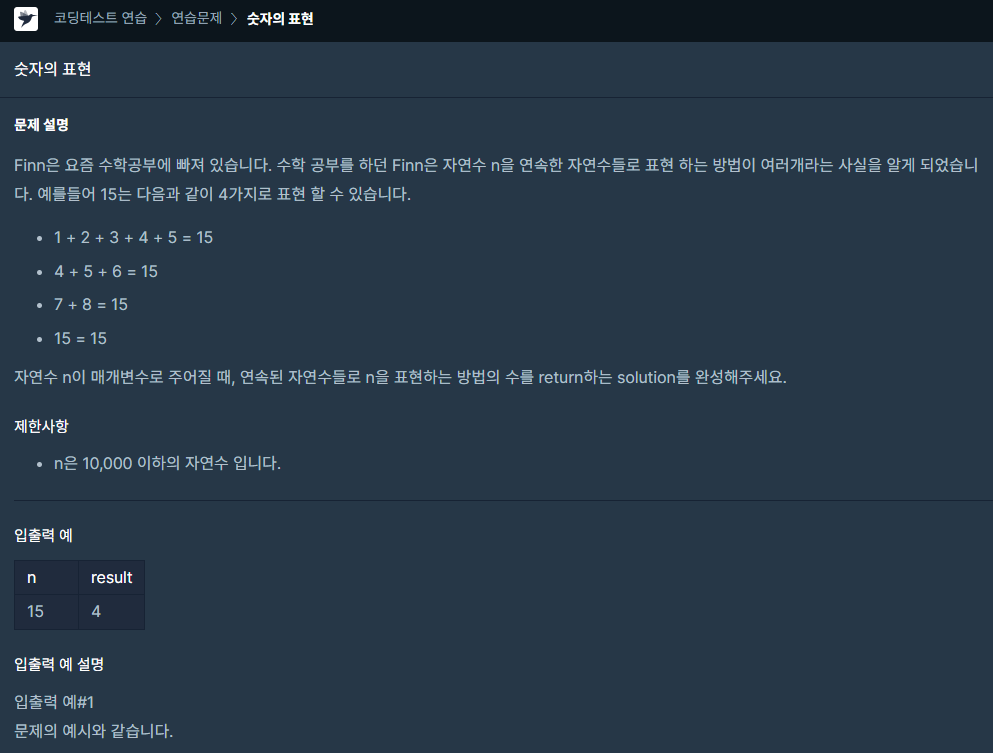
📖 풀이 코드

function solution(n) {
    let count = 0;
    let half = Math.ceil(n / 2);
    let arr = []
    
    if(n % 2 != 0 && n != 1) count++;
    for(i=1; i<=half; i+=2) {
        if(n % i == 0) count++;
    }
    return count;
}

📢 풀이 설명
자연수를 연속된 자연수의 합으로 표현하는 방법의 수 = 주어진 수의 홀수인 약수 개수를 이용하는 문제

약수란 나누어떨어지는 수를 의미하므로, 자기 자신을 제외하고는 주어진 값의 절반 이하의 숫자들로만 이루어져있다.
n의 값이 짝수가 아니면서 1도 아니라면, 1이상의 홀수라는 뜻이므로 count를 1 올린다.
그 후, for문을 이용해 n이 i가 홀수일 때 나누어떨어지면 count를 올린다.
n의 절반인 half까지 for문을 돈 후, 최종적인 count를 반환한다.

=> 15의 약수는 총 4개(15, 5, 3, 1)이고, 이 중 홀수도 4개이다. 따라서 연속된 자연수들로 표현할 수 있는 방법의 수는 4가지이다.
즉, 약수의 개수 중 홀수인 것의 개수를 출력하는 문제와 같다.

📖 잘못된 풀이 코드

function solution(n) {
  let count = 1;
  let half = Math.ceil(n / 2);

  for (i = 0; i < half - 1; i++) {
    let k = half - i;
    let t = half - 2 - i;
    let sumOne = k ** 2 + k;

    while (t >= 0) {
      let sumTwo = t ** 2 + t;
      if (2 * n - sumOne == -1 * sumTwo) {
        count++;
        break;
      }
      t--;
    }
  }

  return count;
}

채점 결과: 정확성 모두 통과, 효율성 모두 불통과

📢 풀이 설명
n의 절반 이상의 값을 더하면 n의 값을 넘으므로, 이하의 값들로만 표현할 수 있어 half를 설정했습니다.
연속되는 수는 수열의 합으로 나타낼 수 있다고 생각해서, 수열의 합 공식을 이용하여 풀었습니다.

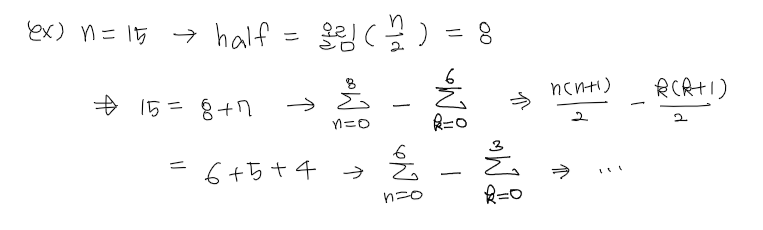
계산을 너무 많이 반복해야 해서 시간초과가 발생했다고 생각합니다.