출처: DSBA 연구실 유튜브 와 DSBA 연구실 강의자료 를 참고하면서 스터디를 진행하였습니다.

주제: Anomaly Detection_Distance-based

---

1. K-Nearest Neighbor-based Anomaly Detection

---

1.1. K-Nearest Neighbor-based Approach

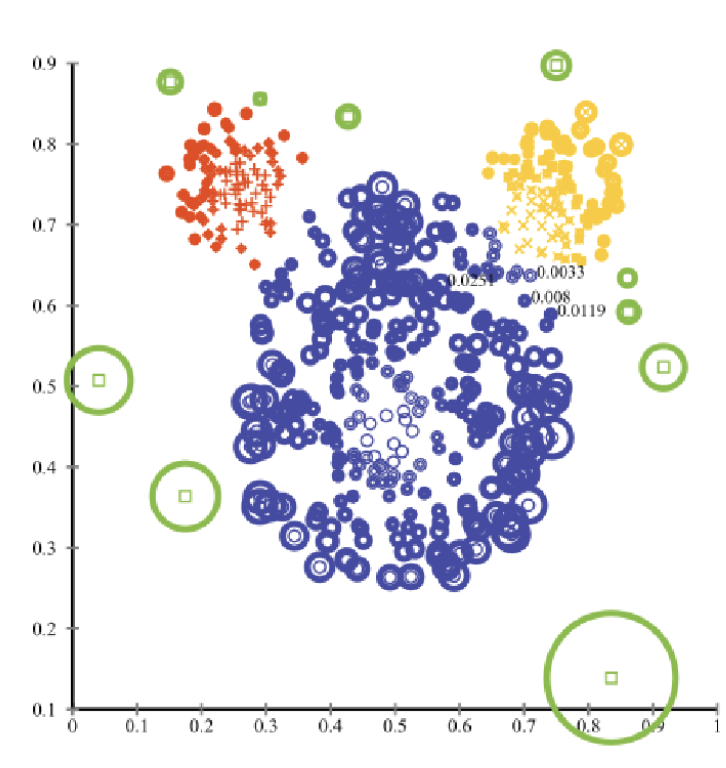
Assumption

• 이상치에 해당하는 객체들은 다른 객체들과의 거리를 계산했을 때 굉장히 멀리 떨어져 있음.

• 이상치는 정상 데이터에 비해 거리가 훨씬 길 것이라고 전제

• 정상 데이터(Normal class)에 대한 사전 분포 가정 X

• 단순히 데이터로부터 가까운 객체들 간의 거리만을 계산해서 그 거리값이 길면 이상치 score일 확률 👆 / 거리값이 낮으면 이상치 score일 확률 👇

---

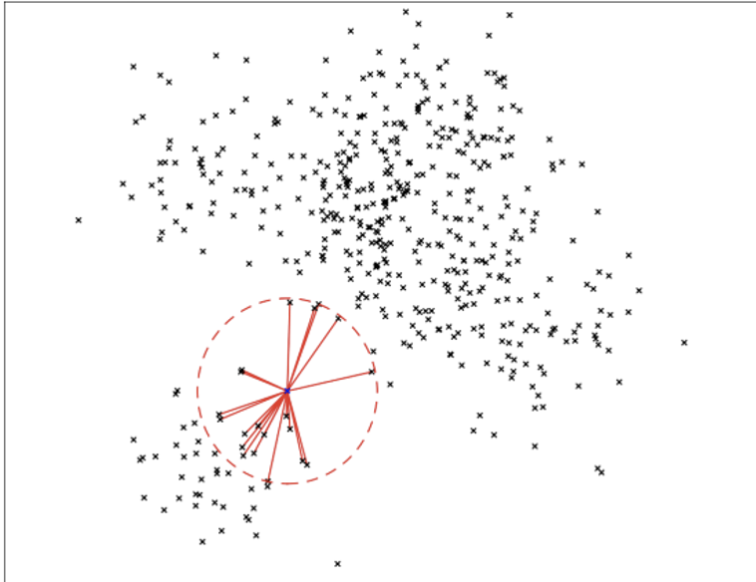
Various distance information (거리 계산법)

• Maximum distance to the k-th nearest neighbor

$d^k_{max} = \kappa(\mathbf{x}) = \lVert \mathbf{x} - z_k(\mathbf{x}) \rVert$

• Average distance to the k-nearest neighbors

$d^k_{avg} = \gamma(\mathbf{x}) = \frac{1}{k} \sum^k_{j=1} \lVert \mathbf{x} - z_j(\mathbf{x}) \rVert$

• Distance to the mean of the k-nearest neighbors
  - 이웃들의 공간상 무게중심(평균)을 구한 뒤 무게중심까지의 거리

$d^k_{mean} = \delta(\mathbf{x}) = \lVert \mathbf{x} - \frac{1}{k} \sum^k_{j=1} z_j(\mathbf{x}) \rVert$

1.2. Comparison average, and mean distance

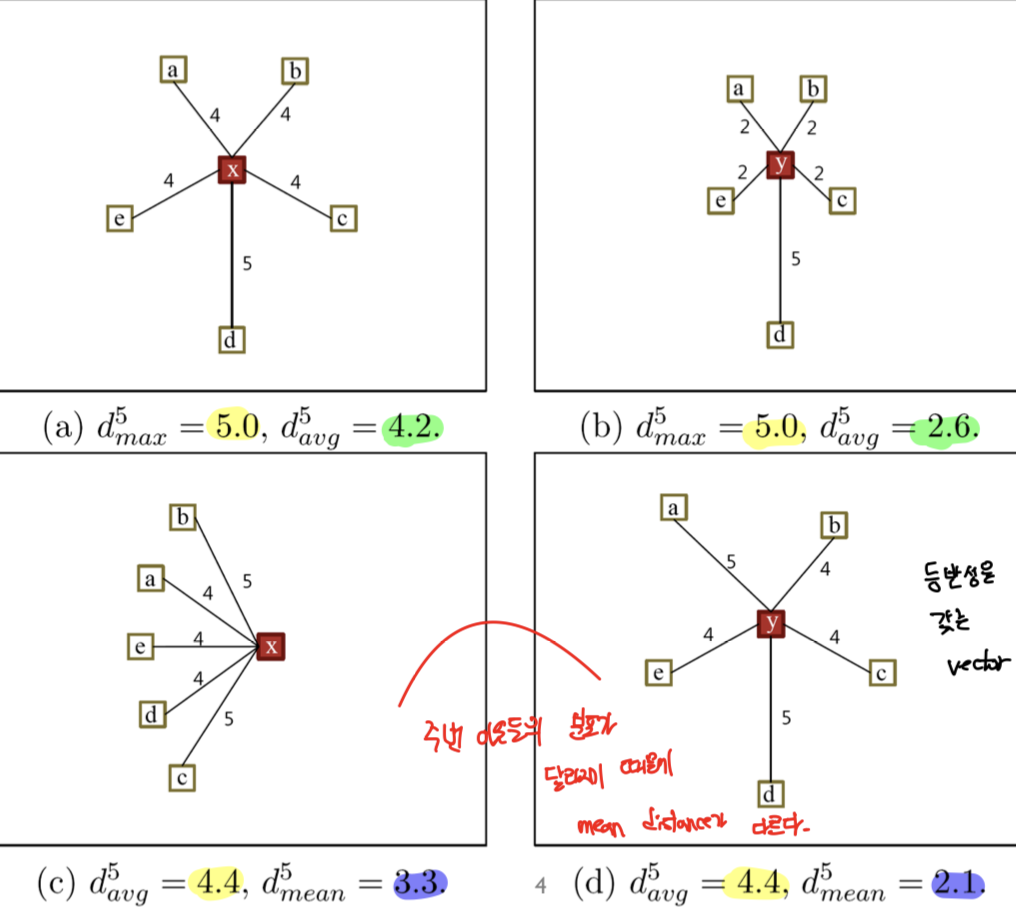
• 주변 데이터가 어떻게 분포하느냐에 따라서 거리 distance socre들이 각각의 장단점을 갖음.

• 주변 이웃들의 분포가 달라지기 때문에 mean distance가 달라짐.

---

1.3. Counter example of the previous anomaly scores

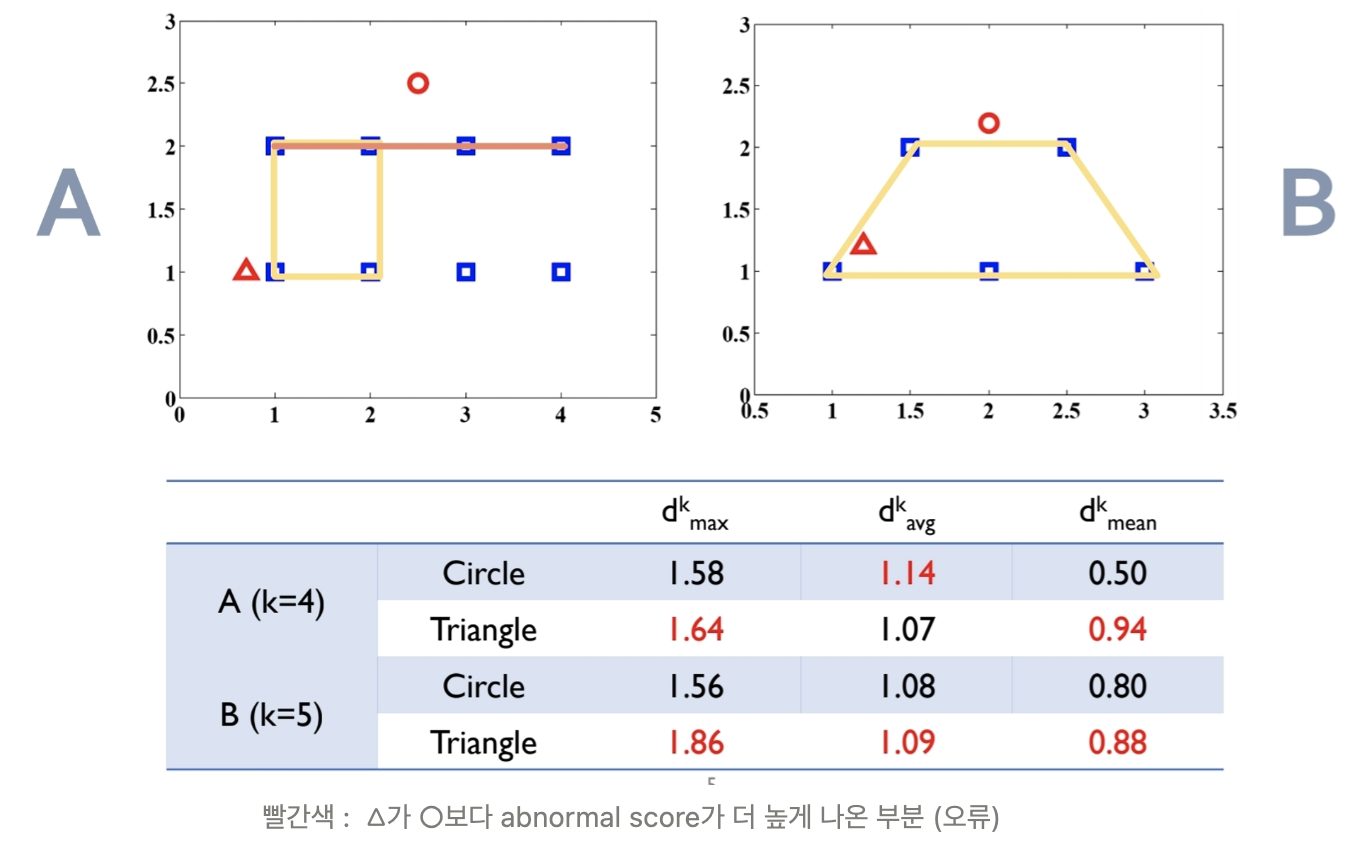
Idea

• '이상치가 아닌 정상 데이터라면, 나의 이웃들 polygon 안에 들어와야 되지 않을까?' 라는 아이디어에서 시작

• normal data가 이웃들의 polygon안에 들어와야 한다면?
  - A와 B case에서는 △가 ○보다 abnormal score가 더 낮아야 함.
  

Consider additional Factor

• 데이터를 감싸는 폴리곤을 만들어서, 폴리곤까지의 거리를 구함.

• 목적 함수: 개별적인 객체를 이웃들로 정확하게 reconstruction하는 w를 찾음.

$\min_w(d^k_{c-hull}(\mathbf{x}))^2=\lVert \mathbf{x}_{new}-\sum^k_{j=1}\mathbf{w}_i z_j(\mathbf{x})\rVert^2$

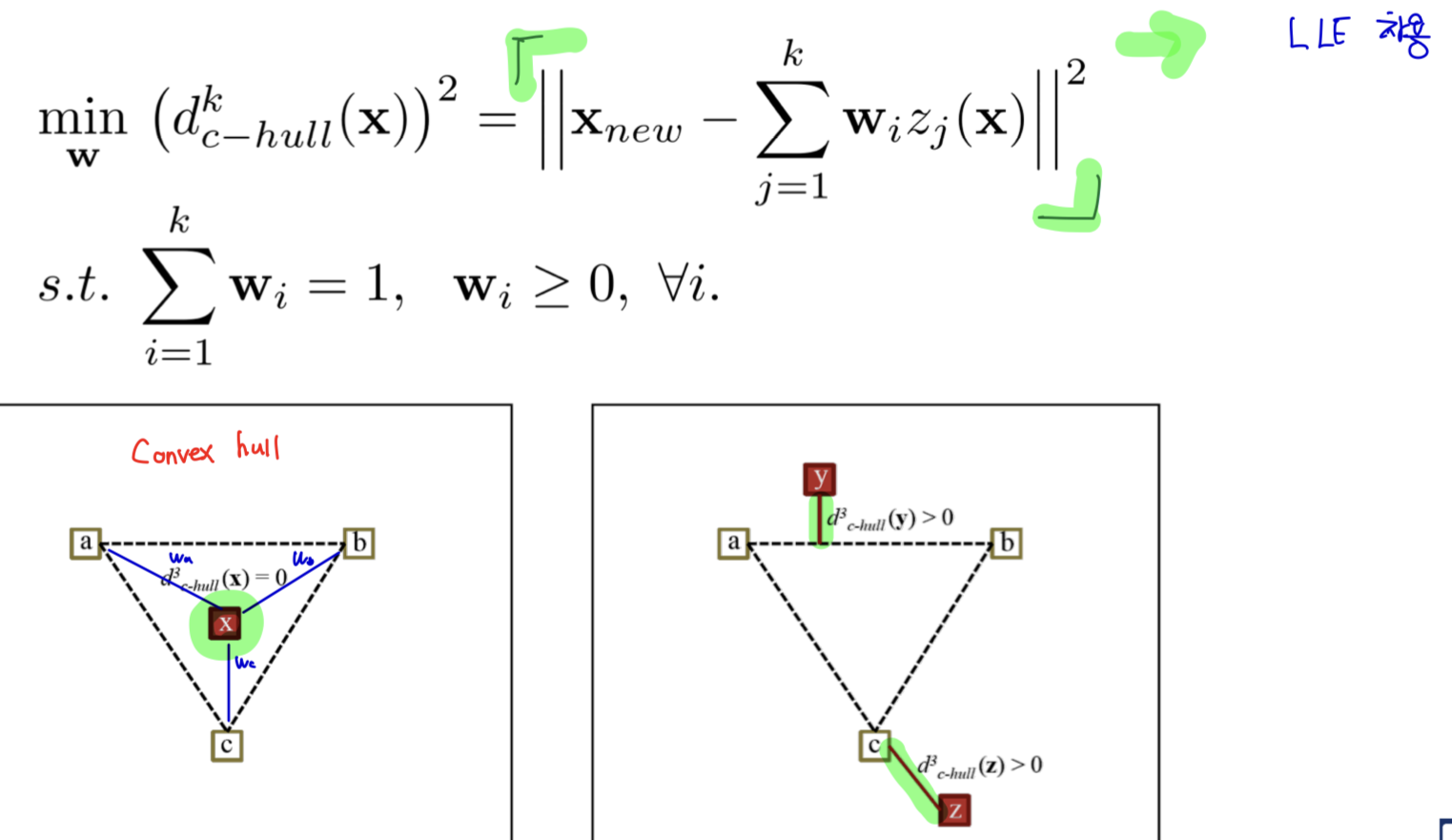
• 왼쪽 그림은 개별적인 객체가 polygon 안에 있는 경우이기 때문에, Convex distance = 0임.

• 오른쪽 그림은 객체가 polygon 밖에 있으면 Convex distance = 가장 가까운 선분에 수선의 발을 내렸을 때 길이임.

Combine the average distance and convex distance

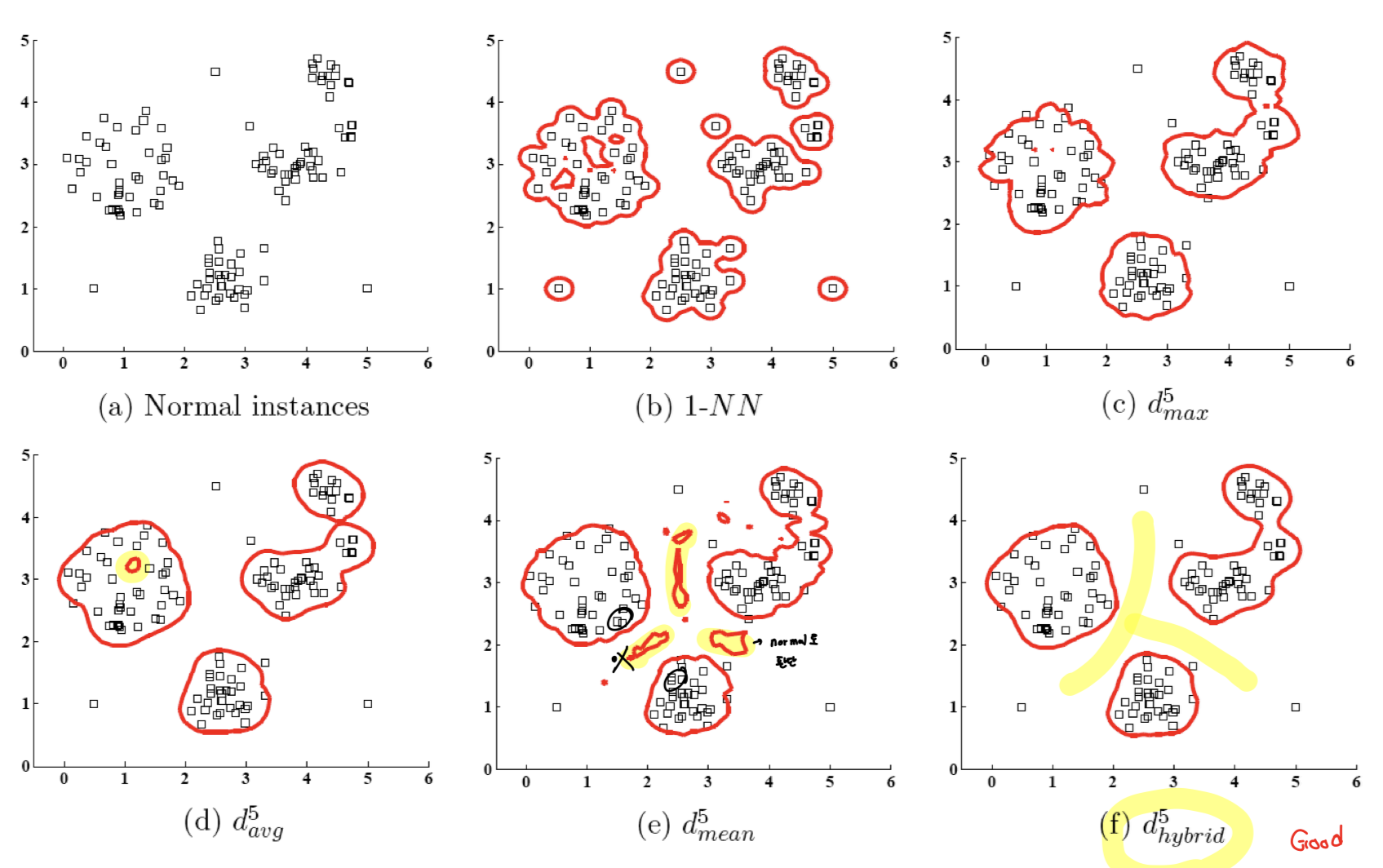
• Average distance
  : Average distance는 밀도가 낮으면 구멍이 뚫리는 상황 발생

$d^k_{avg} = \gamma(\mathbf{x}) = \frac{1}{k} \sum^k_{j=1} \lVert \mathbf{x} - z_j(\mathbf{x}) \rVert$

• Convex distance to its neighbors (보정을 위한 factor)

: Mean distance는 특정한 밀도가 높은 영역 중간에서 normal data로 잘 못 판별되는 상황 발생

$d^k_{c-hull} = \lVert \mathbf{x}-\sum^k_{j=1} \mathbf{w}_i z_j(\mathbf{x})\rVert$

• Hybrid distance

: Average를 기본적으로 사용하는데, Convex를 보정에 활용하는 형태
Hybrid distance는 Average distance와 Mean distance의 단점 보완

$d^k_{hybrid} = d^k_{avg} \times \left(\frac{2}{1+\exp (-d^k_{c-hull})}\right)$

📌 Polygon 안에 있으면, Convex가 0이므로 분모가 1이 되어 Average 그대로 사용

📌 Polygon 밖에 있으면, Convex가 0보다 커지면 분모가 2보다 작아지므로 Average distance에 penalty처럼 작용하는 것

---

2. Clustering-based Approach

2.1. K-Means clustering-based

• 가장 가까운 군집과의 거리조차 멀다면 해당 객체를 이상치로 판별함.

• 군집화 기반 알고리즘 (DBSCAN)
  : 군집화를 하는 과정에서 군집에 할당되지 않으면, 전부 outlier가 됨.

Two anomaly scores by KMC

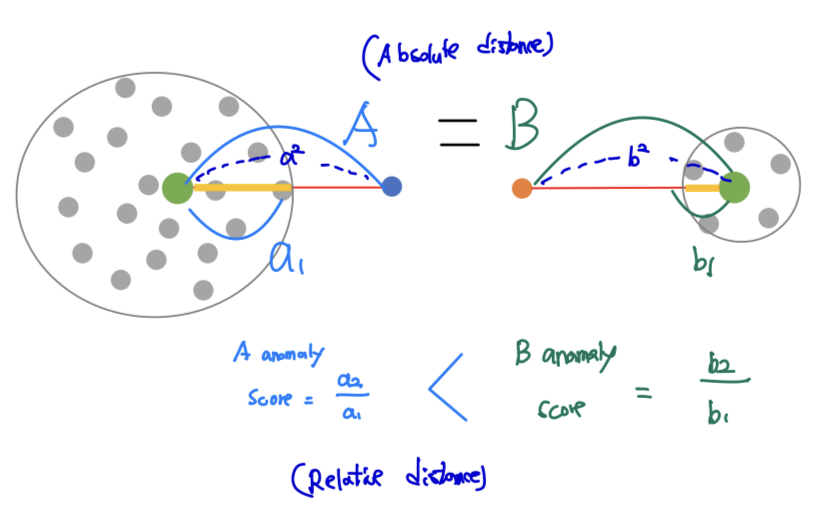
• Absolute distance
  : 가장 가까운 centroid 계산 A = B

• Relative distance
  : 군집의 반지름 대비 centroid 계산 → $A = a2/a1 < B = b2/b1$

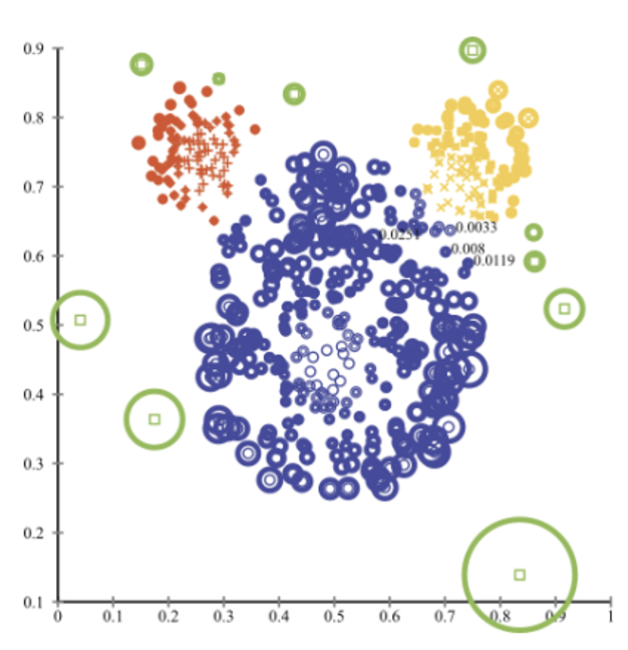
• 군집에서 멀리 떨어진 객체일수록 반지름의 크기(abnormal score)가 크게 나타남.

---

3. Principal Component Analysis-based Anomaly Detection (PCA)

• 주성분 분석(Principal Component Analysis, PCA) 기반 이상 탐지
  : 데이터의 주요 패턴을 학습하고 이러한 패턴에서 크게 벗어난 데이터 포인트를 식별하는 데 사용
  -> PCA 기반 이상 탐지는 데이터의 복잡성을 줄이고, 주요 특징을 유지하며, 이상 값을 효과적으로 식별함
  

• Purpose: maximize the variance after projection

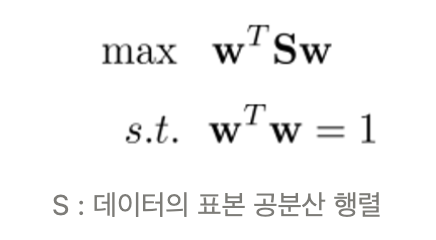
• Solution

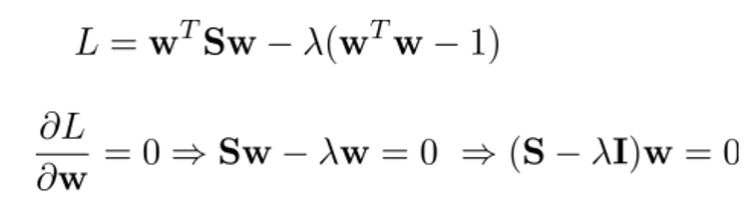
PCA as an anomaly detector

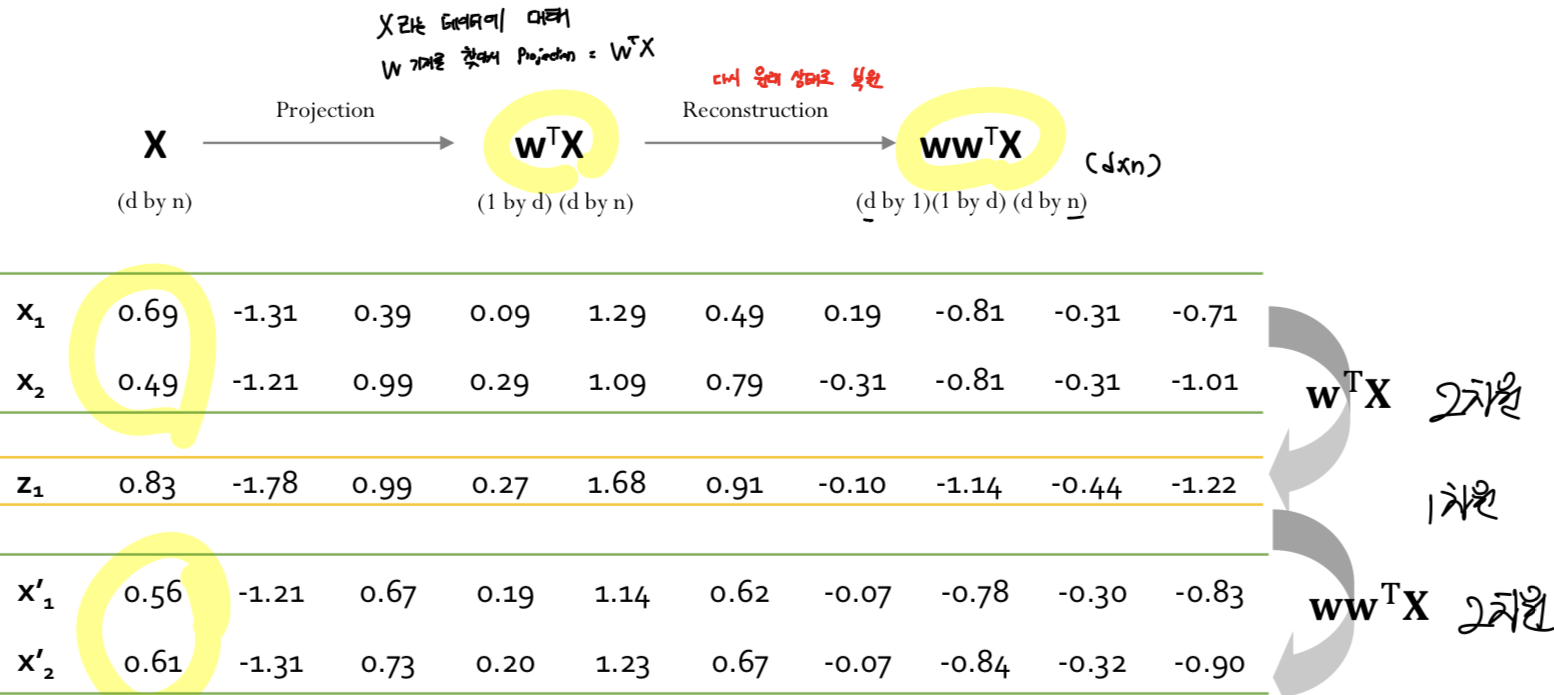
• 정상 데이터라고 하면, 전과 후가 같음

• 비정상 데이터라고 하면, Reconstruction 했을 때 오차가 크게 나타날 것임 (패턴이 파악되지 않으면)

$\text{error}(x) = \lVert\mathbf{x}\rVert^2 - \lVert\mathbf{w}^{\intercal}\mathbf{x}\rVert^2$

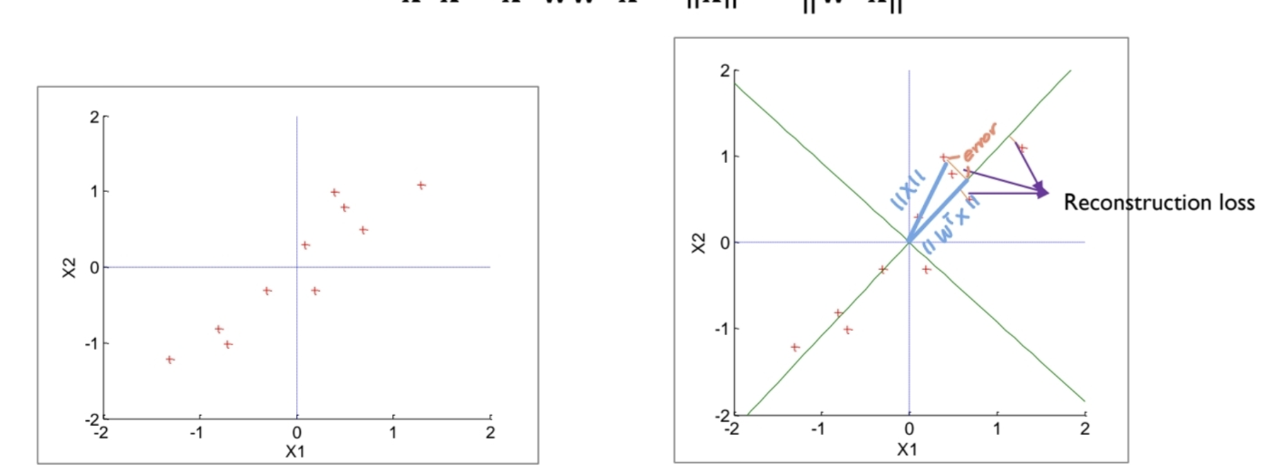
Graphical interpretation

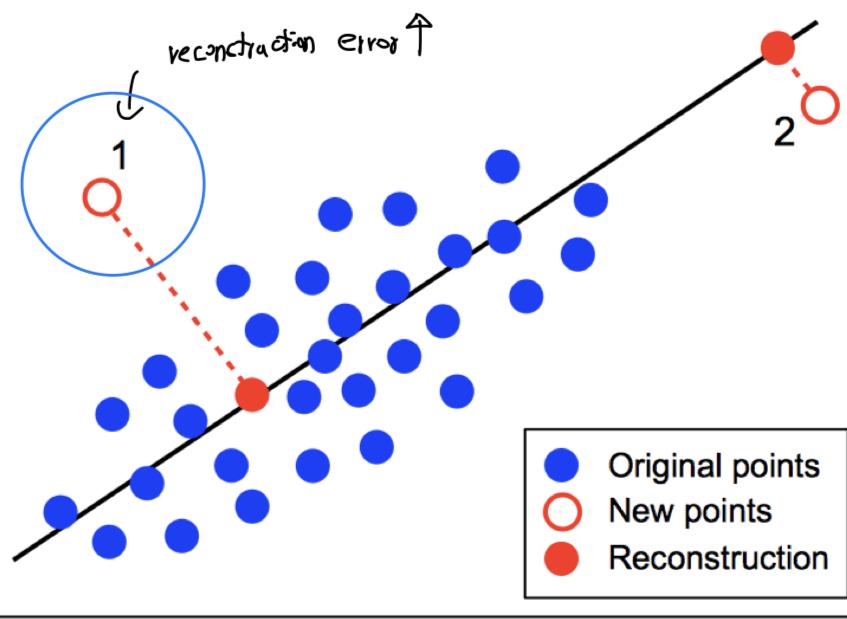
• 1번 data point의 Anomaly score > 2번 data point의 Anomaly score

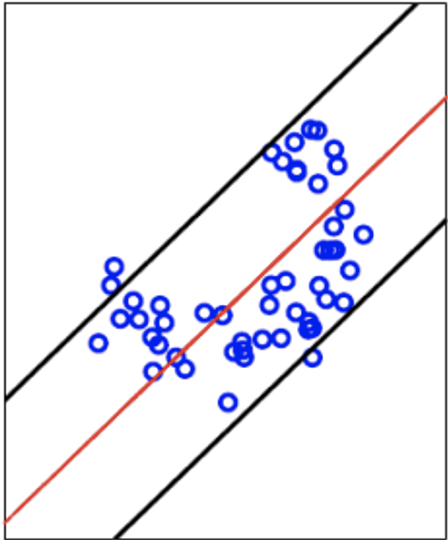
• 반달 형태의 normal data를 이용해서 첫 번째 주성분을 찾으면 빨간색으로 표시된 부분이 나옴.

📌 정리

• PCA는 데이터의 차원을 축소하여 주요 패턴을 찾음.
  데이터의 차원이 줄어들면 이상 탐지가 더 쉬워지며, 계산 비용이 줄어듦.

• 분산 최대화(Variance Maximization)
  : PCA는 데이터의 분산을 최대화하는 방향으로 새로운 축을 찾음
  이렇게 하면 데이터의 주요 특징이 유지되며, 이상 값이 더 잘 드러남.

• 선형 변환(Linear Transformation)
  : PCA는 선형 변환을 사용하여 데이터를 새로운 좌표 공간으로 매핑함.
  이 새로운 공간에서는 주성분 축을 따라 데이터의 분산이 최대화됨.

• 재구성 오류(Reconstruction Error)
  : PCA는 데이터를 낮은 차원으로 압축한 후 다시 원래의 차원으로 복원함.
  이 과정에서 발생하는 오차(재구성 오류)를 측정하고, 이 오차가 큰 데이터 포인트를 이상 값으로 식별함.

• 이상 탐지(Anomaly Detection)
  : 재구성 오류가 특정 임계값보다 큰 데이터 포인트는 이상 값으로 분류됨.
  이는 이러한 포인트가 주성분 축을 따라 주요 패턴에서 크게 벗어났음을 나타냄.

---

🎯 Summary

• 이 강의의 첫번째 부분에서 교수님께서 해주신 말씀이 기억에 남는다.

"지금 읽고 있는 논문들을 어디에 써먹을 수 있을지는 논문을 읽을 때는 모른다. 하지만 나중에 분명히 사용될 상황이 올것임을 믿고 닥치는대로 읽어라"

요즘 논문 리뷰를 안하고 있었는데, 나에게 채찍질 같은 말씀이었다. 교수님의 말씀을 신뢰하며 논문을 열심히 읽어야겠다.

• KNN, Clustering, PCA 등 머신러닝에서 배웠던 개념들을 다시 복습할 수 있어서 좋았음.

• 강의자료와 유튜브를 무료로 볼 수 있게 한 DSBA 연구실에 감사의 인사를 전합니다.

📚 References

• Youtube

• https://youtu.be/diEYxlkcwFM?si=D_f0eps4b7vRchkj, DSBA 연구실 유튜브

• 강의 자료

• https://github.com/pilsung-kang/Business-Analytics-IME654-/blob/master/03%20Anomaly%20Detection/03-5_Anomaly%20Detection_Distance-based.pdf, 강필성 교수님 github