출처: DSBA 연구실 유튜브 와 DSBA 연구실 강의자료 를 참고하면서 스터디를 진행하였습니다.
주제: Anomaly Detection: Local Outlier Factor (LOF)
1. Local Outlier Factors (LOF)
- 밀도 기반 이상치 탐지의 연장선에 있음.
- 어떤 객체가 주어졌을 때, local density를 고려해서 정의를 하자!
- 데이터 포인트의 지역적 밀도와 그 주벼 데이터 포인트의 밀도를 비교함으로써 이상치를 탐지함.
- LOF는 데이터 포인트의 극소적 밀도 변동을 감지하여 클러스터 내부의 밀도가 높은 지역과 낮은 지역을 구별 할 수 있음.
📊 알고리즘의 단계
1. 거리 계산
2. Reachability Distance 계산
3. Local Reachability Density (LRD) 계산
4. LOF 계산
📌 장점
1. 비모수적
- 데이터의 분포에 대한 가정 필요X
2. 국소적 특성
- 데이터 포인트의 국소적 밀도를 기반으로 이상치 탐지하기 때문에 다양한 밀도를 갖는 클러스터에서도 잘 작동함.
*국소적 밀도
: 데이터의 특정 지역 or 부분에서의 데이터 포인트의 밀도
=> (바뀐점) 특정 데이터 포인트 주변의 데이터 포인트의 수와 그 밀도를 기반
=> (기존) 전역적인 밀도 기반 이상치 탐지 방법은 데이터셋 전체의 밀도를 기반으로 함.
📌 단점
1. 계산 복잡도
2. 하이퍼파라미터 선택
- 선택한 이웃의 수 k에 따라 크게 달라질 수 있음.
3. score가 normalization 되어 있지 않음.
=> 같은 dataset에서는 LOF score가 크면 클수록 이상치일 확률 up
=> dataset이 달라지면, 단순히 이상치 score의 절대값을 가지고 이상치의 정도를 비교하는 건 위험함.
1.1. Definition
1. k-distance of an object p
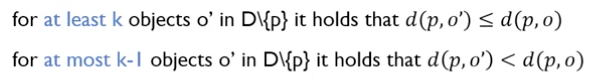
- 거리에 대한 정의
- 여기서 란 와 의 거리를 의미함.
- 를 만족하는 최소한 k개의 o'이 있어야 됨.
- 최대로 k-1개에 대해서는 를 만족해야 함.
- "Simply it is the distance to the k-th nearest neighbor considering ties."
📌 동률이 존재했을 때, 그 동률을 고려해서 거리를 정렬시켰을 때 k번째 해당하는 거리를 의미함.
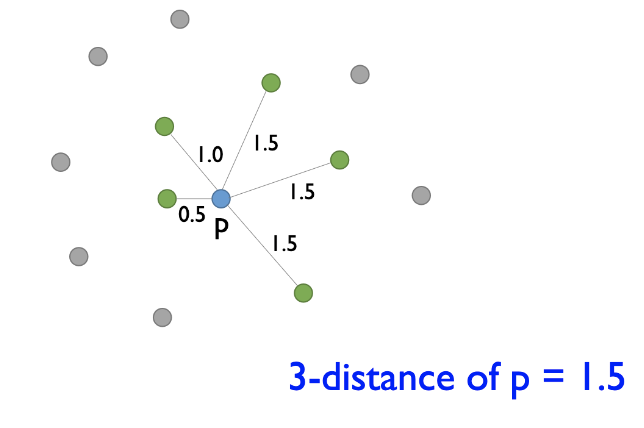
0.5 (1)
1.0 (2)
1.5 (3) 📌
1.5 (4)
1.5 (5)
- 5개 >= k(3)
- 2개 < k(3)
2. k-distance neighborhood of an object p
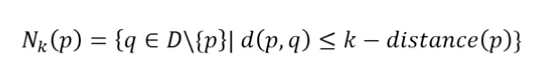
- 객체들의 집합에 대한 정의
- : 현재 데이터셋에서 를 제외한 집합 &
- 각 데이터 포인트에 대해 최근접 이웃을 찾기 위해 모든 데이터 포인트 간의 거리를 계산함.
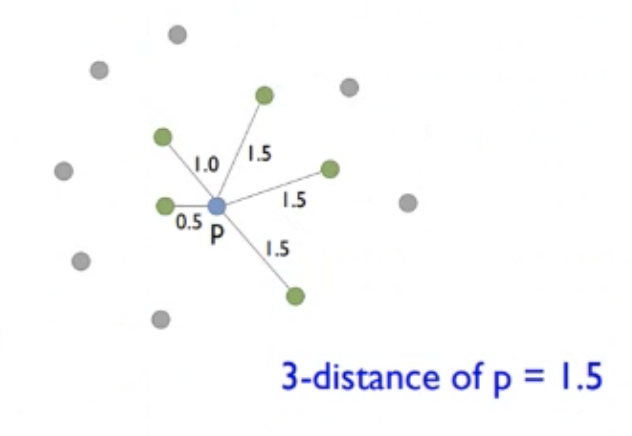
- p의 3-distance는 3번째로 가까운 이웃과의 거리인 1.5임.
조건1 <= : 5개 >= k:3 ⭕️
조건2 < : 2개 < k:3 ⭕️
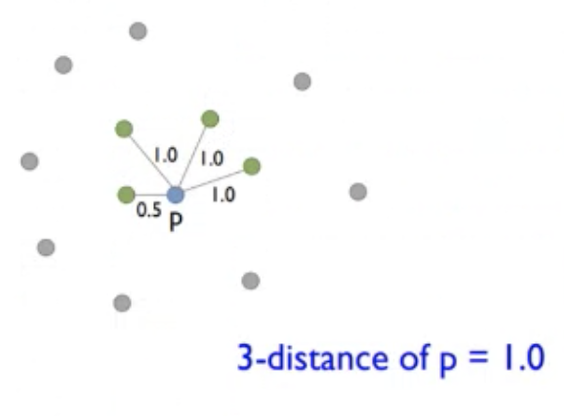
- p의 3-distance는 3번째로 가까운 이웃과의 거리인 1.0임.
조건1 <= : 4개 >= k:3 ⭕️
조건2 < : 1개 < k:3 ⭕️
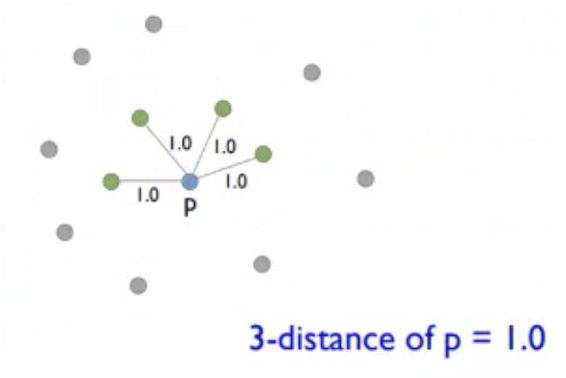
- p의 3-distance는 3번째로 가까운 이웃과의 거리인 1.0임.
조건1 <= : 4개 >= k:3 ⭕️
조건2 < : 0개 < k:3 ⭕️
3. reachability distance
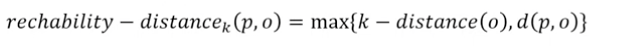
- 도달 가능거리라는 의미임.
- 여기서 에서 가 아니라 라는 점이 매우 중요함.
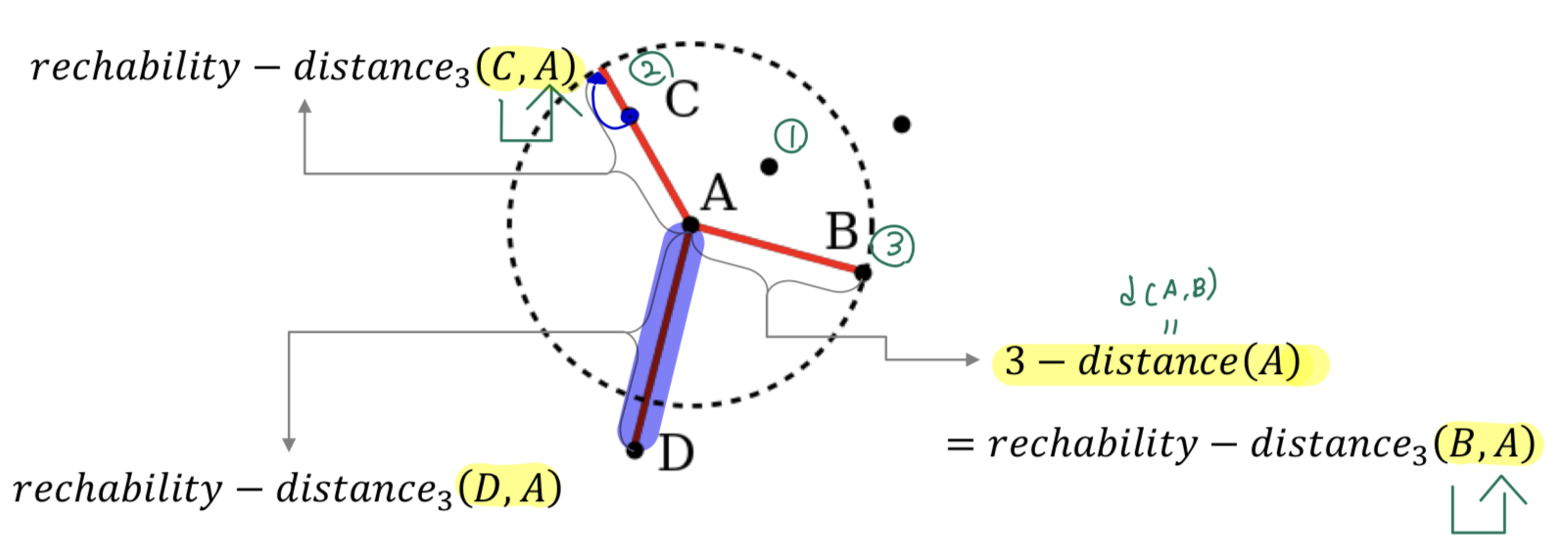
- 데이터 포인트 와 간의 reachability distance는 와 사이의 거리와 의 k-번째 최근접 이웃까지의 거리 중 더 큰 값임.
📌 이는 가 의 밀도가 높은 지역에 있을 때 그 거리를 과대 평가하는 것을 방지하기 위한 것임.
4. local reachability density of an object p (LRD)
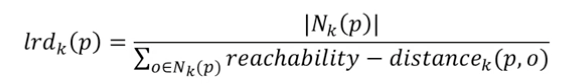
- 각 데이터 포인트의 LRD는 해당 데이터 포인트와 그의 k-최근접 이웃들 간의 평균 Reachability Distance의 역수임.
- 는 동률 발생 시 보정하는 역할임.

- black:
- blue:
- k = 5
- 밀도가 높은 지역 한 가운데에 p가 존재한다고 하면, 에 분모가 작기 때문에 값 자체는 커지게 됨.
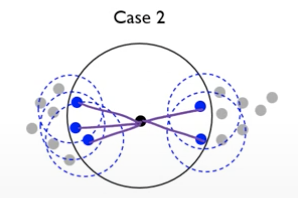
- 밀도가 높은 지역에 sparse한 지역에 P가 존재한다고 하면, 분모가 커지기 때문에 역수를 취한 값은 상대적으로 작아지게 됨.
5. local outlier factor of an object p
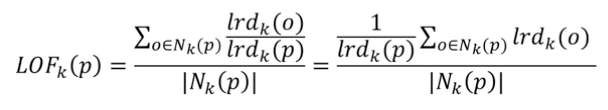
- 데이터 포인트의 LOF는 해당 데이터 포인트의 이웃들의 LRD의 평균값과 해당 데이터 포인트의 LRD와의 비율임.
- LOF값이 1보다 크면 해당 데이터 포인트의 밀도가 그의 이웃들보다 낮다는 것을 나타냄.
📌 LOF 값이 큰 데이터 포인트는 이상치로 간주될 가능성 up
- 분모
: p의 k-distance neighborhood의 속하는 객체의 수
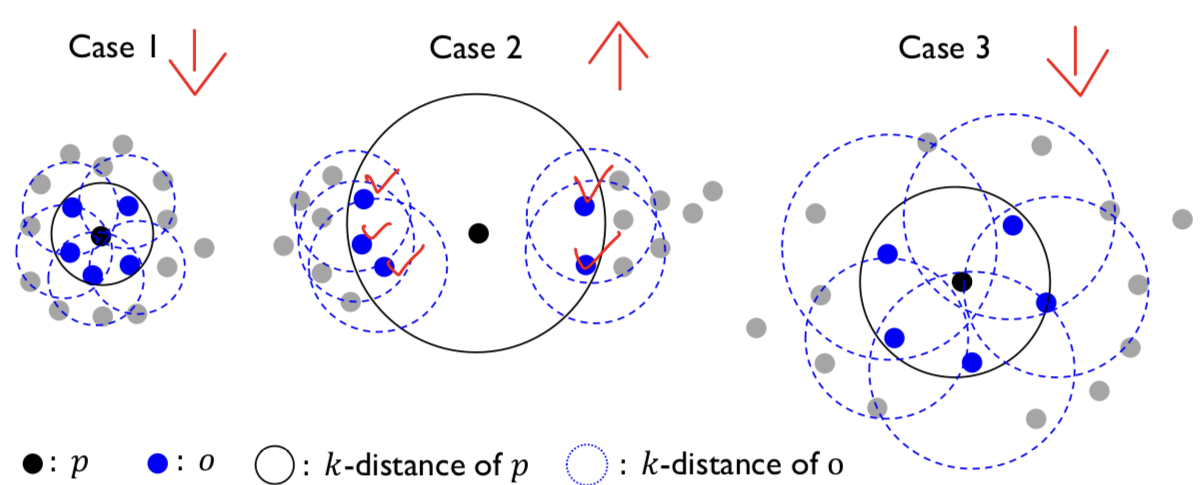
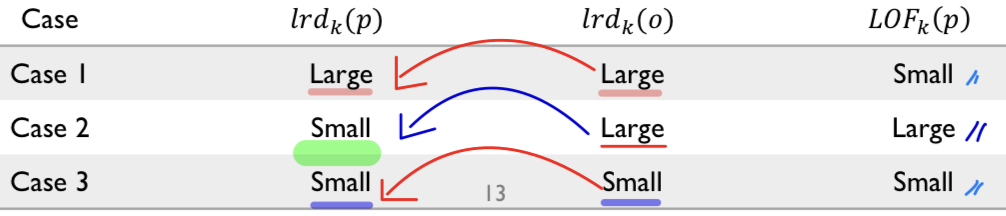
- 밀도가 높은 영역이나 밀도가 낮은 영역의 가운데 있는 객체에 대해서는 LOF score ⬇️
- 밀도가 높은 영역 사이에 낮은 밀도를 가진 객체에 대해서는 LOF score ⬆️
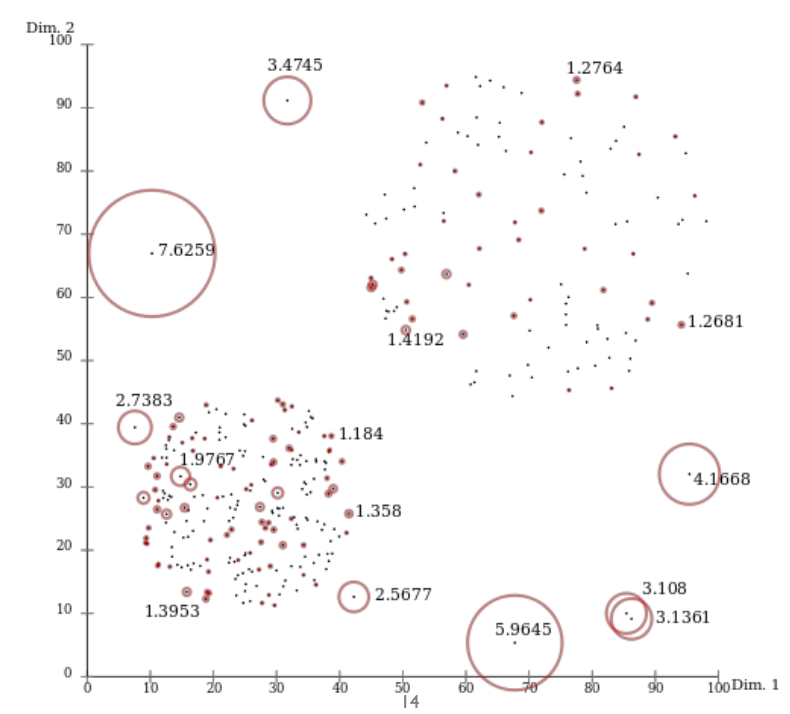
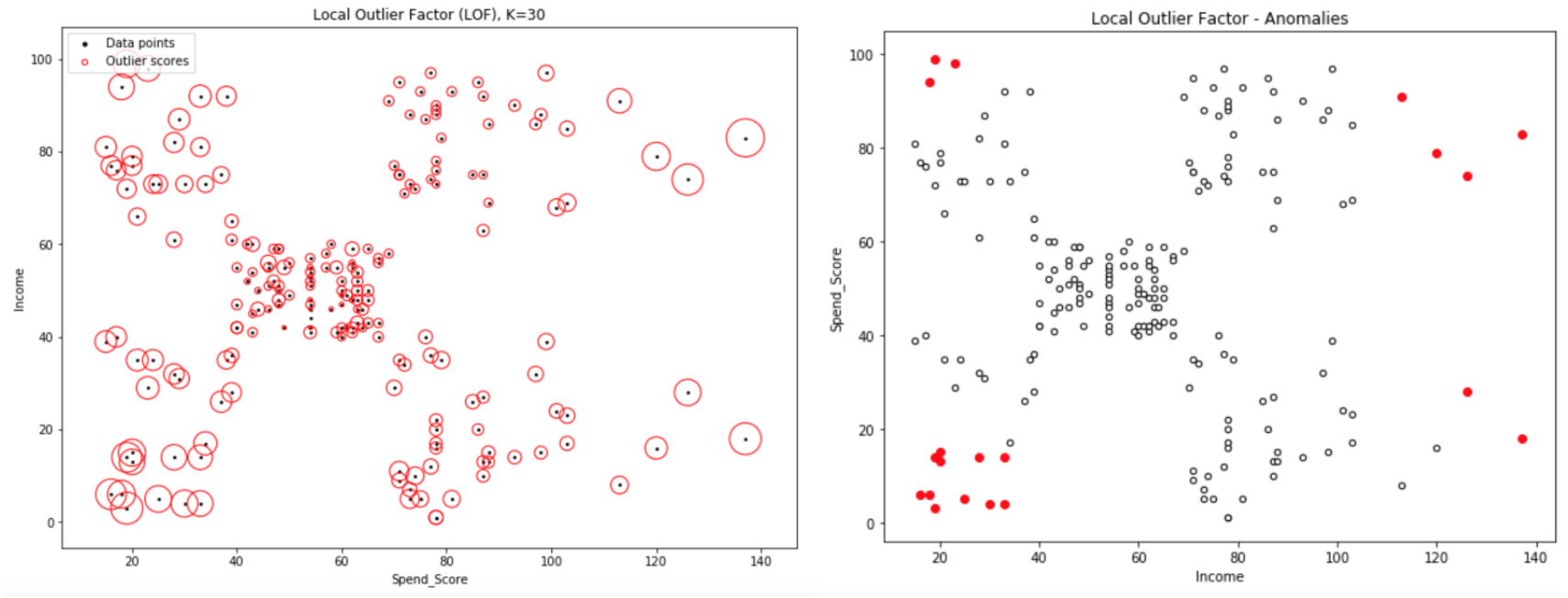
- 위의 그림은 LOF score를 확인할 수 있음.
📌 개별적인 포인트들에 대해서 local outlier score를 직접 하나하나씩 계산하는 것
- 주어진 데이터를 가지고 단순히 밀도를 추정하는 상황임.
🎯 Summary
[주요 아이디어]
(1) LOF는 데이터 포인트의 지역적 밀도를 이용해 이상치 탐지를 함.
(2) 이상치는 일반적으로 낮은 지역적 밀도를 갖고 이를 통해 일반 데이터 포인트와 구별함.
- LOF는 단일 논문이지만 많이 인용된 논문이여서 꼭 논문을 읽어봐야겠음.
- 현재까지도 다양한 이상치 탐지 분야에서 LOF 방법론을 사용하고 있으니 어렵더라도 복습을 계속 해야겠음.
- 강의자료와 유튜브를 무료로 볼 수 있게 한 DSBA 연구실에 감사의 인사를 전합니다.
📚 References
- Youtube
- https://www.youtube.com/watch?v=ODNAyt1h6Eg&list=PLetSlH8YjIfWMdw9AuLR5ybkVvGcoG2EW&index=19, DSBA 연구실 유튜브
- 강의 자료
