[자료구조] 스택(Stack)

9e0na·2023년 4월 19일
data structurepython
1

[자료구조]

목록 보기
5/7
post-custom-banner

주제: 파이썬에서 스택 구현하기

파이썬과 함께하는 자료구조의 이해[개정판] pp.88-97 참고해서 내용 작성하였습니다.
파이썬으로 배우는 자료구조 핵심 원리 pp.64-67 참고해서 내용 작성하였습니다.

1. 스택(Stack)

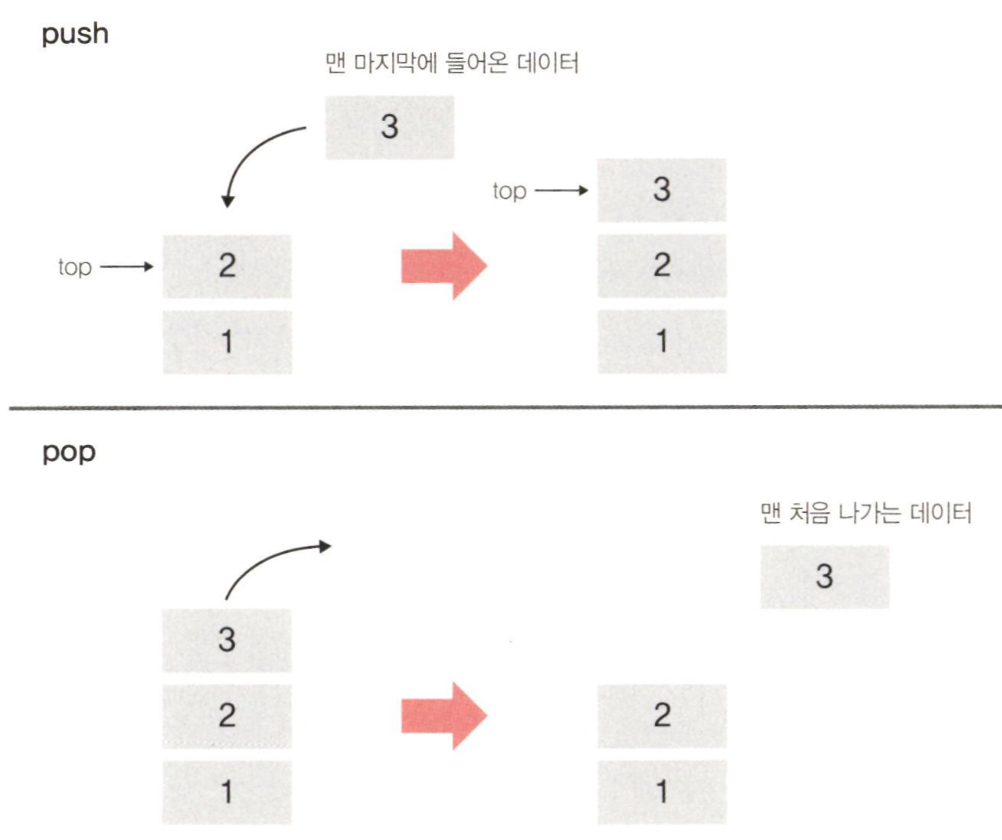
정의
: 한 쪽 끝에서만 item(항목)을 삭제하거나 새로운 item을 저장하는 자료구조를 의미한다.
접시 쌓기를 떠올리면 쉽다. 데이터가 들어오면 차곡차곡 쌓이고 나갈 때는 맨 위에 있는 데이터부터 나가게 된다.

  • 특징
    -push : 새 item을 저장(삽입)하는 연산

    -pop : op item을 삭제하는 연산

    -peek: 스택의 맨 위에 있는 데이터를 반환만 하는 연산

    -후입선출(Last-In First-Out, LIFO): 원칙 하에 Item의 삽입과 삭제 수행

  • 스택의 용도는?
    -되돌리기
    -함수호출
    -괄호 검사
    -계산기: 후위 표기식 계산, 중위 표기식의 후위 표기식 변환
    -미로탐색

1.1 스택의 구현

  • 데이터
    -top: 스택 항목을 저장하는 파이썬 리스트
    -항목의 개수는 len(top)으로 구할 수 있다.

  • 연산
    : isEmpty() , push() , pop() , peek() , display()

  • 항목 삽입 / 삭제 위치
    : 리스트의 맨 뒤가 유리하다. 앞에서 삭제가 이루어지면 많은 항목들의 이동이 필요하기 때문에 비효율적이다. 반면 뒤에서 삭제하면 바로 추가하면 되기 때문에 효율적이다.

1.2 코드 구현

1. 리스트로 구현한 스택

🤜 입력

def push(item):    # 삽입 연산
    stack.append(item)  # push() = append() 리스트의 맨 뒤에 item 추가

def peek():     # top 항목 접근
    if len(stack) != 0:
        return stack[-1]   # top항목:  리스트의 맨 뒤 항목 리턴
    
def pop():    # 삭제 연산
    if len(stack) != 0:
        item = stack.pop(-1)   # pop(): 리스트의 맨 뒤에 있는 항목 제거
        return item
stack = []  
push('apple')
push('orange')
push('cherry')
print('사과, 오렌지, 체리 push 후:\t', end='')
print(stack, '\t<- top')
print('top 항목: ', end='')
print(peek())
push('pear')
print('배push 후:\t\t', end='')
print(stack, 't<- top')
pop()
push('grape')
print('pop(), 포도push 후:\t', end='')
print(stack, 't<- top')

💻 출력

사과, 오렌지, 체리 push 후:	['apple', 'orange', 'cherry'] 	<- top
top 항목: cherry
배push 후:		['apple', 'orange', 'cherry', 'pear'] t<- top
pop(), 포도push 후:	['apple', 'orange', 'cherry', 'grape'] t<- top

수행시간

  • 파이썬의 리스트로 구현한 스택의 push와 pop 연산은 각각 O(1) 시간이 소요된다.
  • 파이썬의 리스트는 크기가 동적으로 확대 또는 축소된다. 이러한 크기 조절은 사용자도 모르게 수용되기 때문에 스택(리스트)의 모든 항목들을 새 리스트로 복사해야 한다. 그렇기 때문에 O(N) 시간이 소요된다.

2. 단순연결리스트로 구현한 스택

🤜 입력

class Node:
    def __init__(self, item, link):  
        self.item = item   # 노드 생성자 항목과
        self.next = link   # 다음 노드 레퍼런스
    
def push(item):
    global top  # 전역변수
    global size # 전역변수
    top = Node(item, top)  # 새 노드 객체를 생성하여 연결리스트의 첫 노드로 삽입
    size += 1
    
def peek():
    if size != 0:
        return top.item  # top 항목만 리턴 
        
def pop():
    global top  # 전역변수 
    global size  # 전역변수
    if size != 0:
        top_item = top.item
        top = top.next  # 연결리스트에서 top이 참조하던 노드를 분리시킨다.
        size -= 1
        return top_item  # 제거된 top 항목 리턴한다.
        
def print_stack():
    print('top ->\t', end='')
    p = top
    while p:
        if p.next != None:
            print(p.item, '-> ', end='')
        else:
            print(p.item, end='')
        p = p.next
    print()
        
top = None  # 초기화
size = 0  # 초기화
push('apple')
push('orange')
push('cherry')
print('사과, 오렌지, 체리 push 후:\t', end='')
print_stack()
print('top 항목: ', end='')
print(peek())
push('peer')
print('배 push 후: \t\t', end='')
print_stack()
pop()
push('grape')
print('pop(), 포도 push 후:\t', end='')
print_stack()

💻 출력

사과, 오렌지, 체리 push 후:	top ->	cherry -> orange -> apple
top 항목: cherry
배 push 후: 		top ->	peer -> cherry -> orange -> apple
pop(), 포도 push 후:	top ->	grape -> cherry -> orange -> apple

수행시간

  • push와 pop 연산은 각각 O(1) 시간이 소요된다.
    왜냐하면 연결리스트의 맨 앞 부분에서 노드를 삽입하거나 삭제하기 때문이다.

2. 스택의 응용

  • 컴파일러의 괄호 짝 맞추기
  • 회문(Palindrome) 검사하기
  • 후위표기법 수식 계산하기

2.1 괄호 검사

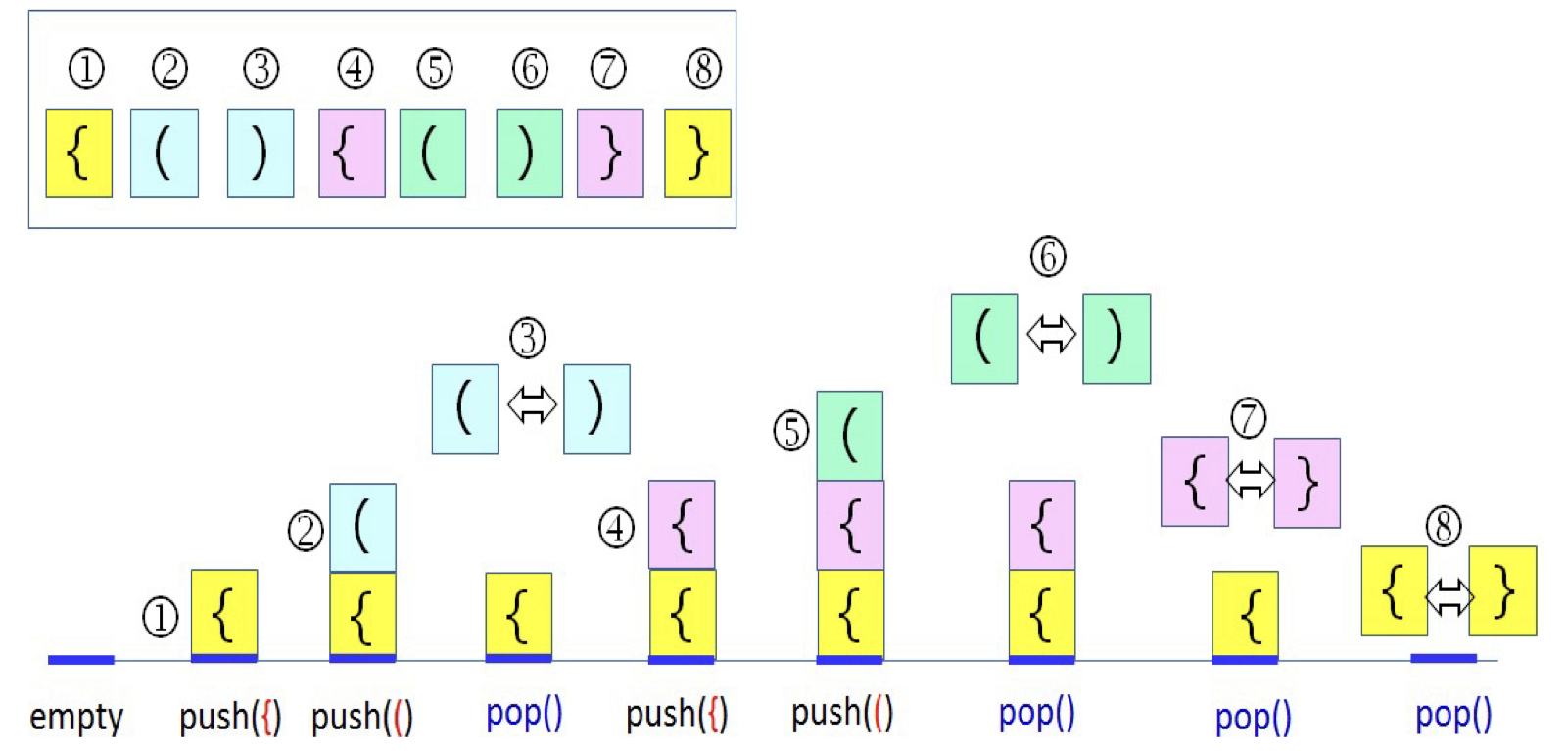
핵심 아이디어
: 왼쪽 괄호는 스택에 push, 오른쪽 괄호를 읽으면 pop 수행한다.

  • 조건
    -조건1: 왼쪽 괄호의 개수와 오른쪽 괄호의 개수가 같아야 한다.
    -조건2: 왼쪽 괄호는 오른쪽 괄호보다 먼저 나와야 한다.
    -조건3: 괄호 사이에는 포함 관계만 존재한다.

1. 코드 구현

🤜 입력

# 스택의 구현 (클래스 버전)
class Stack:
    def __init__(self):
        self.top = []
        
    def isEmpty(self): return len(self.top) == 0
    def size(self): return len(self.top)
    def clear(self): self.top = []
        
    def push(self,item):
        self.top.append(item)
    
    def pop(self):
        if not self.isEmpty():
            return self.top.pop(-1)
    
    def peek(self):
        if not self.isEmpty():
            return self.top[-1]
        
# 괄호 검사 알고리즘
def checkBrackets(statement):
    stack = Stack()
    for ch in statement:
        if ch in ('{', '[', '('):
            stack.push(ch)
        elif ch in ('}', ']', ')'):
            if stack.isEmpty():
                return False  # 조건 2 위반
            else:
                left = stack.pop()
                if (ch == '}' and left != '{') or \
                   (ch == ']' and left != '[') or \
                   (ch == ')' and left != '('):
                    return False  # 조건 3 위반
                
    return stack.isEmpty()  # False이면 조건 1 위반

2 결과

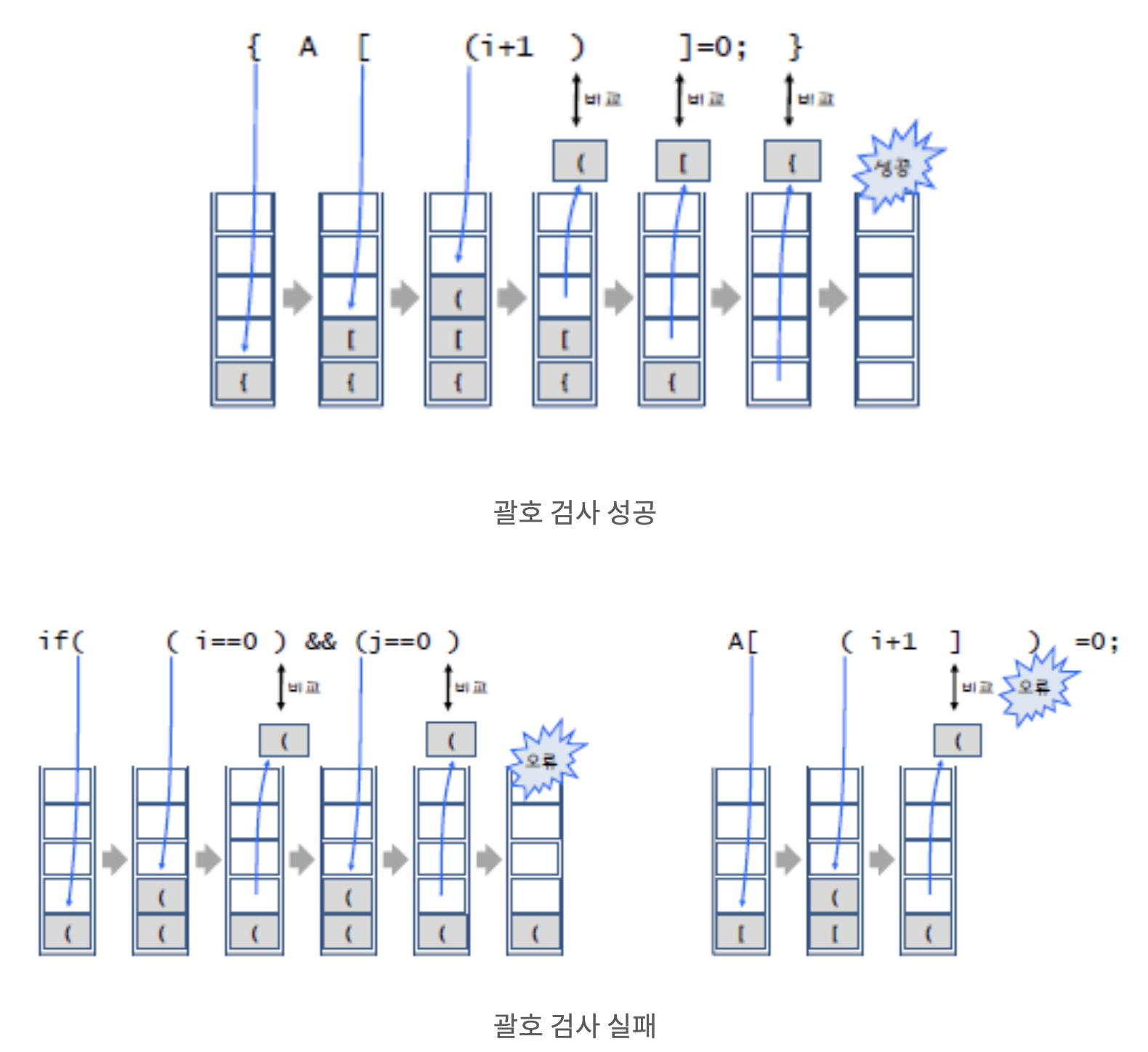
  • 위의 그림은 괄호검사 예시다.

    출처: 티스토리, '[자료구조] 스택(stack)의 응용1: 괄호검사-컴도리돌이', https://comdolidol-i.tistory.com/45 (검색일: 2023.04.19.).

🤜 입력

str = ("{A[(i+1)]=0;}", "if((i=0)&&(j==0)", "A[(i+1])=0;")
for s in str:
    m = checkBrackets(s)
    print(s, "-->", m)

💻 출력

{A[(i+1)]=0;} --> True
if((i=0)&&(j==0) --> False
A[(i+1])=0; --> False

2.2 회문 검사

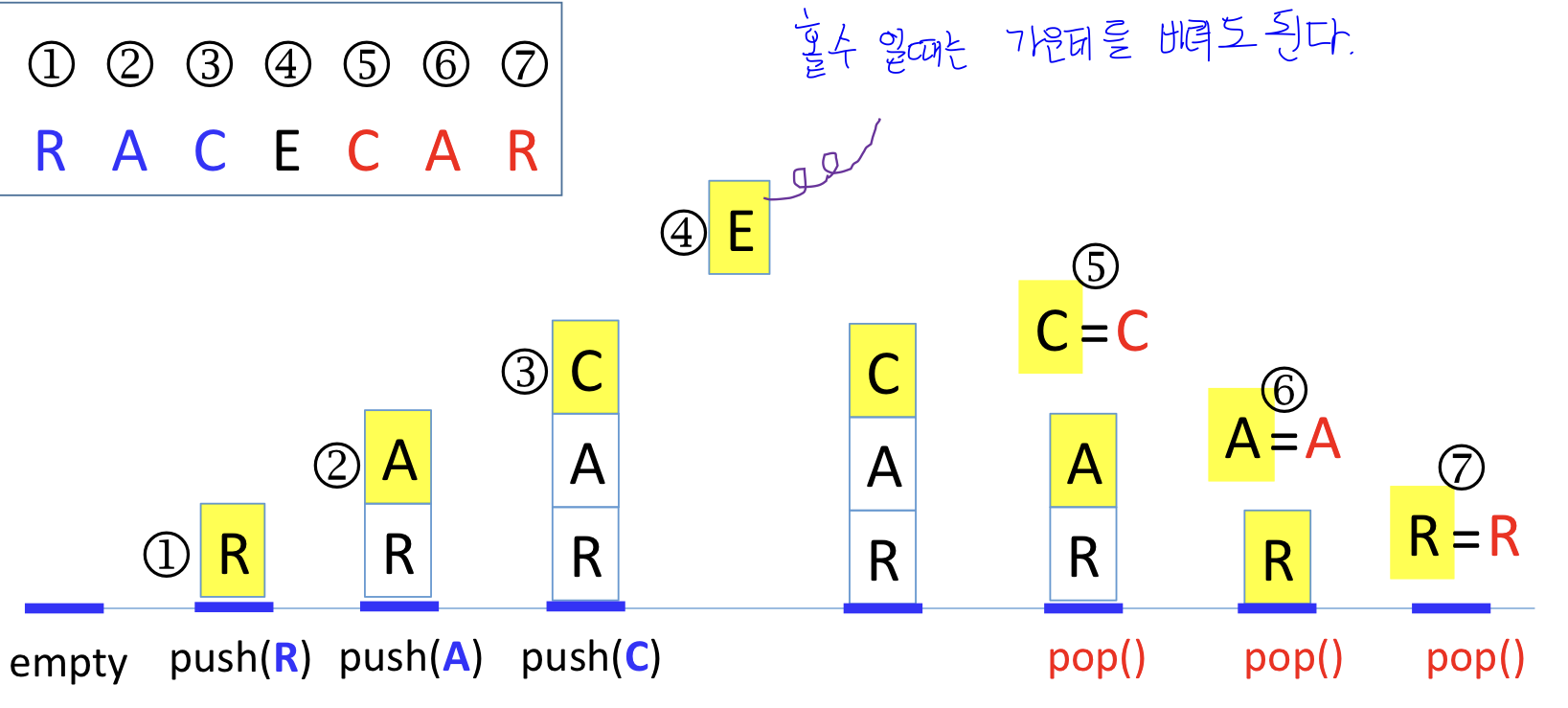
회문(Palindrome)이란?
: 앞으로부터 읽으나 뒤로부터 읽으나 동일한 스트링을 의미한다.

핵심 아이디어는?
: 전반부의 문자들을 스택에 push한 후, 후반부의 각 문자를 차례로 pop한 문자와 비교

1. 프로세스

  • 1) 주어진 스트링의 앞부분 반을 차례대로 읽어 스택에 push한다.
  • 2) 문자열의 길이가 짝수이면, 뒷부분의 문자 1개를 읽을 때마다 pop하여 읽어들인 문자와 pop된 문자를 비교하는 과정을 반복 수행한다.
  • 3) 마지막 비교까지 두 문자가 동일 & 스택이 empty가 되면, 입력 문자열은 회문이 된다.
  • 4) 문자열의 길이가 홀수이면, 주어진 스트링의 앞부분 반을 차례로 읽어 스택에 push한 후, 중간 문자를 읽고 버린다. 이후 짝수 경우와 동일하게 비교 수행을 한다.

3. 수식의 표기법 (후위표기법)

  • 중위표기법
    : 프로그래밍을 작성할 때 수식에서 +.-.*,/와 같은 이항연산자는 2개의 피연산자들 사이에 위치한다.

  • 후위표기법
    :괄호 없이 중위표기법 수식을 표현할 수 있는 수식이고, 보통 중위표기법 수식을 후위표기법으로 바꾼다.

  • 전위표기법
    : 연산자를 피연산자들 앞에 두는 표기법을 말한다.

    중위표기법후위표기법전위표기법
    A+BAB++AB
    A+B-CAB+C--+ABC
    A+B*C-DABC*+D--+A*BCD
    (A+B)/(C-D)AB+CD-//+AB-CD

3.1 후위표기법 수식 계산

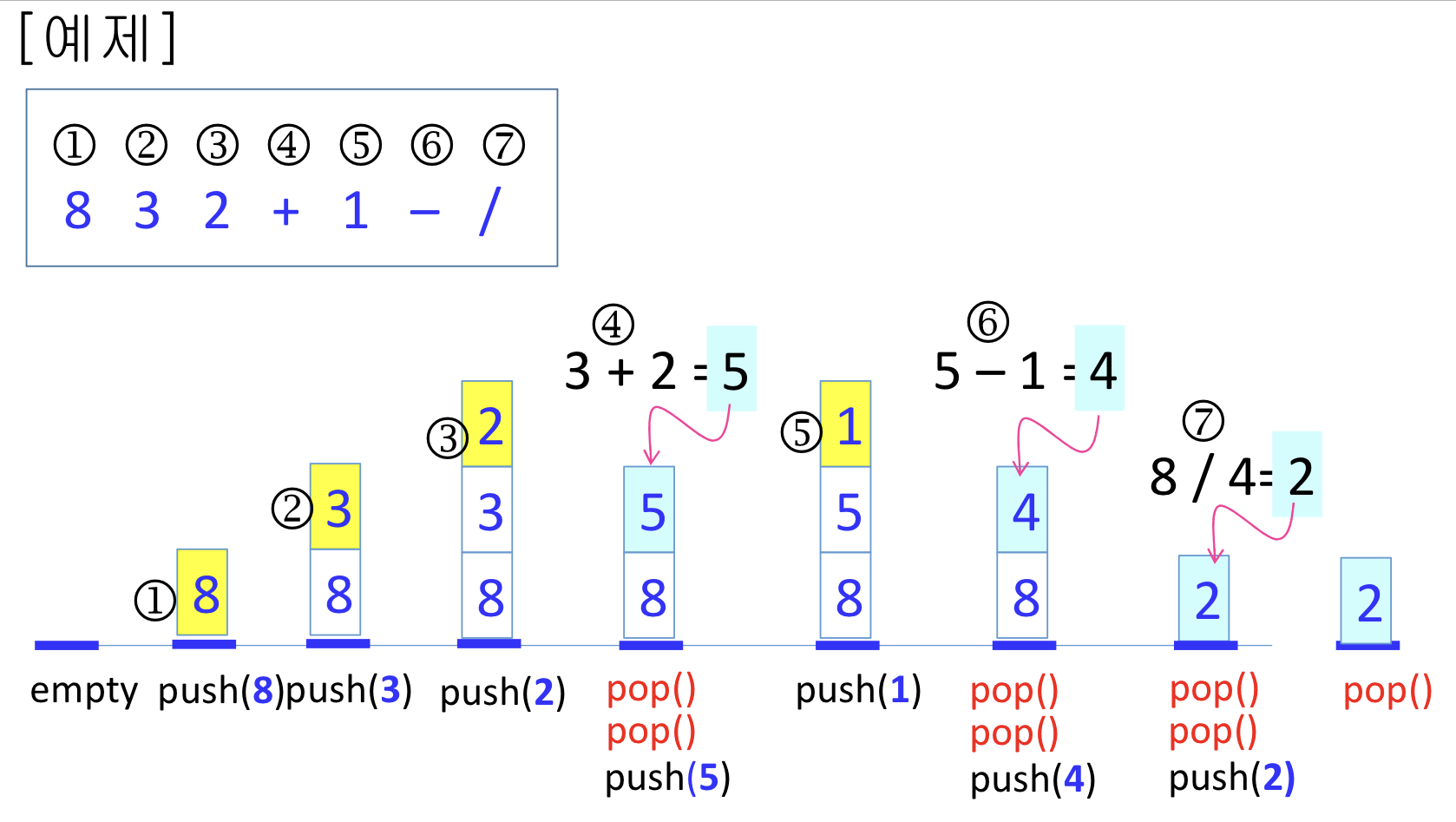
핵심 아이디어는?
: 피연산자는 스택에 push하고, 연산자는 2회 pop하여 계산한 후 push한다.

  • 4번에서 '+'는 연산자이므로, pop을 2회 수행하기 때문에 3+2=5를 push한다.
  • 6번에서 '-'는 연산자이므로, 위의 똑같이 pop을 2회 수행하고 5-1=4를 push한다.
  • 7번도 마찬가지로 위와 같이 pop을 하기 때문에 8/4 = 2를 push한다.

3.2 중위표기법 수식을 후위표기법으로 변환

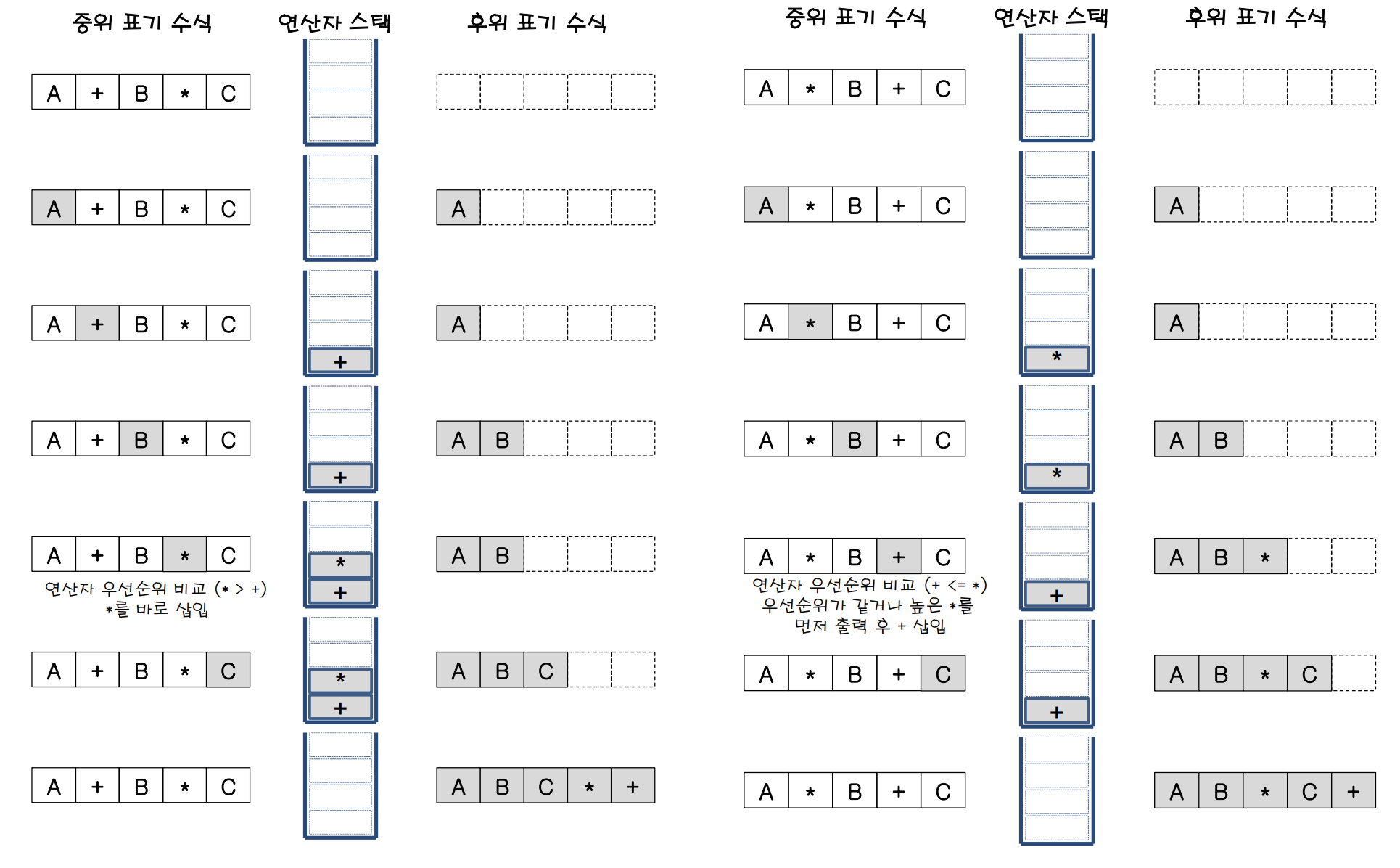
핵심 아이디어는?
: 왼쪽 괄호나 연산자는 스택에 push하고, 피연산자는 출력한다.

  • 입력을 좌에서 우로 문자를 1개씩 읽는다. 읽은 문자가
  1. 피연산이면, 읽은 문자를 그대로 출력한다.
  2. 연산자이면, 스택에 저장했다가 스택보다 우선 순위가 낮은 연산자가 나오면 그때 출력한다.
  3. 왼쪽 괄호는 우선순위가 가장 낮은 연산자로 취급한다. (괄호 연산자는 연산자 우선순위가 제일 낮다.)
  4. 오른쪽 괄호이면, 스택에서 왼쪽 괄호위에 쌓여 있는 모든 연산자를 출력한다.
  5. 입력을 모두 읽었으면, 스택이 empty될 때까지 pop 출력한다.

  • 첫번째 중위 표기 수식인 A+B*C를 보면,
    1) 피연산자 A는 출력
    2) +는 스택에 저장
    3) 피연산자 B는 출력
    4) *는 스택에 저장 -> (* > +이므로 * 연산자 우선 순위가 높기 때문에 그대로 스택에 저장)
    5) 피연산자 C는 출력
    6) pop하면, ABC*+ 출력

  • 두번째 중위 표기 수식인 A*B+C를 보면,
    1) 피연산자 A는 출력
    2) *는 스택에 저장
    3) 피연산자 B는 출력
    4) *는 +보다 연산자 우선 순위가 같거나 높기 때문에 스택에서 빠져나와 출력. (* 출력, + 스택에 저장)
    5) 피연산자 C는 출력
    6) pop하면, AB*C+ 출력

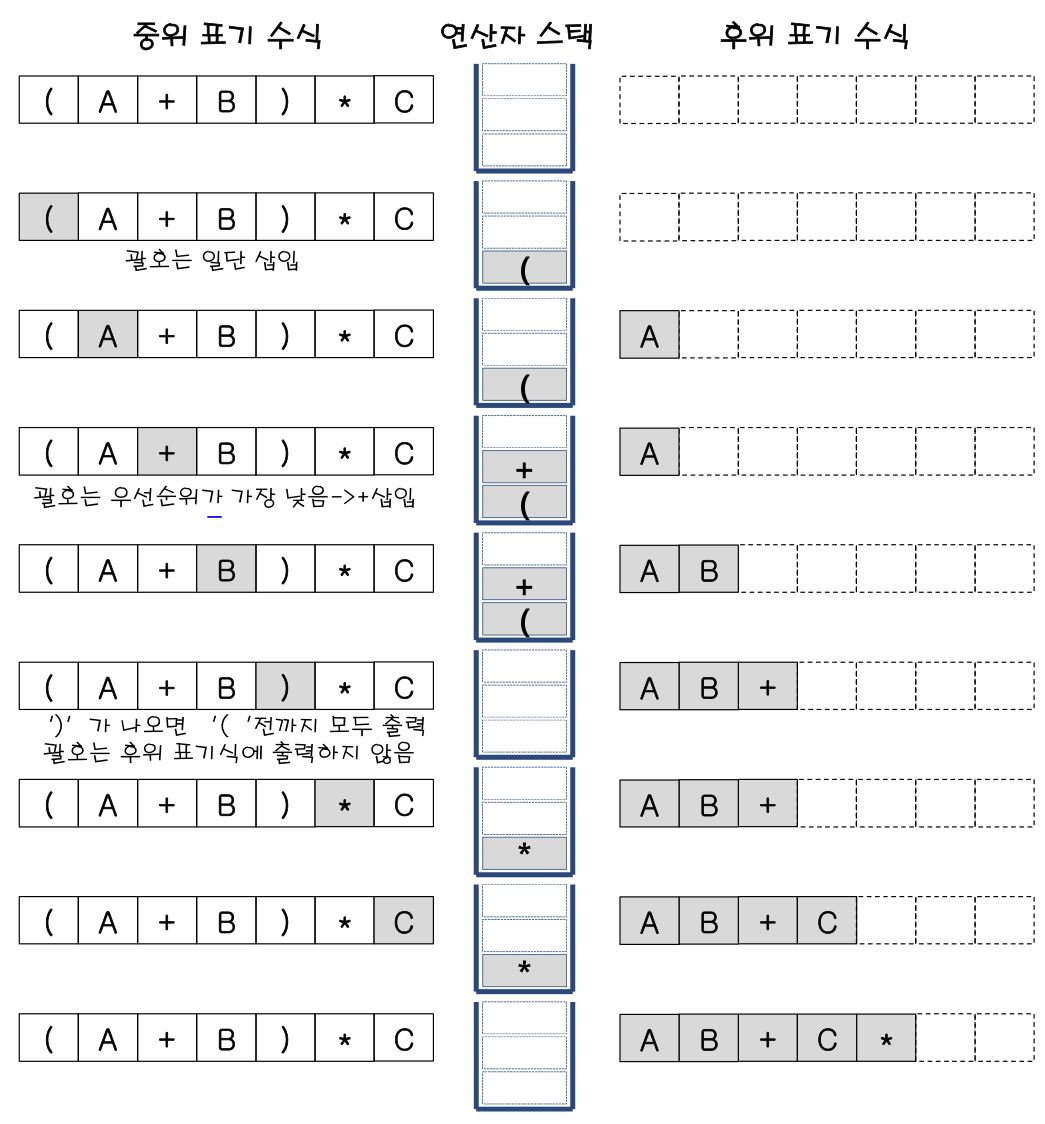
  • 세번째 중위 표기 수식인 (A+B)*C를 보면,
    1) '(' 괄호는 스택에 저장
    2) 피연산자 A는 출력
    3) +는 스택에 저장 (괄호는 우선순위가 제일 낮기 때문에..)
    4) 피연산자 B는 출력
    5) ')' 괄호가 나오면 '('전까지 모두 출력 (괄호는 후위 표기식에 출력하지 않는다. / +출력)
    6) * 는 스택에 저장
    7) 피연산자 C는 출력
    8) pop하면, AB+C* 출력

🎯 Summary

중위표기식을 후위표기법으로 변환하는 과정에서 스택의 성질을 확실히 알 수 있었다. 이때는 연산자를 스택한다. 하지만 그냥 후위표기법을 계산할 때에는 피연산자를 스택한다. 이 부분이 살짝 헷갈렸다. 그리고 단일연결리스트로 스택을 구현할 때, 그 전에 배운 단일연결리스트의 중요성을 알 수 있었다. 그 전에 공부했을 때는 복잡해보였지만, 막상 공부해보니 별거 아니였다.

어려운 코드가 나오더라도 하나하나 코드를 뜯어보면서 내 것으로 만드는 습관을 길들이는 것이 매우 중요한 것 같다.

📚 References

  • 양성봉(2022),'파이썬과 함께하는 자료구조의 이해[개정판]', 생능출판, pp.88-97.
  • 양태환(2021),'파이썬으로 배우는 자료구조 핵심 원리', 길벗, pp.64-67.
  • 괄호 검사 예시 그림: 티스토리, '[자료구조] 스택(stack)의 응용1: 괄호검사-컴도리돌이', https://comdolidol-i.tistory.com/45 (검색일: 2023.04.19.).
profile
9e0na
데이터사이언티스트가 되기 위해 [a-zA-Z]까지 정리하는 거나입니다 😊
이전 포스트

[자료구조] 연결리스트_이중 & 원형 연결리스트

다음 포스트

[자료구조] 큐(QUEUE)

post-custom-banner

0개의 댓글