주제: 파이썬에서 큐 구현하기
파이썬과 함께하는 자료구조의 이해[개정판] pp.97-101 참고해서 내용 작성하였습니다.
파이썬으로 배우는 자료구조 핵심 원리 pp.67-74 참고해서 내용 작성하였습니다.
1. 큐(QUEUE)
정의
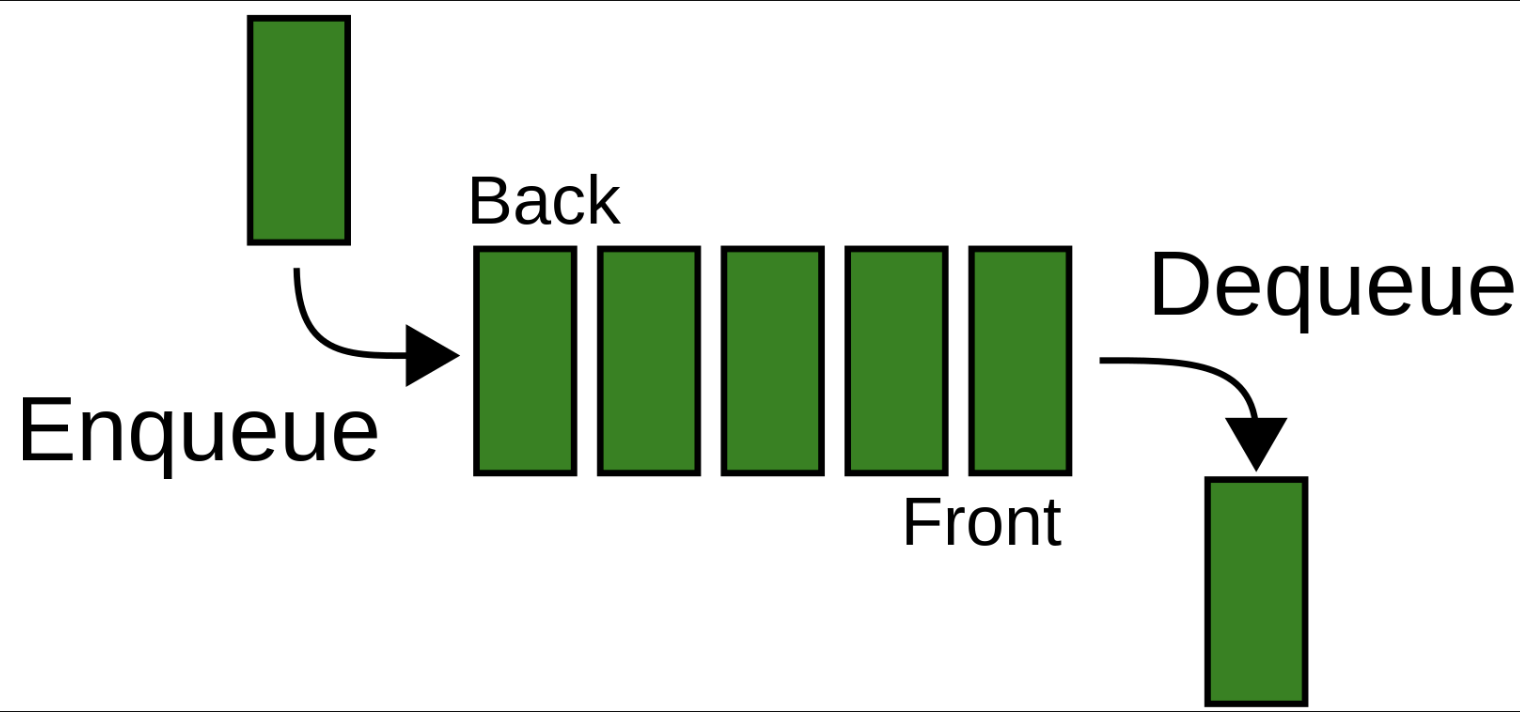
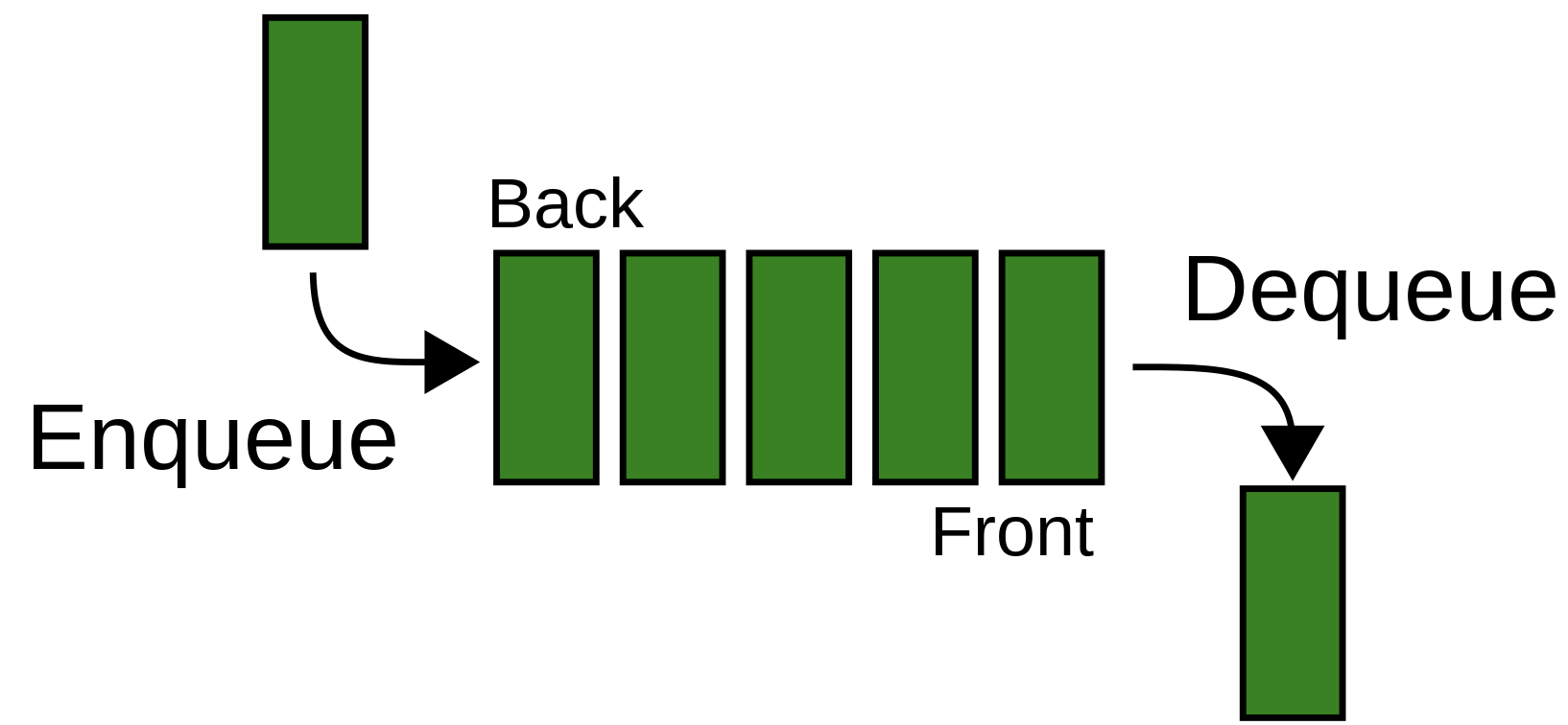
: 큐는 삽입과 삭제가 양 끝에서 각각 수행되는 자료구조이다. 큐는 줄서기를 생각하면 된다.
- 특징
-선입선출 (First-In First Out: FIFO)의 자료구조이다.
-일상생활의 관공서, 은행, 우체국, 병원 등에서 번호표를 이용한 줄서기 등을 예시로 들 수 있다.
-삽입은 큐의 후단에서, 삭제는 전단에서 이루어진다.
- 큐 ADT
-Queue():
비어 있는 새로운 큐를 만든다
-isEmpty():
큐가 비어있으면 True 아니면 False 반환
-enqueue(x)
: 항목 x를 큐의 맨 뒤에 추가한다.
-dequeue(x)
:큐의 맨 앞에 있는 항목을 꺼내 반환한다.
-peek()
: 큐의 맨 앞에 있는 항목을 삭제하지 않고 반환한다.
-size()
: 큐의 모든 항목들의 개수를 반환한다.
- 큐의 실생활
-프린터와 컴퓨터 사이의 인쇄 작업 큐 (버퍼링)
-실시간 비디오 스트리밍에서의 버퍼링
-시뮬레이션의 대기열(공항의 비행기들, 은행에서의 대기열)
-통신에서의 데이터 패킷들의 모델링에 이용
- 큐의 실생활
1.1 큐의 구현
선형큐는 비효율적이다.
- enqueue(item): 삽입 연산, 리스트의 맨 뒤에 items추가 -> O(1)
- dequeue: 삭제 연산 -> O(n) / 리스트의 맨 앞에서 항목을 삭제하면 그 항묵 이후의 모든 항목을 한 칸씩 앞으로 이동해야 하므로 매우 비효율적이다
1.2 코드 구현
1. 파이썬 리스트로 구현한 큐
🤜 입력
def add(item): # 삽입 연산
q.append(item) # 맨 뒤에 새 항목 삽입
def remove():
if len(q) != 0:
item = q.pop(0) # 맨 앞의 항목 삭제
return item
def print_q(): # 큐 출력
print('front -> ', end='')
for i in range(len(q)):
print('{!s:<8}'.format(q[i]), end='') # 맨 앞부터 항목들을 차례로 출력
print(' <- rear')
q=[]
add('apple')
add('orange')
add('cherry')
add('pear')
print('사과, 오렌지, 체리, 배 삽입 후: \t', end='')
print_q()
remove()
print('remove한 후:\t\t', end='')
print_q()
remove()
print('remove한 후:\t\t', end='')
print_q()
add('grape')
print('포도 삽입 후:\t\t', end='')
print_q()💻 출력
사과, 오렌지, 체리, 배 삽입 후: front -> apple orange cherry pear <- rear
remove한 후: front -> orange cherry pear <- rear
remove한 후: front -> cherry pear <- rear
포도 삽입 후: front -> cherry pear grape <- rear2. 원형 큐
정의
: 선형으로 이어져 있는 동적 배열을 마치 원형처럼 사용하는 방법을 의미한다.
메모리를 효율적으로 관리할 수 있다.
-
전단과 후단을 위한 2개의 변수가 존재한다
-front: 첫번째 요소 하나 앞의 인덱스
-rear: 마지막 요소의 인덱스 -
회전(시계방향)방법:
front <- (front+1) % MAX_QSIZE
rear <- (rear+1) % MAX_QSIZE2.1 원형 큐의 과정
1. 삽입, 삭제 과정
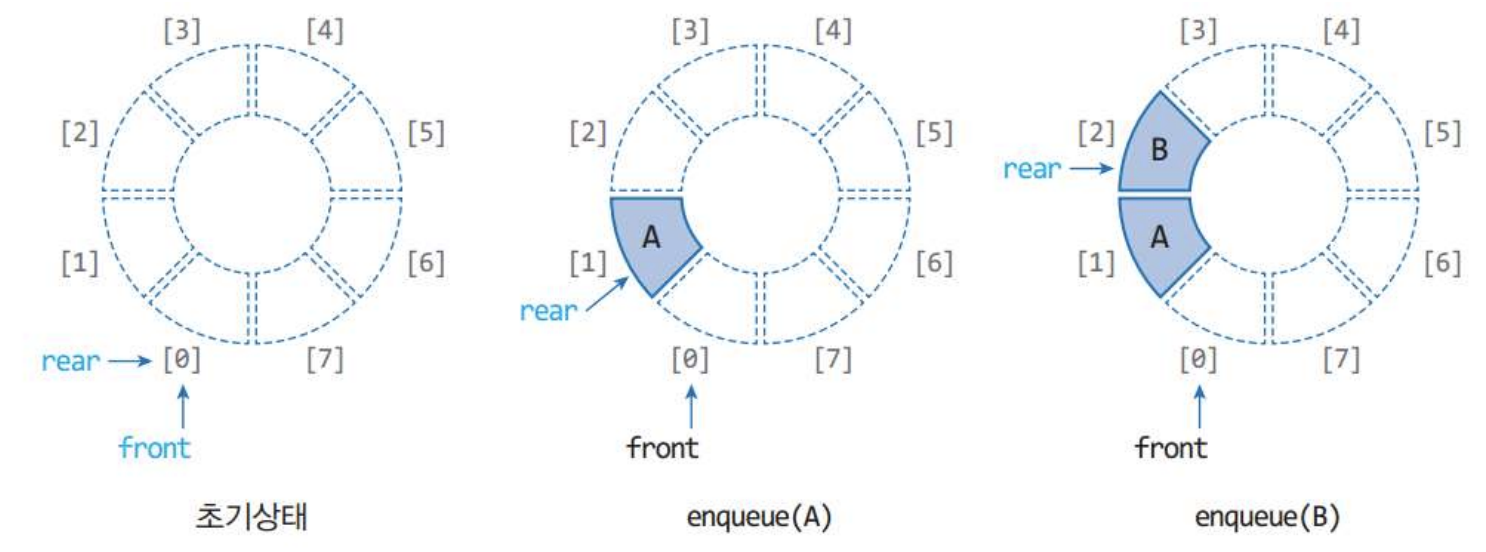
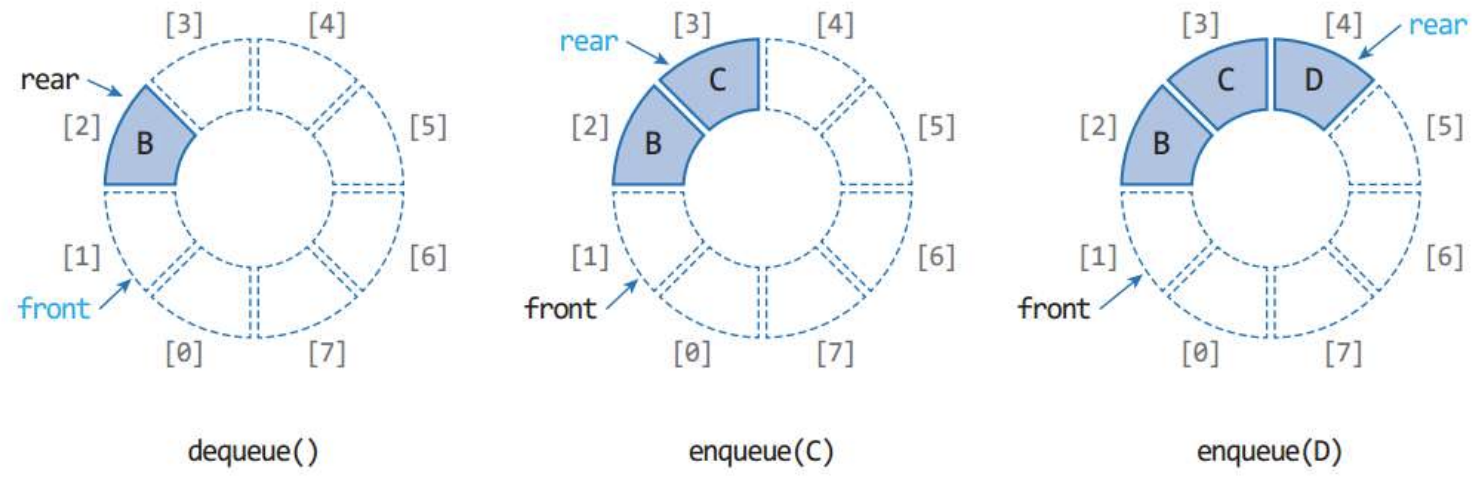
- dequeue 연산마다 모든 데이터를 한 번씩 이동시키는 문제점 -> front를 뒤로 한 번만 이동함
* 하지만 매번 dequeue 연산을 할 때마다 동작 배열이 앞부분이 하나씩 비게 되고 enqueue 연산은 계속되어 rear가 동적 배열의 맨 마지막에 도달했을 때는 데이터의 공간이 있음에도 불구하고 큐가 가득찼다고 판단하게 된다.
rear가 배열의 맨 마지막에 도달했을 때는 동적 배열의 맨 처음을 가리키게 하여 빈 공간에 데이터 추가를 한다.
2. 공백상태와 포화상태
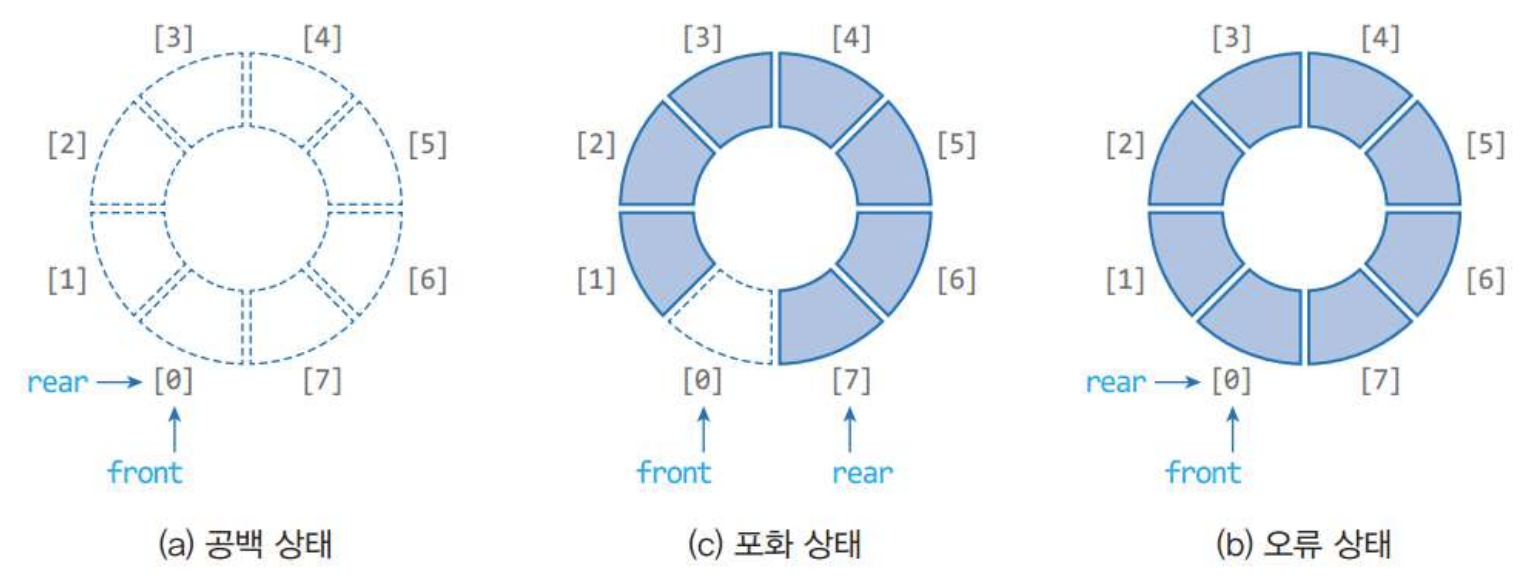
- 공백상태: front == rear
- 포화상태: front == (rear+1) % MAX_QSIZE
공백상태와 포화상태를 구별하는 방법은 하나의 공간을 항상 비워두는 것이다.
2.2 원형 큐의 구현
- 파이썬 리스트 사용
- 리스트의 크기가 미리 결정되어야 한다 -> 포화상태 있음
- MAX_QSIZE
- self.front, self.front, self.rear
- self.items = [NONE] * MAX_QSIZE
- def isEmpty(self): return self.front == self.rear # 공복상태
- def isFull(self): return self.front ==(self.rear+1)%MAX_QSIZE # 포화상태
- 삽입: rear+1
- 삭제: front+1
2.3 코드 구현
1 원형 큐 클래스
🤜 입력
MAX_QSIZE = 10 #원형크의 크기
class CircularQueue:
def __init__(self):
self.front = 0 #큐의 전단위치
self.rear = 0 #큐의 후단위치
self.items = [None] * MAX_QSIZE #항목 저장용 리스트
def isEmpty(self):
return self.front == self.rear #공백 상태
def isFull(self):
return self.front == (self.rear+1) % MAX_QSIZE
def enqueue(self,item):
if not self.isFull(): #포화 상태가 아니면
self.rear = (self.rear+1) % MAX_QSIZE #rear회전
self.items[self.rear] = item #rear위치에 item삽입
def dequeue(self):
if not self.isEmpty(): #공백 상태가 아니면
self.front = (self.front+1) % MAX_QSIZE #front회전
return self.items[self.front] #front위치 항목 반환
def peek(self):
if not self.isEmpty():
return self.items[(self.front+1)%MAX_QSIZE] #맨앞에 있는 항목 반환
def size(self): #인덱스 번호 계산
return (self.rear-self.front + MAX_QSIZE) % MAX_QSIZE
def display(self):
out = []
if self.front < self.rear: #한바퀴 안돌아간 상태
out = self.items[self.front+1:self.rear+1]
else: #한바퀴 돌아가 상태
out = self.items[self.front+1:MAX_QSIZE] + self.items[0:self.rear+1]
print('{f=%d,r=%d}=>'%(self.front,self.rear),out)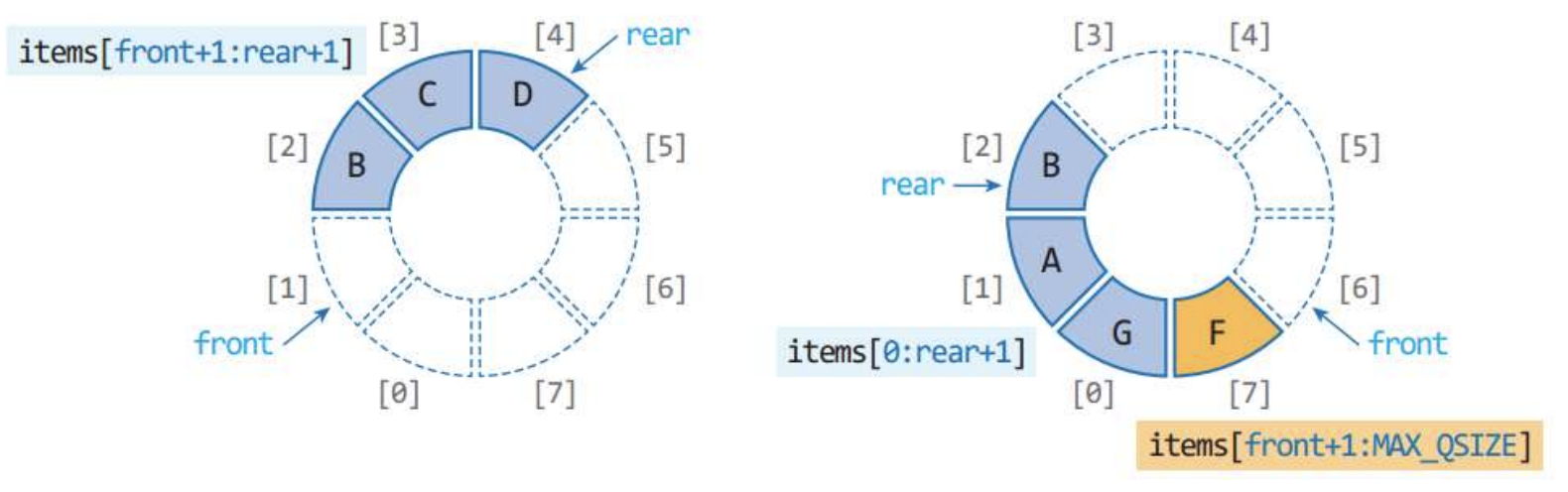
self.rear - self.front + MAX_QSIZE %MAX_QSIZE
: 음수가 나왔기 때문에 index번호 계산을 위와 같이 하였다.
🤜 사용예시
q = CircularQueue()
for i in range(8): q.enqueue(i) #0,1,...7삽입(f=0, r=8)
q.display()
for i in range(5): q.dequeue(); # 5번 삭제(f=5, r=8)
q.display()
for i in range(8,14): q.enqueue(i) # 8,9,...,13삽입(f=5,r=4)
q.display()💻 출력
{f=0,r=8}=> [0, 1, 2, 3, 4, 5, 6, 7]
{f=5,r=8}=> [5, 6, 7]
{f=5,r=4}=> [5, 6, 7, 8, 9, 10, 11, 12, 13]2 단순연결리스트로 구현한 큐
🤜 입력
class Node:
def __init__(self, item, n):
self.item = item
self.next = n
def add(item): # 삽입 연산
global size
global front # 전역변수
global rear # 빈 노드
new_node = Node(item, None) # 새 노드 객체를 생성
if size ==0:
front = new_node
else:
rear.next = new_node # 연결리스트의 맨 뒤에 삽입
rear = new_node #rear의 동작
size += 1
def remove(): # 삭제 연산
global size
global front
global rear
if size != 0:
fitem = front.item
front = front.next # 연결리스트에서 front가 참조하던 노드 분리시킴
size -= 1
if size == 0:
rear = None
return fitem # 제거된 맨 앞의 항목 리턴🤜 사용예시
def print_q(): # 큐 출력
p = front
print('frontL ', end='')
while p:
if p.next != None:
print(p.item, '-> ', end='')
else:
print(p.item, end='')
p = p.next
print(' :rear')
front = None # 초기화
rear = None
size = 0
add('apple')
add('orange')
add('cherry')
add('pear')
print('사과, 오렌지, 체리, 배 삽입 후: \t', end='')
print_q()
remove()
print('remove한 후:\t\t', end='')
print_q()
remove()
print('remove한 후:\t\t', end='')
print_q()
add('grape')
print('포도 삽입 후:\t\t', end='')
print_q()💻 출력
사과, 오렌지, 체리, 배 삽입 후: front: apple -> orange -> cherry -> pear :rear
remove한 후: front: orange -> cherry -> pear :rear
remove한 후: front: cherry -> pear :rear
포도 삽입 후: front: cherry -> pear -> grape :rear3. 원형연결리스트의 응용: 연결된 큐
1) 단순연결리스트로 구현한 큐
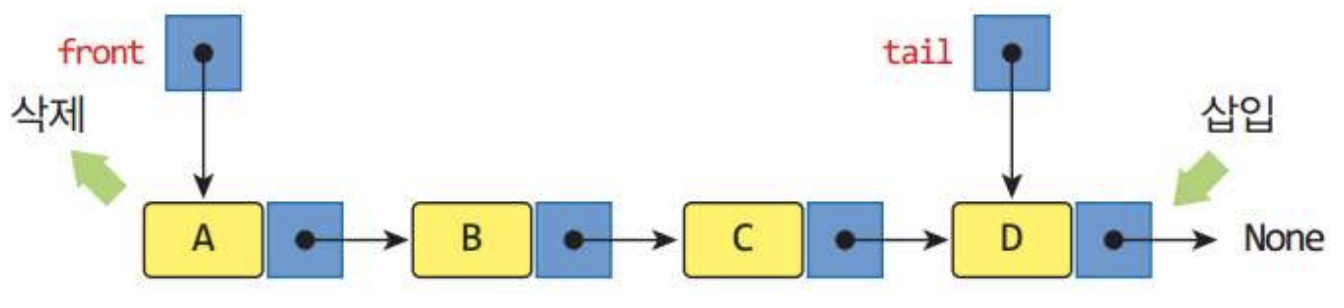
2) 원형연결리스트로 구현한 큐
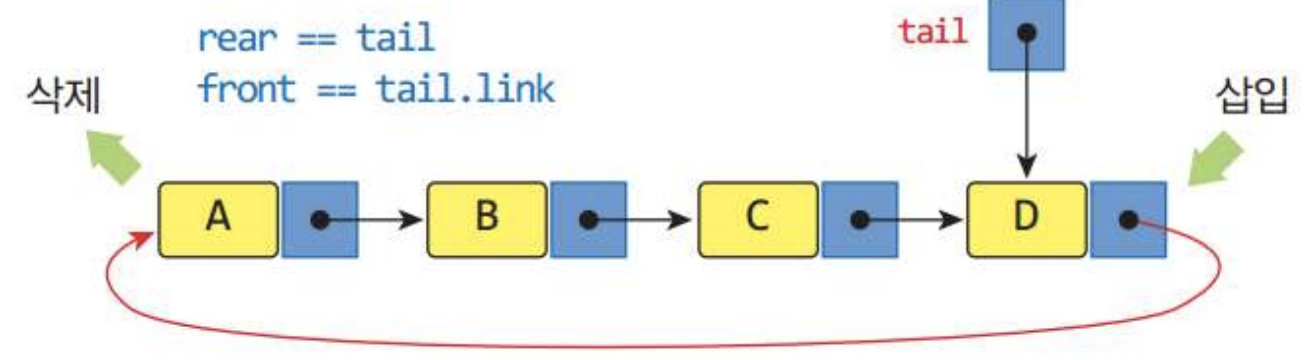
- tail을 사용하는 것이 rear와 front에 바로 접근할 수 있다는 점에서 훨씬 효율적이다
3.1 연결된 큐 클래스
🤜 입력
class CircularLinkedQueue:
def __init__(self):
self.tail = None # tail: 유일한 데이터
def isEmpty(self): return self.tail == None # 공백상태 검사
def clear(self): self.tail = None # 큐 초기화
def peek(self): # peek연산
if not self.isEmpty(): # 공백이 아니면
return self.tail.link.data # front의 data를 반환3.2 삽입 연산: enqueue()
🤜 입력
def enqueue(self,item):
node = Node(item,None) #노드 생성
if self.isEmpty():
node.link = node #새로운 노드가 자신을 가리킴
self.tail = node
else:
node.link = self.tail.link #새로운 노드의 link가 첫번째 노드(self.last.link) 가리킴
self.tail.link = node #tail.link가 첫번째 노드 가리키던거 끊고 새로운 노드 가리킴
self.tail = node #tail도 새로운 노드 가리킴 - 1) Case1: 큐가 공백상태인 경우의 삽입연산
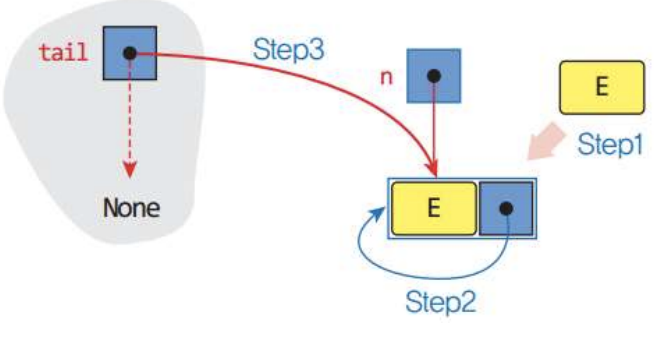
Step1 : node = Node(item,None)
Step2: node.link = node
Step3: self.tail = node
코드와 그림을 참고하면서 코드를 이해해야 한다.
- 2) Case2: 큐가 공백상태가 아닌 경우의 삽입연산
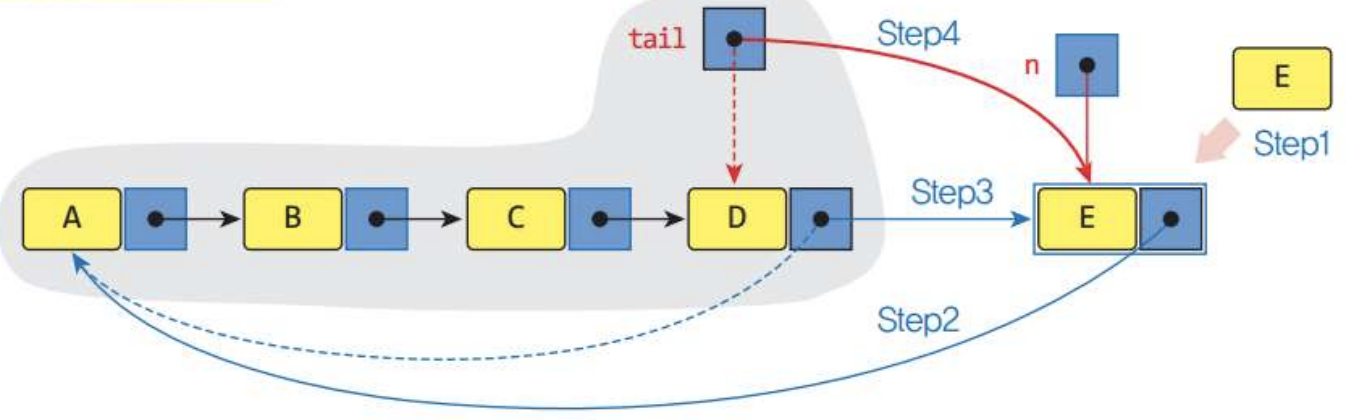
Step1: node.link = self.tail.link
Step3: self.tail.link = node
Step4: self.tail = node
3.3 삭제 연산: dequeue()
🤜 입력
def dequeue(self):
if not self.isEmpty(): #비어있지 않다면
data = self.tail.link.data #데이터=첫번째 노드
if self.tail.link == self.tail: #노드가 하나라면
self.tail = None
else: #노드가 여러개라면
self.tail.link = self.tail.link.link
return data #삭제할 노드 반환 - 1) Case1: 큐가 하나의 항목을 갖는 경우의 삭제연산
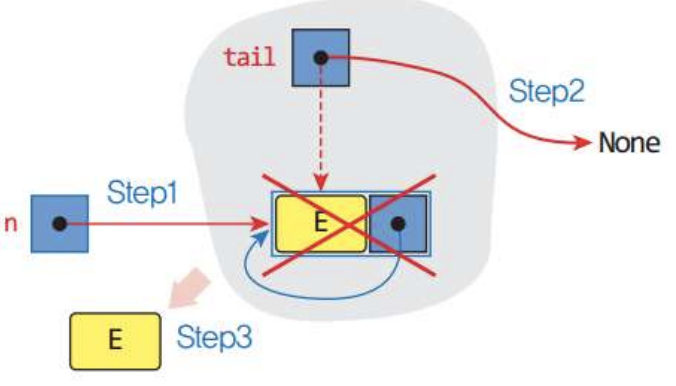
Step1: if self.tail.link == self.tail:
Step2: self.tail = None
- 2) Case2: 큐가 여러 개의 항목을 갖는 경우의 삭제연산
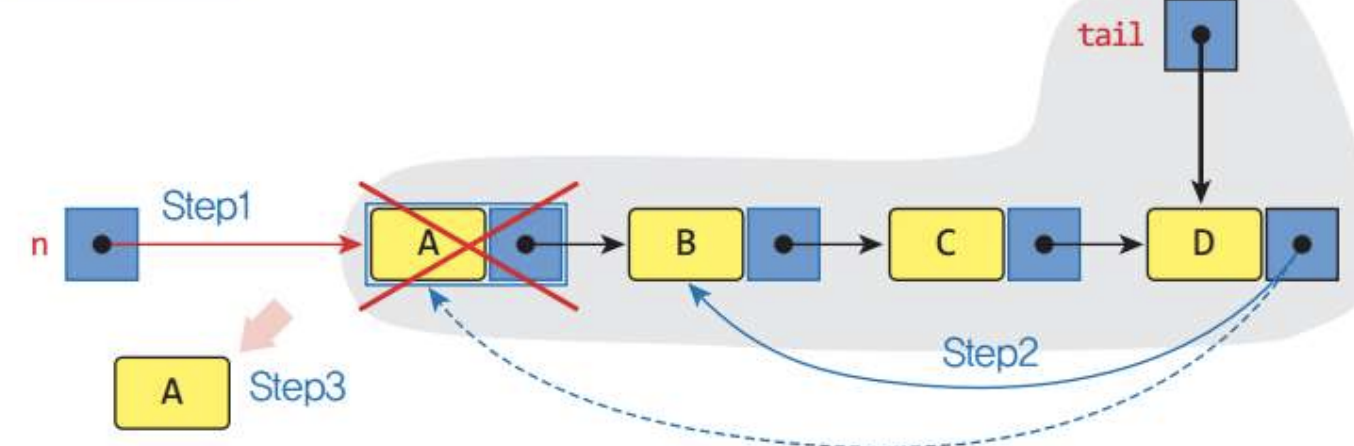
빨간색 X로 된 곳은
self.tail.link이다. 그리고 그 옆 B는self.tail.link.link를 의미한다.
3.4 전체 노드의 방문
🤜 입력
def size(self):
if self.isEmpty(): return 0 # 공백: 0변환
else: # 공백이 아니면
count = 1 # count는 최소 1
node = self.tail.link # node는 front부터 출발 # tail.link=첫번째 노드
while not node == self.tail: #node가 rear가 아닌 동안
node = node.link # 이동
count += 1 # count 증가
return count # 최종 count 반환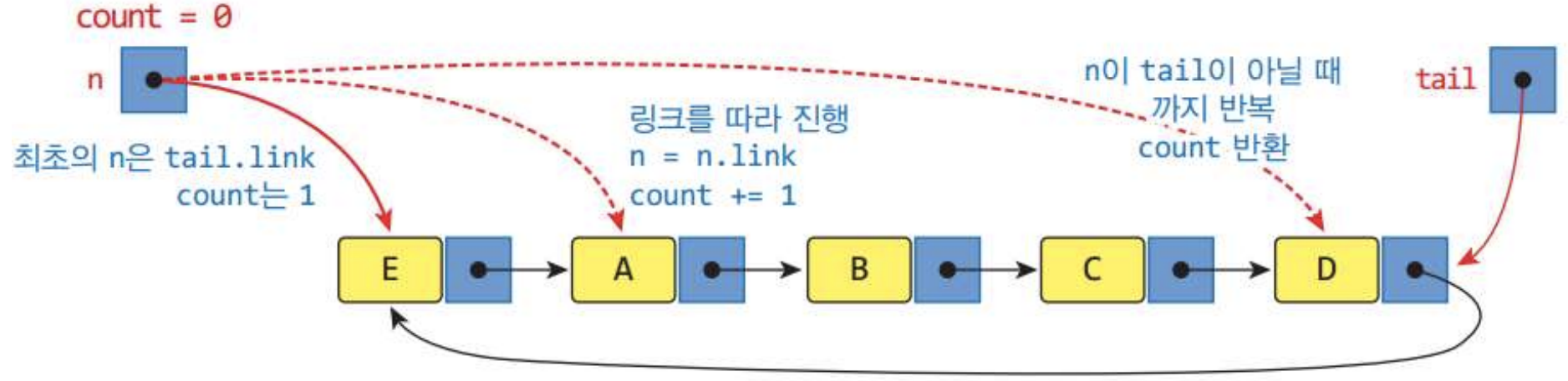
count는 최소 1이다. tail.link는 첫번째 노드를 의미한다.
4. 실행시간
- 리스트로 구현한 큐의 add와 remove연산은 각각 O(1) 시간이 소요된다.
- 하지만 리스트 크기를 확대 or 축소 시키는 경우는 큐의 모든 항목을 복사해야하므로 O(n)시간이 걸린다.
- 단순연결리스트로 구현한 큐의 add와 remove연산은 각각 O(1)시간이 걸린다.
- 삽입 or 삭제 연산이 rear와 front로 인해 연결리스트의 다른 노드들을 방문할 필요없이 각 연산이 수행되기 때문이다.
🎯 Summary
원형 큐는 지금까지 했던 코드 중 제일 이해하기 어려웠다. 단순연결리스트와 원형연결리스트로 구현한 큐를 특히 잘 봐야겠다. 계속 복습해서 내 것으로 만들자!
📚 References
- 양성봉(2022),'파이썬과 함께하는 자료구조의 이해[개정판]', 생능출판, pp.97-101.
- 양태환(2021),'파이썬으로 배우는 자료구조 핵심 원리', 길벗, pp.67-74.
- 큐 그림 출처: https://commons.wikimedia.org/wiki/File:Queue_%28Computer_Science%29.svg
