주제: 파이썬에서 재귀알고리즘 구현하기
파이썬과 함께하는 자료구조의 이해[개정판] pp.30-38 참고해서 내용 작성하였습니다.
파이썬으로 배우는 자료구조 핵심 원리 pp.16-21 참고해서 내용 작성하였습니다.
1. 재귀 알고리즘
정의
: 알고리즘 자신을 사용하여 정의된 알고리즘을 재귀적(recursive)이라고 한다.
- 비재귀적(nonrecursive) 또는 반복적(iterative) 알고리즘과 대조된다.
-
순환은 함수가 스스로를 호출하는 것이다. 이는 팩토리얼, 조합을 계산하기 위한 식의 표현 등에 사용된다.
주의할 점
: 함수가 자기 자신을 호출하도록 프로그래밍 할 때는 무한 호출을 방지해야 한다. -
재귀의 요소
1) 재귀 케이스(recursion)
: 차후의 재귀호출은 작아진 부문제들(subproblems)을 대상으로 이루어진다.
2) 베이스 케이스(base case)
: 부문제들이 충분히 작아지면, 알고리즘은 재귀를 사용하지 않고 이들을 직접 해결한다.
# 예시
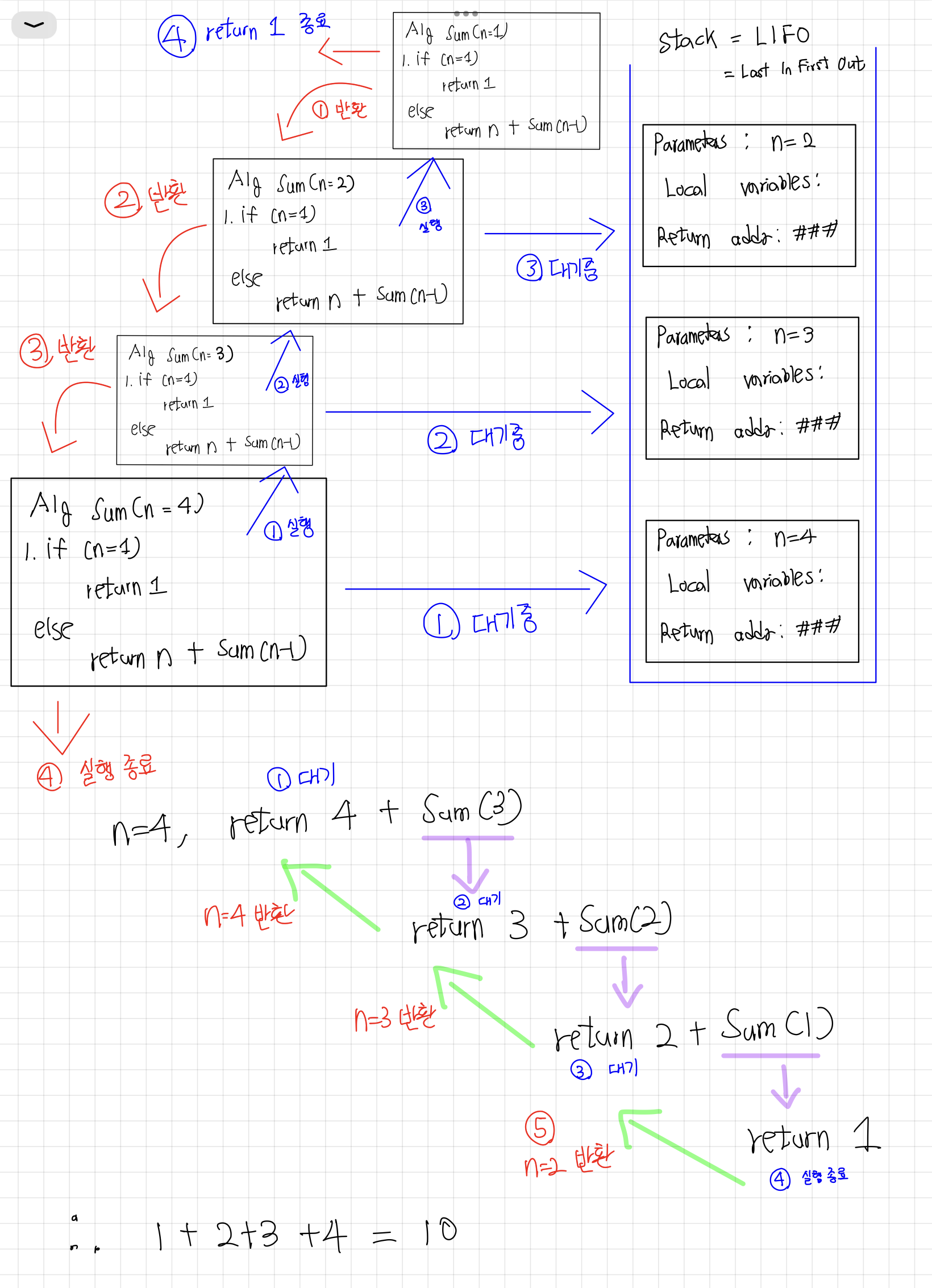
Alg sum(n)
if (n=1): # Base Case
return 1
else:
return n + sum(n-1) # recursion1.1 작동 원리
- 보류된 재귀호출을 위한 변수들에 관련된 저장/복구는 컴퓨터에 의해 자동적으로 수행된다.
- 작동 원리는 밑에 그림과 같다.
1.2 기본 규칙
1) Base Case
- Base Case를 항상 가져야 하며, 이 부분은 재귀 없이 해결 가능하다.
2) 진행 방향
- 재귀적으로 해결되어야 할 경우, 재귀호출은 항상 Base Case를 향하는 방향으로 진행한다.
3) 정상작동 가정
- 모든 재귀호출이 제대로 작동한다는 가정하에 실행한다.
4) 적절한 사용
- 꼭 필요할 때만 사용해야 한다. 왜냐하면 저장 및 복구 때문에 성능 저하가 있을 수도 있기 때문이다.
2. 팩토리얼 구하기
🤜 입력
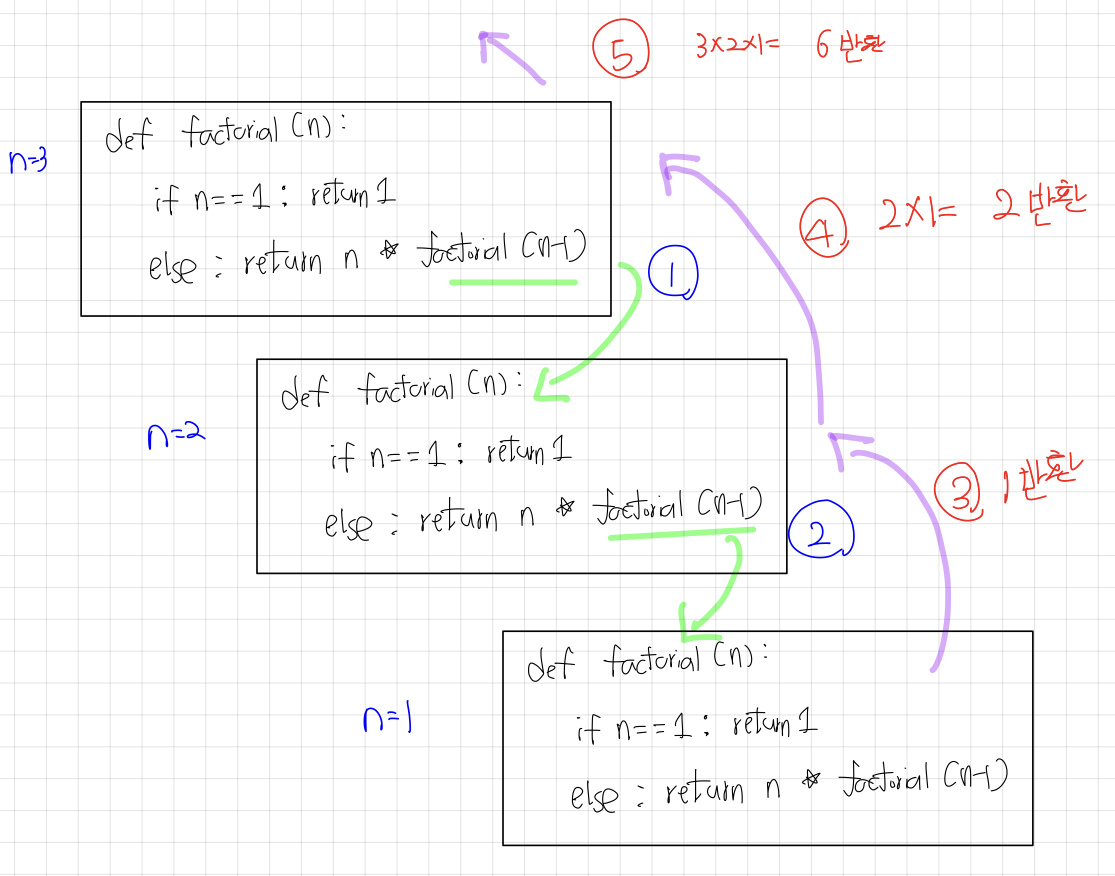
def factorial(n):
if n == 1:
return 1
else:
return n * factorial(n-1)
factorial(3) 💻 출력
6-
순환(recursion): O(n)
: 순환적인 문제에서는 자연스러운 방법이다.
함수 호출의 오버헤드 -
반복(iteration): O(n)
: for or while문을 이용하고, 수행속도가 빠르다
순환적인 문제에서는 프로그래밍이 어려울 수도 있다. 왜냐하면 저장했다가 복귀하는 작업이 없기 때문이다.
대부분의 순환은 반복으로 바꾸어 작성할 수 있다.
2.1 작동 원리
- 보류된 재귀호출을 위한 변수들에 관련된 저장/복구는 컴퓨터에 의해 자동적으로 수행된다.
- 작동 원리는 밑에 그림과 같다.
3. 거듭제곱 계산
3.1. 반복 구조
def power_iter(x,n): # 반복으로 xn을 구하는 함수
return = 1.0
for i in range(n): # 루브: n번 반복
result = result * x
return result- 내부 반복문: O(n)
3.2. 순환 구조
def power(x,n):
if n = 0: return 1
elif (n%2) == 0: # n이 짝수
return power(x*x, n//2) # 정수의 나눗셈
else:
return x * power(x*x, (n-1)//2) # n이 홀수 - 순환적인 함수: O(log2n)
3.3. 시간복잡도
- 순환적인 함수: O(log2n)
- 반복적인 함수: O(n)
거듭제곱 알고리즘은 순환함수를 사용했을 때, 시간복잡도가 logn이므로 n보다 효율적이다.
즉, 거듭제곱 알고리즘은 순환이 더 빠른 예시 중 하나라고 말할 수 있다.
4. 피보나치 수열
정의
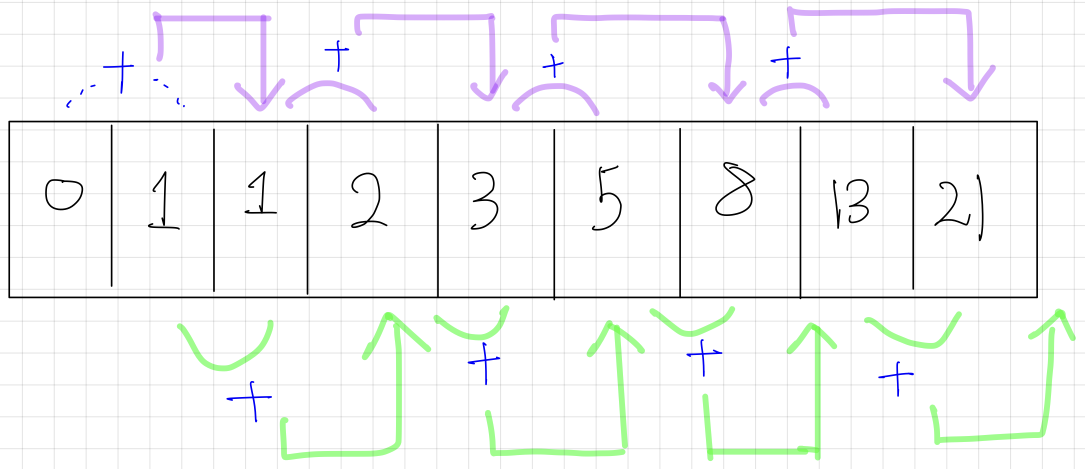
: 피보나치 수는 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다. 처음 여섯 항은 각각 1, 1, 2, 3, 5, 8이다. 편의상 0번째 항을 0으로 두기도 한다.
출처: https://ko.wikipedia.org/wiki/%ED%94%BC%EB%B3%B4%EB%82%98%EC%B9%98_%EC%88%98
- 순환 호출을 사용하면 매우 비효율적인 예시 중 하나이다.
- 피보나치 수열: 0,1,1,2,3,5,8,13,21 ...
4.1 순환구조
🤜 입력
def fib(n): # 순환으로 구현한 피보나치 수열
if n==0: return 0 # 종료조건
elif n==1: return 1 # 종료조건
else:
return fib(n-1) + fib(n-2) # 순환 호출
fib(9)💻 출력
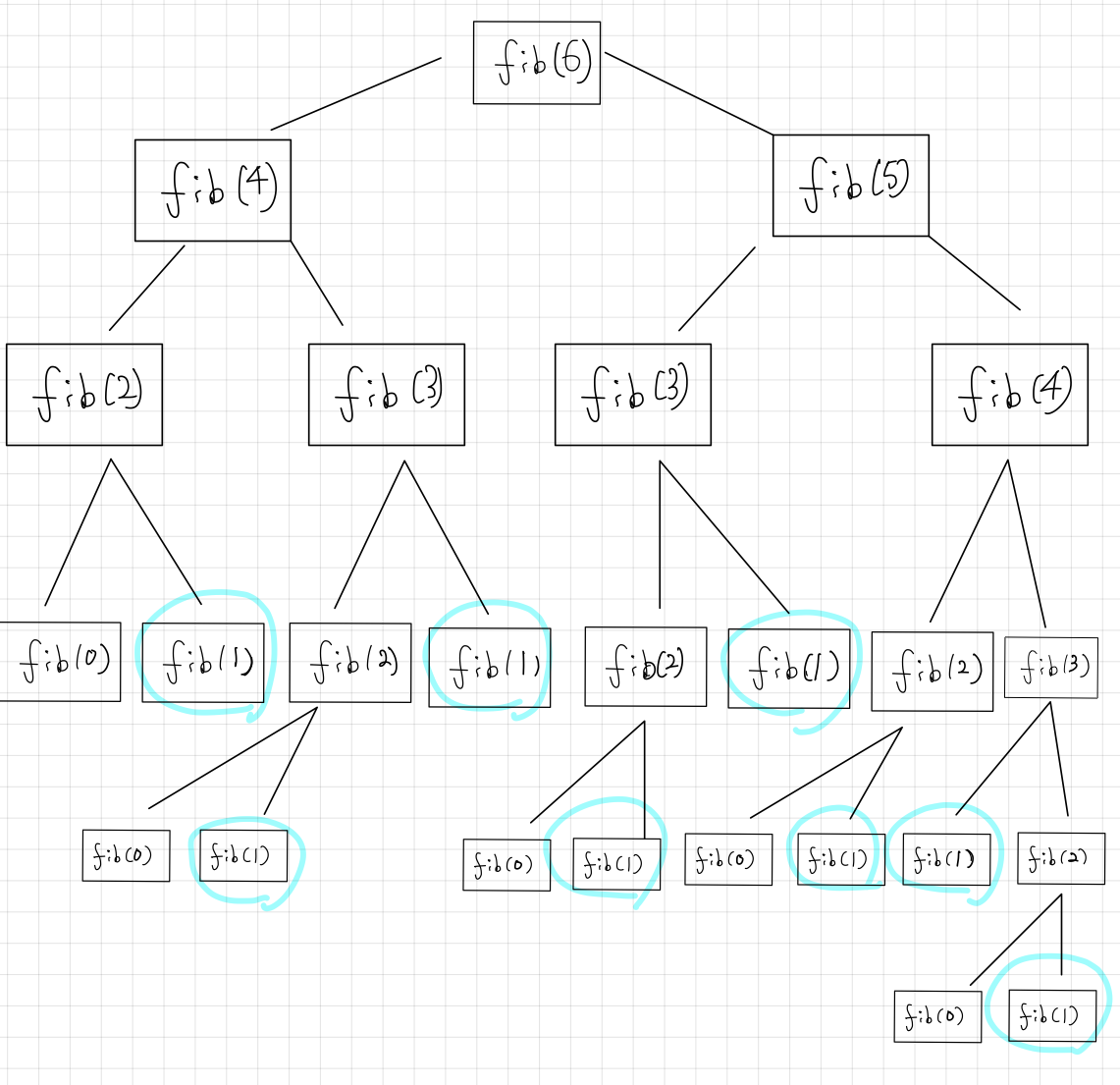
34- 같은 항이 중복해서 계산되기 때문에 밑에 그림과 같이 복잡해지게 되고, 비효율적으로 구성된다.
- 시간 복잡도: O(2^n)
4.2 반복구조
🤜 입력
def fib_iter(n):
if (n<2): return n
last = 0
current = 1
for i in range(2,n+1):
tmp = current
current += last
last = tmp
return current
fib_iter(9) 💻 출력
34- 시간 복잡도: O(n)
4.3 시간복잡도
피보나치 수열 알고리즘은 반복문 을 사용했을 때, 시간복잡도가 n이므로 2^n보다 매우 효율적이다.
즉, 피보나치 수열은 순환이 느린 예시 중 하나라고 말할 수 있다.
5. 우주선 발사 카운트다운
🤜 입력
def countDown(n):
if n==0:
print("발사!")
else:
print(n)
countDown(n-1)
countDown(5)💻 출력
5
4
3
2
1
발사!6. 별 모양 출력
🤜 입력
def printStar(n):
if n>0:
printStar(n-1)
printStar('*'* n)
printStar(5)💻 출력
*
**
***
****
*****별 모양을 거꾸로도 출력할 수 있다.
🤜 입력
def printStar(n):
if n>0:
printStar('*'* n)
printStar(n-1)
printStar(5)💻 출력
*****
****
***
**
*7. 2진수 변환하기
진법이란?
: 수를 표기하는 기수법의 하나로 몇 개의 기본 숫자를 이용하여 수를 표시하는 방법이다.
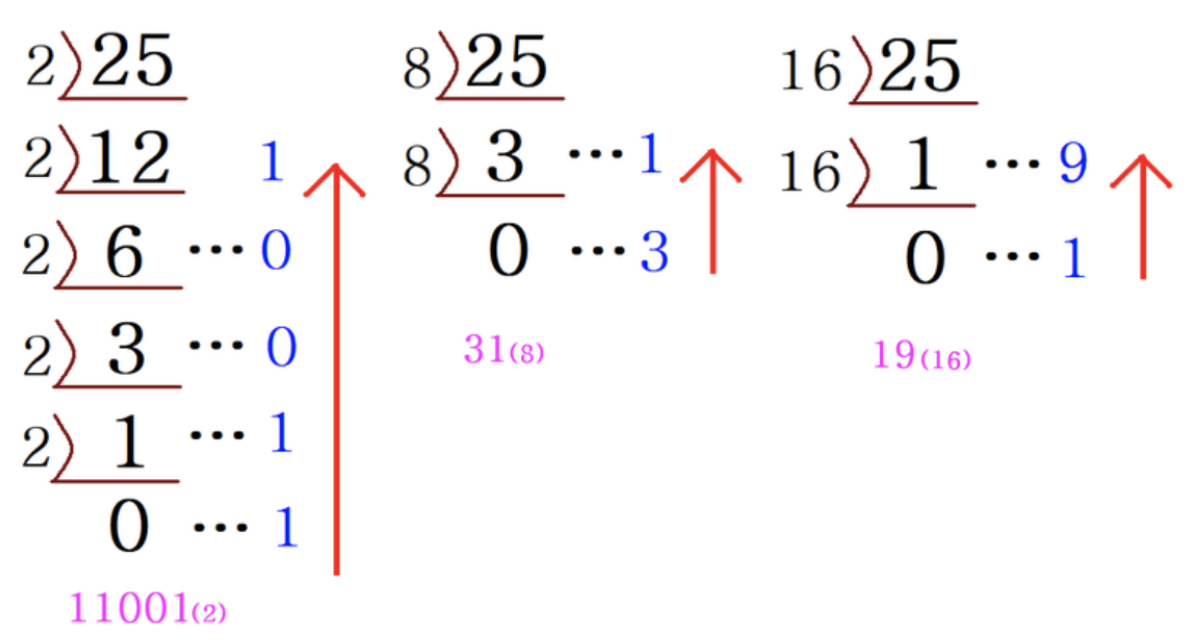
2진수 변환 그림 출처: 티스토리, '[수학] 진법 변환 방법 정리 + 소수점 (2진수, 8진수, 10진수, 16진수)', https://coding-factory.tistory.com/652, 검색일(2023.04.18.).
7.1 비재귀함수 구조
🤜 입력
def notation(base, n): # base: 2,8,10,16진수 / n: 수
if n <0:
rasie ValueError('Number n must n >=0')
digits=''
if n ==0:
digits = numberChar[n]
else:
while n >0:
n,m = divmod(n, base) # divmod는 앞은 나누고 뒤는 나머지를 구해주는 메서드
digits = numberChar[m] + digits
print(digits)
numberChar = ['0', '1','2','3','4', '5', '6', '7', '8', '9']
numberChar += ['A', 'B', "C", "D", "E", "F"]
number = int(input('10진수 입력 -->'))
print('\n 2진수:',end = '') # end = '' 줄 바꿈을 하지 말라는 것
notation(2, number)
print('\n 8진수:',end = '')
notation(8, number)
print('\n 16진수:',end = '')
notation(16, number)💻 출력
10진수 입력 -->13
2진수:1101
8진수:15
16진수:D7.2 재귀함수 구조
🤜 입력
def Binary(base, n):
if n <0:
raise ValueError('Number n must n >=0')
if n < base:
print(numberChar[n], end='')
else:
Binary(base, n//base)
print(numberChar[n%base], end='')
numberChar = ['0', '1','2','3','4', '5', '6', '7', '8', '9','A', 'B', "C", "D", "E", "F"]
number = int(input('10진수 입력 -->'))
print('\n 2진수:',end = '')
Binary(2, number)
print('\n 8진수:',end = '')
Binary(8, number)
print('\n 16진수:',end = '')
Binary(16, number)💻 출력
10진수 입력 -->13
2진수:1101
8진수:15
16진수:D8.하노이 탑 쌓기
정의
: 하노이의 탑(Tower of Hanoi)은 퍼즐의 일종으로 세 개의 기둥과 이 기둥에 꽂을 수 있는 크기가 다양한 원판들이 있고, 퍼즐을 시작하기 전에는 한 기둥에 원판들이 작은 것이 위에 있도록 순서대로 쌓여 있다.
즉, 막대 A(왼쪽)에 쌓여있는 원판 n개를 막대 C(오른쪽)로 옮기는 것이다.
1. 한 번에 한개의 원판만 옮길 수 있다.
2. 가장 위에 있는 원판만 이동할 수 있다.
3. 큰 원판이 작은 원판 위에 있어서는 안 된다.
출처: 위키백과, '하노이의 탑', https://ko.wikipedia.org/wiki/%ED%95%98%EB%85%B8%EC%9D%B4%EC%9D%98_%ED%83%91(검색일: 2023.04.18.).
8.1 재귀함수 구조
🤜 입력
def hanoi_tower(n,fr,tmp, to):
if (n==1): # 종료 조건
print('원판 1:%s --> %s'%(fr,to)) # 가장 작은 원판을 옮김
else:
hanoi_tower(n-1, fr, to, tmp) # n-1개를 to를 이용해 tmp로
print("원판%d: %s --> %s"%(n,fr,to)) # 하나의 원판을 옮김
hanoi_tower(n-1, tmp, fr, to) # n-1개를 fr을 이용해 to로
hanoi_tower(3,"A","B","C") # 3개의 원판이 있는 경우💻 출력
원판 1:A --> C
원판2: A --> B
원판 1:C --> B
원판3: A --> C
원판 1:B --> A
원판2: B --> C
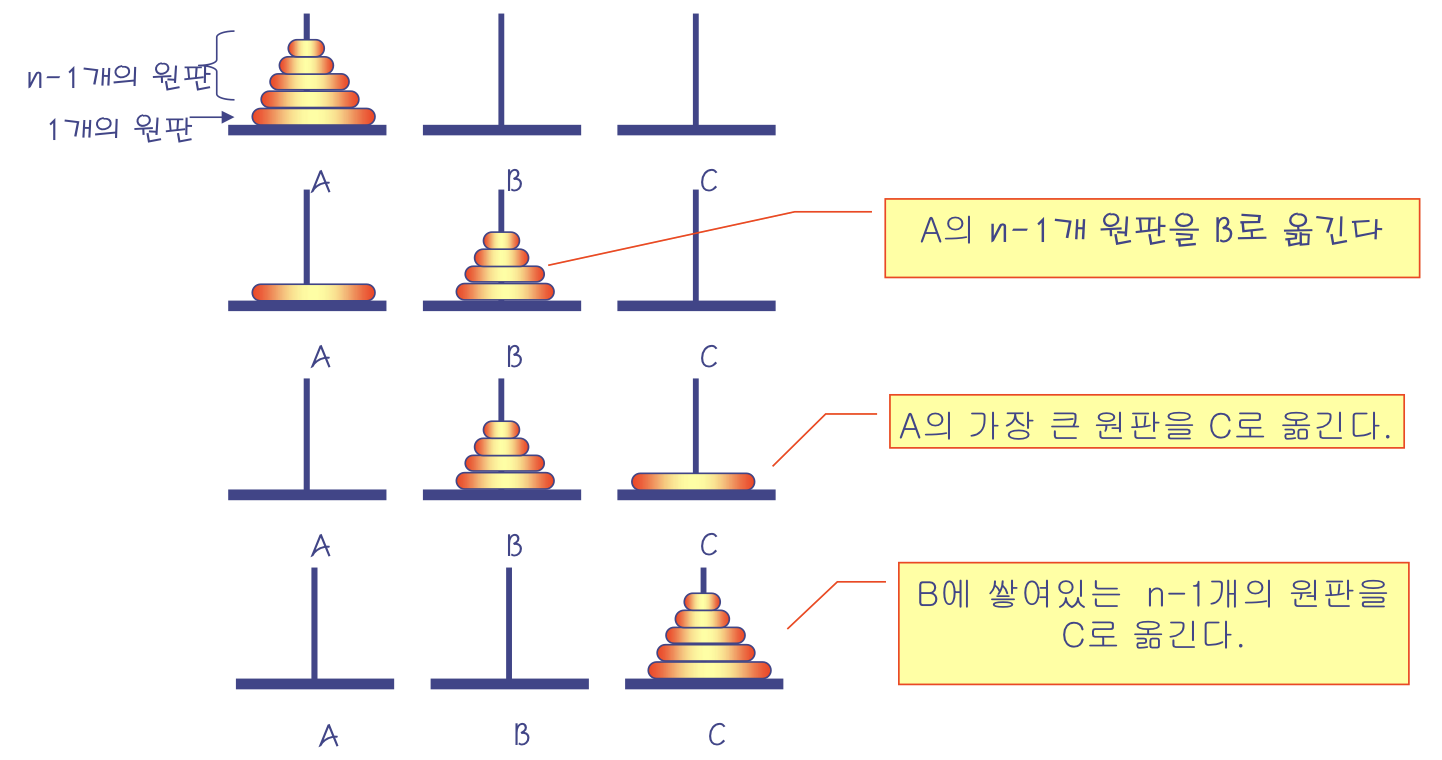
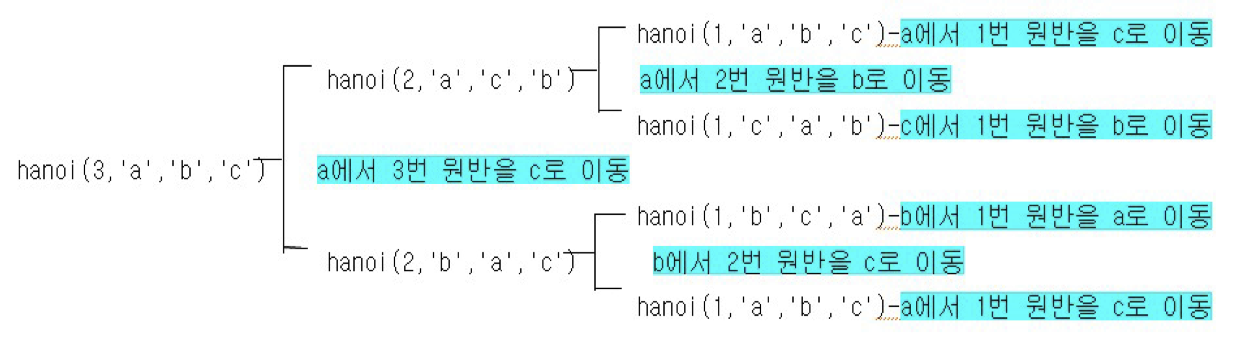
원판 1:A --> C8.2 작동 원리
8.3 비재귀함수 구조
🤜 입력
def move_disk(disk_num, start_peg, end_peg):
print("%d번 원판을 %d번 기둥에서 %d번 기둥으로 이동" % (disk_num, start_peg, end_peg))
def hanoi(num_disks, start_peg, end_peg):
if num_disks == 1: #종료조건
return move_disk(num_disks, start_peg, end_peg)
mid_peg = (6 - start_peg - end_peg)
hanoi(num_disks-1, start_peg, mid_peg)
move_disk(num_disks, start_peg, end_peg)
hanoi(num_disks-1, mid_peg, end_peg)
hanoi(3, 1, 3)💻 출력
1번 원판을 1번 기둥에서 3번 기둥으로 이동
2번 원판을 1번 기둥에서 2번 기둥으로 이동
1번 원판을 3번 기둥에서 2번 기둥으로 이동
3번 원판을 1번 기둥에서 3번 기둥으로 이동
1번 원판을 2번 기둥에서 1번 기둥으로 이동
2번 원판을 2번 기둥에서 3번 기둥으로 이동
1번 원판을 1번 기둥에서 3번 기둥으로 이동9. 나쁜 재귀
1) 잘못 설계된 재귀
- Base Case: 없음
- Recursion: Base Case를 향해 재귀하지 않는다.
2) 나쁜 재귀 사용의 영향은?
- 부정확한 결과를 초래한다.
- 미정지가 된다
- 저장을 위한 기억장소 고갈을 초래한다.
🎯 Summary
무조건 재귀함수를 쓴다고 좋은 것은 아니였다. 특히 피보나치 수열은 재귀함수를 쓸 때, 같은 항이 중복해서 계산되기 때문에 시간 복잡도에서도 O(2^n)이기 때문에 매우 비효율적이다. 알고리즘을 구현할 때, 각 문제마다 코드를 효율적으로 짤 수 있도록 연습해야겠다.
다음은 '연결 리스트' 공부다. 그전까지 철저히 복습을 해야겠다.
📚 References
- 양성봉(2022),'파이썬과 함께하는 자료구조의 이해[개정판]', 생능출판, pp.30-38.
- 양태환(2021),'파이썬으로 배우는 자료구조 핵심 원리', 길벗, pp.16-21.
- 위키백과,'피보나치 수', https://ko.wikipedia.org/wiki/%ED%94%BC%EB%B3%B4%EB%82%98%EC%B9%98_%EC%88%98(검색일: 2023.04.18.).
- 2진수 변환 그림 출처:
티스토리, '[수학] 진법 변환 방법 정리 + 소수점 (2진수, 8진수, 10진수, 16진수)', https://coding-factory.tistory.com/652(검색일: 2023.04.18.). - 위키백과, '하노이의 탑', https://ko.wikipedia.org/wiki/%ED%95%98%EB%85%B8%EC%9D%B4%EC%9D%98_%ED%83%91(검색일: 2023.04.18.).
