1. Ridge 모델 (L2 정규화)
목적:
- 모델의 회귀계수(weight)를 작게 만들어 과적합을 방지하기 위함
특징 :
- 단, feature selection은 되지 않음
- feature의 크기가 결과에 큰 영향을 주기 때문에, Scailing(크기 맞추기)이 매우 중요함
방법:
- 손실 함수에 회귀계수들의 제곱합을 페널티로 추가함
- 이렇게 하면 모델이 복잡해지지 않도록 큰 계수를 억제할 수 있음
즉, 큰 계수를 조금 줄여주고 모든 변수를 살리려고 합니다.
적용 상황:
모든 독립변수가 Y에 약간씩 기여할 때 유용함
사용 과정:
Ridge 모델에서의 손실 함수(Loss function)는 아래와 같습니다.
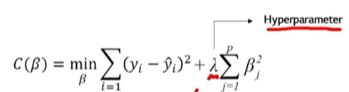
이때, 페널티항의 람다는 하이퍼 파라미터로서 조정할 수 있습니다.
람다에 너무 큰 값을 할당할 경우: 페널티항이 원체 커서, underfitting 됨
람다에 너무 작은 값을 할당할 경우: 페널티항이 너무 작아서, 일반 model처럼 작동함. 즉, overfitting 됨
STEP 1: 회귀계수 초기화
Ridge 회귀는 처음에 각 변수에 대한 회귀계수 b1, b2 등을 초기화합니다.
이때 각 변수는 X1, X2 등으로 불리고, 이 변수들이 예측값 y에 어떤 영향을 미치는지 파악할 것입니다.
STEP 2: 기본 선형 회귀 계산
Ridge 모델이 데이터를 학습하면서,

를 계산합니다.
이는 예측 오차를 최소화하는 방향으로 회귀계수를 조정하는 과정입니다.
STEP 3: 페널티 항 추가
Ridge모델은 여기서 끝나지 않고,
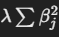
위와 같은 페널티 항을 추가합니다.
이 페널티 항은 계수들의 크기를 제곱한 값을 더해, 큰 계수에 더 큰 페널티를 부과합니다.
즉, 계수가 커질 수록 손실 함수의 값도 커지게 됩니다.
이때, Ridge는 이 손실 함수를 최소화하는 방향으로 계수를 조정하므로, 페널티항 덕분에 특정 변수에 너무 큰 계수가 부여되는 것을 막습니다.
결과적으로, ridge 모델은 큰 계수를 억제하고, 너무 복잡한 모델이 되는 것을 방지합니다!!!
2. Lasso 모델 (L1 정규화)
목적:
- Ridge와 비슷하지만, 특정 변수를 완전히 제외할 수 있음
특징:
- feature selection 가능
- 경사 하강법으로 해를 찾아감
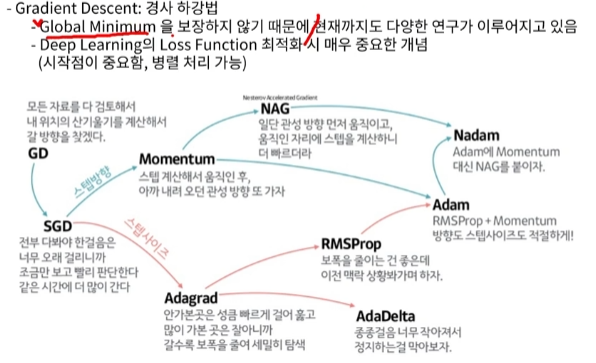
- Local minima에 빠질 수 있으므로, 여러 지점에서 시작하여 해를 동시에 찾아서 최적의 해를 찾을 필요가 있음
- Local minima를 방지하기 위해 momentum을 주어 local minima 지점을 빠져나올 수 있도록 함
방법:
- 손실 함수에 회귀계수들의 절댓값 합을 페널티로 추가함
- 이렇게 하면 일부 계수는 0이 되어 아예 모델에서 제거될 수 있음
즉, 불필요한 변수는 제거하고 중요한 변수만 남기려고 합니다.
적용 상황:
- 중요한 변수가 몇 개만 있을 때 유용 (변수 선택 feature selection에 효과적).
사용 과정:
Lasso 모델에서의 손실 함수(Loss function)는 아래와 같습니다.

STEP 1: 회귀계수 초기화
Lasso 모델도 처음에 각 변수에 대한 회귀계수 b1, b2 등을 초기화합니다.
STEP 2: 기본 선형 회귀 계산
모델이 데이터를 학습하면서, 일반적인 선형 회귀에서와 같이 예측 오차를 줄이는 방향으로 회귀계수들을 조정합니다.
STEP 3: 페널티 항 추가
Lasso모델은 손실 함수에 계수들의 절댓값 합을 페널티로 추가합니다.
이때, Lasso 모델에서는 기여도가 작은 변수일수록 그 변수의 계수를 0으로 수렴하게 됩니다.
기여도가 작은 변수일수록 계수가 0이 되는 이유?
첫 번째: 기여도가 작은 변수는 원래부터 예측에 크게 기여하지 않기 때문에, 그 변수에 할당된 회귀계수(가중치) 가 작습니다.
두 번째: Lasso 모델은 손실 함수에 회귀계수들의 절댓값 합을 더하는데, 이 절댓값을 최소화하려고 하므로 원래 작은 회귀계수에 대해 더 강하게 압박을 가합니다.
즉, 원래 작은 계수일수록 Lasso는 더 쉽게 그 값을 0으로 만들려고 합니다.
세 번째: 불필요한 변수를 제거하고 모델을 간소화하려는 목적에 맞게, 기여도가 작은 변수의 계수를 0으로 만드는 것입니다.
결과적으로, 중요하지 않은 변수는 모델에서 완전히 제외되고, 필요한 변수만 남는 간단한 모델이 됩니다.
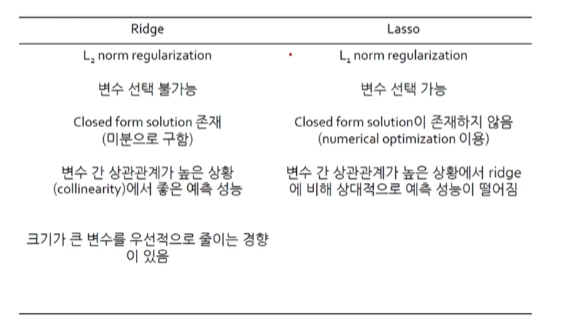
Ridge와 Lasso 장단점 비교
3. ElasticNet (L1+L2 정규화)
특징:
- Ridge와 Lasso의 장점을 결합한 모델
- Ridge와 Lasso보다 더 많은 실험이 필요하다는 단점은 존재함
방법:
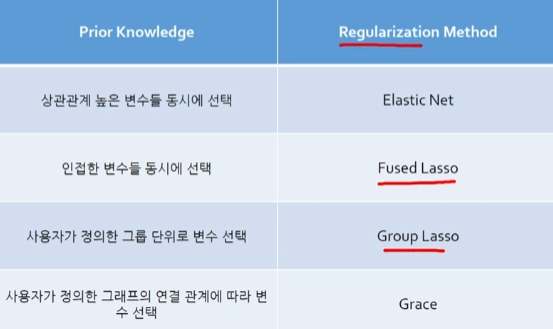
- 손실 함수에 회귀계수의 제곱합(L2) 과 절댓값 합(L1) 을 동시에 페널티로 추가함
- 이로 인해 Lasso처럼 변수를 제거하면서도 Ridge처럼 일부 변수는 유지하게 함
즉, 불필요한 변수를 제거하면서도 너무 많은 변수를 제거하지 않게 조정합니다.
적용 상황:
- 중요한 변수가 몇 개 있을 것 같지만, 모든 변수가 Y에 어느 정도 영향을 줄 수 있을 때 유용.
그 외
🔵 흥미로웠던 점:
파이썬 코드를 쓰면서도 모델이 어떻게 중요한 feature를 뽑아내는지 궁금했는데, 그 원리를 알게 되어 가려운 곳을 긁어주는 듯 했다.
🔵 다음 학습 계획:
SQL 데이터 분석 실습을 하며 Tableau 툴에 대해 배울 예정입니다.