완전탐색알고리즘

완전 탐색 알고리즘이란, 이름과 같이 정말로 완~~~전 무식하게 모든 요소를 다 탐색해서 문제를 해결하겠다는 뜻이다.

원래는 브루트 포스는 암호학에서 사용되었던 용어라고 한다. 모든 경우의 수를 다 탐색해서 기어코 해킹을 하겠다는 인간의 도전의식이 담긴 알고리즘이라고 할 수 있다.

그도 그럴것이, 예를들어 4자리의 랜덤 숫자로 이루어진 자물쇠가 있을 때, 시간제한없이 이 암호를 푼다면 저 금고안의 금괴를 다 주겠다고 누군가 말했다면 누구라도 완전탐색을 해서라도 비밀번호를 찾고자 할 것이다.

완전탐색알고리즘은 공간복잡도와 시간복잡도의 요소를 전혀 고려하지 않는다. 최악의 시나리오를 취하더라도 문제를 해결하려는 방법이다.

그렇다면 이 무식한 해결방법인 Brute Force Algorithm은 언제 사용할까?

1. 프로세스 속도를 높이는데 사용할 수 있는 다른 알고리즘이 없을 때
2. 해결해야할 문제의 솔루션을 모두 각각 확인해야할 때

for문을 통해 어떤 값을 찾기위해 하나씩 비교하는 코드를 보면 이도 마찬가지로 범위를 줄이지 않고 하나하나 비교하기 때문에 브루트 포스 알고리즘을 사용한 문제해결이라고 볼 수 있다.

문제가 복잡하지 않고 시간과 컴퓨팅자원이 풍부하다면 브루트포스 알고리즘(완전탐색 알고리즘)을 사용해도 무방하다. 그러나 데이터규모가 크고 문제의 복잡도가 높아진다면 정확도를 조금 희생하더라도 더 효율적인 알고리즘을 사용하는 것이 좋다.

Brute-Force Algorithm 알고리즘의 사용예시

1. 순차 검색 알고리즘

• 배열로 정리된 데이터에서 값을 검색할 때 0번 인덱스부터 마지막 인덱스까지 순차적으로 모두 검색한다.

  for(int i = 0; i < n; i++) {
     if(arr[i] == K) {
       result = true;
     }
   }
   return result;

  ---

2. 문열 매칭 알고리즘

• 문자열 두 개를 입력받아 패턴을 포함하는지 검색한다.

public boolean BruteForceStringMatch(String[] arr, String[] patternArr) {
/*
     Brute Force 문자열 매칭 구현하기
     --------------------------------------------------------
     입력1. n개의 문자 텍스트를 나타내는 배열 arr,
     입력2. m개의 문자 패턴을 나타내는 배열 patternArr
     --------------------------------------------------------
     출력: 일치하는 문자열이 있으면 첫번째 인덱스를 반환한다. 검색에 실패한 경우 -1을 반환.
*/
    
    int n = arr.length;
    int m = patternArr.length;
    for (int i = 0; i <= n - m; i++) {
       /*
       전체 요소개수에서 패턴개수를 뺀 만큼만 반복.
       그 수가 마지막 비교요소이기 때문이다.
       i 반복 문은 패턴과 비교의 위치를 잡는 반복문입니다.
       */
      
      int j = 0; // j는 전체와 패턴의 요소 하나하나를 비교하는 반복문.
      
      while (j < m && patternArr[j].equals(arr[i + j])) {
        // j가 패턴의 개수보다 커지면 안되기때문에 개수만큼만 반복.
        // 패턴에서는 j인덱스와 전체에서는 i + j 인덱스의 값이 같은지 판단.
        // 같을때 j에 +1.
       
       j = j + 1;
      }
      if (j == m) {
        // j와 패턴 수가 같다는 것은 패턴의 문자열과 완전히 같은 부분이 존재한다는 의미.
        // 이 때의 비교했던 위치를 반환.
        return true;
      }
   }
   return false;
 }

---

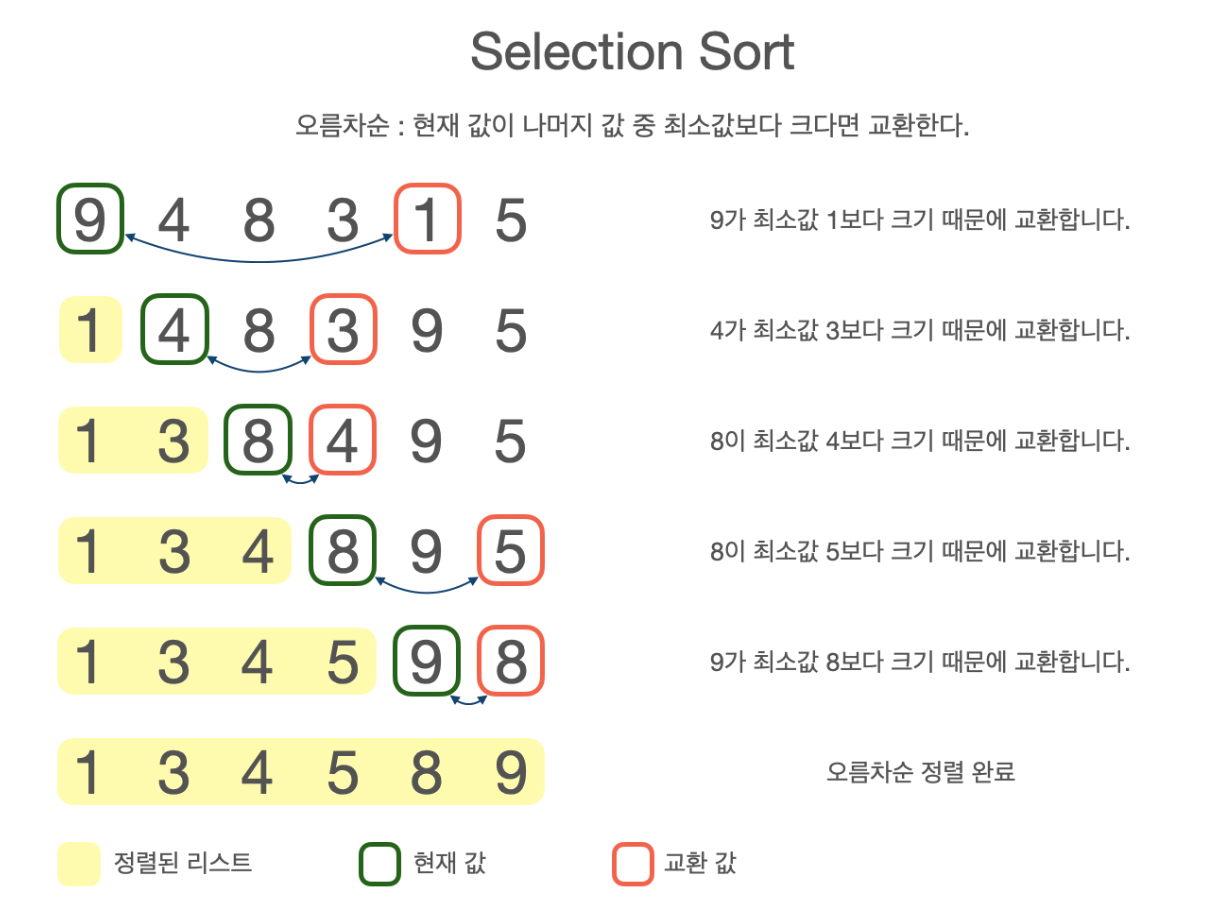
3. 선택정렬 알고리즘

• 전체배열을 검색해서 현재요소와 나머지 값을 비교함. 현재요소보다 더 작거나 크다면 데이터를 교환하는 정렬 알고리즘.
  

public int[] SelectionSort(int[] arr) {
    // 주어진 배열을 Selection Sort로 오름차순 정렬.
    // 입력: 정렬 가능한 요소의 배열 A
    // 출력: 오름차순으로 정렬된 배열
    
    for (int i = 0; i < arr.length - 1; i++) {
      int min = i;
      for (int j = i + 1; j < arr.length; j++) {
        // 현재 i에 +1을 j로 반복문을 초기화하고 i 이후의 배열요소과 비교하는 반복문을 구성.
        if (arr[j] < arr[min]) {
          // j인덱스의 배열 값이 현재 인덱스의 배열 값보다 작다면
          min = j;
          // j 인덱스를 최소를 나타내는 인덱스로 할당.
        }
      }
      
      // 반복문이 끝났을 때(모든 비교가 끝났을때)
      // min에는 최소값의 인덱스가 들어있음.
      // i값과 최소값을 바꿔서 할당함.
      int temp = arr[i];
      arr[i] = arr[min];
      arr[min] = temp;
    }
  // 모든 반복문이 끝나면 정렬된 배열을 반환함.
  return arr;
}