Max Heap in python

Choog Yul Lee·2023년 3월 9일

🔍 About Max Heap

최대 힙(Max Heap)은 트리의 마지막 단계(Level)에서 오른쪽을 뺀 나머지 부분이 가득 채워져 있다는 점에서 완전 이진 트리이다. 그리고 각 노드의 원소가 자식들의 원소보다 크다는 특성을 갖는다. 따라서 루트는 트리의 가장 큰 원소가 된다.

Max Heap 특성

완전 이진 트리이다.

각 노드의 원소가 자식들의 원소보다 크다

루트는 노드의 가장 큰 원소가 된다.

Heap은 최소 힙(Min Heap)과 최대 힙(Max Heap)으로 구분할 수 있는데,
Max Heap은 각 노드의 원소가 자식들의 원소보다 크다는 특성을 갖고,
Min Heap은 각 노드의 원소가 자식들의 원소보다 작다는 특성을 갖는다.

🏷️ Requirement

내가 구현하려는 Max Heap의 요구사항은 두 가지이다.

Max Heap 의 특성을 을 유지하면서 노드를 삽입하는 insert 함수를 구현하라.
Max Heap 의 특성을 을 유지하면서 최대 노드를 삭제하는 extract_max 함수를 구현하라.

⛏️ Implement

일반적으로 Max Heap 은 배열(Array) 자료구조를 활용하여 구현하게 되는데, 배열을 활용하는 이유는 인덱스를 사용하여 접근할 수 있기 때문이다. 아래의 그림은 부모 노드 Index와 자식노드 Index사이에 특별한 규칙 표현하고 있다. Heap 이 어떻게 배열로 대칭되는지 쉽게 확인 할 수 있다.

※ 구현의 편의를 위해 배열의 시작 인덱스는 1부터 시작하는 것으로 한다.

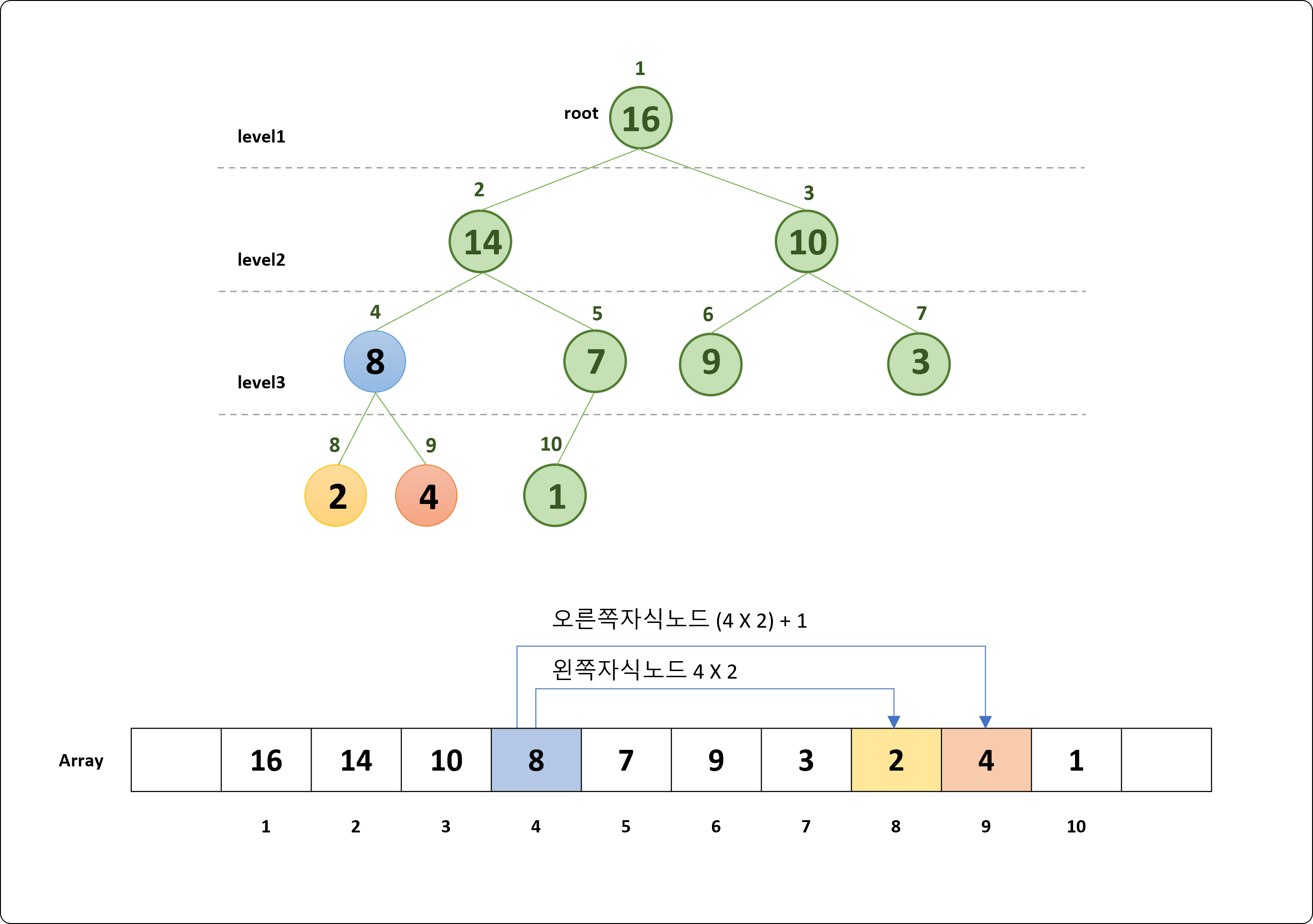
규칙

왼쪽 자식 노드 인덱스 = 부모 노드 인덱스 X 2

오른쪽 자식 노드 인덱스 = ( 부모 노드 인덱스 X 2 ) + 1

부모 노드 인덱스 = 자식 노드 인덱스 / 2

규칙을 python code으로 표현하면 아래와 같다. 이 함수들을 구현에 활용한다.

def __get_parent_node_index(self, parent_index):
	return parent_index // 2

def __get_left_child_node_index(self, parent_index):
	return 2 * parent_index

def __get_right_child_node_index(self, parent_index):
	return (2*parent_index) + 1

def __is_leaf(self, parent_index):
	max_index = self.__get_max_index()

	return (parent_index * 2) > max_index

def __get_max_index(self):
	return len(self.maxheap) - 1

📍 MaxHeap Class를 정의한다.

구현의 편의를 위해 배열의 시작 인덱스는 1부터 시작하는 것으로 했으므로
MaxHeap Class의 __init__는 0번 index에는 None을 입력하고, 1번 index에는 인자로 받은 value를 값을 저장하도록 한다.

class MaxHeap:
    def __init__(self, value):
        self.maxheap = list()
        self.maxheap.append(None)
        self.maxheap.append(value)

📍 MaxHeap Class에 `insert` 기능을 구현한다.

MaxHeap에서 insert 함수의 구현은 2 Step으로 나누어 생각한다.

데이터를 마지막에 삽입한다.
부모노드와 비교하여 값이 크다면, 부모노드와 위치를 바꾼다.

def insert(self, value):
	# 1. just insert the value at the end
	self.maxheap.append(value)
	# 2. if the child node value is greater than the parent node, replace iteratively

	current_index = len(self.maxheap) - 1

	while (True):
		is_swap, parent_node_index = self.__is_moveup(current_index)

		if(not is_swap):
		   break;
		
		self.maxheap[parent_node_index], self.maxheap[current_index] = 
        self.maxheap[current_index], self.maxheap[parent_node_index]
		current_index = parent_node_index
		
		
def __is_moveup(self, current_index):
	return_value = False

	parent_node_index = self.__get_parent_node_index(current_index)

	if (parent_node_index == 0):
		return return_value, parent_node_index

	if(self.maxheap[parent_node_index] < self.maxheap[current_index]):
		return_value = True
		return return_value, parent_node_index

	return return_value, parent_node_index

📍 MaxHeap Class에 `extract_max` 기능을 구현한다.

MaxHeap에서 extract_max 함수의 구현은 3 Step으로 나누어 생각한다.

최상단 노드(Root) 를 삭제한다.
가장 마지막에 추가한 노드를 Root 노드에 복사한다.
Root 노드 값이 Child 노드 보다 작을 경우, Root 노드의 Child 노드 중 가장 큰 값을 가진 노드와 Root 노드 위치를 바꾸주는 작업을 반복한다.

def __is_movedown(self, current_index):
	return_value = False

	if(self.__is_leaf(current_index)):
		return return_value, current_index
	else: 
		left_child_node_index = self.__get_left_child_node_index(current_index)
		right_child_node_index = self.__get_right_child_node_index(current_index)
		max_index = self.__get_max_index()

		# has just left node
		if (right_child_node_index > max_index):
			if(self.maxheap[left_child_node_index] > self.maxheap[current_index]):                    
				return_value = True
				return return_value, left_child_node_index
			else:
				return_value = False
				return return_value, current_index
		# has two children node
		else:
			greater_value_node_index = self.__get_greater_value_node_index(left_child_node_index, right_child_node_index)
			if(self.maxheap[greater_value_node_index] > self.maxheap[current_index]):                    
				return_value = True
				return return_value, greater_value_node_index
			else:
				return_value = False
				return return_value, current_index   

def extract_max(self):
	current_index = 1
	max_value = self.maxheap[1]
	last_node_value = self.maxheap.pop()

	self.maxheap[1] = last_node_value

	while(True):
		is_movedown, child_node_index = self.__is_movedown(current_index)
		if(not is_movedown):
			break;
				
		self.maxheap[child_node_index], self.maxheap[current_index] = 
        self.maxheap[current_index], self.maxheap[child_node_index]
		current_index = child_node_index

	return max_value

📍 Max Heap Class에 기능을 확인한다.

이제 구현된 Max Heap Class 의 기능을 점검한다.

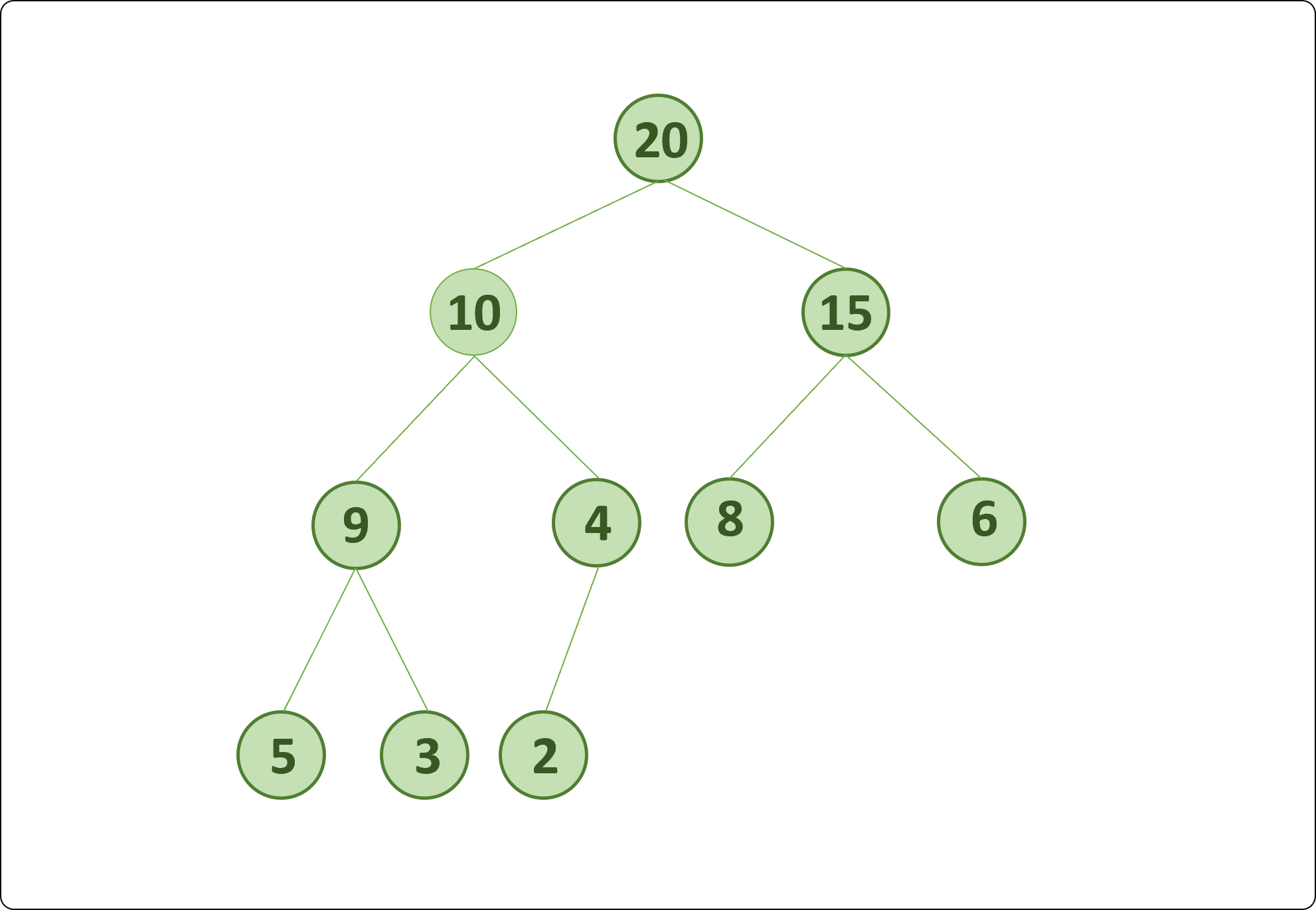
insert 기능 확인 : 위 모양의 Max Heap를 insert 함수를 통해 만들고 값을 출력한다.

extract_max 기능 확인 : extract_max 를 이용해 값을 삭제 했을 때 Heap 의 특성이 유지되는지 확인한다.

insert 기능 확인

maxheap = MaxHeap(15)
maxheap.insert(10)
maxheap.insert(8)
maxheap.insert(5)
maxheap.insert(4)
maxheap.insert(20)
maxheap.insert(6)
maxheap.insert(9)
maxheap.insert(3)
maxheap.insert(2)

maxheap.print()

output

parent_value : 20 left_child_value : 10 right_child_value : 15
parent_value : 10 left_child_value : 9 right_child_value : 4
parent_value : 15 left_child_value : 8 right_child_value : 6
parent_value : 9 left_child_value : 5 right_child_value : 3
parent_value : 4 left_child_value : 2

extract 기능 확인

extract_value = maxheap.extract_max()
print("Extract Value : " + str(extract_value))
maxheap.print()

output

Extract Value : 20
parent_value : 15 left_child_value : 10 right_child_value : 8
parent_value : 10 left_child_value : 9 right_child_value : 4
parent_value : 8 left_child_value : 2 right_child_value : 6
parent_value : 9 left_child_value : 5 right_child_value : 3