
🔍 About Binary Search Tree
이진 탐색 트리(Binary Search Tree)는 최대 두 개의 자식 노드를 가지는 트리형태의 자료구조로, 아래의 특징을 갖는다.
- 이진트리는 루트가 있다.
- 모든 노드가 적어도 두 개의 자식 노드를 가진 정렬 트리이다.
- 루트 트리는 당연히 레벨(루트로부터의 거리)이라는 개념을 가지고 있다.
- 모든 노드에 대해서 하위 레벨로 연결되는 노드로 자식 노드의 개념을 정리할 수 있다.
위 이진 트리의 특성에 아래 네가지 특성을 더 하면 이진 탐색 트리가 된다.
- 각 노드에 값이 있다.
- 값들은 전순서가 있다.
- 노드의 왼전 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져 있다.
- 노드의 오른쪽 서브트리에는 그 노드의 값보다 큰 값들을 지닌 노드들로 이루어져 있다.
- 좌우 하위 트리는 각각이 다시 이진 탐색트리여야 한다.
🏷️ Requirement
내가 구현하려고 하는 이진탐색트리의 요구사항은 총 4가지이다.
- 노드를 검색하여 값이 존재하면 노드를 리턴한다.
- 노드를 검색하여 값이 존재하지 않으면
None을 리턴한다. - 이진 탐색 트리를 유지하면서 노드를 삽입한다.
- 이진 탐색 트리를 유지하면서 노드를 삭제한다.
⛏️ Implement
📍 데이터를 저장하는 Node Class를 정의한다.
Node 클래스는 노드값(value)와 좌/우 노드(left, right) 이렇게 총 세 개의 속성을 갖는다.
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def __str__(self):
return str(self.value) 📍 Binary Search Tree를 유지하며 Node를 관리할 BinarySearchTree Class 를 정의한다.
class BinarySearchTree:
pass📍 BinarySearchTree Class 에 insert 기능을 구현한다.
새로운 값은 트리의 잎 노드에 연결된다. 구현 할 때 고려해야 할 사항은 새로운 값을 연결시킬 잎 노드의 부모 노드를 찾는 것이다.
root가None이면root에insert_node를 연결시킨다.insert_node보다 크면 오른쪽으로,insert_node보다 작으면 왼쪽으로 순회하면서leaf node를 찾는다.- 크면 오른쪽에, 작으면 왼쪽에
insert_node를 연결시킨다.
def insert(self, value):
insert_node = Node(value)
# if first
if self.root is None:
self.root = insert_node
return
current_node = self.root
# search parent node for linking
while current_node is not None:
if current_node.value < value:
parent_node = current_node
current_node = current_node.right
else:
parent_node = current_node
current_node = current_node.left
# connect parent node with insert node
if(parent_node.value < value ):
parent_node.right = insert_node
else:
parent_node.left = insert_node📍 BinarySearchTree Class 에 Inorder Traversal 기능을 구현한다.
Inorder Traversal은 중위 순회라고 한다. 중위 순회는 다음과 방법으로 진행된다.
- 왼쪽 서브트리를 중위 순회한다.
- 노드를 방문한다.
- 오른쪽 서브 트리를 중위 순회 한다.
간략히 이야기 하면 Left -> Root -> Right 순서로 노드를 방문한다. 트리를 중위 순회하면 노드의 값을 오름차순으로 방문하게 된다. 그래서 중위 순회는 이진 탐색 트리에서 값을 찾을 때 많이 사용된다.
def inorder(self):
stack = []
current_node = self.root
while((current_node is not None) or (len(stack) != 0)):
if(current_node is not None):
# print("current node:" + str(current_node.value))
# print("current left:" + str(current_node.left.value))
stack.append(current_node)
current_node = current_node.left
else:
parent_node = stack.pop()
print(parent_node.value)
current_node = parent_node.right📍 BinarySearchTree Class 에 search 기능을 구현한다.
BinarySearchTree 에서 값을 찾아 해당 노드를 Return하는 함수를 구현한다.
- subtree root 값과 찾으려 하는 값을 비교한다.
- 값이 동일하면 종료한다.
- 값이 크면 오른쪽 서브트리로 이동한다.
- 값이 작으면 왼쪽 서브트리로 이동한다.
- 값을 찾을때 까지 1번과 4번을 반복한다.
- 값이 존재하지 않으면
None을 리턴한다.
def search(self, search_value):
current_node = self.root
while current_node is not None:
if(current_node.value == search_value):
return current_node
if(current_node.value > search_value):
current_node = current_node.left
else:
current_node = current_node.right
return None📍 BinarySearchTree Class 에 delete 기능을 구현한다.
원하는 노드를 삭제하는 함수를 구현한다. 삭제기능의 구현은 조금 까다로운데, 삭제 후에도BinarySearchTree의 특성을 유지해야 하기 때문이다. 자식 노드가 없다면 그냥 삭제하면 되지만 자식노드가 존재하는 경우는 어떻게해야 하나? 노드를 삭제하고 나면 자식 노드들과의 연결이 다 끊겨서 접근이 불가능해 질 텐데 말이다.
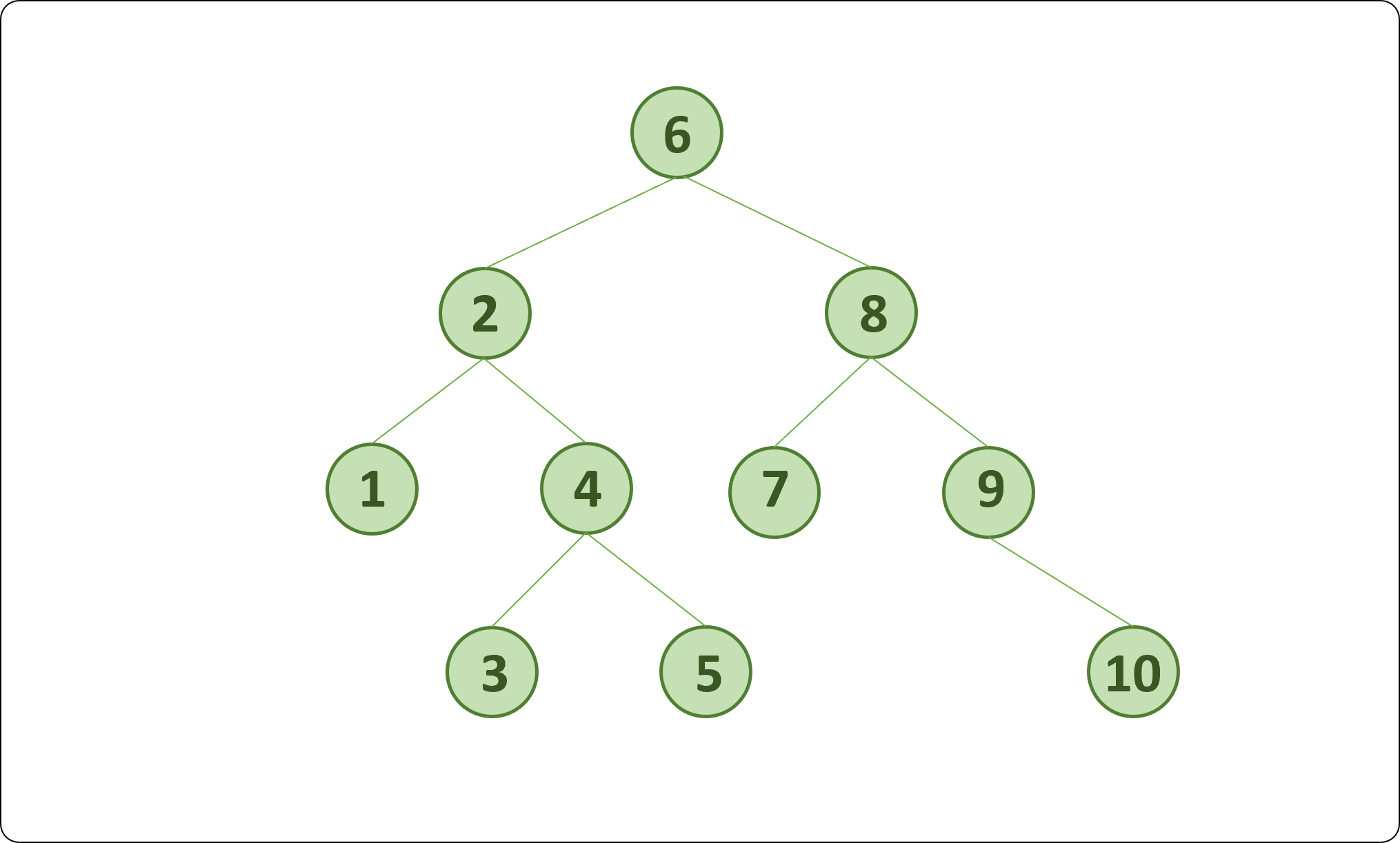
아래의 그림에서 값 4를 가진 Node를 삭제하면, 저 저리에 어떤 노드를 두어야 BinarySearchTree의 특성 유지할 수 있을지 고민해야 한다.

전체를 한 번에 바라 보려면 어렵게 때문에 BinarySearchTree에서 삭제는 3가지 경우의 수로 나누어 생각한다.
Case1. Leaf Node, 자식이 없는 노드를 삭제할 때
- 단순히 삭제 한다.
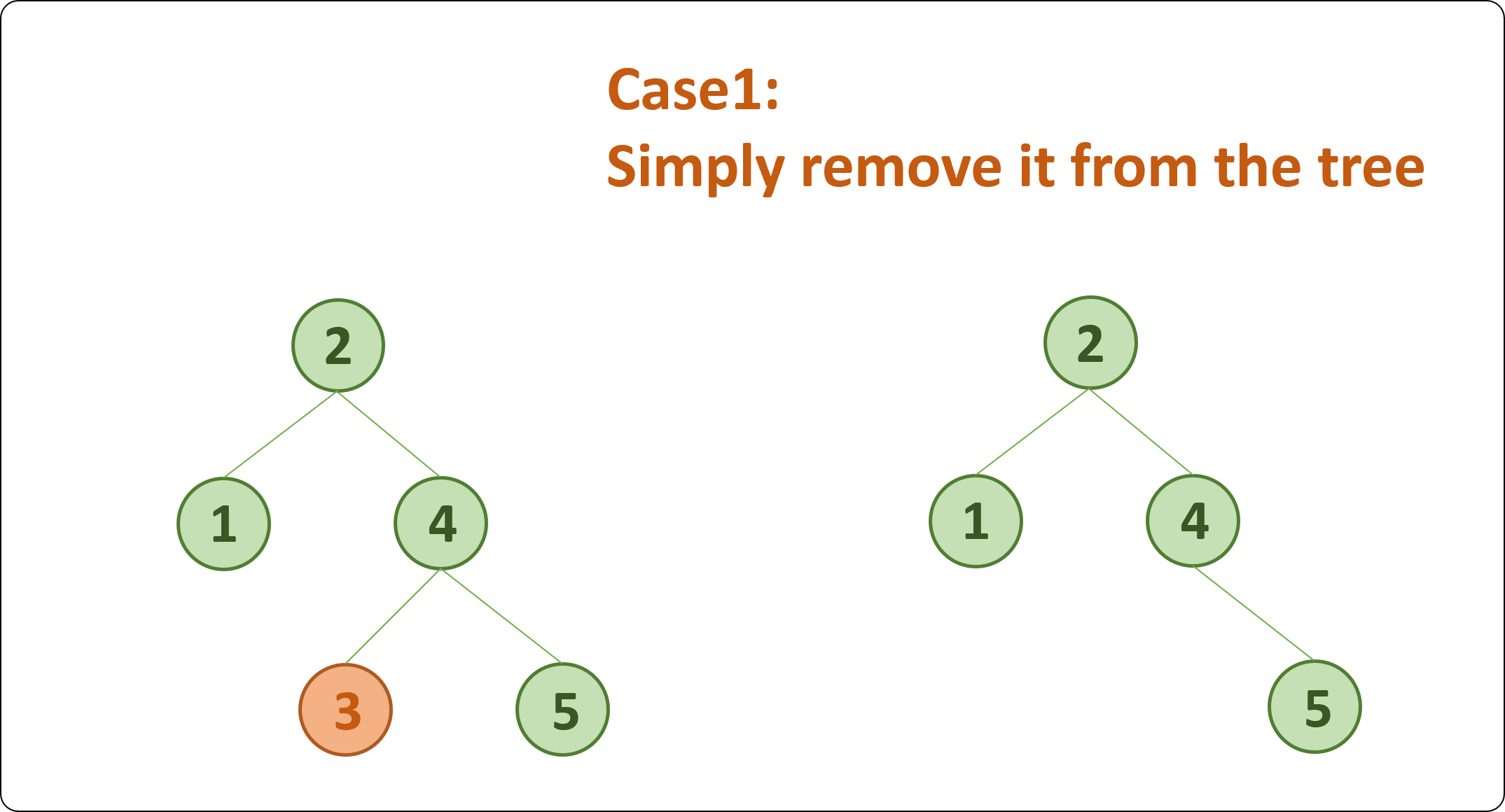
Case2. 자식을 하나 가지고 있는 노드를 삭제할 때
- 자식 노드를 삭제할 노드에 복사한다.
- 노드를 삭제한다.
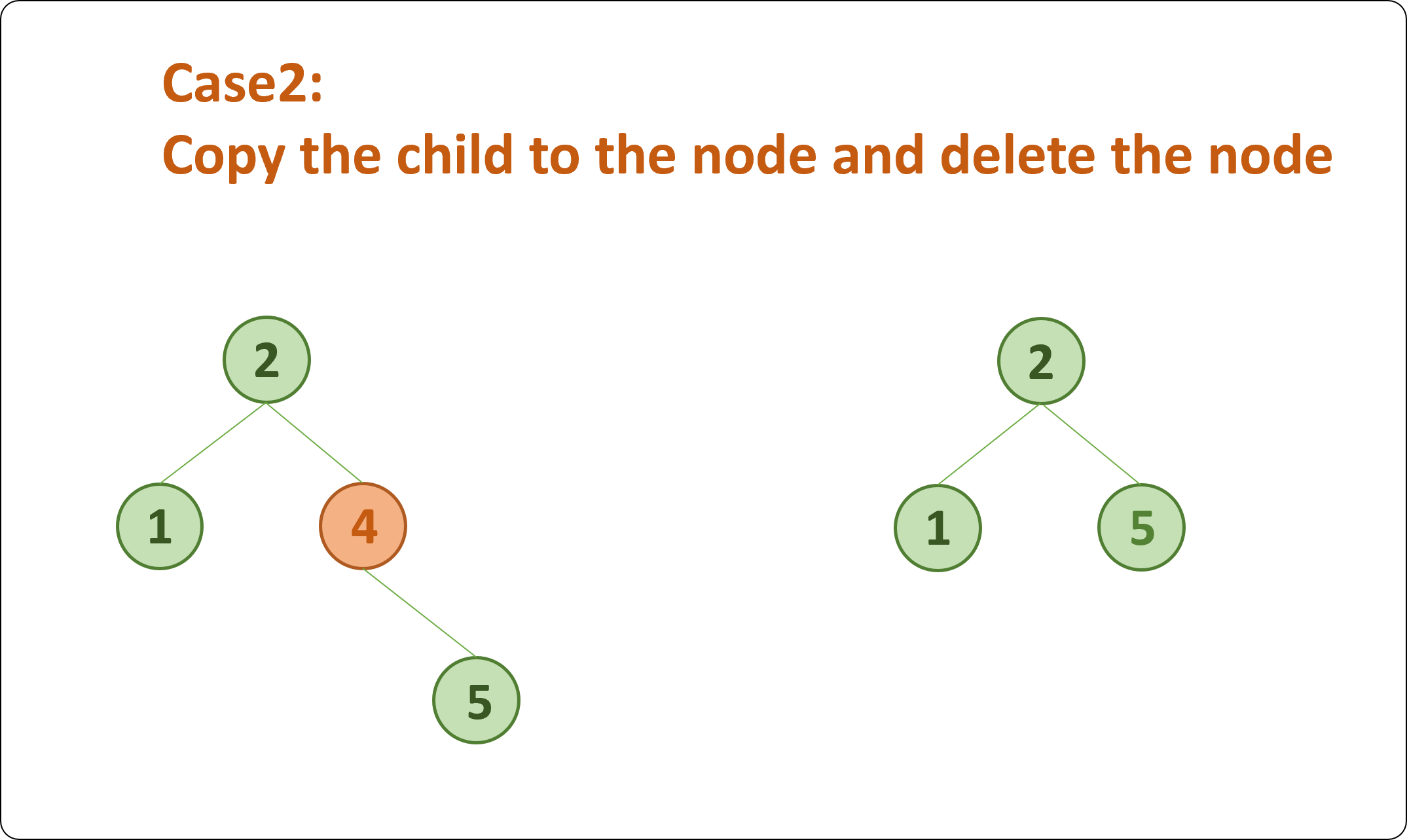
Case3. 자식을 두개 가지고 있는 노드를 삭제할 때
- 후임자(삭제할 노드의 오른쪽 자식 중 가장 작은 값)를 가진 노드를 찾는다.
- 후임자를 삭제할 노드에 복사한다.
- 노드를 삭제한다.
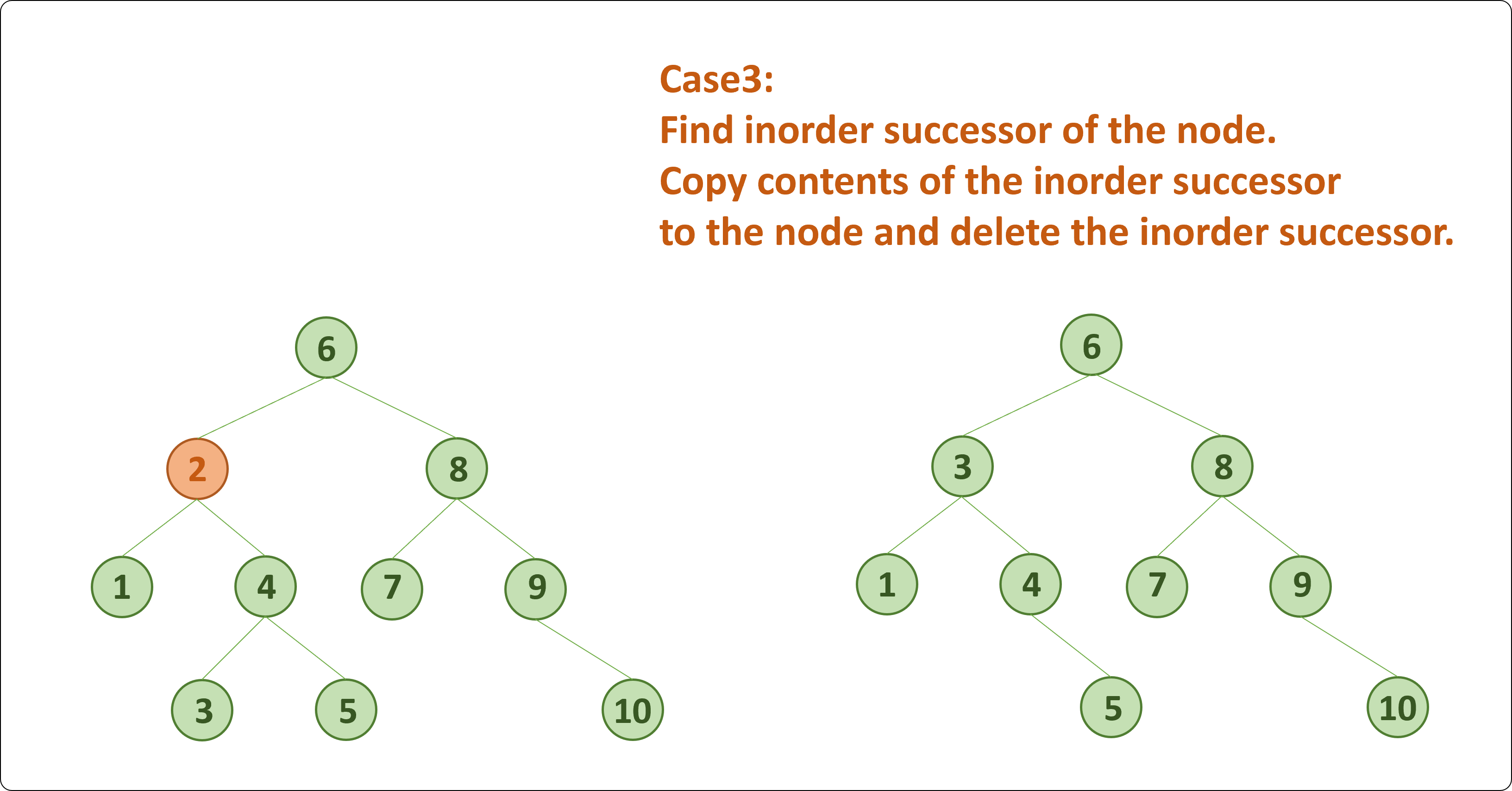
이를 Loop와 Reclusive(재귀함수)를 사용하여 각각 구현하면 아래와 같다.
Loop를 이용한 구현
def delete_using_loop(self, delete_value):
# step1. search node
current_node = self.root
parent_node = self.root
search = False
while current_node is not None:
if current_node.value == delete_value:
search = True
break
parent_node = current_node
if current_node.value > delete_value:
current_node = parent_node.left
else:
current_node = parent_node.right
if current_node is None:
print("can not find the node you want to delete")
return search
# step2. delete
# case 1. leaf node
if current_node.left is None and current_node.right is None:
del(current_node)
if parent_node.value > delete_value:
# print("greater than :" + str(parent_node.value))
parent_node.left = None
else:
# print("less than: " + str(parent_node.value))
parent_node.right = None
# End case 1.
return
# case 2. only one child
if current_node.left is None or current_node.right is None:
if parent_node.value > delete_value:
if current_node.left is not None:
parent_node.left = current_node.left
else:
parent_node.left = current_node.right
else:
if current_node.left is not None:
parent_node.right = current_node.left
else:
parent_node.right = current_node.right
# End case 2.
return
# case 3. two children
if current_node.left is not None and current_node.right is not None:
minimum_parent_node = current_node.right
minimum_node = minimum_parent_node
while minimum_node.left is not None:
temp = minimum_node
minimum_node = minimum_parent_node.left
minimum_parent_node = temp
# print('minimum node value : ' + str(minimum_node.value))
if parent_node.value > delete_value:
parent_node.left = minimum_node
else:
parent_node.right = minimum_node
if minimum_node.left is None and minimum_node.right is None:
minimum_parent_node.left = None
minimum_node.left = current_node.left
minimum_node.right = current_node.right
elif minimum_node.left is None and minimum_node.right is not None:
minimum_node.left = current_node.left
del(current_node)
# End case 3.
return재귀를 이용한 구현
def search_min_node(self, root):
if root.left is None:
return root
else:
minimum = self.search_min_node(root.left)
return minimum
def delete_using_reclusive(self, delete_value):
self._delete_value(self.root, delete_value)
def _delete_value(self, root, delete_value):
if root is None:
return
if root.value > delete_value:
root.left = self._delete_value(root.left, delete_value)
elif root.value < delete_value:
root.rigth = self._delete_value(root.right, delete_value)
else:
# case 1. leaf node or only one child
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
else:
# case 2. it has two children.
# search minimum node
minimum = self.search_min_node(root.right)
# copy minimum node
root.value = minimum.value
# delete minimum node
root.right = self._delete_value(root.right, minimum.value)
return root📍 BinarySearchTree의 기능을 확인한다.
아래 모양의 BinarySearchTree를 insert 함수를 통해 만들고, search 함수를 통해 값을 검색해 보고, 두 개의 delete 함수를 사용하여 노드를 삭제해 보면서 기능을 검증한다.

insert기능 확인
bst = BinarySearchTree()
bst.insert(6)
bst.insert(2)
bst.insert(1)
bst.insert(4)
bst.insert(3)
bst.insert(5)
bst.insert(8)
bst.insert(7)
bst.insert(10)
bst.insert(9)
bst.inorder()output
1
2
3
4
5
6
7
8
9
10search기능 확인
searched_node = bst.search(7)
if searched_node is not None:
print("search value: " + str(searched_node.value))
else:
print("There is no data.")output
search value: 7delete기능 확인
# case3: delete the node has 2 children
bst.delete_using_loop(2)
# case2: delete the node has only child
bst.delete_using_reclusive(9)
# case1: delete leaf node
bst.delete_using_loop(1)
bst.inorder()output
3
4
5
6
7
8
10