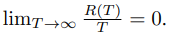논문 소개

https://arxiv.org/abs/1412.6980
모델링 과정에서 매개변수가 어떻게 학습이 되는지 머릿속으로 그려볼 필요가 있었다. Optimizer의 종류에 따라 손실함수 f의 움직임이 달라진다. 다양한 Optimizer의 중심이라고 할 수 있는 Adam을 자세히 읽어보았다.

INTRODUCTION

목적함수에 확률성, 랜덤성이 있음을 가정한 상태에서 AdaGrad, RMSProp으로부터 영감을 받아 Adam을 설계했음을 설명하고 있다. 다른 optimizer처럼 first gradient step을 사용함으로써 메모리 전략을 강조하면서도 first and second moments of the gradients를 통해 adaptive learning을 유도하고 있다.

SGD, AdaGrad, RMSProp을 아래와 같이 간단하게 정리했다.

ALGORITHM

Adam의 알고리즘은 이와 같다.

알고리즘만 보는건 어질어질하니 ,,, 수식으로 재표현하면서 이해해보자 !

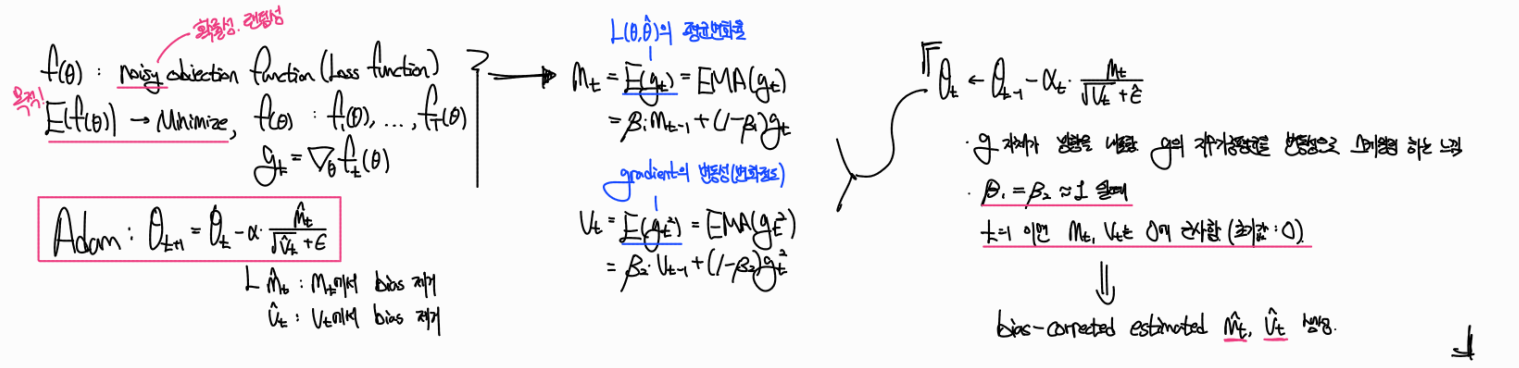
여기서 중요한 점은 여타 알고리즘처럼 $g$를 그대로 사용하지 않고 $E(g)$를 사용했다는 점과, $E(g)=mt$와 $E(g^2)=vt$를 지수가중평균으로 구성했다는 점, 그리고 bias-corrected estimated를 활용하여 편향을 제거한 점이다. bias-corrected estimated는 논문 뒷쪽에 자세히 설명되어있다.

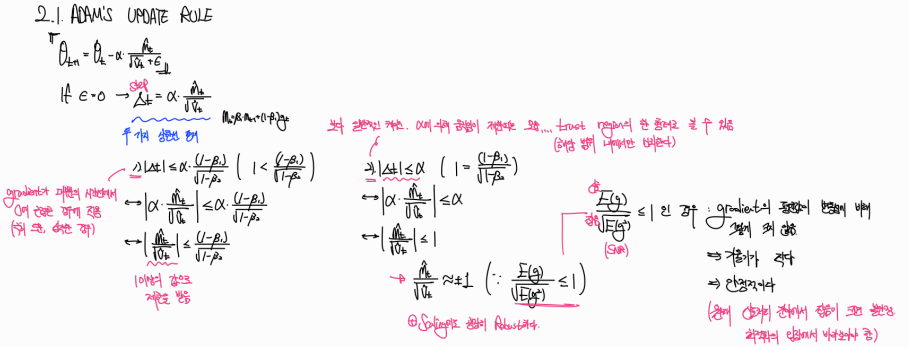
Adam의 update rule에서 엡실론을 0으로 잡았을 때, step을 구성하는 SNR은 두 가지의 상한선이 존재한다고 한다. 이를 1)과 2)로 구분해서 설명하는데, 1)은 step의 상한이 높아지는 불안정한 상황을 의미하게 된다. 일반적인 경우는 2)인데, 이는 $(1-b_1)=(1-b_2)^{1/2}$인 상황이고 $SNR$이 1보다 작거나 같은 안정적인 경우라고 볼 수 있다. 안정적이라고 볼 수 있는 이유는 최적화에서는 $signal$$($신호, 기울기$)$가 클수록 불안정하기 때문이다.
(** 원래 신호처리에서 $SNR$은 값이 클수록, 즉 잡음이 신호에 비해 약할수록 안정적이다. 최적화의 관점에서 바라보아야 하며 저자도 이에 대해 $SNR$이라는 용어가 abused되었음을 명시하고 있다.)

INITIALIZATION BIAS CORRECTION

Adam은 initialization bias correction term을 사용한다. 해당 논문에서는 vt(second moments of the gradients)를 기준으로 설명했지만, mt(first moments of the gradients)도 마찬가지의 원리를 가진다. 나는 읽으면서 직관적인 해석과 통계학적인 해석으로 나누어서 살펴보았다.

1. 직관적 해석
   gradiant의 평균 $mt$와 변동성 $vt$는 $t=0$일 때 $0$으로 초기화하게 된다. 이때 $t=1$이 되면 $m1, v1$이 실제 값보다 작아진다. 이는 $(1-b1)$으로 인해 발생하는 문제이며, 해당 수식으로 나눠줌으로써 문제를 해결할 수 있다.
   (** 사실 변동성이라는 용어를 사용하면 안된다. 정확히는 uncentered variance, 즉 중심화되지 않은 분산이라고 표현된다. 이는 "중심으로부터 분포의 퍼짐 정도"를 보는 것이 아니라 "확률변수 X에서의 변동 정도의 평균"을 의미하는 것이다. 하지만 의미적으로 유사하기에 편의상 '변동성' 용어를 정리하고자 한다.)
   

2. 통계적 해석
   해당 논문에서 $vt$를 기준으로 설명하기에, 정리도 $vt$로 했다. $t$를 $0$부터 하나씩 넣어보면 $vt$를 summation term으로 정리할 수 있고, 분포가 존재한다는 가정 하에 vt에 Expectation을 씌움으로써 $E(g^2)$와의 관계를 확인했다. 아래 정리처럼 $(1-b2^2)$로 나눠주어 $vt$를 불편추정량으로 유도할 수 있다.
   

CONVERGENCE ANALYSE

Adam의 convergence를 분석하는 파트이다. 데이터 포인트 마다의 변화를 관측하기 위해 online learning framework 방식을 가져갔으며, Regret을 정의하고 그 상한을 증명함으로써 Adam의 convergence를 정당화했다.

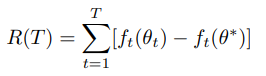
Theorem 4.1를 살펴보면 $R(T)$의 상한을 정의하는 summation term이 설명되어있다.

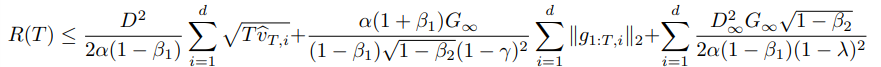
data feature가 sparse하고 bounded gradient를 가질수록 기존의 상한보다 Regret이 작아질 수 있음을 설명하고 있다.
(개인적인 생각 -> data의 feature가 sparse하다면 $R(T)$가 낮아지고, 이는 시간에 따른 후회지수의 상한이 낮아질 수 있음을 시사하며 최적값을 향하는 step의 누적 이동거리가 낮아지는 것을 의미하게 된다. 때문에 data feature가 sparse한 경우 learning rate를 낮추는 것이 학습에 유리하지 않을까라는 생각을 했다.)

앞의 가정들이 충족할 때, $T>=1$에 대해서

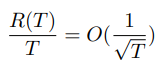
가 충족한다. $R(T)/T$는 평균을 의미하고, 이 상태에서 $T$가 무한대로 간다면 평균적으로 후회는 없어짐을 수식적으로 증명하고 있다.