논문 소개

https://www.researchgate.net/publication/352321708_TS-Bert_Time_Series_Anomaly_Detection_via_Pre-training_Model_Bert

해당 논문은 2021년에 나온 논문으로 트랜스포머 계열 모델을 시계열 문제에 적용하려고 시도한 연구이다. 시계열에 LLM을 접목하여 유의미한 성능을 얻었다는 부분에서 분명 의의가 있다고 생각한다. 전체 내용을 다루기 보다는 중요한 부분만 가져와서 리뷰하도록 하겠다.

INTRODUCTION

대규모의 monitoring data를 분석하는 것은 기업에게 매우 중요하며, 때문에 monitoring system에서로부터 생성된 large volume of time series에서 potential error와 anomaly를 분석하는 것은 굉장히 중요하다. 하지만 저자는 기존에 널리 채택된 CNN, RNN, LSTM과 같은 모델들은 long-distance dependency에서 자유로울 수 없기에, self-attention으로 이를 해결한 transformer계열의 Bert모델을 시계열 문제에 적용하고자 했다. TS-Bert는 기존의 Bert와 같이 pre-training(MLM, NSP)과 fine-tuning과정을 거치게 된다. TS-Bert의 강점은 unsupervised model인 것이며, 이것이 가능한 이유는 SR를 활용한 labeling이 가능하기 때문이다.

-> 사실 unsupervised model라고 표현하는 게 맞나 싶다. 엄밀히 따지면 SR로 라벨링하고, 학습 과정에서 TS-Bert가 라벨링된 결과를 학습하기 때문에 supervised model이다. 아마 라벨링 과정 또한 같은 프로세스에 넣음으로써 label이 없는 데이터에서 anomaly detection이 가능하다고 표현한 것 같다.

실험은 KPI dataset과 yahoo dataset으로 진행하였으며, 기존의 SOTA solution에 비해 각각 21%, 11% 높은 정확도를 기록했다고 한다.

METHODOLOGY

Time series anomaly detection(TSAD)에서 문제 정의는 다음과 같이 이루어질 수 있다.

즉, timestamp 만큼의 차원 공간 R^n에 T가 존재하며, 이때 task는 해당 공간에 있는 output vector Y를 생성하는 작업으로 생각할 수 있다.

해당 연구에서는 위 TSAD 문제를 TS-Bert로 다루게 된다. 모델의 robustness를 증가시키기 위해 모든 time series dataset은 정규화된 상태이다. 또한 기존의 Bert는 TSAD task를 해결하기 위해 설계되지 않았으므로 detection accuracy를 높이기 위한 수정 작업을 거치게 된다. 아래 그림은 TS-Bert의 구조이다. 기존의 Bert처럼 Pre-training 과정에서 NSP와 Mask LM 학습을 수행함으로써 양뱡향적 시계열성 정보를 학습하게 되며, Fine-tuning과정에서 SR를 활용한 labeling 작업 후 anomaly detection을 수행하게 된다.

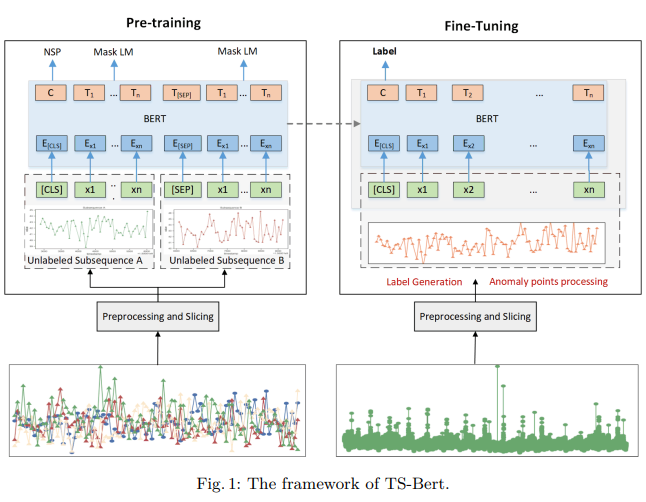
Data Preprocessing

Data preprocessing은 Min-max scaling을 사용한다. 여기서 scale을 곱하게 된다.

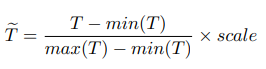
scale을 곱하는 이유는 Min-max scaling값 자체는 0~1사이의 실수값이기에, 정수값을 input으로 기대하는 Bert에 맞출 필요가 있기 때문이다.

Pre-training

Pre-training과정에서는 기존의 Bert와 마찬가지로 Masked LM과 Next Sentence Prediction을 수행하게 된다. 이 때, input data로 사용되는 time series data에는 anomaly가 없다고 가정한다.
알고리즘 형태는 다음과 같다(아마 4번 줄에서 xi에 tilde가 붙지 않은 것은 오타인 듯 하다...)

논문에 Step별로 자세히 소개가 되어있으므로 간략히 느낌만 적자면, scaling된 x를 window size(Li)만큼 자르되 길이가 pw인 subsequence가 여러 개 생성되는 것이고, 각각의 subsequence인 sj가 di에 들어감으로써 subsequence vector의 집합 di가 생성된다. 그 상태에서 Bert에 데이터를 학습시켜 Pre-trained된 Bert model을 얻게 된다.

Fine-tuning

Fine-tuning과정에서도 마찬가지로 scaling을 거친다. 이후, SOTA anomaly detection method인 SR(Spectral Redisual)을 활용해 라벨을 생성한다. 라벨은 0, 1 값을 가진다. 알고리즘 형태는 다음과 같다.

이 때, 이상치 지점을 slicing window의 평균지점으로 환산하여 정상 시계열로 변환해주는 작업을 거쳐서 학습한다. 이를 통해 보다 Robust하게 이상치를 탐지할 수 있게 된다. 모델이 이상치에 대해 오버피팅하는 것을 방지하고, 모델이 시계열 데이터의 일반적인 패턴을 학습하는 데 집중할 수 있도록 하는 것이다. 이렇게 하면 모델은 이상치가 아닌 다른 정상적인 데이터 포인트들로부터 패턴을 학습하고, fine-tuning된 모델은 실제 이상치를 더 잘 감지할 수 있게 된다.

Evaluation

KPI dataset과 Yahoo dataset으로 실험을 진행했다.

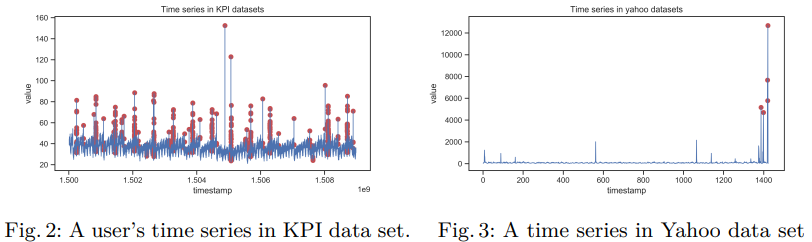
Metrics의 경우 일반적인 anomaly detection처럼 precision, recall, F1-score을 기준으로 한다. 단, 각각의 timestamp를 확인하는 것 보다는 그 연속성을 반영하여 Trun와 False를 구분한다.

Hyperparameter setting은 아래와 같다.

결과는 다른 Benchmark Model에 비해 좋은 성능을 보였다. 특히 당시 SOTA였던 SR+CNN보다 높은 성능을 보였다는 부분에서 충분한 의미가 있다고 생각한다.

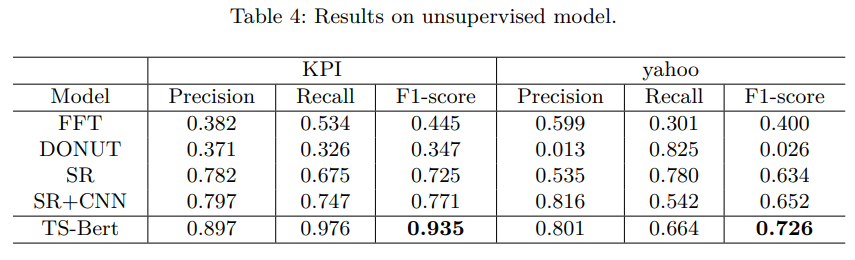
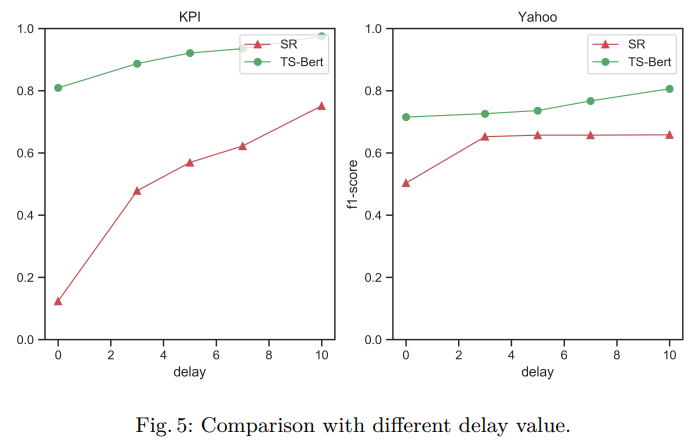
Conclusion

TS-Bert의 성능, unsupervised learning이 가능하다는 점을 강조하면서 결론을 짓는다.
하지만 해당 논문이 풀어야 하는 숙제는 상당하다는 생각이 든다. Time series anomaly의 저차원적인 data point를 Transformer의 Encoder를 거쳐 고차원 공간에 mapping시키는 행위 자체가 상당히 비효율적이라는 생각이 들 뿐더러, 학습 시간도 꽤나 오래 걸릴 것이다. 그리고 앞에서도 언급한 것 처럼 엄밀히 따진다면 unsupervised learning이라고 보기 힘들다.

그럼에도 불구하고 연구적인 측면, 성능을 올리기 위해 transformer을 사용해보는 시도를 한 측면에서 충분히 읽어볼 가치가 있다고 생각한다.