가설검정 총체적 정리(p-value만 따질게 아니다)

가설검정을 전체적으로 정리해보자

통계적 가설검정(Stastical hypothesis)은 항상 오류를 수반한다. 참/거짓을 100% 논할 수 없기 때문에 가설의 기각/채택 여부를 확률적으로 접근할 수 밖에 없다. 일반적으로 가설검정을 위한 실험 설계 시 귀무가설과 대립가설을 둔다.

H0 : negative(부정) - null hypothesis(귀무가설, 영가설)
H1 : assertion(주장) - alternative hypothesis(대립가설)

통계적 가설검정은 기존의 통념이 깨질 수 있는 새로운 가설을 제시하고자 할 때, 기존의 통념을 부정함으로써 새로운 가설을 주장하는 귀납적 접근법이라고 생각해도 될 듯 하다.

가설 검정 실험 자체는 굉장히 쉽다. R이나 Python으로 코트 한 줄이면 충분하다. 하지만 어떻게 실험을 설계하느냐, 어떻게 해석하느냐에 따라 그 결과가 천차만별로 달라질 수 있으므로 보다 개념을 확실히 알아야 할 필요가 있다.(그냥 돌려서 p값이 0.05보다 낮다고 다 통과시키다가 큰일날 수 있다는 소리이다)

<정리>

1. p-value

p-value : 귀무가설 하에, 관측된 검정 통계량을 기각시킬 때 발생하는 제 1종 오류의 최솟값(=귀무가설 하에, 극단적인 데이터가 우연히 발생할 확률)
$cdf$ : 기준 분포의 cdf. t-test에서는 정규분포의 cdf가 될 것이다.
$ts$ : 검정 통계량

• 좌측검정에서 p-value = $cdf(ts)$
• 우측검정에서 p-value = $1-cdf(ts)$
• 양측검정에서 p-value는 검정 통계량 값이 음수이냐 양수이냐에 따라 각각 "좌측검정의 p-value x 2", "우측검정의 p-value x 2"가 된다.

2. 각종 오류들

1종 오류(Type I Error) : 귀무가설이 참일 때, 이를 기각할 확률

• 좀 더 쉽게 생각해보자. 기존의 주장이 맞아서 무언가 조치를 취하지 않는 것이 좋은데 자꾸 새로운 주장이 맞다고 때쓰는 것이다.
• 유의수준(Significance Level, α) : 1종 오류를 허용할 최대 확률. 즉, 사전에 연구자가 미리 정하는 값
  -> 유의수준 α를 0.05로 설정한다는 것은 귀무가설이 참인데도 불구하고 이를 기각하는 오류를 범할 확률을 0.05로 제한한다는 의미이다. 이 상황에서 p-value가 통제된 1종 오류 값(=유의수준)보다 작은 경우 귀무가설을 신뢰할 수 없게 되는 것이다.
• 신뢰수준(Confidence Level, 1-α) : 파라미터에 대한 신뢰구간이 실제 모집단의 값과 얼마나 근접한지는 나타내는 확률

2종 오류(Type II Error) : 대립가설이 참일 때, 귀무가설을 채택할 확률

• 이를 쉽게 생각해보면, 실제로는 새로운 주장이 맞아서 새롭게 조치를 취하는 것이 좋은데 자꾸 기존의 주장이 맞다고 우기는 것이다.
• 베타(β) : 2종 오류를 범할 확률. 연구자가 직접 설정하지는 않음.
  -> β는 간접적으로 통제될 수 있다. 이는 검정력(Power)과 연결된다.
• 검정력(Power) : 대립가설이 참일 때, 이를 사실로써 결정할 확률

3. 1종 오류와 2종 오류가 trade-off인 이유가 뭘까?

굉장히 헷갈릴 수 있지만 그림을 참고하여 잘 따라오면 생각보다 쉽게 이해될 것이다.

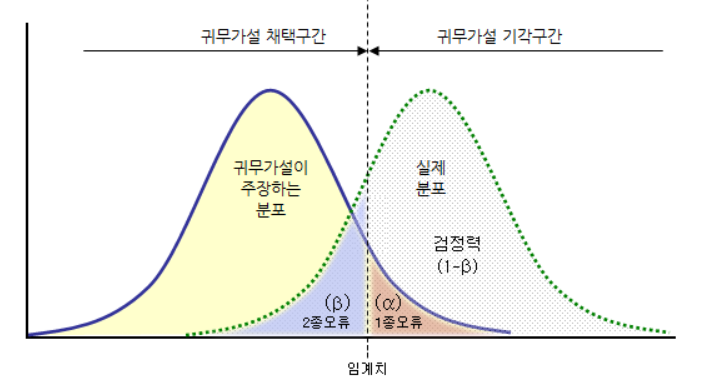
일반적으로 가설검정 시 귀무가설을 전제로 하기에 왼쪽 분포를 기준으로 진행한다. 이 때 임계치는 사전에 정하는 유의수준(연구자가 통제하는 1종 오류)에 대한 값이 된다. 실제 분포인 오른쪽 분포는 우리가 알 수는 없지만 분명 존재하며, 정해져있는 값일 것이다. 이 때 그래프 상으로 임계치를 극단으로 옮긴다면 1종오류는 감소하고, 2종오류는 증가하게 된다.

이를 좀 더 풀어서 생각하면 "검정의 임계값을 더욱 극단적인 값으로 설정하게 되어 1종오류를 범할 확률이 낮아지지만, 귀무가설을 기각하기 어려워지기 때문에(즉, 귀무가설을 채택할 확률이 높아지기에) '대립가설이 참일 경우'에 고려되는 2종오류를 범할 확률이 높아진다."라고 볼 수 있다. 대립가설이 참임에도 귀무가설을 채택할 확률인 β가 증가하는 것이다.

β의 증가는 검정력(power, 1-β)의 감소로 이어진다. 따라서 1종오류를 줄이기 위해 유의수준을 더욱 낮출 경우 대립가설이 참일 때, 이를 사실로써 결정할 확률이 줄어들게 된다.

상황에 따라 1종오류가 중요한 경우도 있고, 2종오류가 중요한 경우가 있다. 그럴 때마다 이 둘의 trade-off 관계를 잘 고려해서 실험을 설계해야 할 것이다.

예시로 의료계에서는 1종오류를 일으킬 확률을 매우 낮게 주는 경우가 많다. 연구자가 내린 결론이 잘못되었을 가능성을 매우 줄이기 위해서이다. 여기서 연구자가 내린 결론은 대립가설(H1)일 것이고, 1종오류를 일으킬 확률을 낮게 한다는 것은 귀무가설(H0)이 맞는데 잘못 기각할 확률을 낮추는 것이기에 대립가설(H1)을 잘못 채택할 확률을 낮춘다와 같은 의미가 된다.

4. 1종오류를 통제한 상황에서 검정력을 높이는 방법은 뭘까?

2종오류(β)는 검정력(Power, 1-β)과 정확히 반비례 관계이다. 따라서 1종오류가 증가하면, 즉 신뢰수준이 나빠진다면 검정력은 좋아진다. 좀 더 풀어서 생각해보면, 신뢰수준이 낮아지면 유의수준은 올라가고 귀무가설을 기각하기가 쉬워지기 때문에 검정력이 높아지는 것이다.

그러나 2종오류를 줄이기 위해(=검정력을 높이기 위해) 무작정 1종오류를 늘리는 행위는 좋지 않다.

검정력과 연관이 있는 다른 지표들이 있을까?

1. 효과 크기(Effect Size)가 높으면 검정력(Power)이 올라간다.

• 효과 크기는 두 그룹 간의 차이 또는 연구에서 발견된 효과의 크기를 의미한다. 이는 평균차이가 될 수도, 상관계수가 될 수도 있으며, Cohen's d와 같이 차이를 표준화한 지표를 활용할 수도 있다.
• 효과 크기가 클 수록 검정력이 높아지는 이유는 효과 크기가 크게 나타날 경우 통계적 검정에서 이를 발견하기가 더 쉽기 때문이다.

2. 표본 크기(n)을 높이면 검정력(Power)이 올라간다.

• 표본 크기를 높이면 표본 평균의 변동성이 줄어들고, 실제 효과를 더 명확히 감지할 수 있게 된다. 표준 오차가 줄어들기에 검정 통계량의 값이 커지게 되고, 이는 귀무가설을 기각할 가능성이 높아진다. 이는 실제로 대립가설이 참일 때, 이를 발견하고 귀무가설을 기각할 확률이 높다는 의미이다. 즉, 검정력이 높아지는 것과 같은 맥락이다.

5. 표본 크기를 늘릴 때 주의할 점

물론 실험 조건 등을 개선해서 더 큰 효과를 꽤할 수 있지만, 이를 고려하지 않는 경우 유의수준(α)를 고정한다는 가정하에 표본 크기를 늘림으로써 검정력(Power)를 높일 수 있다. 이는 또한 모집단에 가까워지기에 결과의 신뢰성을 높여줄 것이다.

하지만 표본 크기(n)은 데이터를 얻기 전 미리 설계해두는 것이 좋을 수 있다. 실험 결과를 바탕으로 원하는 결과가 안나왔다는 이유로 n을 늘리면 p-hacking으로 이어질 수 있기 때문이다.

표본 크기(n)이 높아질수록 p-value는 낮아진다. 그 이유는 표본 크기(n)의 증가는 표본 평균의 표준 오차($s/√n$)를 감소시키고, 결과적으로 검정 통계량을 증가시킬 수 있기 때문이다. 이렇듯 n이 높아지면 통계적 유의성을 확보하기는 쉬울 것이다. 그렇다면 n이 정말 높을 때 귀무가설을 기각하면 의미가 있다고 할 수 있을까?

사전에 표본 크기(n)을 따로 설정하지 않고 가지고 있는 데이터를 그대로 사용할 경우 n의 크기가 크다면 귀무가설을 기각해도 과연 의미가 있는 결과인지 의심해봐야 한다. 이 때 효과 크기(Effect size)를 통해 그 효과 혹은 차이가 의미가 있는지 확인할 수 있다. 즉, p-value(통계적 유의성)과 효과 크기(Effect size, 실질적 중요성)을 동시에 따져야 한다.

또한, 사전에 적절한 표본 크기(n)를 설정하는 방법도 있다. 적절한 표본 크기(n)은 α, 1−β, 효과 크기(delta)를 통해 얻을 수 있다.

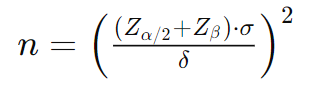
즉, 유의수준과 검정력, 효과 크기의 범위를 설정하면 n을 구할 수 있고, 이를 바탕으로 가설 검정을 진행할 수 있는 것이다.