06_01_Introduction: Probability and Statistics
- 통계 항목에서는 여러 종류의 그래프를 읽는 법을 배운다
- 또한 평균, 백분율, 표준편차, 데이터 분포 등을 배운다
- 확률 항목에서는 게임 내에서 일어나는 여러 확률적 행동에 대해서 배운다
- 또한 독립/종속 시행, 이론/경험적 확률, 확률에 관한 심리학적 이론 등을 배운다
06_02_Exploring Data
- 게임 개발자에게 데이터의 정리 및 분석은 중요하다. 게임의 문제점을 특정하고 유저 경험을 최적화한다.
- 일반적으로 정리되지 않은 데이터는 읽기 매우 힘들다. 데이터는 다음과 같이 정리할 수 있다.
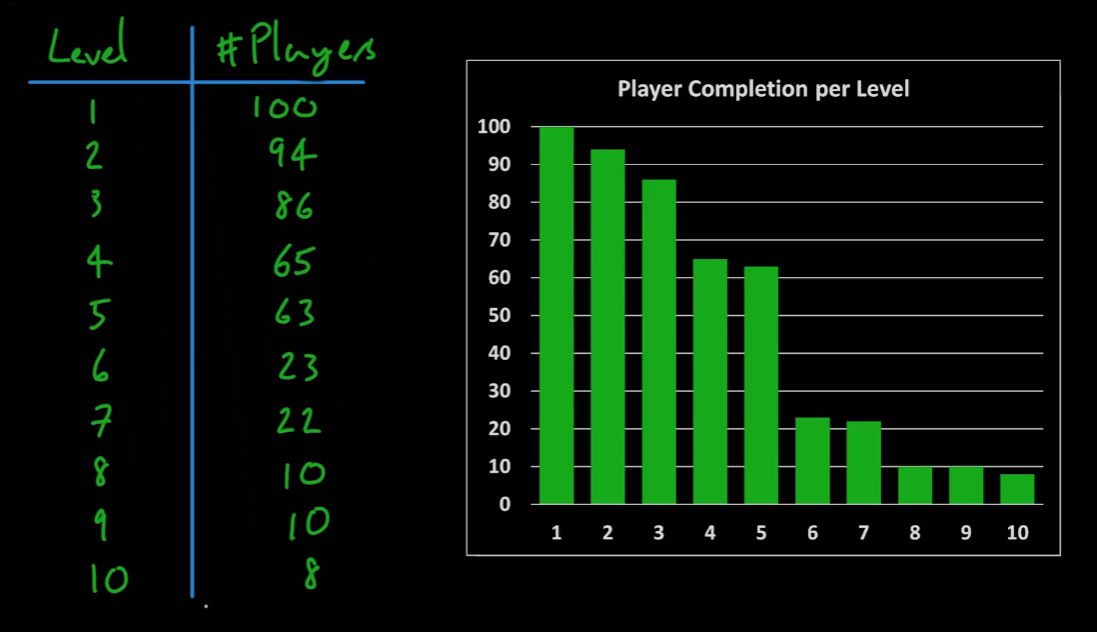
- 특정 조건에 대한 발생 빈도에 따른 표를 만든다.(얼만큼의 플레이어가 어느 레벨까지 깼는가 등)
- 많은 조건을 갖고 있을 시에는 표보다 그래프가 더 가독성이 좋다.
- 이렇게 정리되어 읽기 쉬운 데이터들은 잠재적인 문제들을 더 쉽게 특정해낼 수 있다
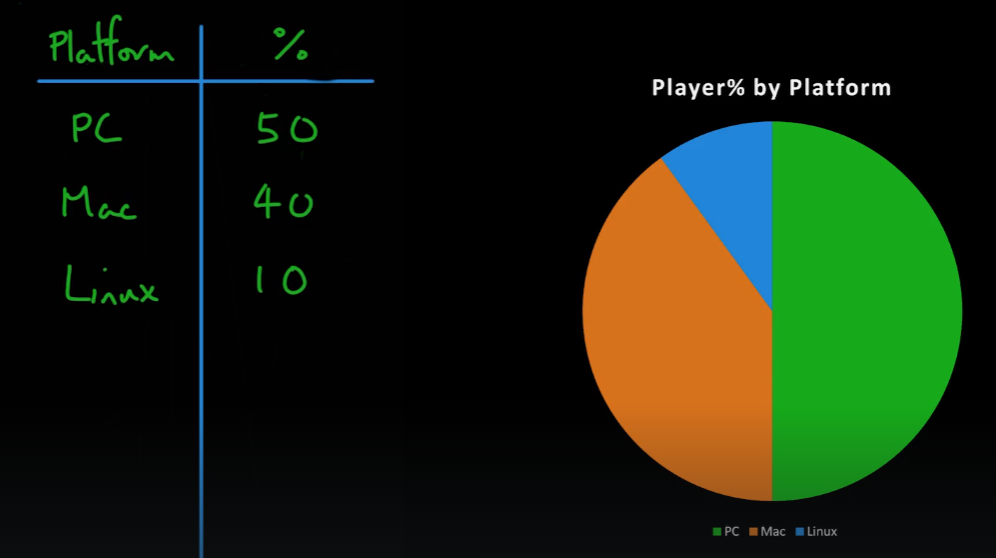
- 여러 조건이 온전히 독립적인 상황에서는 원형 차트를 사용하는 것이 가독성이 좋다.
- 그래프는 수의 가독성을 위한 장치이므로 3D 그래프 모듈처럼 가독성을 떨어뜨리는 템플릿은 지양한다
06_03_Percentages
- 퍼센트(%)는 어떤 수가 총량이 100일 때 얼만큼에 해당하는지를 뜻한다
1% = 1 / 100 = 0.01,120% = 120 / 100 = 1.20- 40원의 20%는
40 * 20 / 100 = 8원
- 백분율은 비교 등에 용이하게 사용한다
06_04_Sigma Notation
- 시그마 표기법은 급수를 계산할 때 사용하며 다음과 같이 작성한다
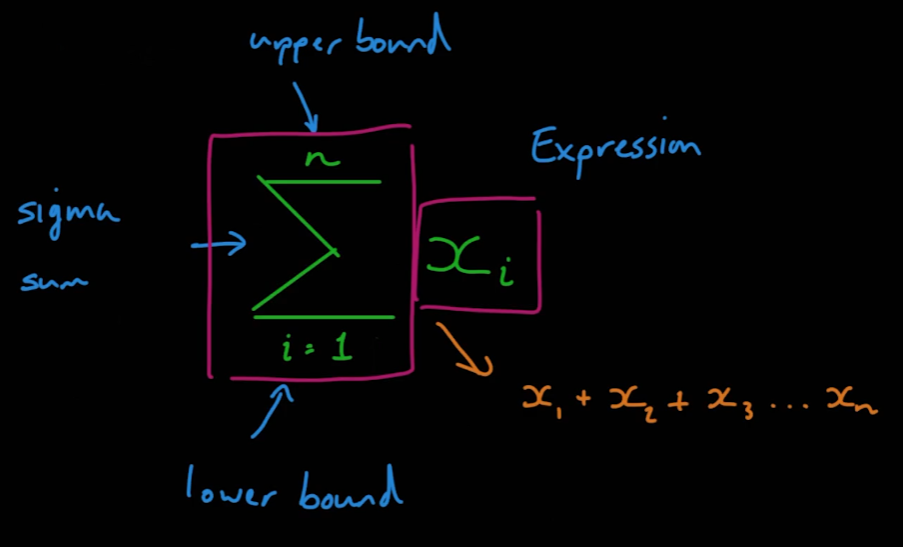
- 시그마 표기 사용 예시
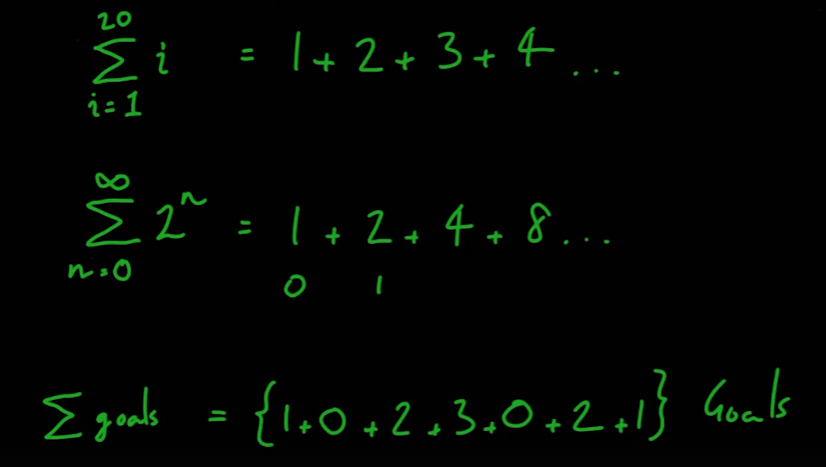
06_05_Averages
- 평균(Average)은 세 가지 종류가 있다
- 평균값(Mean) : 가장 일반적인 평균값, 모든 수를 더한 다음 총 개수로 나눈 것
- 중앙값(Median) : 정렬된 수들의 정 가운데 위치에 있는 값
- 최빈값(Mode) : 평균 혹은 중앙값을 낼 수 없는 상태에서 가장 많이 발생한 수를 나타냄

06_06_Outliers
- 관측된 데이터의 범위에서 많이 벗어난 데이터를 뜻힌다.
- 이상치를 대처할 때에 일반적으로 세 가지 방법이 사용된다. 상황에 따라 적절한 방법을 사용한다
- 무시 : 해당 데이터를 보관하지만 분석할 때는 사용하지 않는다
- 삭제 : 해당 데이터를 삭제한다
- 조정 : 해당 데이터의 값을 정상 범위 내로 조정한다
06_07_Skewness
-
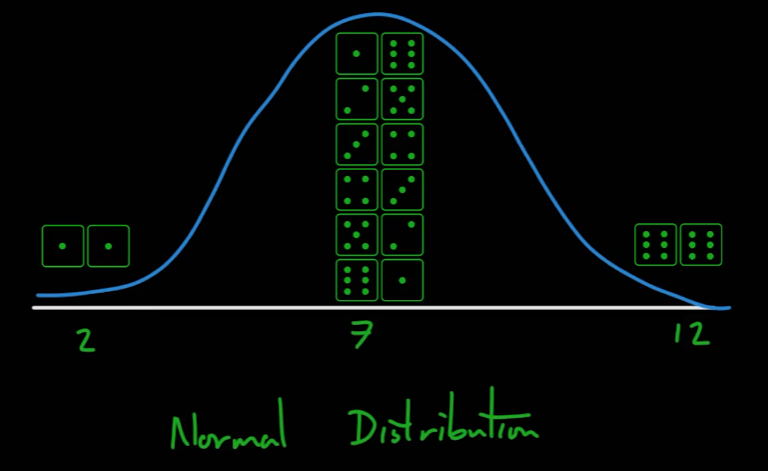
다수의 확률이 정규 분포를 따르게 된다.
- 아래의 사진의 경우 평균값, 중앙값, 최빈값이 모두 동일한 값이 된다.
- 하지만 모든 데이터가 이러한 이상적인 분포를 가질 순 없다
-
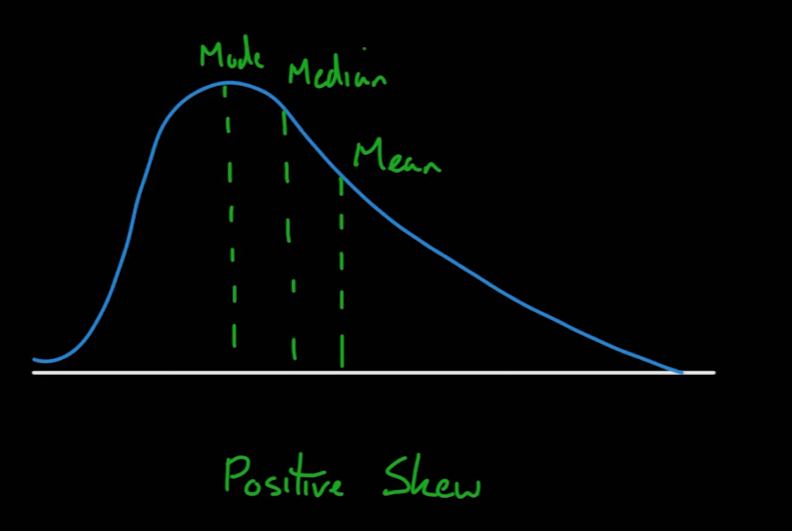
오른쪽 꼬리 분포(Right/Positive Scew)
- 대체적으로 평균 > 중앙값 > 최빈값을 띈다
- 대체적으로 평균 > 중앙값 > 최빈값을 띈다
-
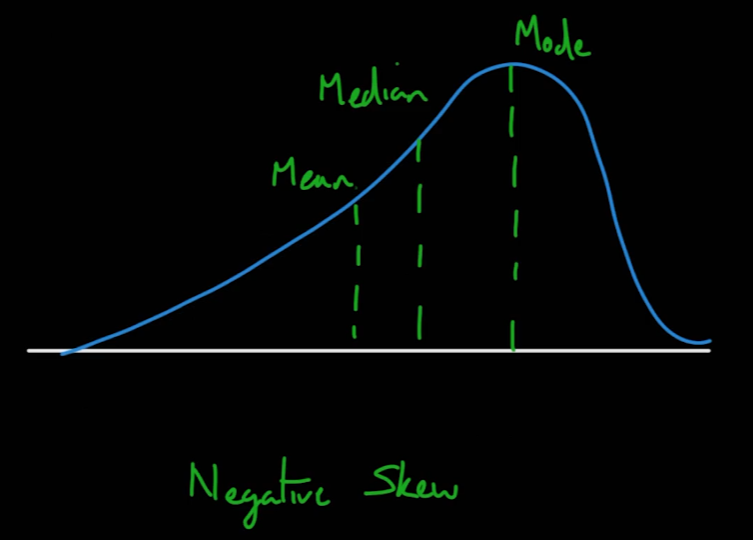
왼쪽 꼬리 분포(Left/Negative Scew)
- 대체적으로 평균 < 중앙값 < 최빈값을 띈다
- 대체적으로 평균 < 중앙값 < 최빈값을 띈다
06_08_Interquartile Range
- 사분 편차로 데이터의 분산과 비대칭도를 특정하기 쉽다.
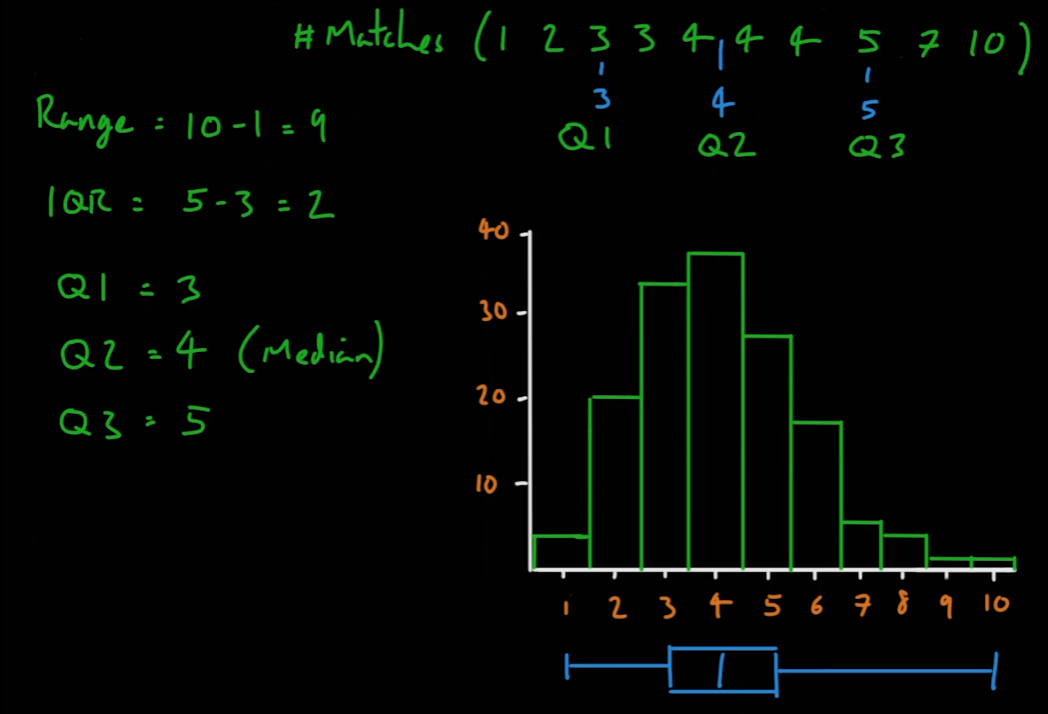
06_09_Standard Deviation
- 자료의 관찰값들이 얼마나 흩어져 있는지에 대한 척도이다
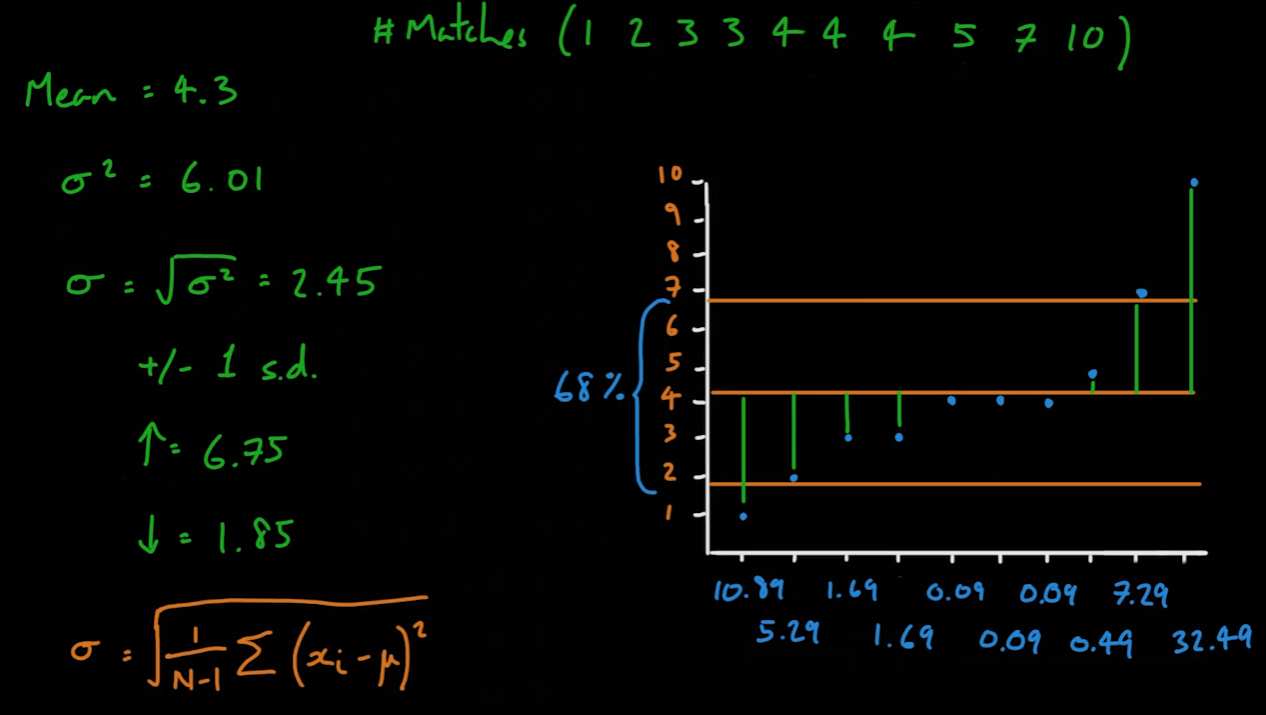
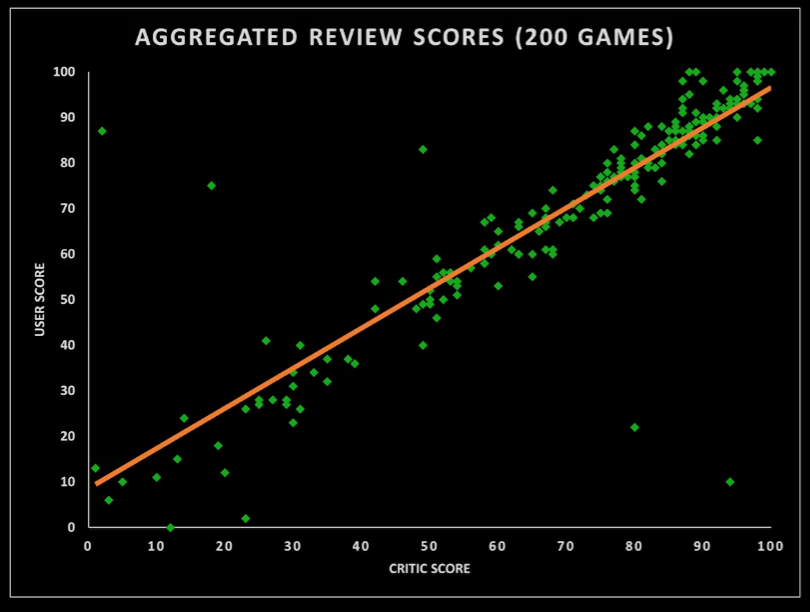
06_10_Correlation
-
데이터간 관계를 나타낼 때 사용한다
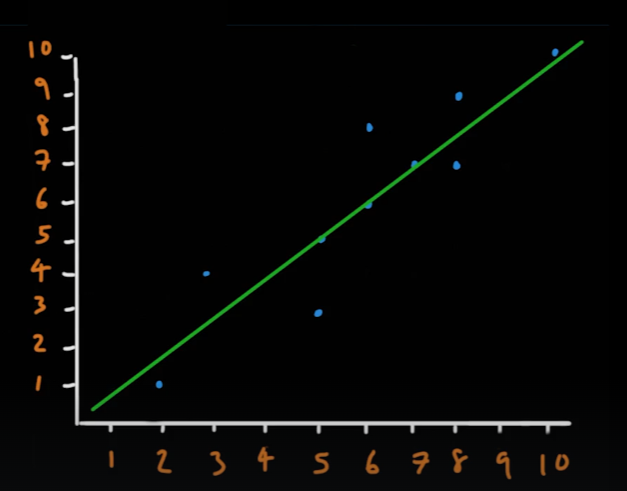
-
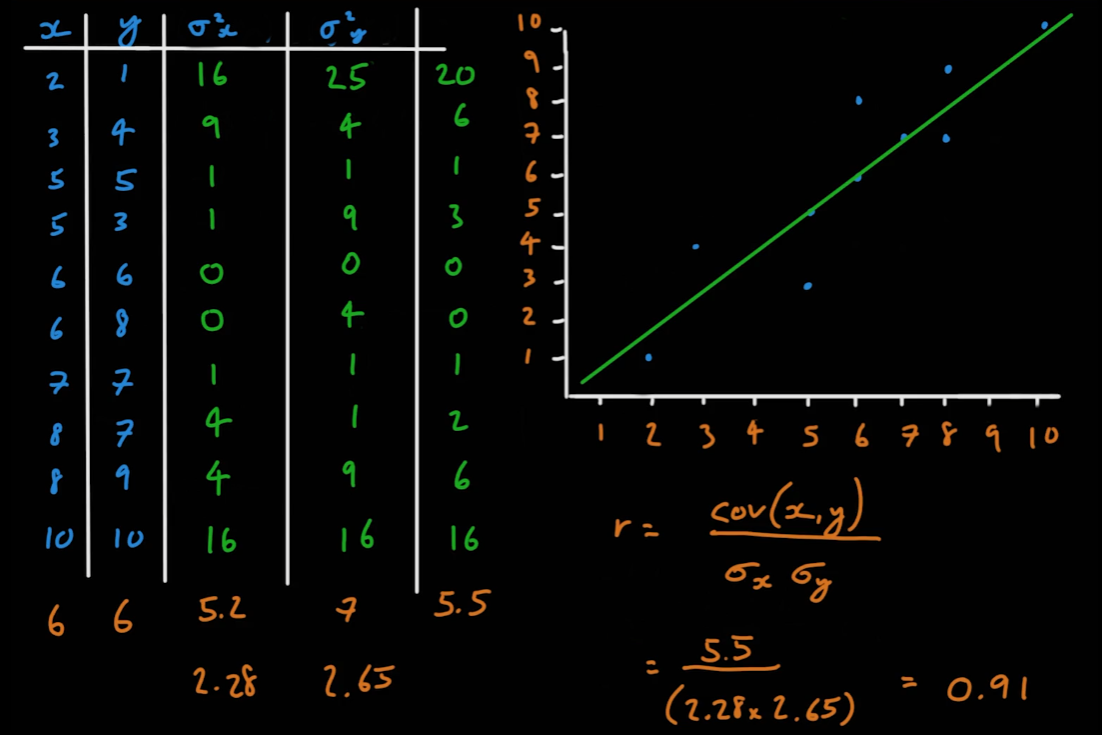
상관관계값(r)은 -1 이상 1 이하의 값을 갖는다.
- r = 1일 시 모든 데이터는 완벽한 양의 상관관계를 갖는다.(모든 데이터 좌표가 양의 1차방정식 그래프 위에 존재)
- r = -1일 시 모든 데이터는 완벽한 음의 상관관계를 갖는다.(모든 데이터 좌표가 음의 1차방정식 그래프 위에 존재)
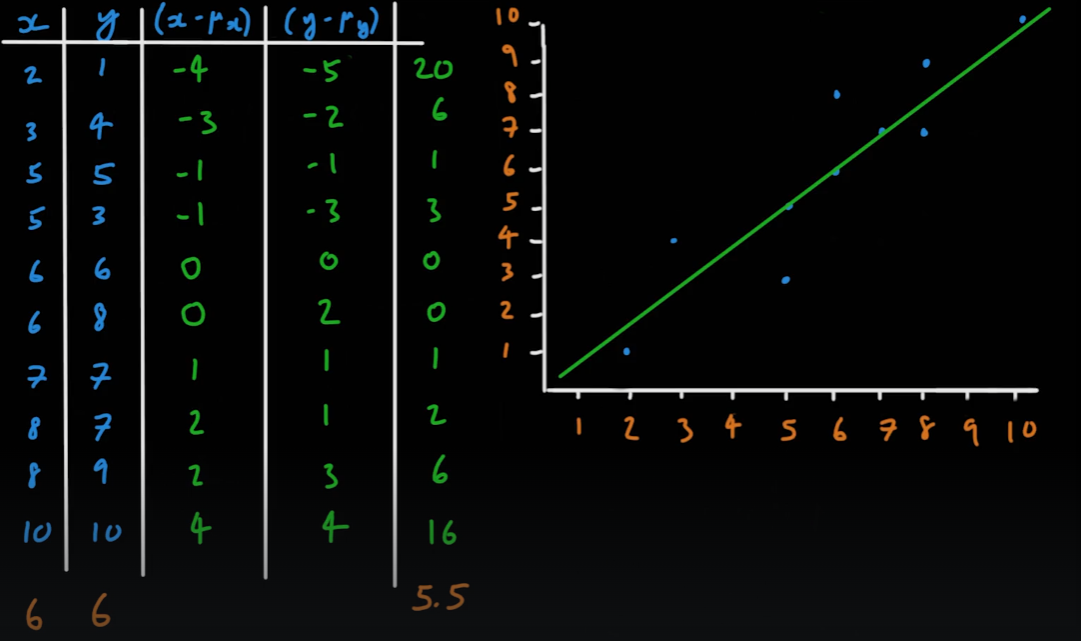
-
상관관계값 r을 아는 방법은 다음과 같다
- 모든 점의 좌표를 x와 y로 분리한다.
- 각각의 x와 y의 값을 각각 x의 평균과 y의 평균으로 뺀 값을 구한다.
- 2번에서 나온 값들을 같은 점의 x와 y끼리 곱하여 모두 더한 후 평균을 구한다.
- 2번에서 나온 값들을 각각 제곱한 후 그 값들의 평균을 구한 후 제곱근을 얻는다.
- r값은 3번의 값을 4번의 x값과 y값을 곱한 값을 나누어 구한다
06_11_Causation
- 위의 그림에서 인과관계는 다음과 같이 나타낼 수 있다
- 크리틱 점수가 유저 점수에게 영향을 준다
- 유저 점수가 크리틱 점수에 영향을 준다
- 유저와 크리틱 점수 둘다 다른 요인에 의해 영향을 받는다
- 또한 이러한 인과관계도 존재한다
- 먹잇감과 포식자의 개체수는 둘 다 서로에게 영향을 받는다
- 치즈 소비량과 공학 전공자의 수는 서로에게 형향이 없다
06_12_Normalizing Data
- 데이터의 총량(스케일)이 다른 두 그래프간에 비교하기 편하게 하기 위해 사용한다
- 각 데이터의 정규화는 다음과 같이 실시한다
- 정규값을 0~1이 아닌 다른 범위로 하고 싶으면 최소값과 범위를 이용해 값을 변경할 수 있다
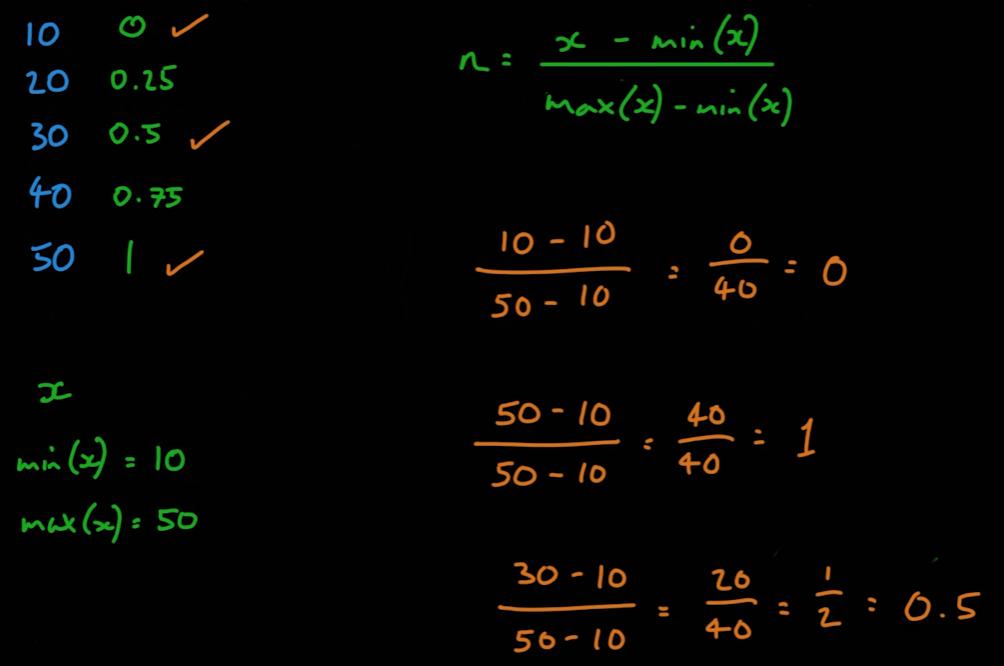
- 정규값을 0~1이 아닌 다른 범위로 하고 싶으면 최소값과 범위를 이용해 값을 변경할 수 있다
06_13_Probability 101
- 확률이라 함은 어떠한 일이 발생할 가능성의 척도이며, 대체로 백분율 혹은 0~1의 정규값을 통해 나타낸다
- 보통 확률은
원하는 일이 발생한 경우의 수 / 모든 일이 발생한 경우의 수이다

06_14_Consecutive Events
- 어떠한 확률이 연속해서 발생할 확률은 그 확률끼리 곱하여 표현한다.
- 주사위 2개가 6, 6으로 나올 확률은
(1 / 6) * (1 / 6) = (1 / 36)이다 - 카드덱에서 카드 두 개를 뽑아 둘 다 에이스가 나올 확률과 둘 중 하나가 에이스가 나올 확률은 다음과 같이 도출할 수 있다.
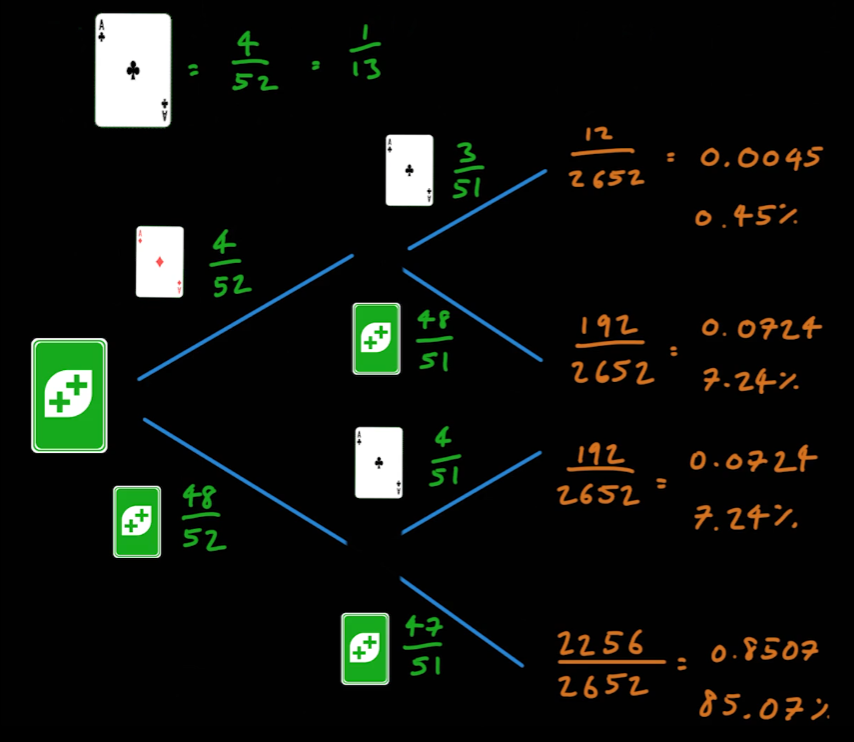
- 주사위 2개가 6, 6으로 나올 확률은
06_15_Complement Rule
- 확률 실험에서 모든 가능한 사건의 확률의 총합은 1이어야 한다는 규칙
06_16_Theoretical vs Experimental
- 실험적 확률은 실험의 총 횟수가 커질수록 이론적 확률과 비슷해진다.
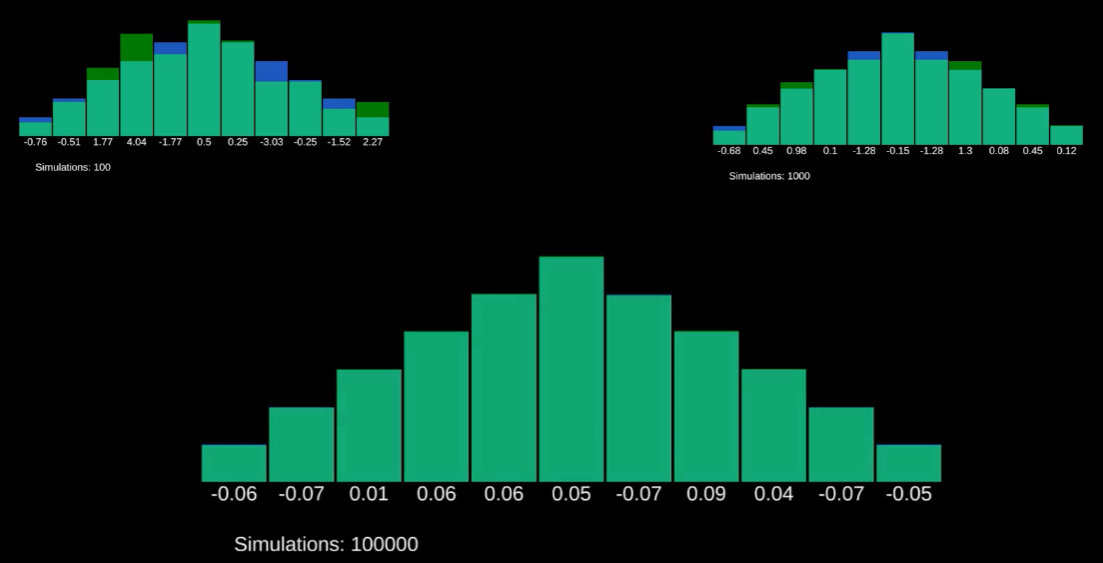
- 만일 실제 확률이 이론적 확률과 많이 다른 경우 해당 확률을 담당하는 코드 스크립트에 오류가 존재할 가능성이 있다
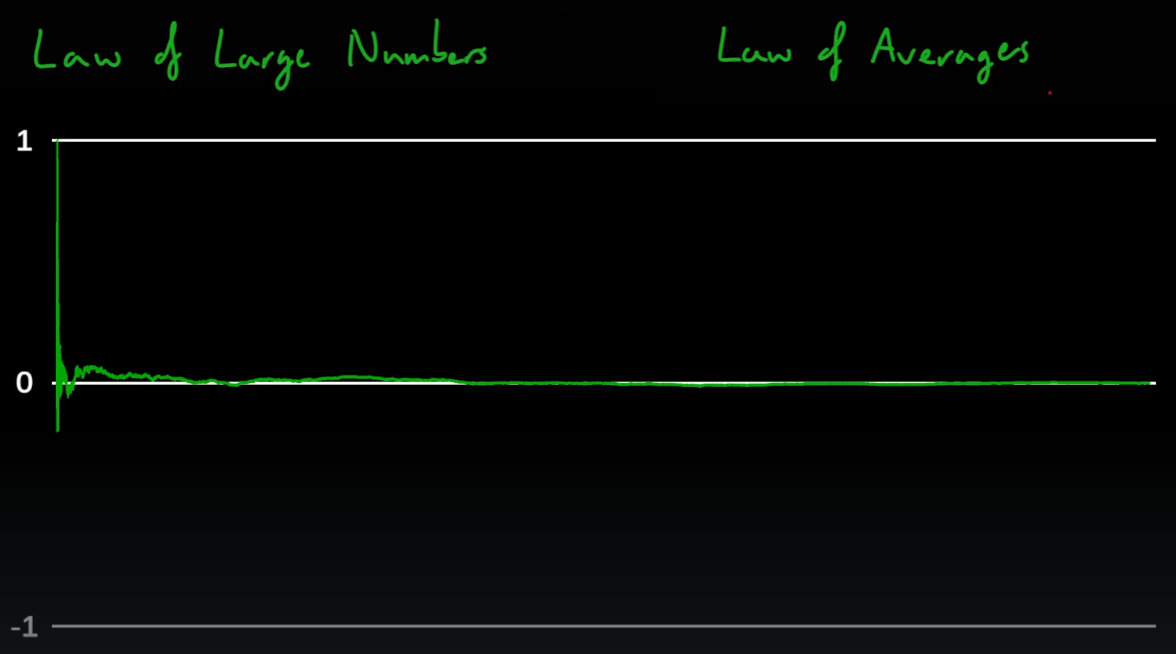
06_17_The Law of Averages
- 확률적 행위는 횟수가 거듭될수록 평균에 가까워진다는 법칙이다
06_18_Bayes' Theorem
- 베이즈 정리를 이용해 해결할 수 있는 몬티 홀 문제
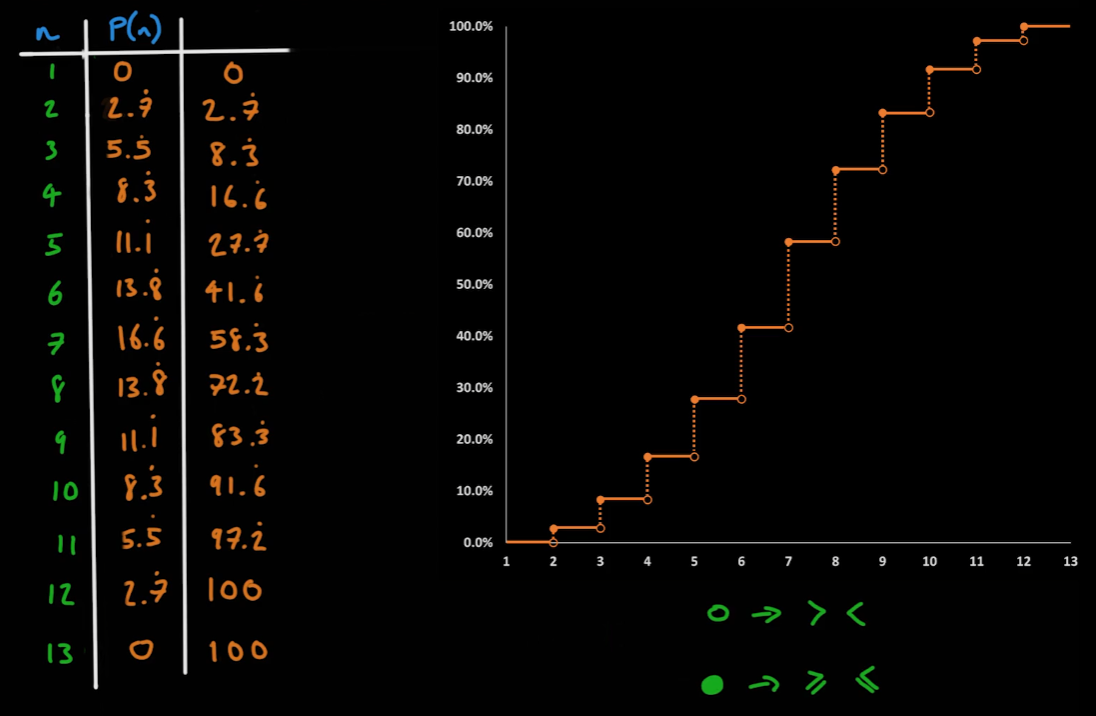
06_19_Cumulative Distribution Function
- 각각의 확률을 더해가면서 만드는 그래프
06_20_Elo Rating System
- 멀티플레이 게임에서 플레이어들간의 실력을 판정하는 방법
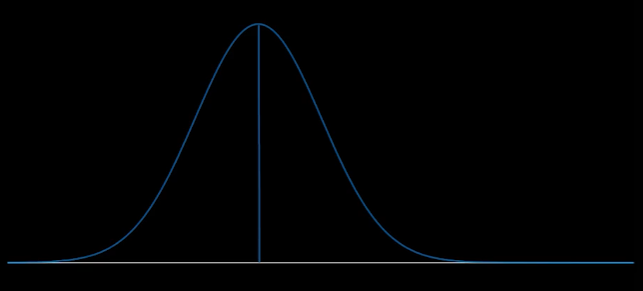
- 다음 그림은 한 플레이어의 실력 그래프이다
- 플레이어는 여러 요인에 따라 평균보다 실력이 높을수도, 낮을수도 있다
- 가운데 그어진 선이 플레이어 실력의 평균이며, 이것이 바로 ELO 점수이다
- A플레이어와 B플레이어의 ELO점수에 대한 실력 그래프는 다음과 같다.
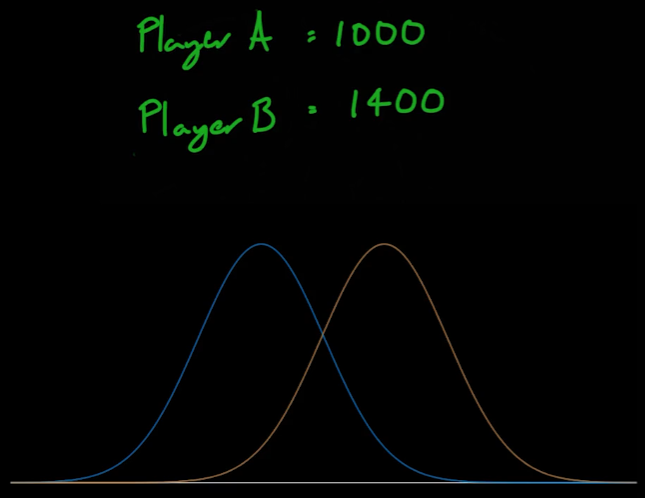
- A가 승리 시 ELO점수의 변화가 크게 나타나고, B가 승리시 ELO점수의 변화가 적게 나타나는 기술을 구현하기 위해 로지스틱 함수를 사용한다
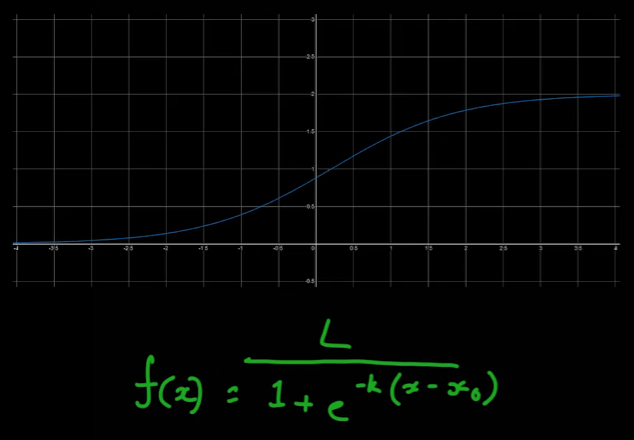
- L값을 바꾸면 최댓값을, k값을 바꾸면 기울기, x0값을 바꾸면 그래프의 중간점의 위치를 변화시킬 수 있다.
- 위의 공식을 다음과 같이 바꾼다.
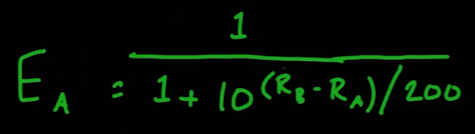
- RA, RB는 각각 플레이어 A, 플레이어 B의 점수이다
- 이 때 200의 의미는
두 플레이어가 200점이 차이가 날 시 승률이 10배 차이가 나고, 400점이 차이가 날 시 승률이 100배 차이가 난다는 의미
- 경기 종료 후 ELO값의 변동은 다음과 같이 할 수 있다.
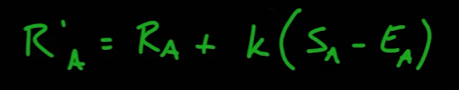
- SA는 실제 스코어, EA는 예상 스코어(위에서 계산한 승률)이다
- K는 추가할 점수에 대한 일반적인 가중치이다. (SA - EA)가 일반적으로 -1에서 1 사이의 값이므로 플레이어에게 변화값을 좀 더 잘 보여주기 위해 추가하는 값이다
- 점수차에 따른 기대 승률과 추가할 점수에 대한 가중치는 개발자의 재량 혹은 여러 실험적 측정을 통해 정해나간다.
- 또한 모든 플레이어의 실력 편차가 다르므로 이에 대한 보정도 추가로 해 주어야 한다.