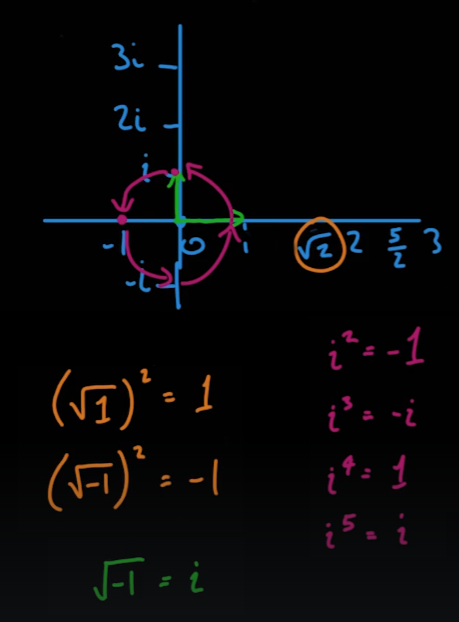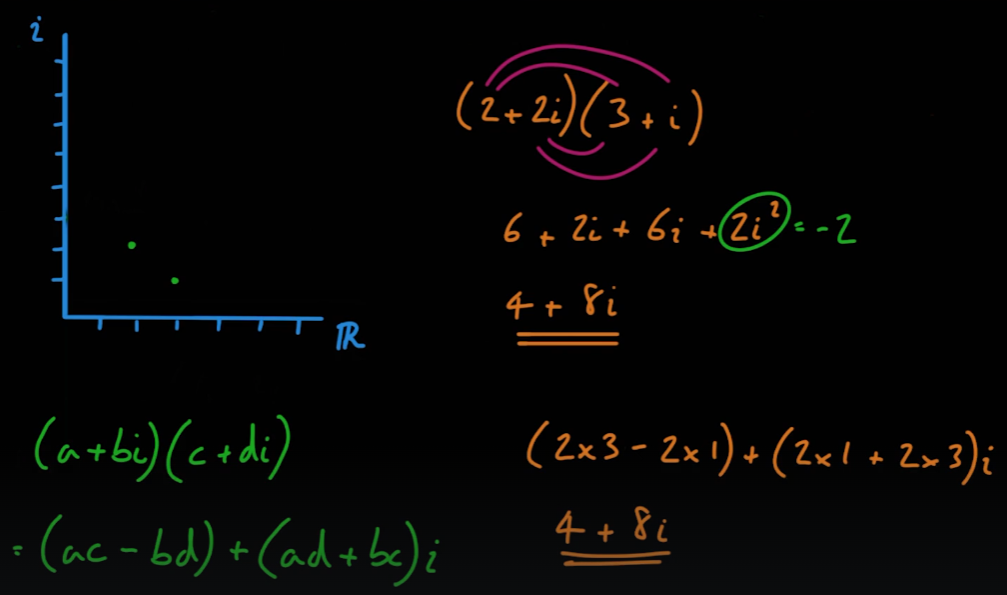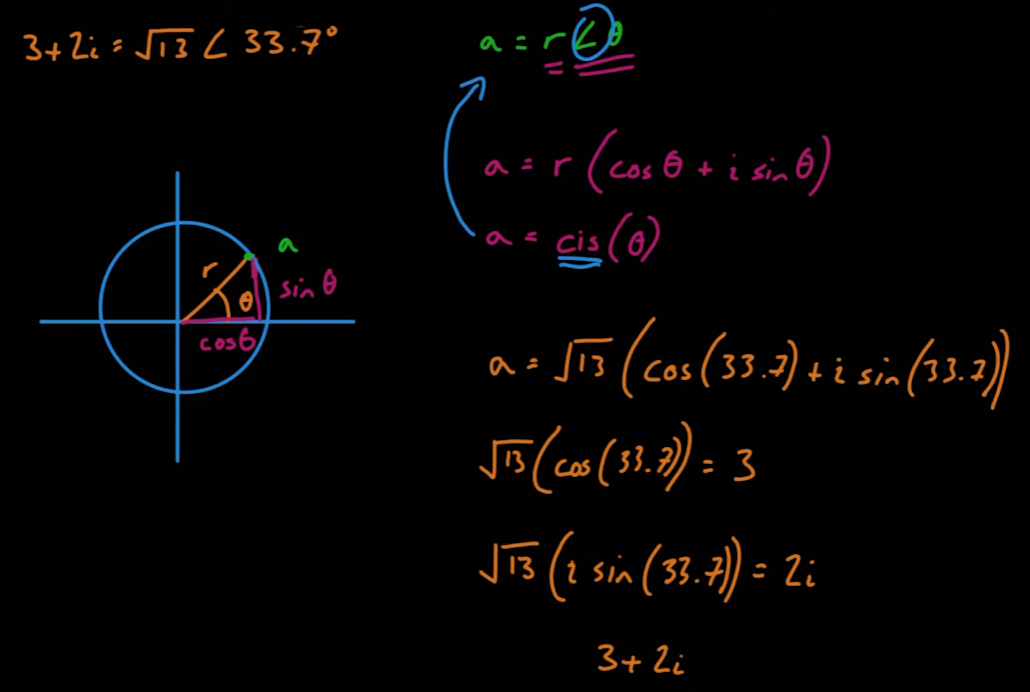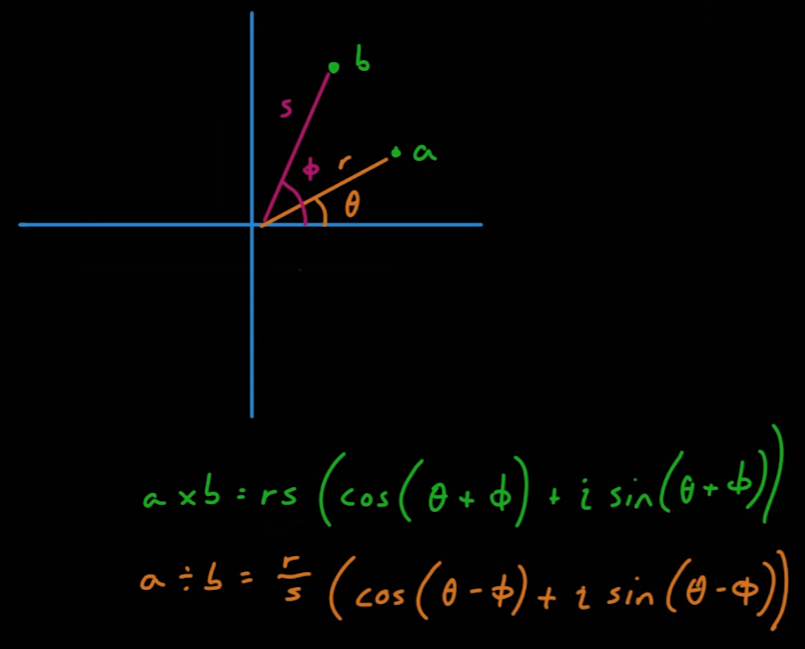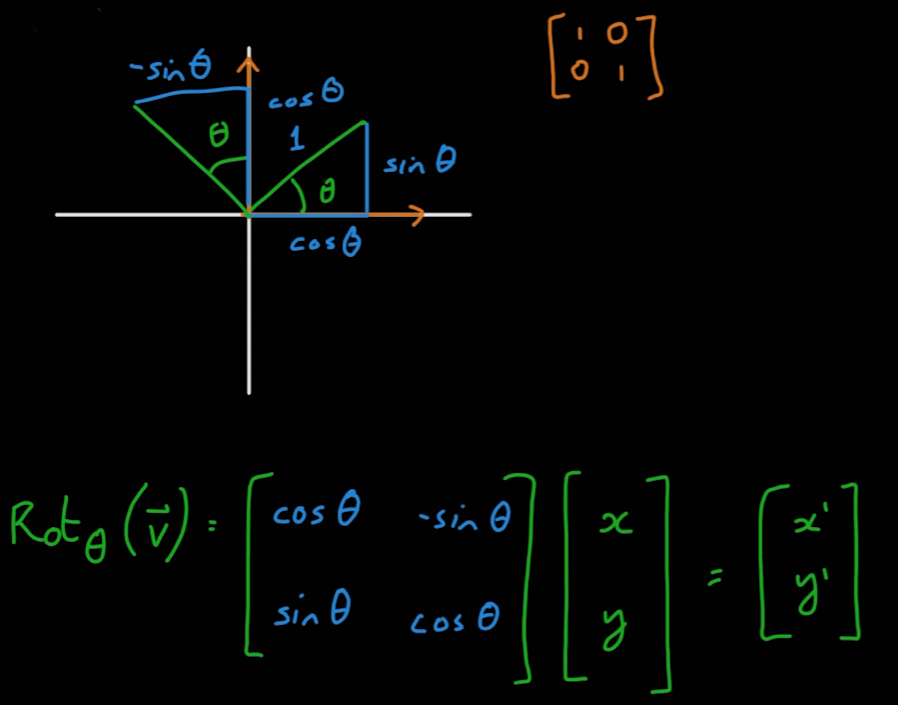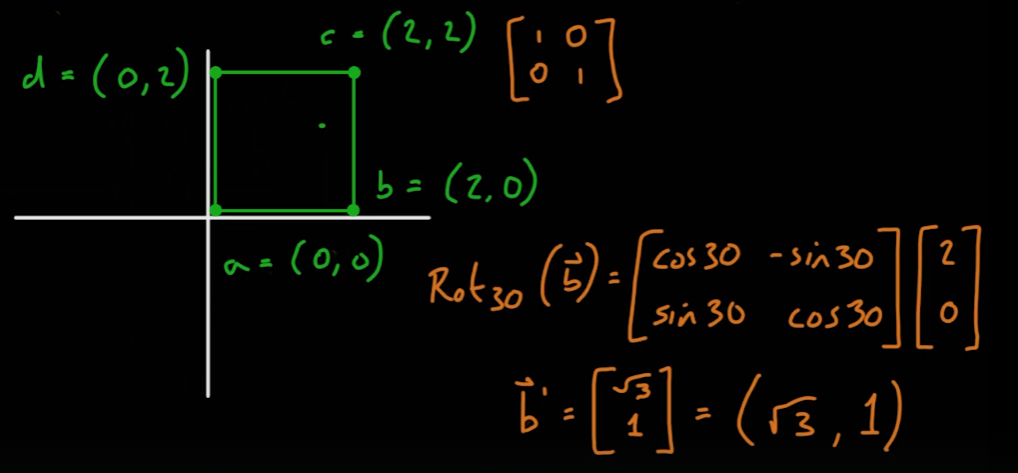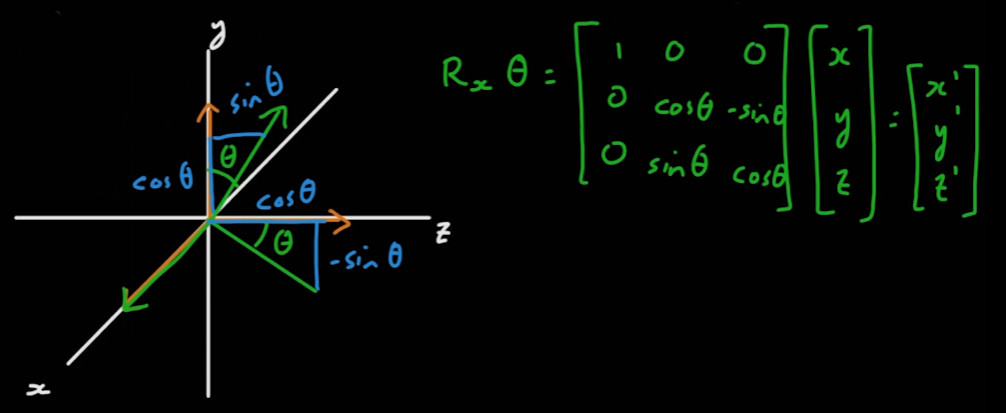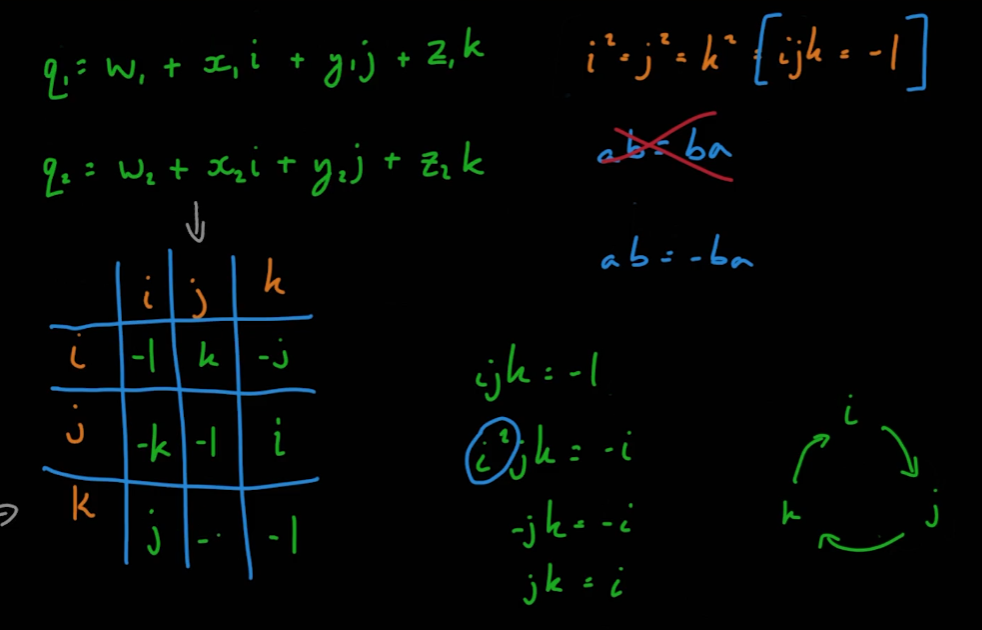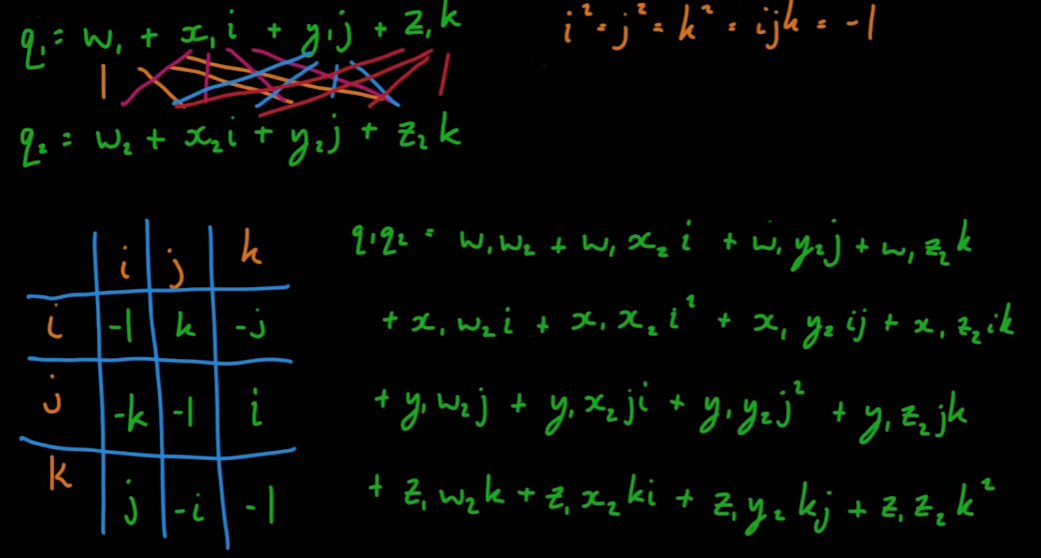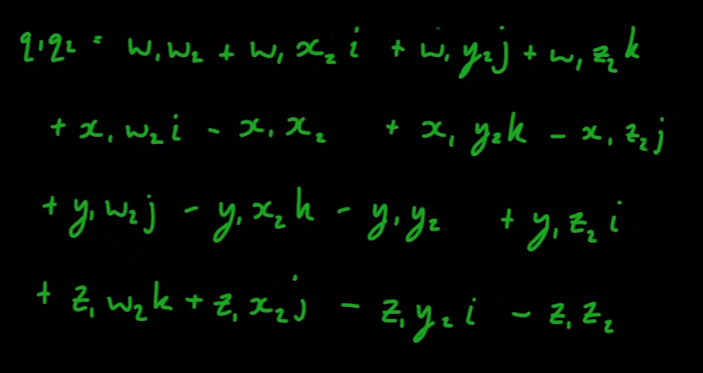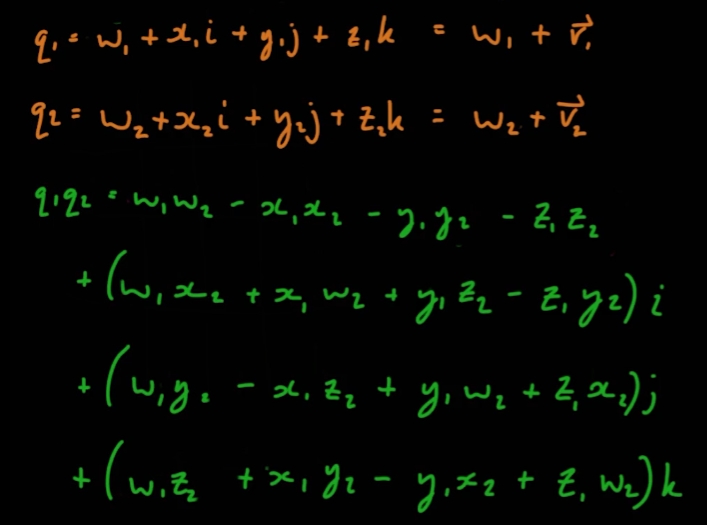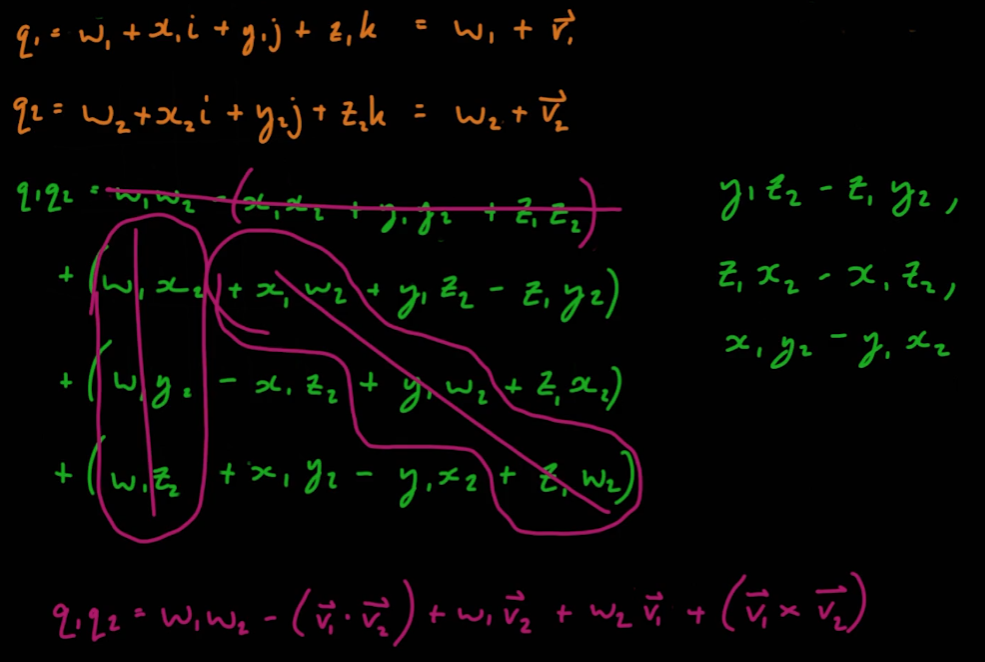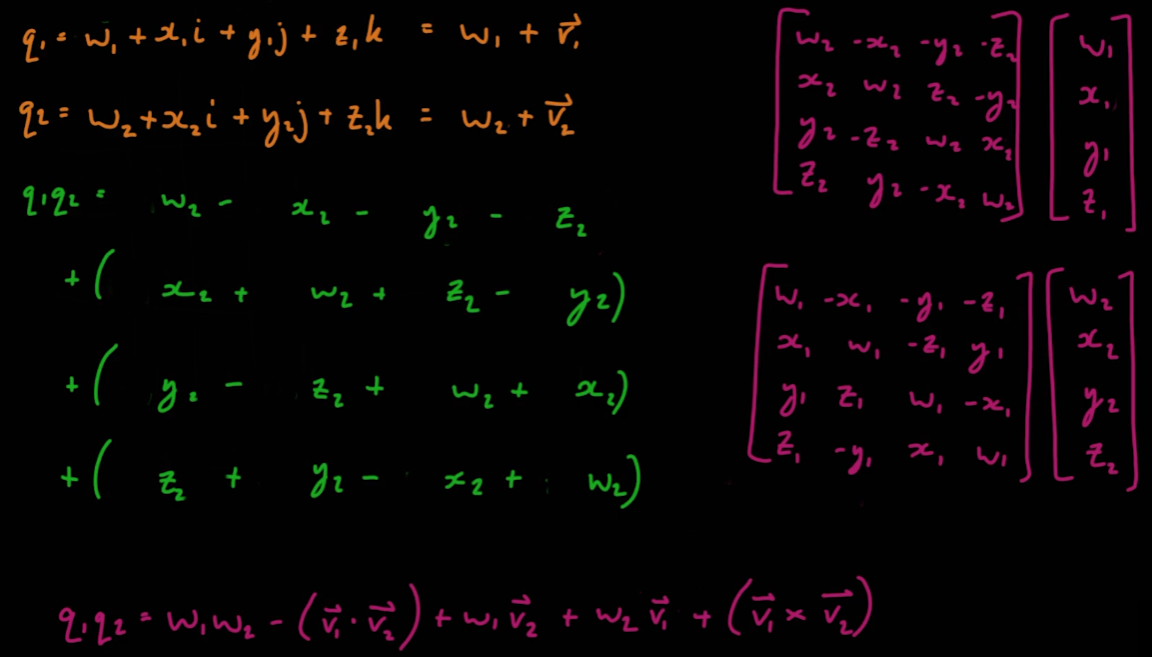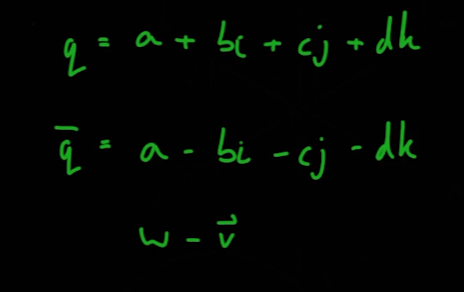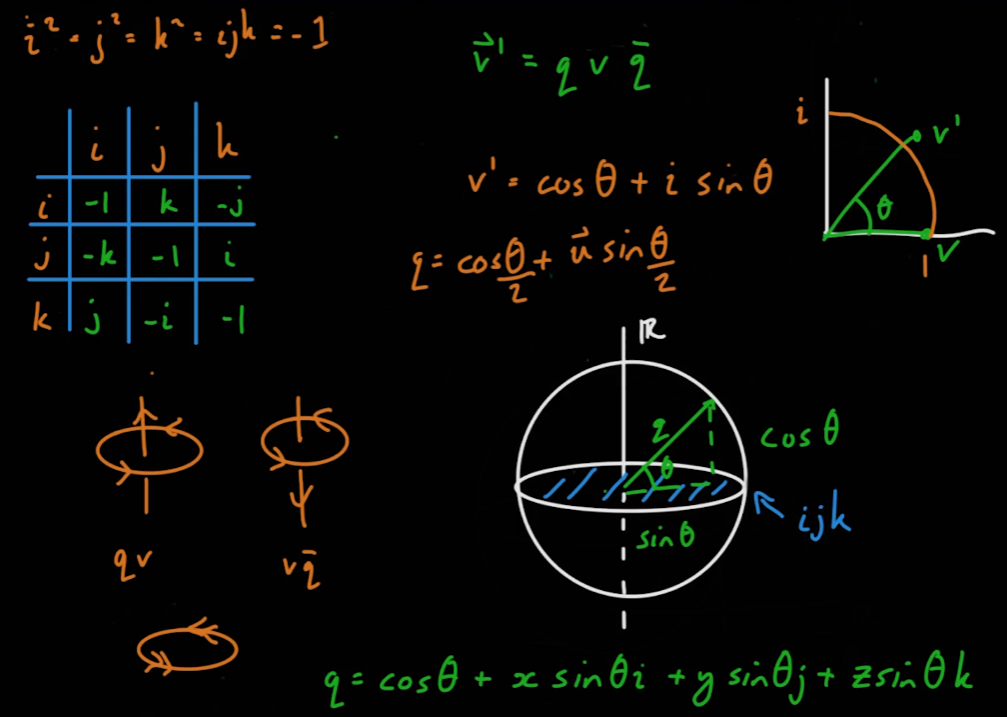게임 수학 - 회전과 보간

05_01_Introduction: Rotation and Interpolation

• 이번 챕터에서는 오일러 각도와 쿼터니언, 그리고 보간에 대해 공부한다

05_02_Vector Direction

• 벡터의 방향을 좌표상의 각도로 나타낼 수 있다.
• 이차원 벡터의 방향각은 다음과 같이 계산할 수 있다.
  
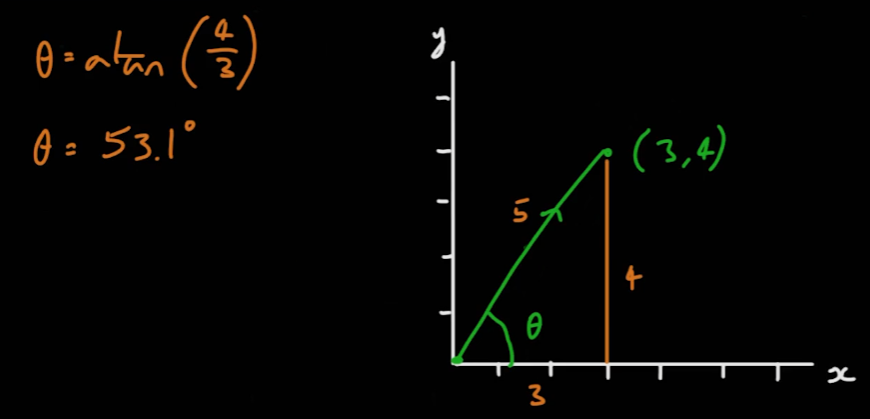
• 삼차원 벡터의 방향각은 다음과 같이 계산할 수 있다.
  
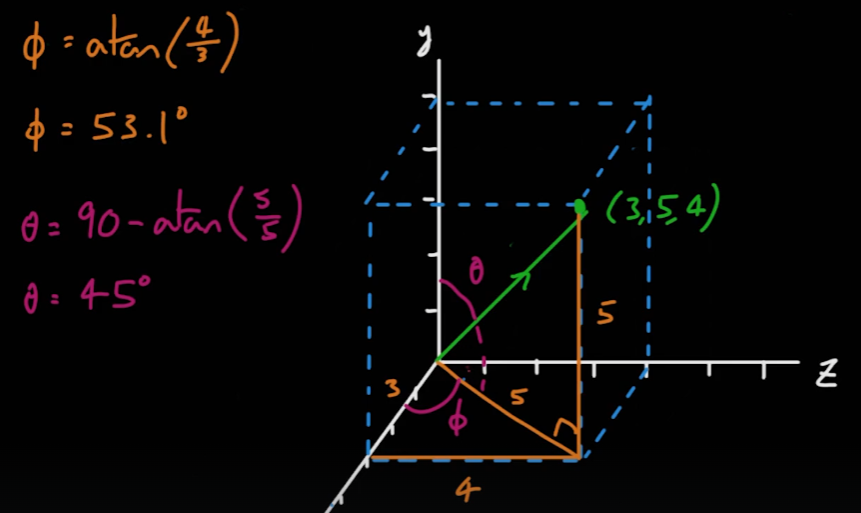
• 위의 방법은 방향각은 구할 수 있으나 하나의 좌표축에만 연관되어 있다. 세 좌표축 모두와 연관된 방향각은 다음과 같이 구할 수 있다.
  

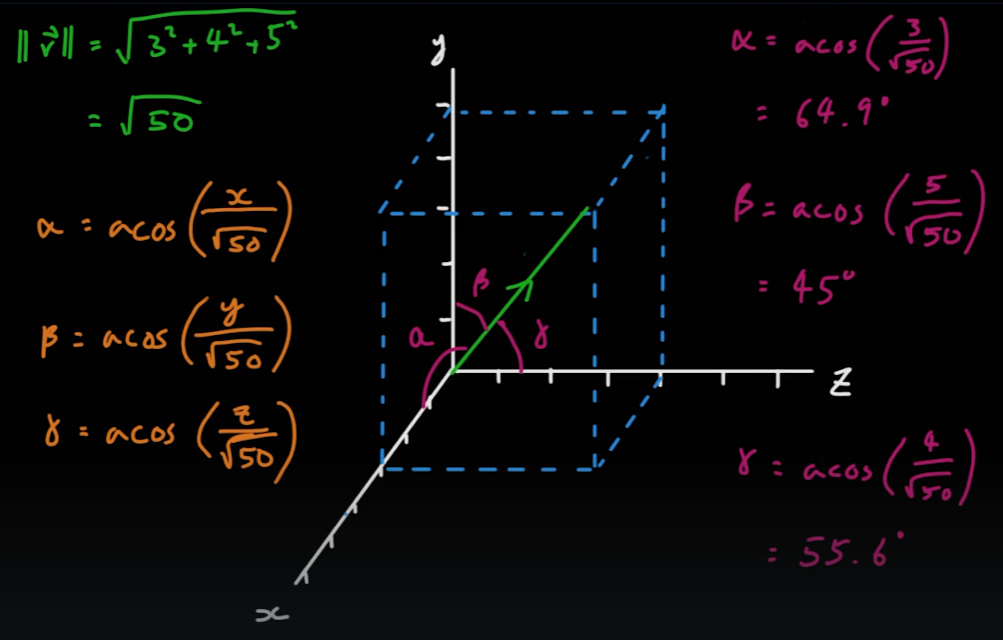
05_03_Imaginary Numbers

위키피디아-허수

• 이차원 복소수 좌표 내에서 허수를 이용해 회전을 할 수 있다.
  

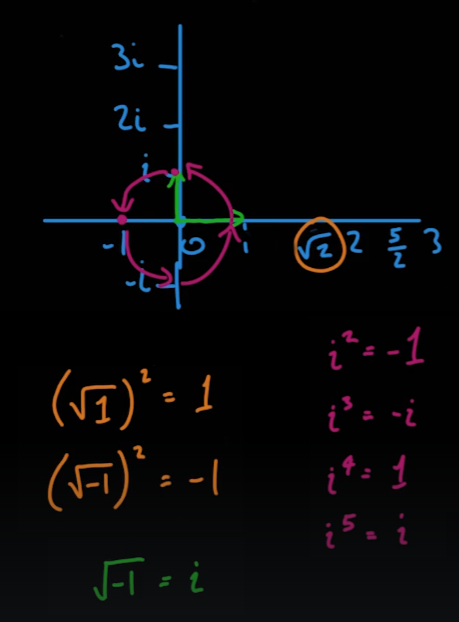
05_04_Complex Numbers

위키피디아-복소수

• 복소수들은 실수와 허수가 각각의 축을 담당하는 이차원 복소수 좌표로 나타낼 수 있다.
• 복소수를 이용해 쿼터니언을 구현할 수 있다.
• 복소수의 합은 실수부와 허수부를 각각 합한 값이다
  

05_05_Complex Multiplication

• 복소수들의 곱은 기본적으로 이차방정식처럼 구할 수 있다.
  
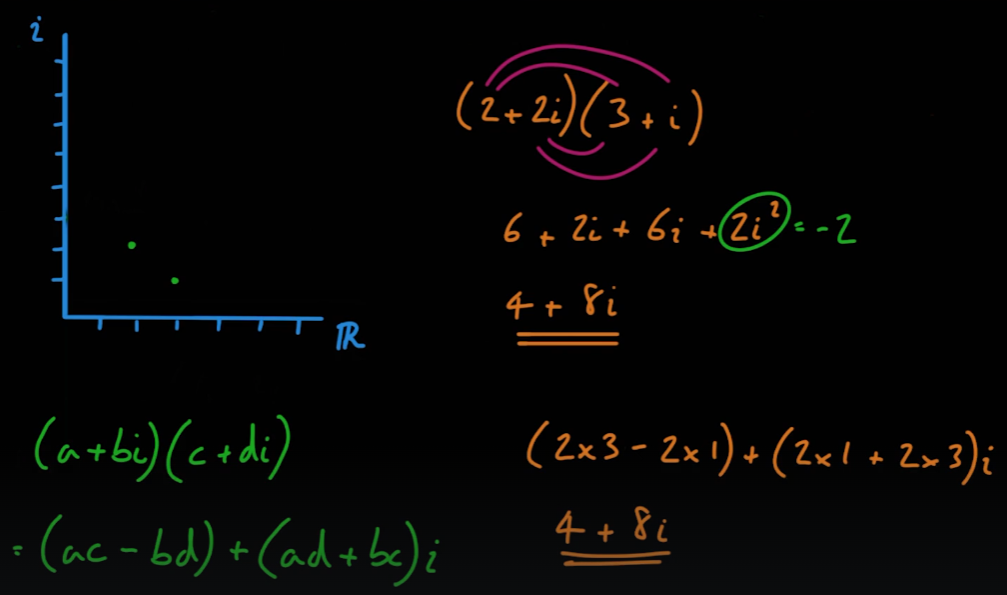
• 또한 복소수들의 곱은 복소수 좌표계에서 두 좌표의 벡터 방향각의 합과 벡터 길이의 곱이다
  • 극좌표계 참조
    

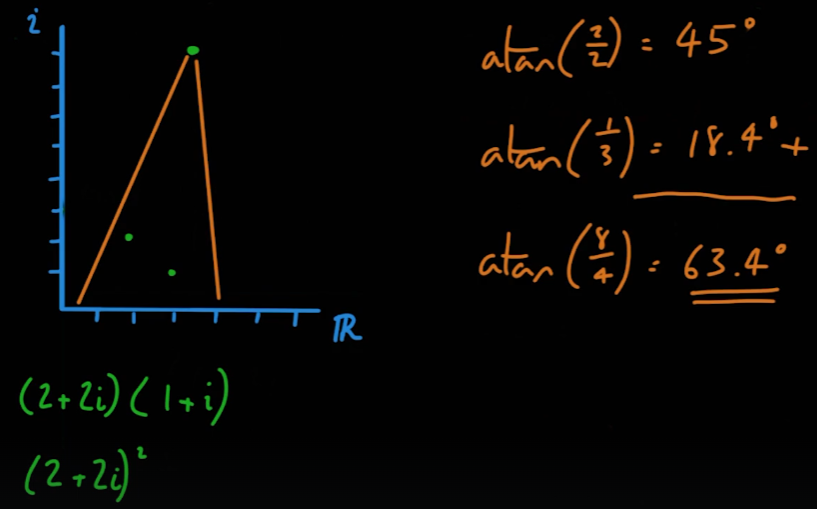
05_06_Polar Coordinates

위키피디아-극좌표계

• 복소수 3+2i는 다음과 같이 나타낼 수 있다.
  
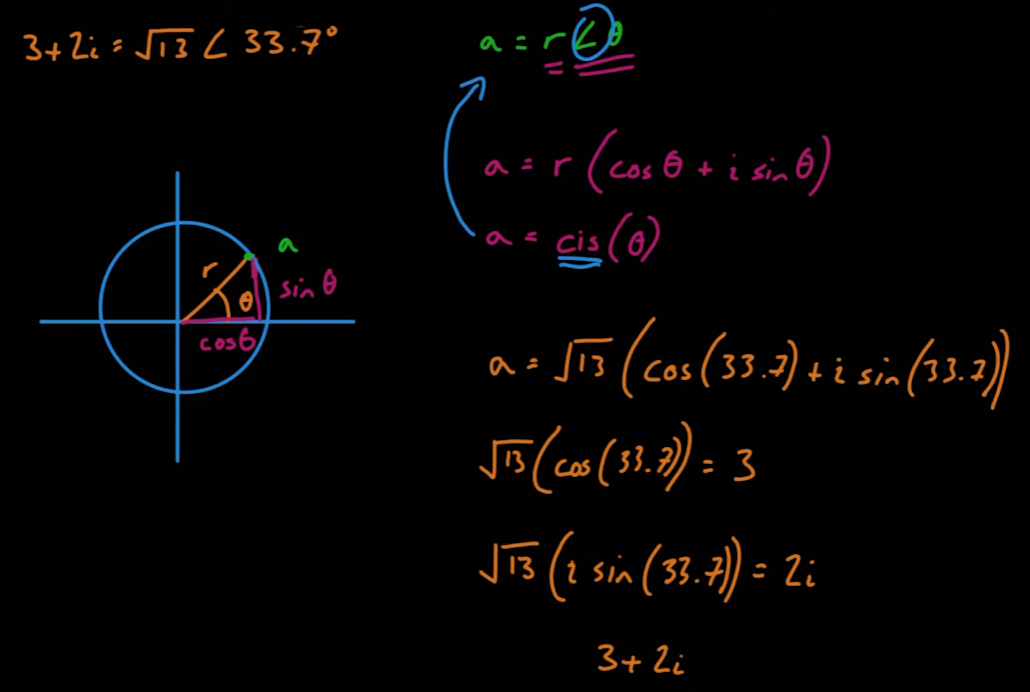
• 따라서 복소수의 곱셈과 나눗셈은 다음과 같이 유도할 수 있다.
  

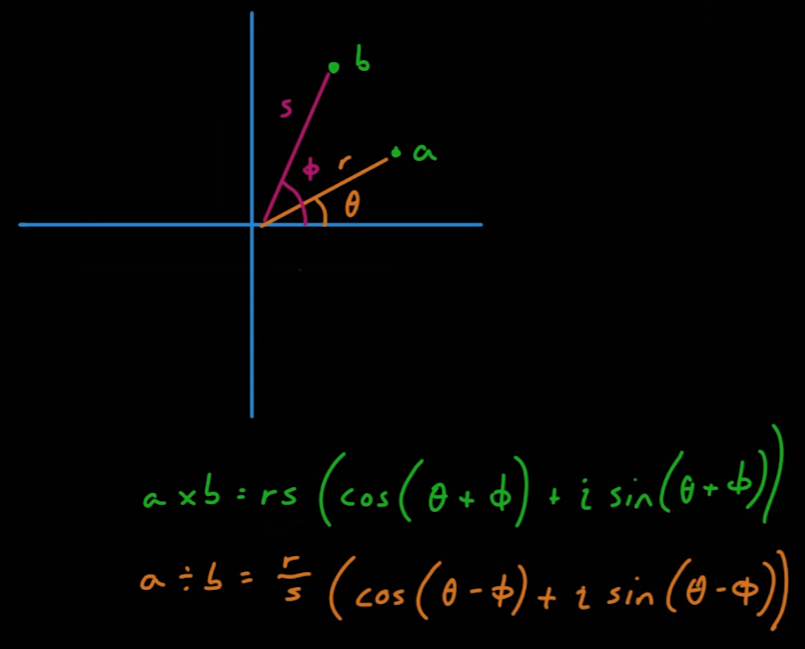
05_07_Rotation Matrix

• 극좌표계와 행렬을 이용해 회전 행렬을 만들 수 있다.
• 회전 행렬은 회전의 저장과 사용이 매우 편리하다.
• 이차원 좌표에서의 회전 행렬은 다음과 같이 유도 및 사용된다.
  
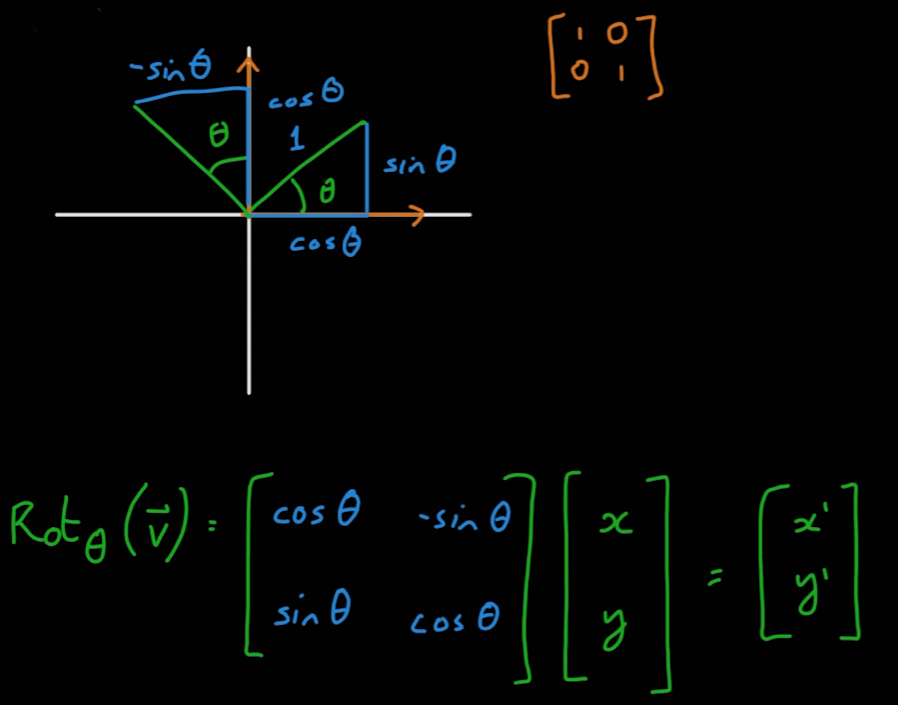
• 이차원 좌표에서의 회전 벡터 사용 예시
  

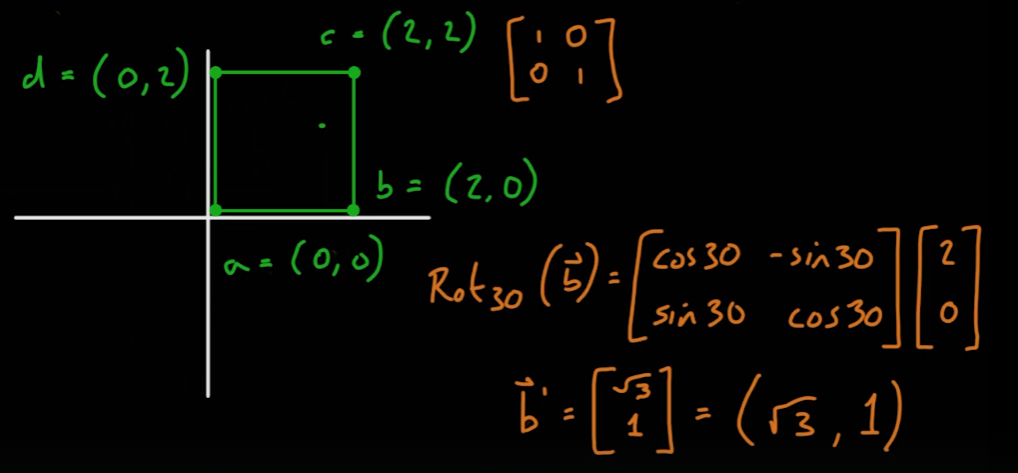
05_08_Euler Rotation

• 위에서 행한 좌표계의 회전을 3차원으로 확장하면 오일러 회전이 된다
• 오일러 회전에서의 회전각은 롤(x축), 요(y축), 피치(z축)로 구성되어 있다
  
• 3차원 좌표가 x축을 중심으로 세타만큼 회전했을 때의 회전 행렬은 다음과 같이 유도된다.
  
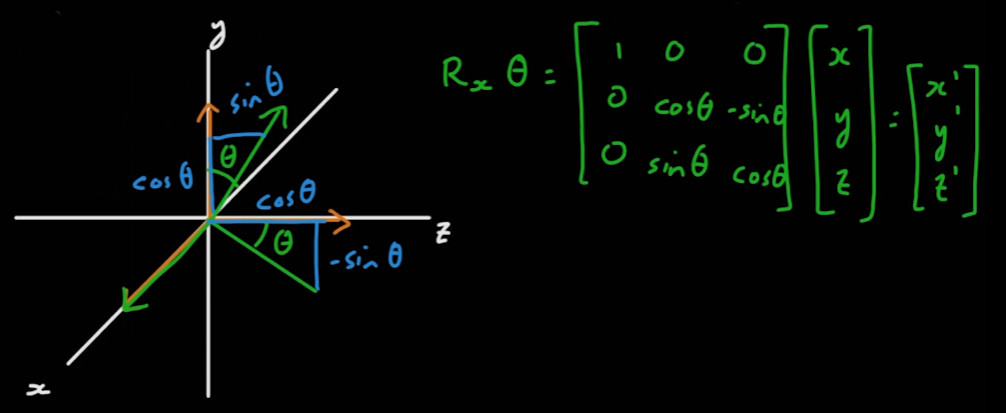
• 3차원 좌표가 각각 x, y, z축을 중심으로 세타만큼 회전했을 때의 회전 행렬은 다음과 같이 나온다.
  
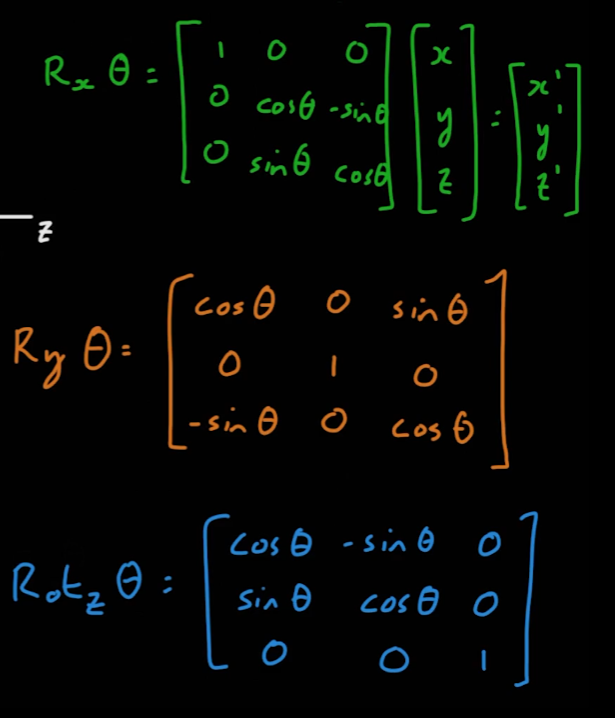
• 오일러 회전에서 회전축의 계산 순서는 중요하다.

05_09_Gimbal Lock

• 두 개의 축이 맞물려버려 두 축이 하나의 방향으로 회전시킬 때 짐벌락에 걸렸다고 한다
  
• 오브젝트의 회전축 계산 순서를 조정하거나, 가장 사용하지 않는 각도를 찾아 조정하는 것으로 짐벌락을 어느 정도 회피할 수 있다. 하지만 오일러 각도를 사용하면 짐벌락 문제를 완전히 회피할 수 없다

05_10_What are Quaternions?

간단 요약

• 복소수를 사용해 2D좌표상에서 방향과 회전을 파악하던 것처럼(a + bi) 3D좌표상에서의 방향과 회전을 파악할 때(a + bi + cj + dk) 사용한다. 이를 쿼터니언이라 한다
  • 이는 4차원 좌표상에서 나타나는 점이 된다
  • b, c, d가 모두 0이면 실수부 a만 남게 된다
  • i, j, k를 축으로 하는 3차원 점 (b, c, d)를 만들게 될 시 쿼터니언 q는 a + (bi, cj, dk)가 된다.
    

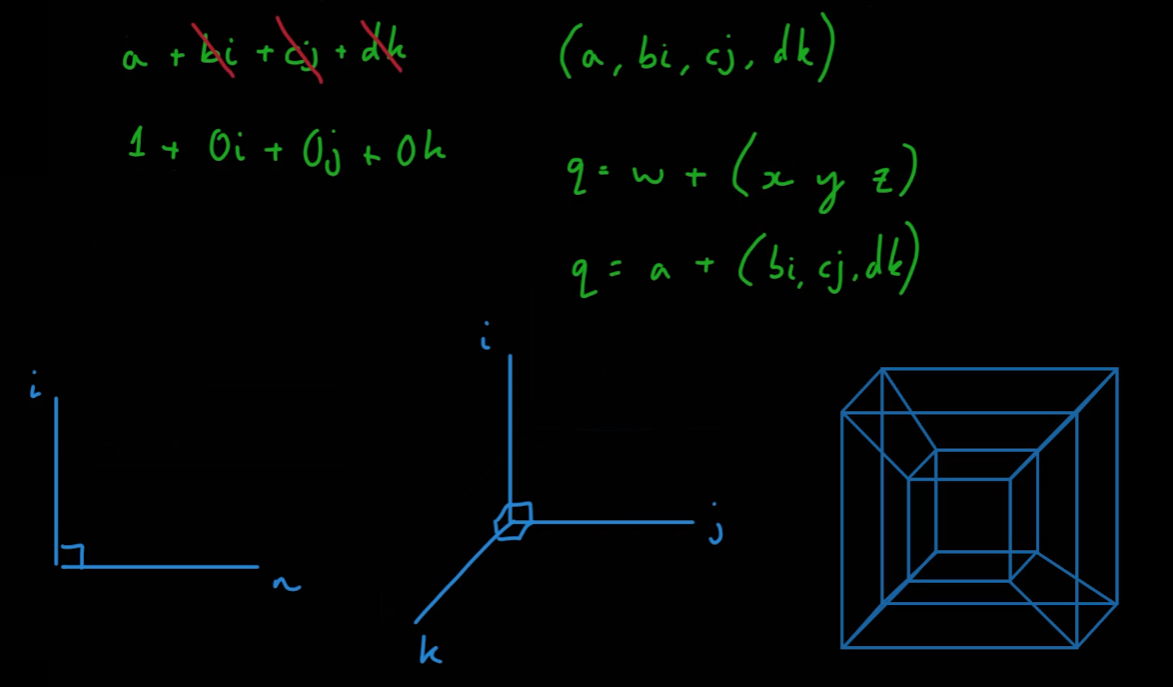
05_11_Quaternion Multiplication Part 1

• 일반적으로 쿼터니언을 나타내는 방법은 다음과 같다
  
• 쿼터니언에서 사용하는 허수 i, j, k는 다음과 같은 식이 성립한다.
  • i^2 = j^2 = k^2 = ijk = -1
  • ij = -ji
• 위의 식을 바탕으로 허수 i, j, k에 대한 곱셈 행렬이 다음과 같이 도출된다.
  
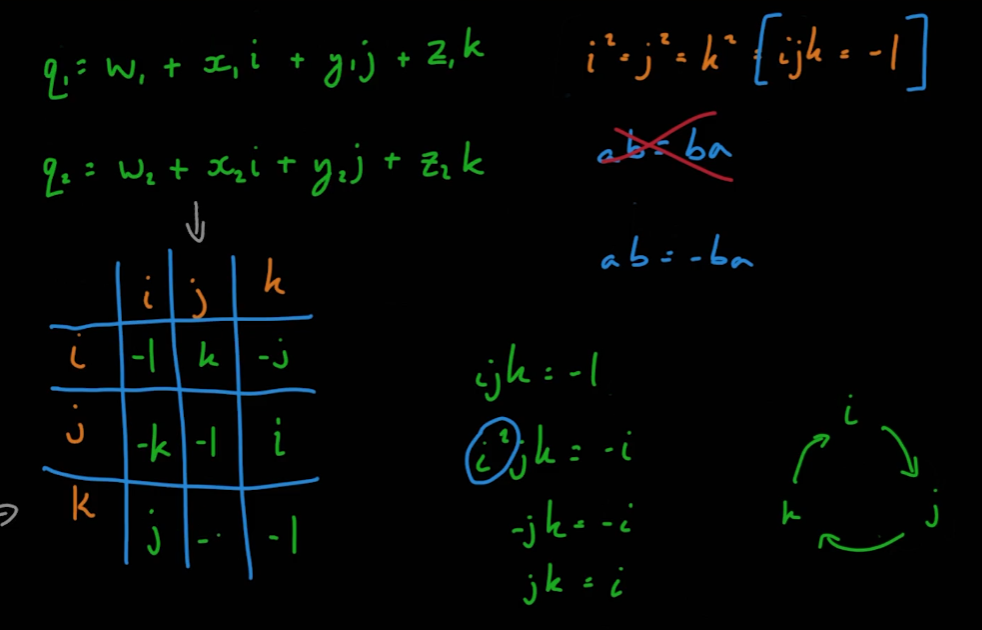
• 따라서 두 쿼터니언의 곱은 다음과 같이 도출된다.
  
  
  

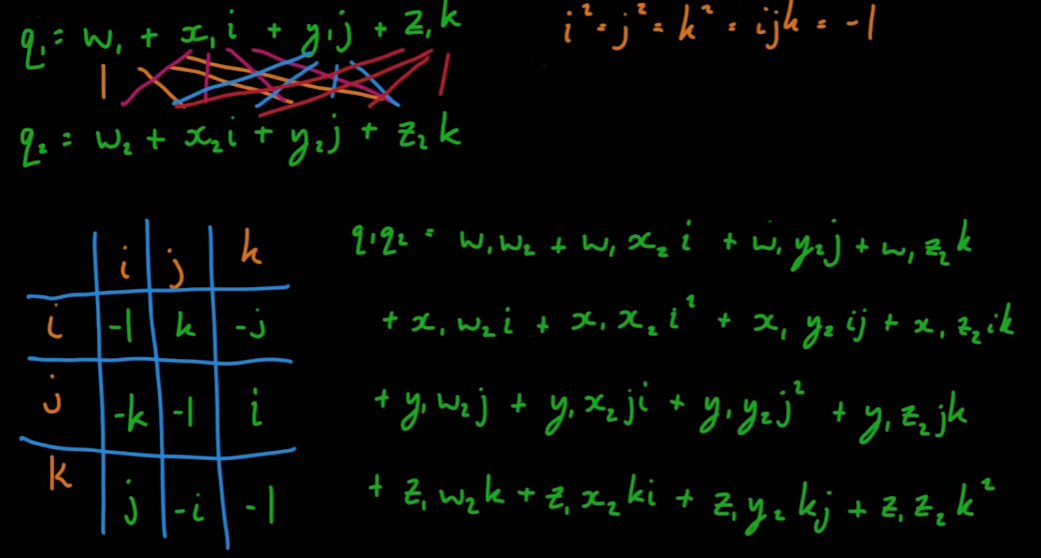
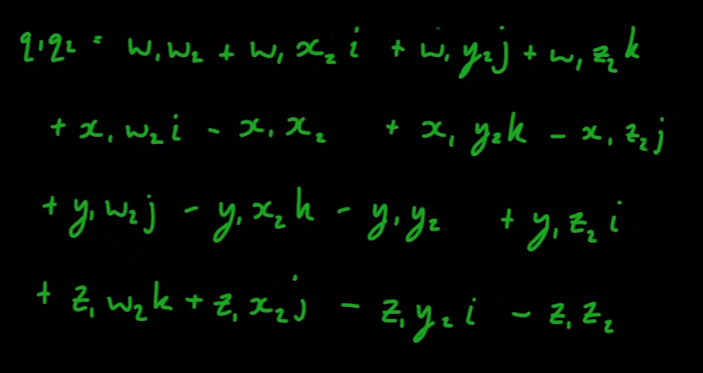
05_12_Quaternion Multiplication Part 2

• 이전 강의에서 도출된 식은 다음과 같다
  
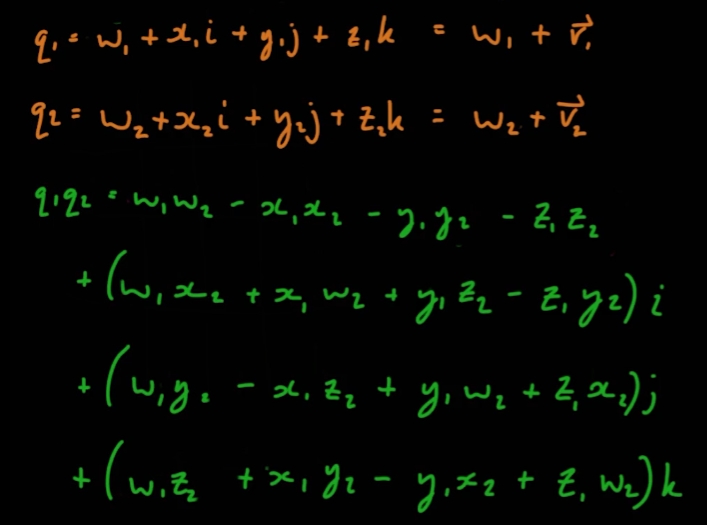
• 이 식을 내적과 외적을 사용해 다음과 같이 축약할 수 있다.
  • 쿼터니언의 실수부는 두 실수부의 곱에 두 허수부의 내적값을 뺀 것이다
  • 쿼터니언의 허수부는 세 가지 방법으로 나눌 수 있다.
    - 첫 번째 쿼터니언의 실수부에 두 번째 쿼터니언의 허수부 벡터를 곱한 값
    - 두 번째 쿼터니언의 실수부에 첫 번째 쿼터니언의 허수부 벡터를 곱한 값
    - 두 허수부 벡터의 외적값
    
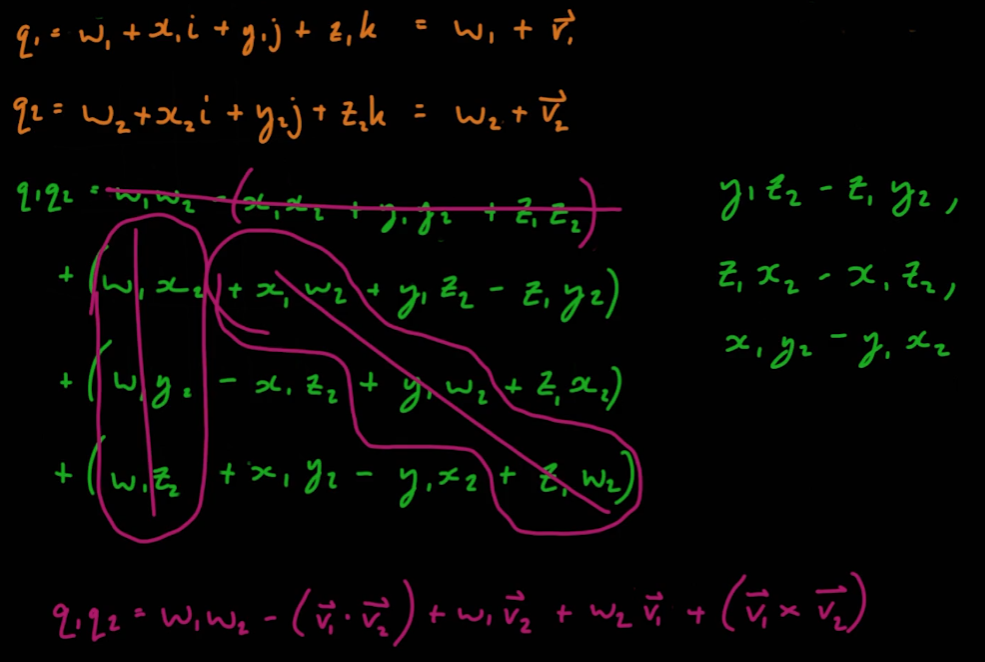
• 또한 위의 식을 이용해 4X4 쿼터니언 행렬을 만들 수 있다
  • 두 행렬의 결과값은 동일하다
    

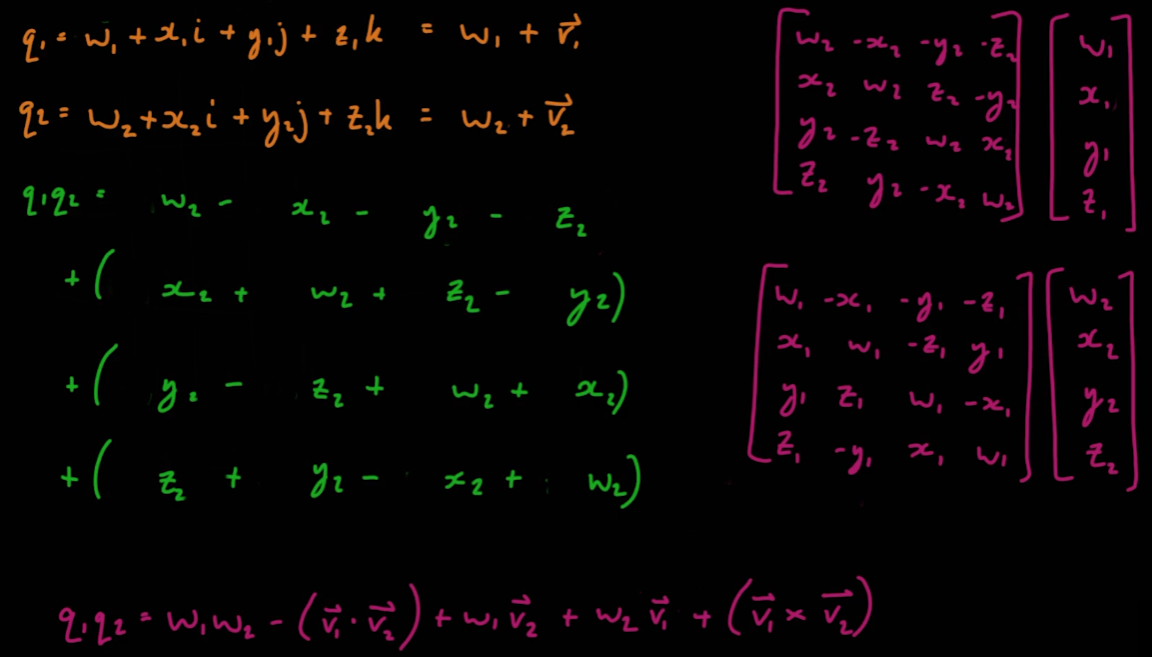
05_13_Quaternion Rotation Part 1

• 쿼터니언에서의 회전은 4차원을 기준으로 잡는다.
• 아래 그림은 실수 1을 원점으로 하는 3차원 허수좌표계이다. 이 때 허수 i를 기준으로 회전을 한다고 하면 다음과 같은 두 종류의 회전이 발생한다.
  
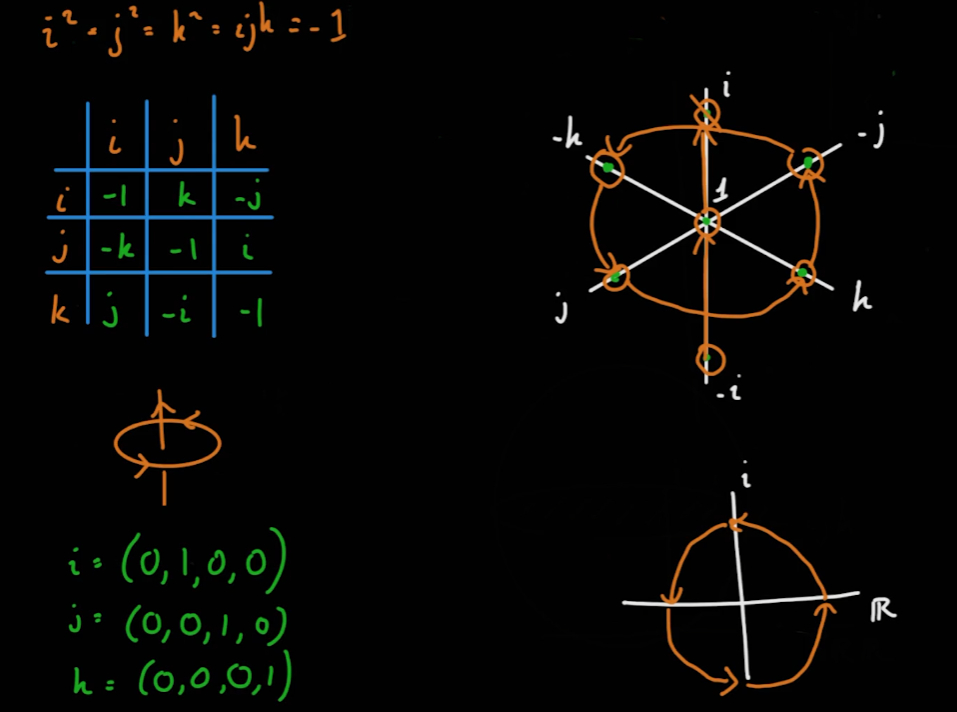
  • i축으로의 회전은 다음과 같다.
    • 다음의 오른쪽 아래 그림에서 실수 1이 90도 회전하여 i가 되면 오른쪽 위 그림의 실수 1에 대한 3차원 허수 좌표의 원점(0, 0, 0)에 있던 점이 (i, 0, 0)으로 이동한다.
    • i가 90도 회전하여 -1이 되면 실수부를 포함하여 존재하는 4차원 좌표계로 점이 넘어간다
    • -1이 90도 회전하여 -i가 되면 4차원 좌표계에 있던 점이 (-i, 0, 0)에 생겨난다
    • -i에서 90도 회전하여 1이 되면 다시 점이 (0, 0, 0)으로 돌아온다
  • j, k축의 회전은 서로간의 회전이 된다.
    • i * j = k, i * k = -j, i * -j = -k, -k * i = j
• 쿼터니언의 켤레는 허수부의 부호만 바꿔주면 된다
  

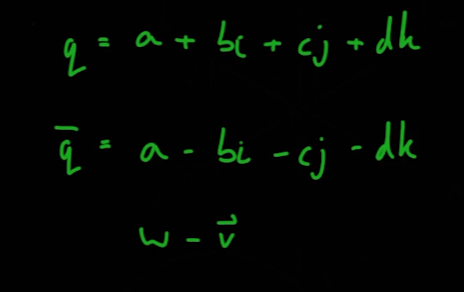
05_14_Quaternion Rotation Part 2

• 쿼터니언 회전은 0~360이 아닌 -180에서 180의 각을 가지게 된다
  

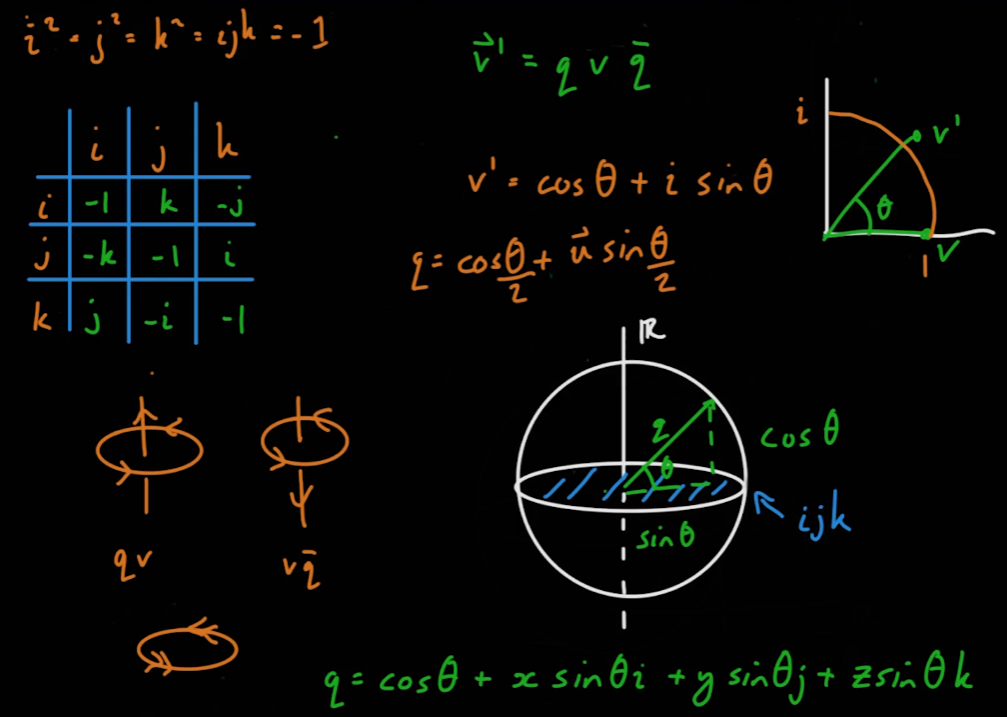
05_15_LERP

위키피디아 - 선형 보간

• 두 점 사이를 보간하는 방법은 여러 가지가 있지만, 이중 일직선으로 연결한 것을 선형 보간이라 한다.
  

05_16_SLERP

구면 선형 보간

• 두 점 사이를 호를 그리며 보간하는 방법을 구면 선형 보간법이라 한다.
  

05_07_Easing Functions

Easing Function

• 시간 흐름에 따른 매개변수의 변화율을 뜻한다
• 이를 이용해 자연스러운 값 변화를 나타낼 수 있다.
  
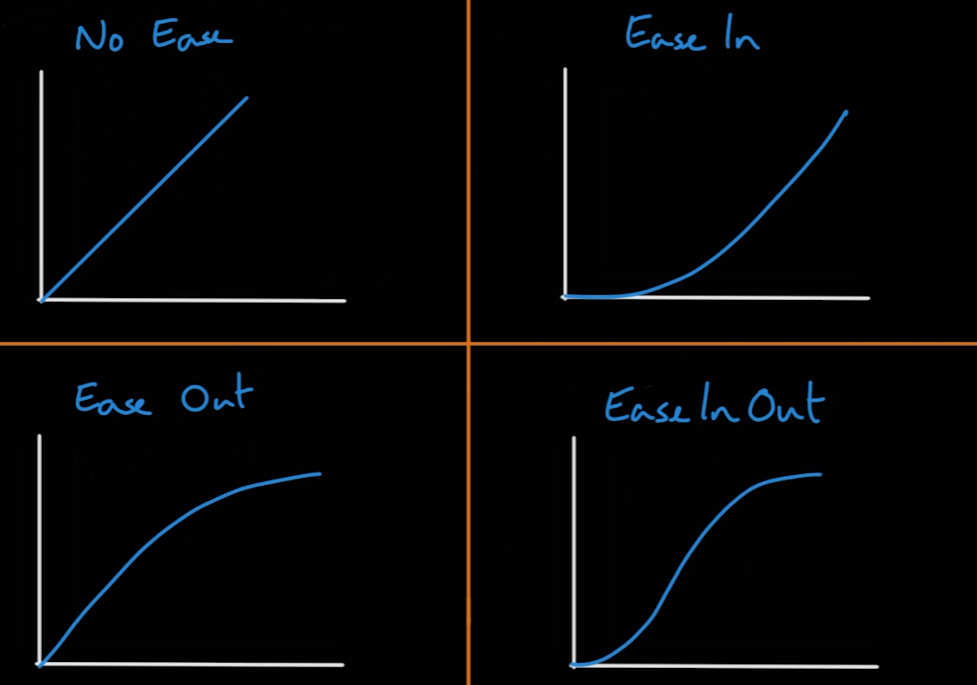
• 위 4개의 그래프에 대한 식은 다음과 같다.(단 0 <= t <= 1)
  • LERP : a + (b - a) * t
  • EaseIn : a + (b - a) * t^2
  • EaseOut : a - (b - a) * (t * (t - 2))
  • EaseInOut : a - (b - a) * cos(pi * t)