[프로그래머스] PCCP 기출문제 4번 (JavaScript)

문제 설명[링크]

n x m 크기 격자 모양의 퍼즐판이 주어집니다.

퍼즐판에는 빨간색 수레와 파란색 수레가 하나씩 존재합니다. 각 수레들은 자신의 시작 칸에서부터 자신의 도착 칸까지 이동해야 합니다.
모든 수레들을 각자의 도착 칸으로 이동시키면 퍼즐을 풀 수 있습니다.

당신은 각 턴마다 반드시 모든 수레를 상하좌우로 인접한 칸 중 한 칸으로 움직여야 합니다. 단, 수레를 움직일 때는 아래와 같은 규칙이 있습니다.

수레는 벽이나 격자 판 밖으로 움직일 수 없습니다.
수레는 자신이 방문했던 칸으로 움직일 수 없습니다.
자신의 도착 칸에 위치한 수레는 움직이지 않습니다. 계속 해당 칸에 고정해 놓아야 합니다.
동시에 두 수레를 같은 칸으로 움직일 수 없습니다.
수레끼리 자리를 바꾸며 움직일 수 없습니다.
예를 들어, 아래 그림처럼 n = 3, m = 2인 퍼즐판이 있습니다.

속이 빨간색인 원은 빨간색 수레를 나타냅니다.
속이 파란색인 원은 파란색 수레를 나타냅니다.
테두리가 빨간색인 원은 빨간색 수레의 도착 칸을 나타냅니다.
테두리가 파란색인 원은 파란색 수레의 도착 칸을 나타냅니다.
위 퍼즐판은 아래와 같은 순서로 3턴만에 풀 수 있습니다.

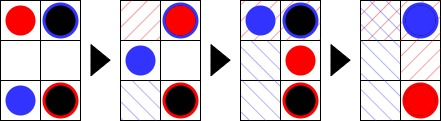
빨간색 사선이 처진 칸은 빨간색 수레가 방문했던 칸을 나타냅니다. 규칙에 따라 빨간색 수레는 빨간색 사선이 처진 칸(방문했던 칸)으로는 이동할 수 없습니다.
파란색 사선이 처진 칸은 파란색 수레가 방문했던 칸을 나타냅니다. 규칙에 따라 파란색 수레는 파란색 사선이 처진 칸(방문했던 칸)으로는 이동할 수 없습니다.

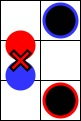
위처럼 동시에 수레를 같은 칸으로 움직일 수는 없습니다.
퍼즐판의 정보를 나타내는 2차원 정수 배열 maze가 매개변수로 주어집니다. 퍼즐을 푸는데 필요한 턴의 최솟값을 return 하도록 solution 함수를 완성해 주세요. 퍼즐을 풀 수 없는 경우 0을 return 해주세요.

풀이

function solution(maze) {
  const colLen = maze.length;
  const rowLen = maze[0].length;
  const pos = [null, null, null, null];
  const dest = [null, null, null, null];
  const redVisited = new Array(colLen)
    .fill()
    .map(_ => new Array(rowLen).fill(false));
  const blueVisited = new Array(colLen)
    .fill()
    .map(_ => new Array(rowLen).fill(false));
  const moves = [
    [1, 0],
    [-1, 0],
    [0, 1],
    [0, -1],
  ];

  for (let i = 0; i < colLen; i += 1) {
    for (let j = 0; j < rowLen; j += 1) {
      if (maze[i][j] === 1) {
        pos[0] = i;
        pos[1] = j;
        redVisited[i][j] = true;
      } else if (maze[i][j] === 2) {
        pos[2] = i;
        pos[3] = j;
        blueVisited[i][j] = true;
      } else if (maze[i][j] === 3) {
        dest[0] = i;
        dest[1] = j;
      } else if (maze[i][j] === 4) {
        dest[2] = i;
        dest[3] = j;
      }
    }
  }

  const posQueue = [pos];

  const getValidMoves = (x, y, isRed) => {
    const visited = isRed ? redVisited : blueVisited;
    const validMoves = [];

    for (const [dx, dy] of moves) {
      const [movedX, movedY] = [x + dx, y + dy];

      if (
        movedX >= 0 &&
        movedX < colLen &&
        movedY >= 0 &&
        movedY < rowLen &&
        maze[movedX][movedY] !== 5 &&
        !visited[movedX][movedY]
      ) {
        validMoves.push([movedX, movedY]);
      }
    }

    return validMoves;
  };

  const recursive = ([rx, ry, bx, by], count) => {
    if (rx === dest[0] && ry === dest[1] && bx === dest[2] && by === dest[3])
      return count;

    const redMoves =
      rx === dest[0] && ry === dest[1]
        ? [[rx, ry]]
        : getValidMoves(rx, ry, true);
    const blueMoves =
      bx === dest[2] && by === dest[3] ? [[bx, by]] : getValidMoves(bx, by);

    const min = [Infinity];

    for (const [rmx, rmy] of redMoves) {
      for (const [bmx, bmy] of blueMoves) {
        if (
          !(rmx === bx && rmy === by && bmx === rx && bmy === ry) &&
          !(rmx === bmx && rmy === bmy)
        ) {
          redVisited[rmx][rmy] = true;
          blueVisited[bmx][bmy] = true;
          min.push(recursive([rmx, rmy, bmx, bmy], count + 1));
          redVisited[rmx][rmy] = false;
          blueVisited[bmx][bmy] = false;
        }
      }
    }

    return Math.min(...min);
  };

  const result = recursive(pos, 0);

  return result === Infinity ? 0 : result;
}

결과