안녕하세요 양콩공입니다 !! 전 포스팅에서 언급했던 것처럼 [혁펜하임의 AI DEEP DIVE] 강의의 내용을 정리하는 포스팅을 시작해보려합니다!
오늘은 기초이자 중요한 함수, 벡터, 행렬에 대해 강의를 들은 내용과 새롭게 알게 되고 느낀 점에 대해 언급하겠습니다!
제가 필기한 강의자료와 함께 올리려고 합니다! 아직 아이패드에 익숙하지 않아서 악필이지만 이해해 주세요 ,,, 😢
본 게시글은 패스트 캠퍼스 [혁펜하임의 AI DEEP DIVE] 체험단 활동을 위해 작성되었습니다.
1. 함수
함수는 x라는 값이 입력되면, f라는 처리를 해서 f(x) 혹은 y를 뱉어내는 흐름입니다.
강사님은 박스 그림으로 함수를 표현하십니다!
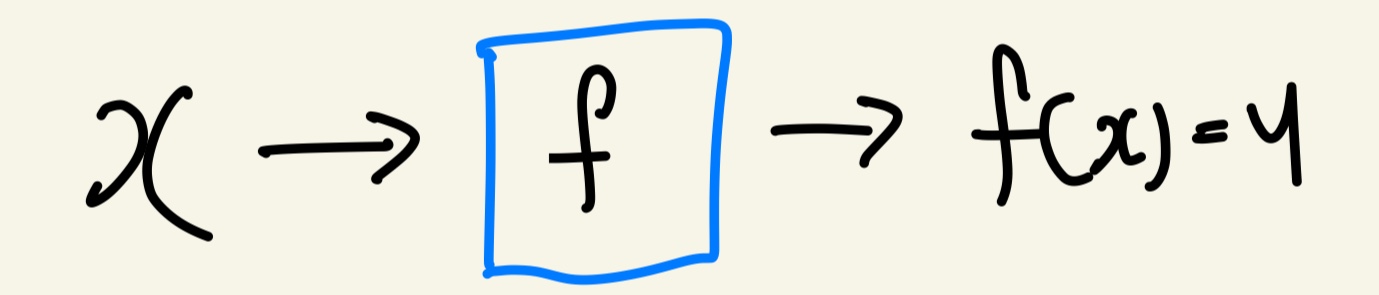
위처럼 한 개의 입력이 들어가고 한 개의 출력이 나오는 기본 2차 함수와 같은 형태도 있지만,
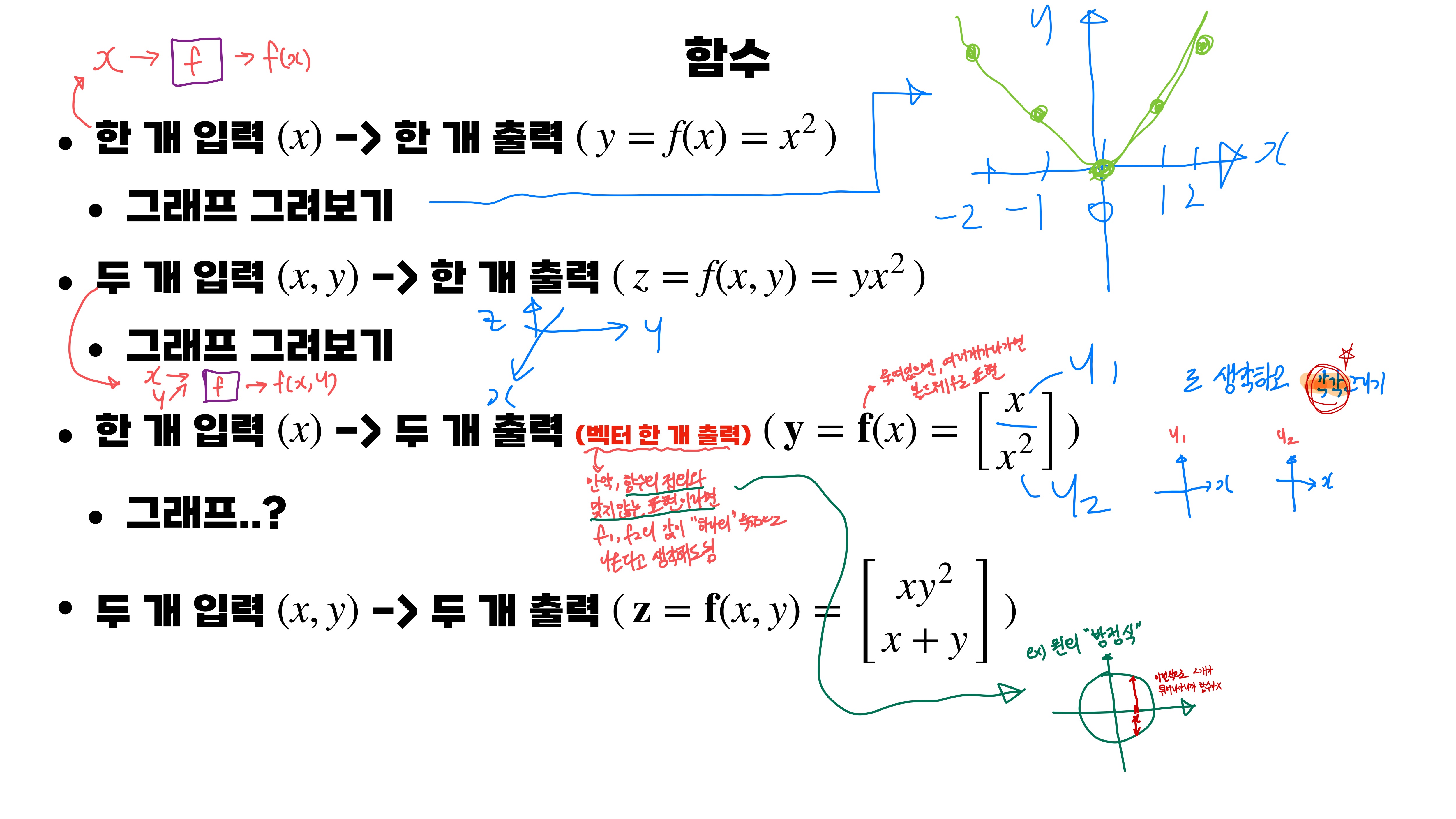
위의 자료처럼
-
두 개 입력하면, 한 개 출력이 나오고
-
한 개 입력하면, 두 개 출력이 나오고
-
두 개 입력하면, 두 개 출력이 나오는 경우가 있습니다.
2번 정의에서는 '함수의 정의에 맞지 않는 표현이다'라고 생각할 수 있습니다.
그렇다면, 자료에 나온 것처럼 한 개를 입력했을 때, 두 개가 하나의 묶음 즉, 벡터 한 개를 출력한다고 생각하면 함수로 정의할 수 있습니다.
그리고 자료에 제가 메모한 것을 보면, 2번에서 함수로 정의가 안 되는 경우는 원의 방정식과 같이 2개가 결과값으로 튀어나가는 경우를 예시로 들어주셨습니다! 이름처럼 함수가 아니라 '방정식'의 표현을 사용합니다!
3번 정의에서는 3차원으로 그래프를 그리면 가능합니다!
2. 로그 함수
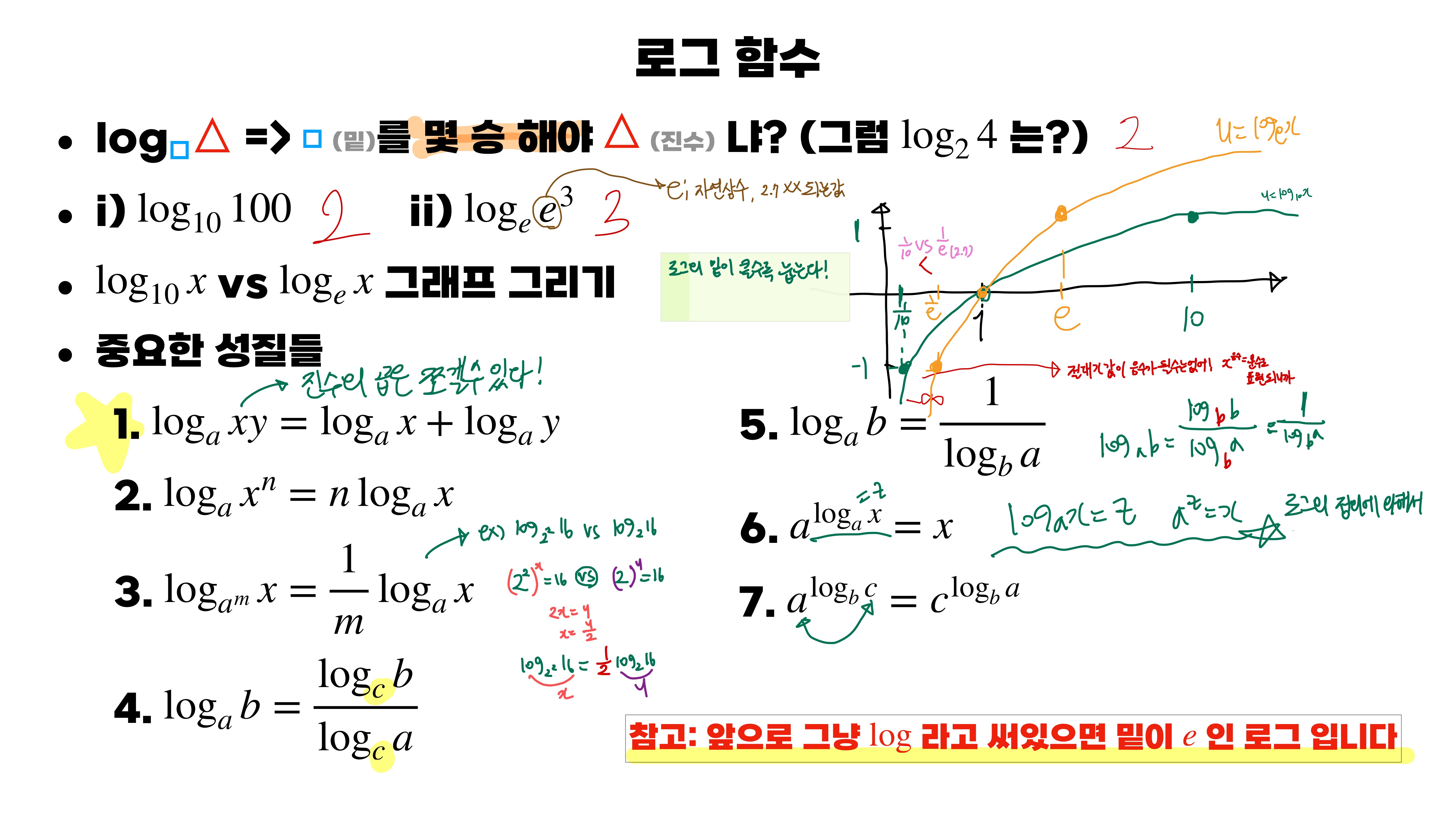
log 함수에 대해서 항상 헷갈리시는 분들이 많았을 거예요! 저도 항상를 생각할 때, 였지 하면서 두 번의 과정을 거쳐생각했습니다.
강사님이 그런 점을 아셨던 건지 자료에서 보시는 것과 같이 맨 위에처럼 기억하라고 길잡이를 해주셨어요!
그럼 바로 괄호 속 문제의 정답을 맞힐 수 있을 것입니다. 2를 몇 승해야 4가 나오나요? 2입니다.
와 의그래프를 그리면서 로그의 밑이 클수록 그래프가 눕는다는 것을 알았습니다.
그리고 log 함수의 그래프에 대해 외워서 공부하셨던 분들은 절대 입력 x 값이 음수가 될 수 없다는 것을 알면 쉬울 것 같아요!
x의 음수를 제곱하면 분수가 결과로 나오기 때문입니다.
마지막으로 중요한 성질들에 대해 짚어주셨고, 6번은 로그의 정의로 증명할 수 있으니 다들 한 번씩 해보셨으면 좋겠어요!
3. 벡터와 행렬
벡터와 행렬의 정의를 말씀하실 수 있을까요?
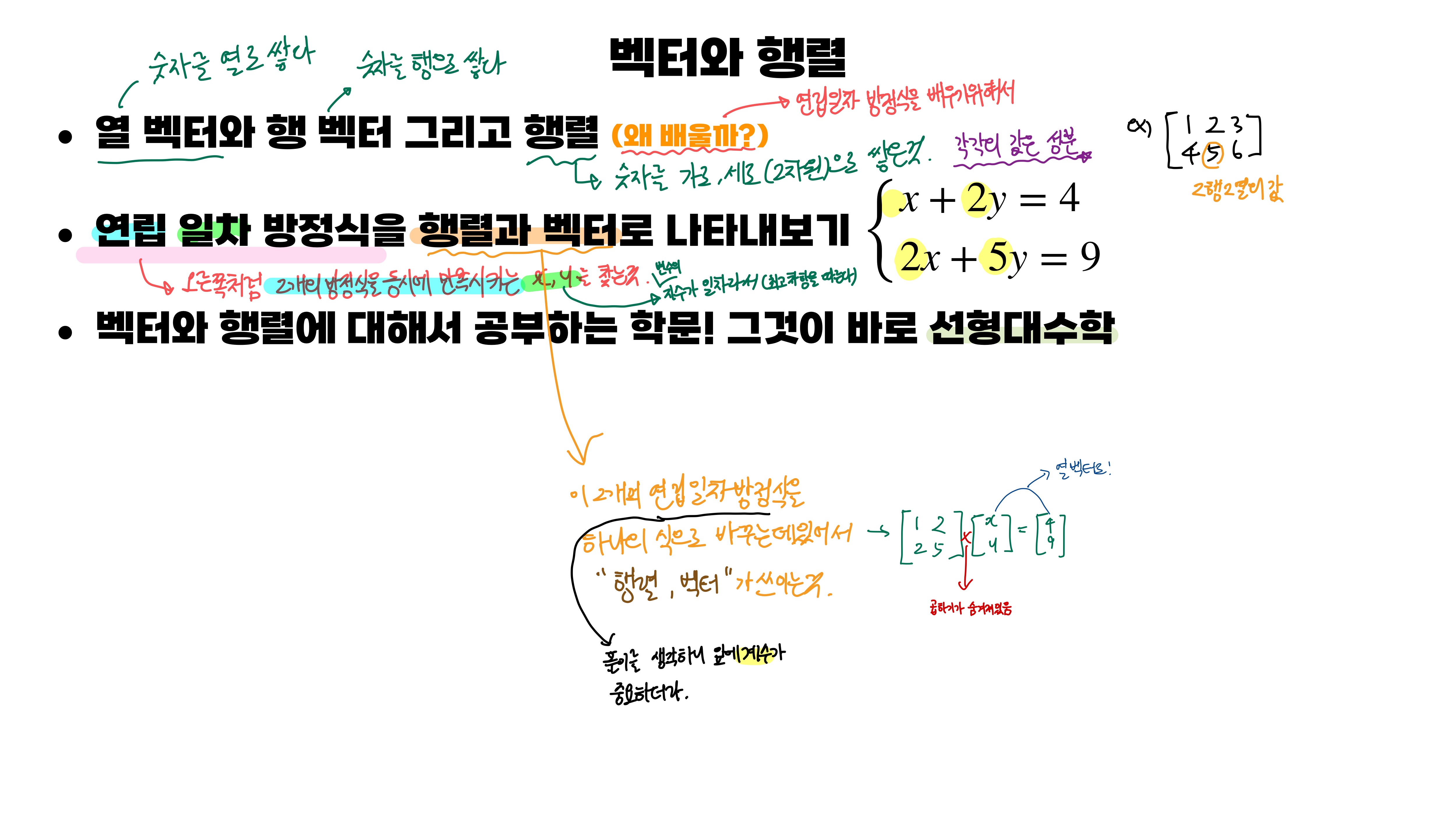
열벡터면 숫자를 열로 쌓은 것이고, 행 벡터는 숫자를 행으로 쌓은 것입니다.
그리고 행렬은 숫자를 2차원으로 쌓은 것입니다!
저는 행렬은 말할 수 있어도 벡터는 감이 안 잡혔는데 강사님 정의를 듣고 너무 쉬웠습니다 ..
왜 배울까요?
연립 일차 방정식을 배우기 위함입니다.
연립 일차 방정식은 자료 두 번째 줄 오른쪽의 식처럼 2개의 방정식을 동시에 만족시키는 x, y를 찾는 것입니다!
이 2개의 연립 일차 방정식을 '하나의' 식으로 바꾸는 데 있어서 행렬과 벡터가 쓰이는 것입니다!

행렬과 벡터의 곱으로 두 개의 연립 일차 방정식을 하나의 식으로 표현할 수 있다고 했습니다!
자료의 오른쪽 맨 위와 같이 '드르륵 드르륵' 해서 곱하면 가능한데요! 영상으로 설명드리면 쉬울 텐데,,, 강의를 보시면 쉬울 것 같습니다.
저의 필기가 이해가 되셨다면 2x2 행렬과 2x3 행렬을 곱할 수 있을지에 대한 의문을 해결할 수 있습니다!
2x2 계수 행렬에서 쓰는 계수와 같은 또 다른 열 벡터 변수가 있다면 곱할 수 있습니다!
여기서 주요 성질을 알 수 있죠! 2개의 행렬을 기준으로 앞에 '열'의 숫자와 뒤의 '행'의 숫자가 같으면 곱할 수 있습니다.
그리고 결과 사이즈는 필기와 같이 맨 앞 x 맨 뒤의 크기로 나오게 됩니다.
하지만 정말 중요한 점은 교환법칙이 성립하지 않습니다! 전혀 다른 식이 나와서 원래의 식으로 돌아갈 수 없기 때문입니다!

마지막으로 벡터의 방향과 크기에 대해 알아보겠습니다!
원점을 시점, [2,1] 좌표를 종점으로 놓으면 벡터를 화살표로 나타낼 수 있고, 방향을 가진다는 것을 알 수 있습니다.
크기와 방향이 같으면 같은 벡터라서 시점이 달라도 같은 벡터일 수 있습니다.
그리고 피타고라스의 정리에 따라 화살표의 길이로 벡터의 크기를 나타냅니다.
크기를 나타내는 것들에는 l2-norm과 l1-norm이 있다고 합니다!
함수, 벡터, 행렬 정말 기초적인 내용이지만 설명하라고 하면 어려웠던 분들이 많으셨을 거라고 생각합니다! 함수, 행렬은 그래도 알고 있었지만 벡터의 개념과 이 3개의 개념의 쓰임에 대해 알 수 있는 강의 내용이라 정말 좋았습니다! 너무 기초인데 왜 알아야 하는 거지라고 생각하실 수도 있지만 나중에 심화 개념에 가면 툭 하고 바로 튀어나와야 하는 개념이니까 중요하게 생각하셨으면 좋겠습니다!

