안녕하세요 양콩공입니다! 오늘은 나중에 정말 중요한 전치와 내적, 극한, 미분, 도함수에 대한 강의 내용을 정리하겠습니다!
[혁펜하임의 AI DEEP DIVE] 체험단 활동을 위해 작성되었습니다.
1. 전치와 내적
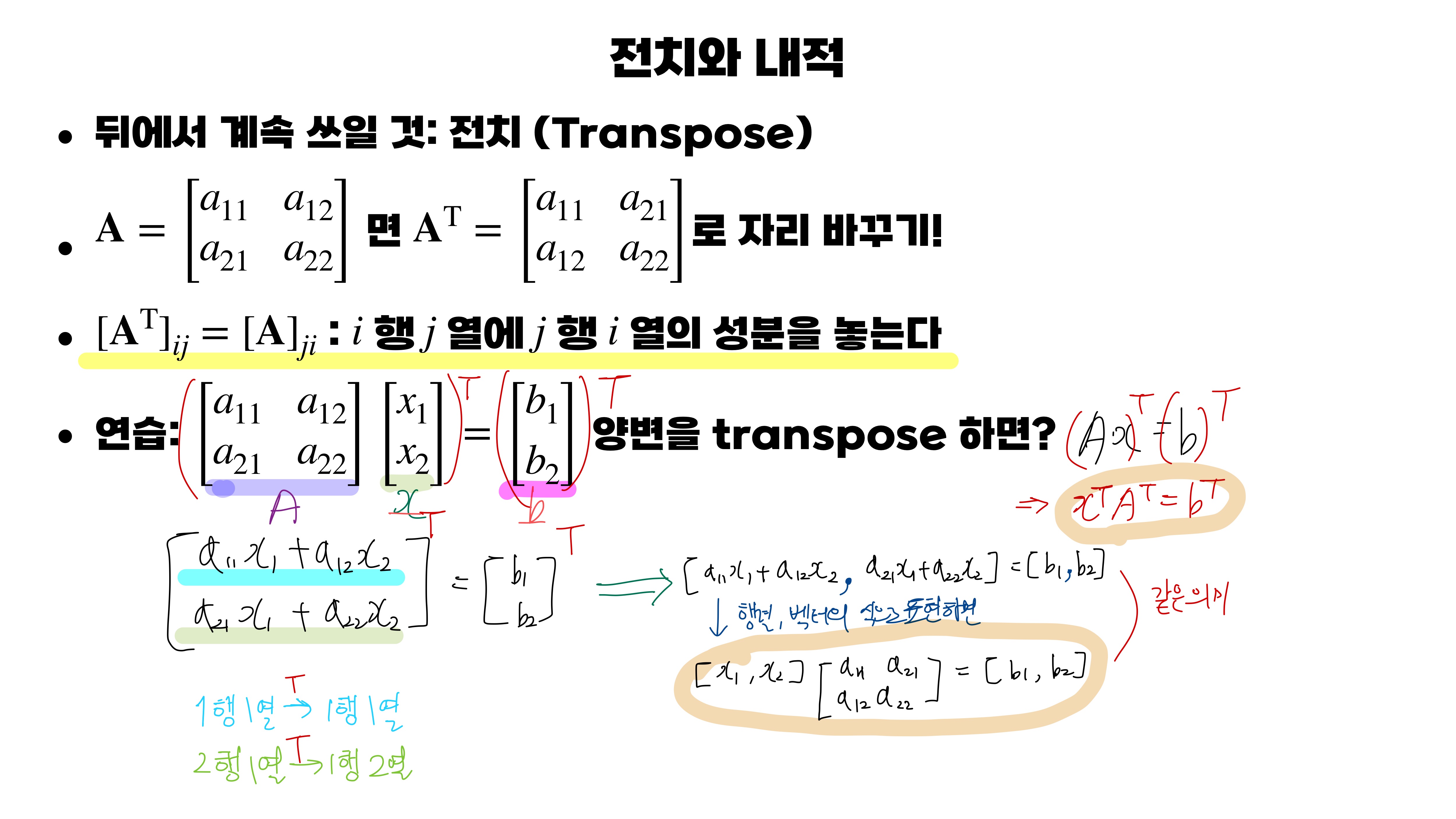
먼저, 전치입니다! 전치는 정말 두고두고 곱하기처럼 자주 나오는 연산입니다! 전치는 처음 봤을 때 저도 블로그 막 찾아보고 너무 어려웠는데.. 강의자료에 제가 노란 형광펜 칠한 부분 보시면 종결될 것입니다.
대각선 기준으로 바뀌는 게 아니라 사실 a11도 a22도
1행 1열에 1행 1열의 성분을 놓는다의 전치 정의를 따라간 것입니다!
이를 대각선 기준이라고 해도 되지만 저 정의 그대로 알고 계심을 더 추천합니다!
저 연습문제까지 푸신다면 전치를 완벽하게 이해한 것입니다!

내적은 벡터와 벡터의 dot product로, 결괏값으로 스칼라가 튀어나오게 됩니다.
또한 후에 CNN과 RNN에서 중요한 개념인 내적은 닮은 정도를 나타냅니다.
식을 보시면 두 벡터의 크기와 cos θ의 곱으로 표현할 수 있고, 닮은 정도의 증명은 제2 cos 법칙으로 증명할 수 있습니다! 자료를 보시면 가장 닮았을 때는 a 벡터와 b 벡터의 사잇각이 0도일 때임을 알 수 있습니다.
2. 극한
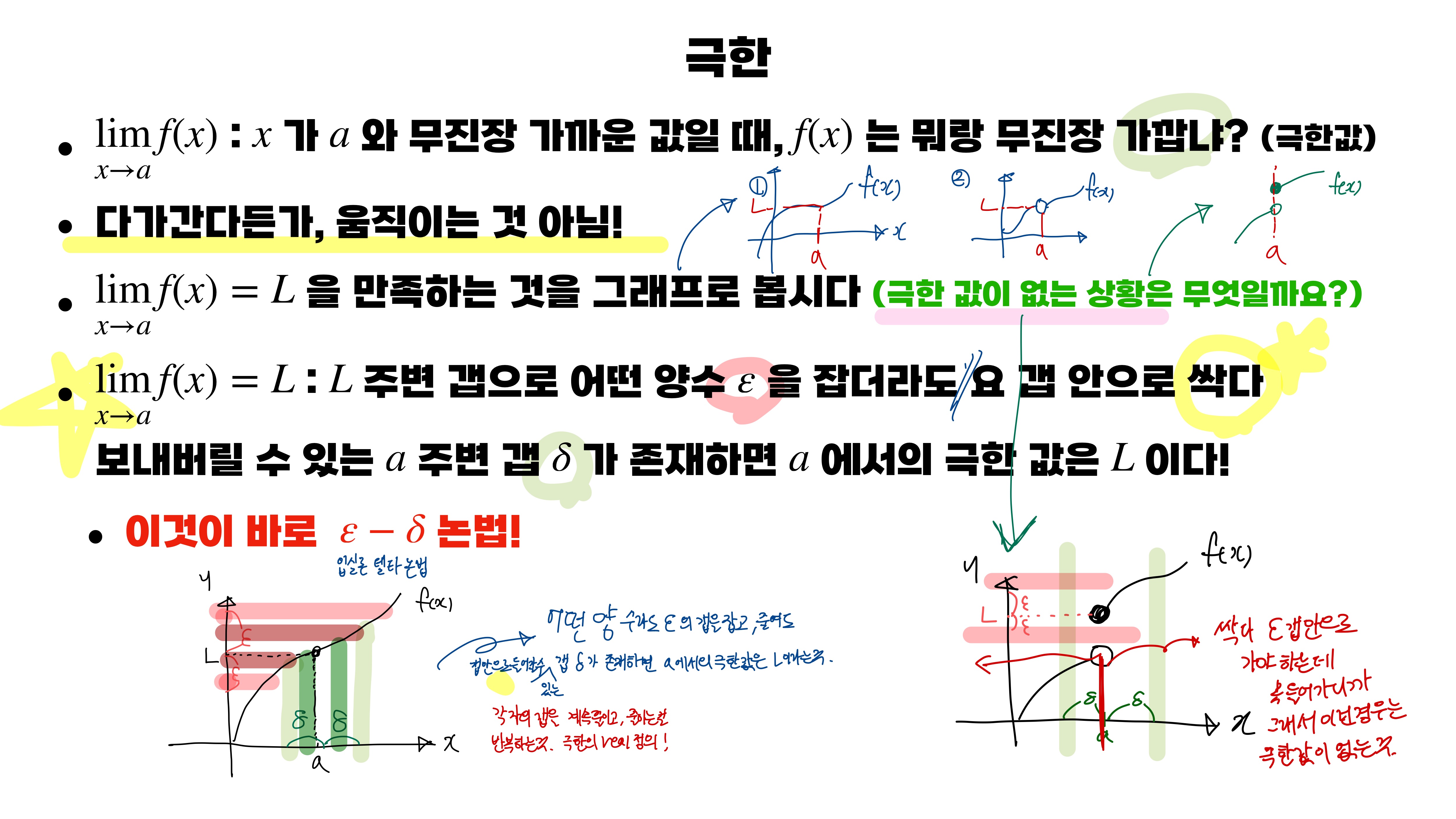
극한에 대해서 값으로 다가간다든가, 움직이는 개념으로 생각하면 안 된다는 것을 알았습니다.
Loss 주변 갭으로 어떤 양수 엡실론을 잡더라도, 해당 갭 안으로 싹 다 보내버릴 수 있는 특정 값(a) 주변 갭 델타가 존재하면! 특정 값(a)에서의 극한 값은 loss입니다
이것이 바로 극한을 엡실론-델타 논법으로 정의한 것입니다!
저도 원래 극한에 대해 특정 값에 가까워진다고 생각했었는데, 강사님의 설명으로 개념을 재정립할 수 있었습니다!
3. 미분

미분은 순간 변화율이라고 정의합니다. linear 말고는 기울기가 계속 변하기에 “순간 기울기”의 개념이 필요합니다!
예를 들어, x=1에서의 순간 기울기에 대해 알고 싶으면
1에서 그 순간을 의미하는 Δ x를 더한 값에 대한 y 값에서 1에서의 함수 값을 빼고, Δ x로 나눠 극한을 취하는 것입니다. 순간을 표현하기 위해서는 극한의 개념이 필요하기 때문입니다!
Δ x , 극한이 나와서 다른 개념 같다고 생각할 수 있지만 강의 자료의 예시와 같은 흐름이니 그렇게 이해해 주세요!
4. 도함수

위의 수식처럼 복잡하게 전개하지 말고, f(x)를 미분한 것을 함수로 두고, 순간 기울기를 알고 싶은 x 값을 넣어주자는 개념이 도함수입니다. 미분의 의미가 합쳐져서 도함수라고 부르는 것입니다.

위는 딥러닝 공부하면서 자주 보이는 도함수들이라 바로 튀어나올 수 있도록 학습하시면 좋을 거 같습니다!
아직 너무 쉬운 개념이라 간단 간단하게 넘어가서 중요하지 않다고 생각할 수 있지만 혁펜하임님의 강의 구성은 앞에서 배운 내용이 점점 level1,2,3로 응용이 되기에 덜 중요한 개념이 하나도 없으니 꼭 쉽더라도 의문을 던지면서 학습하시면 도움이 되실 거라 생각됩니다!! ☺️

