오늘의 학습
- 모집단과 표본
- 표본오차와 신뢰구간
- 모집단과 분포
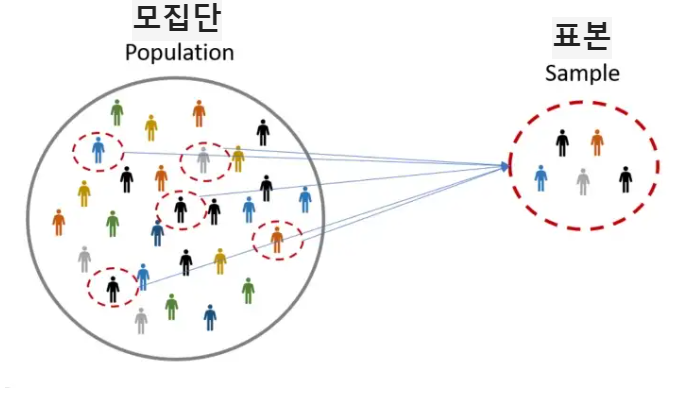[사진 출처 : https://brunch.co.kr/@saetae/101]
[표본을 사용하는 이유]
1️⃣ 비용과 시간이 절약 + 유의미한 결과 도출 가능
2️⃣ 무작위로 표본 추출해 모집단 전체 일반화 가능
3️⃣ 데이터 처리 및 관리 용이
[실제 사용하는 경우]
1️⃣ 도시 연구
2️⃣ 의료 연구
3️⃣ 시장 조사
4️⃣ 정치 여론 조사
[파이썬 실습]
import numpy as np
import matplotlib.pyplot as plt
# 모집단 생성
population = np.random.normal(170, 10, 1000)
# 표본 추출
sample = np.random.choice(population, 100)📍 numpy.random 모듈
➖ Numpy 라이브러리 일부
➖ 다양한 확률 분포에 따라 난수 생성
📍 np.random.normal
➖ 정규분포를 따르는 난수 생성
➖ loc(float) : 정규분포 평균 (기본값 0.0)
➖ scale(float) : 정규분포 표준편차 (기본값 1.0)
➖ size(int/tuple of ints) : 데이터 개수(크기) (기본값 None-스칼라 값 반환)
📍 np.random.choice
➖ 주어진 배열에서 임의로 샘플링하여 요소 선택
➖ 무작위로 선택된 요소 반환
➖ a(1-D arrary-like or int) : 샘플링할 원본 배열 (정수인 경우 np.arange(a)와 동일하게 간주)
➖ size(int/tuple of ints) : 데이터 개수(크기) (기본값 None-단일값 반환)
➖ replace(boolean) : 복원 추출 여부 (기본값 True-동일한 요소 여러 번 선택 가능성 O)
➖ p(1-D array-like, optional) : 각 요소가 선택될 확률 (배열의 합은 1)
- 표본오차와 신뢰구간
[표본오차(Sampling Error)]
➖ 표본에서 계산된 통계량과 모집단의 진짜 값 간의 차이
➖ 표본 크기 클수록, 즉 데이터가 많을수록 표본오차 작아짐
[신뢰구간(Confidence Interval)]
➖ 모집단의 특정 파라미터에 대해 추정된 값이 포함될 것으로 기대되는 범위
➖ 신뢰구간 = 표본평균 +- z * 표준오차
- z : 선택된 신뢰수준에 해당하는 z-값
➖ 일반적으로 95% 신뢰수준 사용
[파이썬 실습]
# 통계 계산 시 사용하는 라이브러리 stats
import scipy.stats as stats
# 표본 평균
sample_mean = np.mean(sample)
# 표본 표준편차
sample_std = np.std(sample)
# 95% 신뢰구간 계산
conf_interval = stats.t.interval(0.95, lem(sample)-1, loc=sample_mean, scale=sample_std/np.sqrt(len(sample)))📍 scipy.stats
➖ SciPy 라이브러리 일부
➖ 통계 분석을 위한 다양한 함수와 클래스 제공 모듈
📍 scipy.stats.t.interval
➖ 신뢰 수준에서 t-분포를 사용하여 신뢰 구간 계산
➖ alpha : 신뢰수준
➖ df : 자유도 (표본-1(n-1))
➖ loc : 표본 평균(위치)
➖ scale : 표본 표준 오차(표본 표준편차를 표본 크기의 제곱근으로 나눈 값 (sample_std/sqrt(n)))
