[내일배움캠프] 통계학 기초 (3)

오늘의 학습
1. 정규분포
2. 긴 꼬리 분포
3. 스튜던트 t 분포

---

1. 정규분포

[출처: 위키백과]

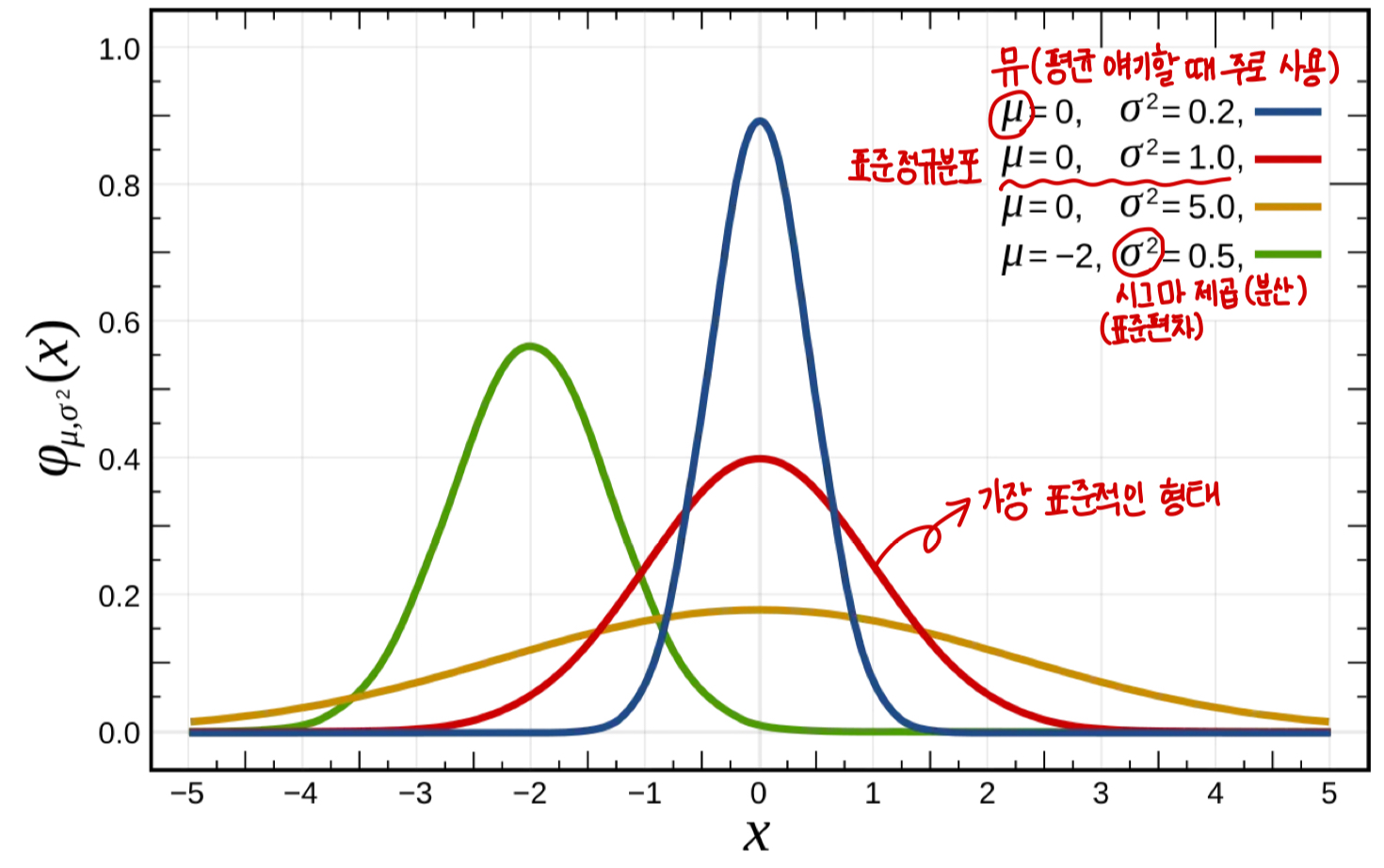
[정규분포란?]

➖ 종 모양 & 평균 중심으로 좌우 대칭 분포
➖ 데이터가 평균 주위에 몰려 있는 분포

[특징]

➖ 대부분의 데이터가 평균 주변에 몰려있음
➖ 평균에서 멀어질수록 데이터 빈도 감소 ⬇️
➖ 평균과 분산에 따라 다른 형태
➖ 표준편차는 분포의 퍼짐 정도 표시 (표준편차가 클수록 넓어지는 형태)
➖ 곡선은 확률값 표현, 모두 더하면 1
⭐️ 표본 선정 시 값이 충분히 크다면 웬만하면 거의 정규분포를 따라감!
= 중심극한정리

[파이썬 실습]

# 정규분포 생성 - 신장
normal_dist = np.random.normal(170, 10, 1000) 

📍 np.random.normal(170, 10, 1000) 
➖ 평균:170, 표준편차: 10 인 데이터 1000개 뽑는다는 의미


# 히스토그램으로 시각화
plt.hist(normal_dist, bins=30, density=True, alpha=0.6, color='g') 

📍 normal_dist, bins=30, density=True, alpha=0.6
➖ bins는 구간을 30개로 나눈다는 의미
➖ density는 확률 밀도 바꿔서 그래프 총 면적 1이 되도록 함
➖ alpha는 투명도로 1에 가까울수록 진함

# scipy 라이브러리 사용
import scipy.stats as stats

📍 scipy
➖ 수학 관련된 계산을 도와주는 라이브러리

📍 stats
➖ 통계 관련 기능이 들어 있는 부분으로 정규분포 곡선 그려줌

# 정규분포 곡선 추가
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = stats.norm.pdf(x, 170, 10)
plt.plot(x, p, 'k', linewidth=2)
plt.title('normal distribution histogram')
plt.show()

📍 xmin, xmax = plt.xlim()
➖ x축의 최댓값, 최솟값 가져와서 x축 범위 파악

📍 np.linspace(xmin, xmax, 100)
➖ xmin ~ xmax 범위의 100개의 점을 일정하게 나눠서 만듦 (곡선)

📍 stats.norm.pdf(x, 170, 10)
➖ 평균 170, 표준편차 10의 확률밀도함수(p.d.f) 값 계산

📍 plt.plot(x, p, 'k', linewidth=2)
➖ x랑 p를 이용해서 선 그림
➖ 'k'는 검정색(black) 선 의미
➖ linewidth=2는 선 두께

---

2. 긴 꼬리 분포

[긴 꼬리 분포]

➖ 대부분 데이터가 분포 한쪽 끝에 몰려 있으며 반대쪽으로 긴 꼬리가 이어지는 형태
➖ 비대칭적
➖ 여러 종류의 분포 O : 파레토 분포(기본), 지프의 법칙, 멱함수

[특징]

➖ 소득분포, 온라인 쇼핑, 도서 판매 등에서 사용
➖ 소수의 데이터가 큰 영향을 끼침
⭐️ 다른 분포와 달리 아무리 데이터가 많아져도 정규분포 XXX

[파이썬 실습]

# 긴 꼬리 분포 생성 - 소득 데이터
long_tail = np.random.exponential(1, 1000)

📍 np.random.exponential(1, 1000)
➖ np.random : 무작위로 숫자 데이터를 만들어주는 NumPy의 도구
➖ .exponential() : 지수분포(exponential distribution)에서 숫자 뽑는다는 의미
➖ (1, 1000) : scale 값(평균이 1인 지수분포) 1000개 만든다는 의미

# 히스토그램으로 시각화
plt.hist(long_tail, bins=30, density=True, alpha=0.6, color='b')
plt_title('long tail distribution histogram')
plt.show()

---

3. 스튜던트 t 분포

[출처: 위키백과]

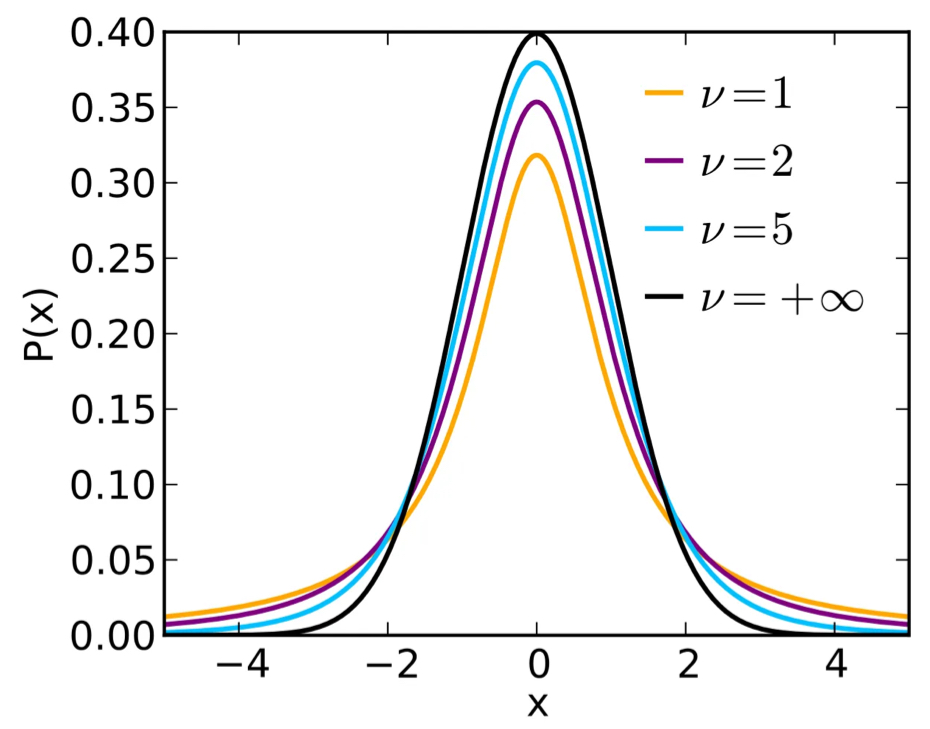
[스튜던트 t 분포]

➖ t분포는 모집단의 표준편차 모르고 표본 크기 작은 경우 정규분포 대신 사용 (30 미만)

[특징]

➖ 정규분포와 유사하나 표본 크기가 작을수록 꼬리가 두꺼워짐
➖ 자유도 커질수록 정규분포에 가까워짐 (자유도: 표본 크기와 관련 있는 값)
➖ 작은 표본 평균 비교나 약물 시험 등에 사용

[파이썬 실습]

# 스튜던트 t 분포 생성
t_dist = np.random.standard_t(df=10, size=1000)

📍 standard_t
➖ t-분포에서 숫자를 무작위로 뽑는 함수

📍 df=10
➖ degrees of freedom = 자유도
➖ 자유도가 10인 t-분포

📍 size=1000
➖ 데이터 1000개 무작위로 뽑으라는 의미

# 히스토그램으로 시각화
plt.hist(t_dist, bins=30, density=True, alpha=0.6, color='r')

# 스튜던트 t 분포 곡선 추가
x = np.linspace(-4, 4, 100)
p = stats.t.pdf(x, df=10)
plt.plot(x, p, 'k', linewidth=2)
plt.title('student t distribution histogram')
plt.show()