오늘의 학습
- 카이제곱분포
- 이항분포
- 푸아송 분포
- 카이제곱분포
 [출처: 위키백과]
[출처: 위키백과]
*그래프에서 K값 : 자유도 = 표본의 크기와 관련이 있는 값이다 정도로 이해!
[카이제곱분포란?]
➖ 범주형 데이터 분석할 경우 사용
➖ 분포독립성 검정 or 적합도 검정에 사용되는 분포
[공통 특징]
➖ 자유도에 따라 모양 상이
➖ 상관관계나 인과관계를 판별하고자 하는 원인의 독립변수가 ‘완벽하게 서로 다른 질적 자료’일 때 활용
➖ 성별이나 나이에 따른 선거 후보 지지율 구할 때 사용
[독립성 검정]
➖ 두 범주형 변수 간의 관계가 있는지 확인할 때 사용
➖ 성별과 직업 선택 간의 독립성을 검토 가능
➖ 성별이 후보 지지율에 영향을 끼치는지 검토 가능
[적합도 검정]
➖ 관측한 값들이 특정 분포에 해당하는지 검정할 때 사용
➖ 주사위의 각 면이 동일한 확률로 나오는지 검토 가능
➖ 노란색 완두와 녹색완두가 3:1의 비율로 나와야 하는데 실험적으로 측정한 데이터가 그렇게 나오는지 검토 가능
[파이썬 실습]
# 카이제곱분포 생성
chi2_dist = np.random.chisquare(df=2, size=1000)
📍 np.random.chisquare(df=2, size=1000)
➖ chisquare: 카이제곱(χ²) 분포를 따르는 난수 생성
➖ df: 자유도
➖ size: 1000개 데이터
# 히스토그램으로 시각화
plt.hist(chi2_dist, bins=30, density=True, alpha=0.6, color='m')
# 카이제곱분포 곡선 추가
x = np.linspace(0, 10, 100)
p = stats.chi2.pdf(x, df=2)
plt.plot(x, p, 'k', linewidth=2)
plt.title('카이제곱 분포 히스토그램')
plt.show()- 이항분포
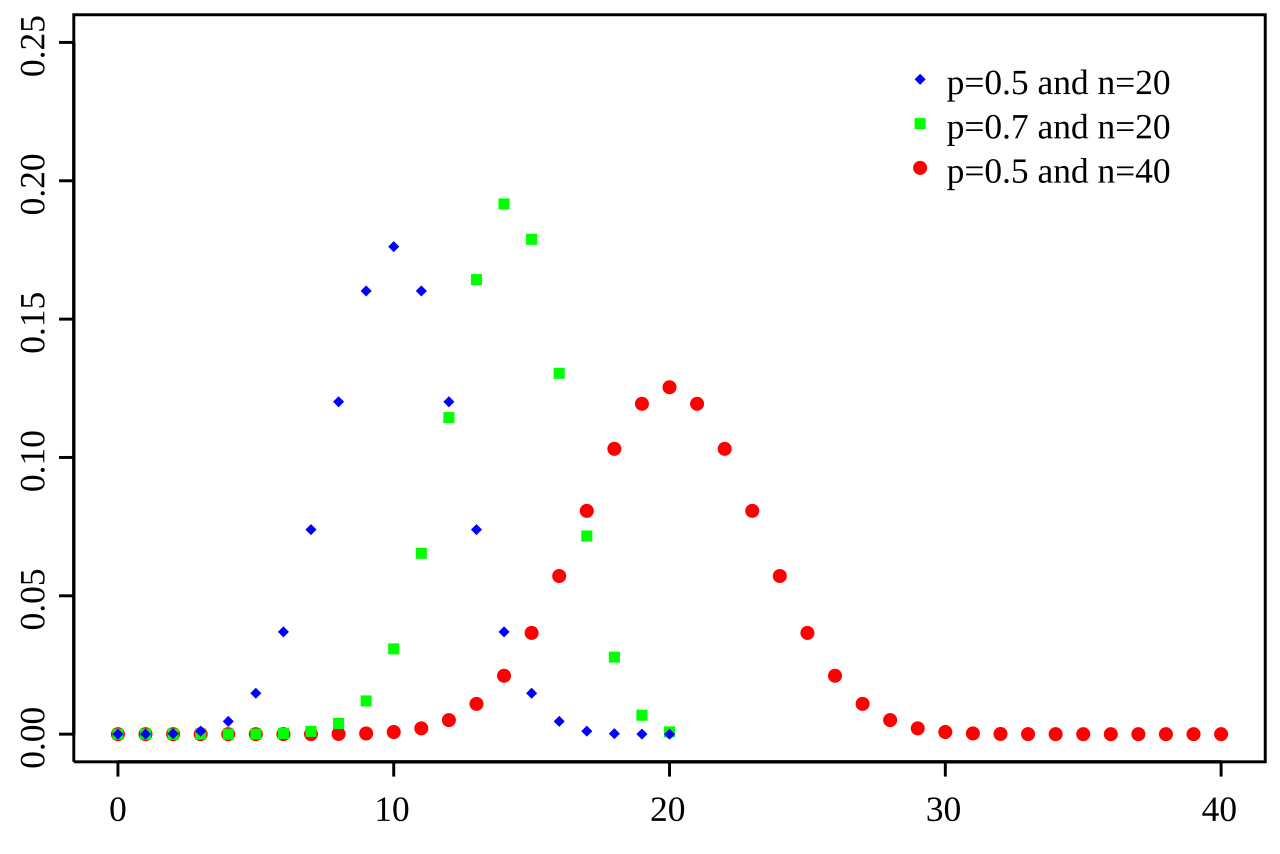
[이항분포란?]
➖ 성공/실패와 같은 결과가 2개가 나오는 실험을 여러 번 반복했을 때 성공 횟수의 분포
➖ 독립적인 시행이 n번 반복되고, 각 시행에서 성공과 실패 중 하나의 결과만 가능한 경우를 모델링하는 분포
➖ 성공 확률을 p라 했을 경우, 성공의 횟수를 확률적으로 나타냄
➖ 실험 횟수(n)와 성공 확률(p)로 정의
[특징]
➖ 이항분포는 연속된 값 X, 특정한 정수 값만 가짐
➖ 동전을 10번 던질 때 앞면이 나오는 횟수는 0, 1, 2, ..., 10과 같은 정수
➖ 이항분포 연속적으로 그려지지 X
➖ 연속된 값을 가지지 않기 때문에 이산형 분포라고도 부름
[파이썬 실습]
# 이항분포 생성 (예: 동전 던지기 10번 중 앞면이 나오는 횟수)
binom_dist = np.random.binomial(n=10, p=0.5, size=1000)
📍 np.random.binomial(n=10, p=0.5, size=1000)
➖ binomial: 이항분포에서 난수로 생성
➖ n: 시행 횟수 10
➖ p: 성공 확률이 0.5
➡️ 성공 확률이 0.5인 이항분포에서 시행 횟수가 10인 실험을 1000번 수행해 그 결과를 난수로 생성하겠다는 의미
# 히스토그램으로 시각화
plt.hist(binom_dist, bins=10, density=True, alpha=0.6, color='y')
plt.title('이항 분포 히스토그램')
plt.show()- 푸아송 분포

[푸아송 분포란?]
➖ 단위 시간 또는 단위 면적 당 발생하는 사건의 수를 모델링할 때 사용하는 분포
➖ 평균 발생률 λ를 가진 사건이 주어진 시간 또는 공간 내에서 몇 번 발생하는지를 나타냄
➖ 이항 분포처럼 연속된 값을 가지지 않기 때문에 이 분포도 이산형 분포에 해당
[특징]
➖ 푸아송 분포는 단위 시간 또는 단위 면적당 희귀하게 발생하는 사건의 수를 모델링하는 데 적합
➖ 평균 발생률이란 주어신 시간이나 공간에서 사건이 몇 번 발생했는지
➖ 한 시간동안 콜센터에 전화오는 건수가 10건이면 λ는 10
⭐️ 평균 발생률 λ가 충분히 크다면 정규분포에 근사
[파이썬 실습]
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# 푸아송 분포 파라미터 설정
lambda_value = 4 # 평균 발생률
x = np.arange(0, 15) # 사건 발생 횟수 범위
# 푸아송 분포 확률 질량 함수 계산
poisson_pmf = poisson.pmf(x, lambda_value)
# 그래프 그리기
plt.figure(figsize=(10, 6))
plt.bar(x, poisson_pmf, alpha=0.6, color='b', label=f'Poisson PMF (lambda={lambda_value})')
plt.xlabel('Number of Events')
plt.ylabel('Probability')
plt.title('Poisson Distribution')
plt.legend()
plt.grid(True)
plt.show()