위 주제는 밑바닥부터 시작하는 딥러닝2 5강, CS224d를 바탕으로 작성한 글 입니다.

오늘은 드디어 RNN!
순환 신경망 (Recurrent Neural Network)은 Squential Data처리에 적합한 모델이다.

Sequential Data란?

Sequential Data는 데이터와 데이터가 나타난 위치가 중요한 데이터를 말한다.

우리가 흔히 알고있는 대부분의 데이터들을 Squential Data라고 부르는데, 예로 Speech, Text, Image 데이터들이 Sequential Data라 할 수 있다.

우리가 주식데이터를 가지고 있다고 생각해보자.

데이터 1: 2000 2050 2100 2150 (상승)
데이터 2: 2150 2100 2050 2000 (하락)

여기서 데이터 1과 2에 있는 2100이라는 숫자가 같은 의미를 가지고 있을까?

상승하는 2100과 하락하는 2100은 의미가 다를 것이다. 다시말하면 2100이 "있다/없다"가 중요한 것이 아니라
2100의 위치는 어디에 있는지, 2100의 앞/뒤에는 어떤 숫자가 있는지가 중요한 것이다.

하나 더 예를 들어서 이미지를 보자.

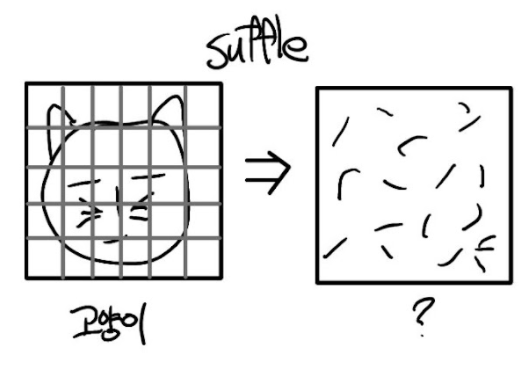
고양이 그림이 픽셀 단위로 Suffle 되면 우리는 저 그림을 고양이라고 하지 않을 것이다.
Suquential Data는 어떤 데이터가 있는가 없는가도 중요하지만 어떠한 순서로 되어있는가도 매우 중요하다.

RNN 등장 배경

우리는 지금까지 피드포워드라는 유형의 신경망을 공부하였다.
피드포워드란

• 흐름이 단방향인 신경망
• 입력 신호가 다음 층(중간층)으로 전달되고, 그 신호를 받은 층은 그 다음 층으로 전달하고, 다시 다음층으로.. 이런식으로 한 방향으로만 신호가 전달된다.
• 구성이 단순하고 구조를 이해하기 쉽다.
• 시계열 데이터를 잘 다루지 못한다는 단점이 있다.
  • 시계열 데이터의 패턴을 충분히 학습 할 수 없다.
  • 패턴도 충분히 학습할 수 있는 RNN이 등장!

확률 관점에서 보자

이전에 word2vec부분에서 확률의 관점에서 바라볼 수 있다 했다.

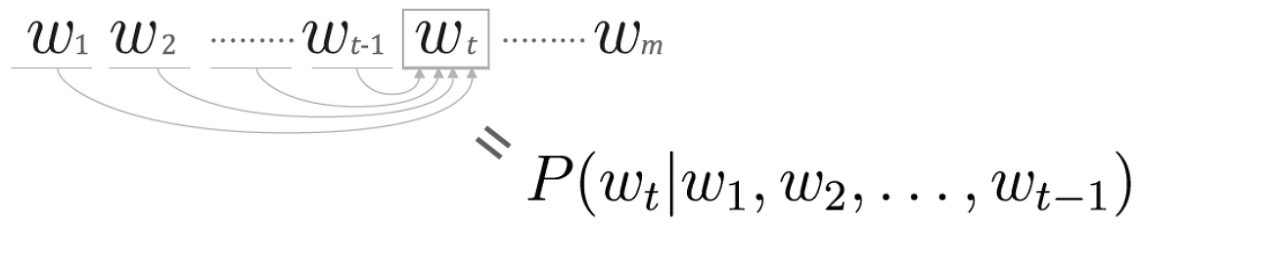
"w1 부터 wt+1까지 주어졌을 때 wt가 일어날 확률"이다.
그런데, 우리는 window_size를 주어서 맥락을 좌우 대칭으로 생각해 왔다. 그림이 맥락을 왼쪽으로만 되어있어서 헷갈릴 수 있는데, 이유는 '언어 모델'에서 설명한다.

언어 모델(Language model)

언어 모델은 단어 나열에 확률을 부여해서 특정 단어 시퀀스에 대해서 그 시퀀스가 일어날 확률을 확인한다.

즉, 문장이 얼마나 자연스러운가를 본다.

"I say goodbye"하면 확률이 높지만, "You say good die"라면 확률이 당연 낮아진다.

이를 통해 어떤 답변이 자연스러운 흐름인지 확률을 통해 답변을 내놓을 수 있다.

언어 모델에서 가장 중요한 점은 확률이 타깃 단어보다 왼쪽에 있는 모든 단어를 맥락으로 했을 때 나타난다는 것이다.

w1, w2, ..., wm이라는 m개의 단어로 된 문장을 생각해보자.

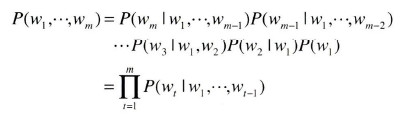
파이 기호는 '총곱'을 의미한다. 위 식은 확률의 곱셈공식 P(A, B) = P(A|B)P(B)을 사용해서 식 변형을 수행할 수 있다.

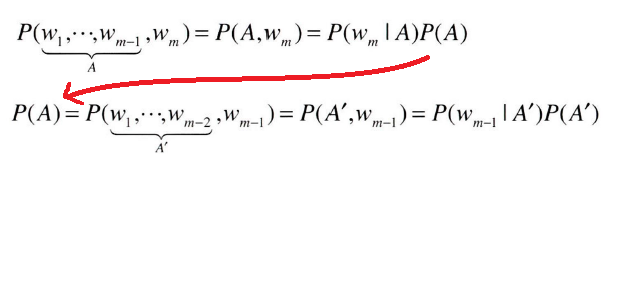
식을 통해서 동시확률 P(w1,...,wm)은 타깃 단어 보다 왼쪽에 있는 모든 단어를 맥락(조건)으로 했을 때의 확률이라는 것을 알 수 있다.

맥락을 왼쪽으로 사용하는 이유를 이해할 수 있다.

CBOW 모델을 언어 모델로?

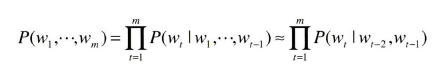
CBOW 모델은 윈도우의 크기를 고려하여 근사적으로 나타낼 수 있다.
그러다 보니, window_size 밖에 있는 단어의 정보는 무시된다.

Tom was watching tv in his room, mary came into the room. mary said hi to ????

???에 들어갈 말은 "Tom"일 확률이 높다. 근데 Tom은 ???에서 너무 멀리 있어 Cbow는 "Tom"을 못볼 수 있다.
사이즈를 늘리면 될까?

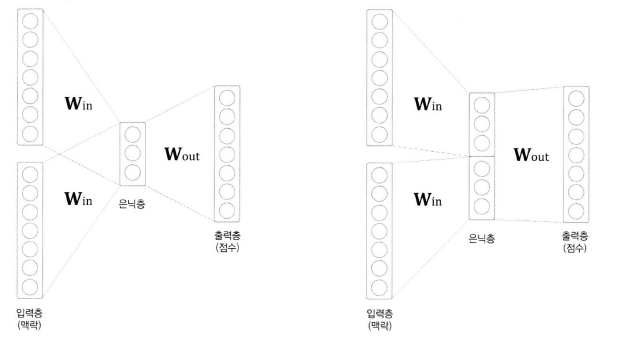
윈도우 사이즈를 크게해서 본다해도 모델을 생각해보면 왼쪽 그림 처럼 입력층의 벡터를 평균내서 계산하기때문에 앞의 단어들의 순서를 모두 무시하게 된다.

(you, say)와 (say, you)를 같은 맥락으로 취급하면 성능이 안좋을 확률이 높다.

이를 해결하기 위해서 처음에는 오른쪽 그림처럼 벡터들을 연결(concatenate)하는 방법을 생각했는데 이렇게 하면 벡터가 너무 길어지게 되고 매개변수가 많아진다. 따라서 최종 해결책인 RNN을 이용하게 되었다.

기존의 word2vec모델을 사용하면 맥락을 파악하기 힘들어 시계열 데이터를 사용한 예측에 문제가 있었고, 이를 해결하기 위해서 RNN모델을 사용한다. word2vec은 자연어의 분산표현을 얻기위해서 사용된다고 기억하자.

RNN

RNN의 '순환'에는 어떤 의미가 있을까? 물론 '반복해서 되돌아감'을 의미한다. RNN을 살펴보자.

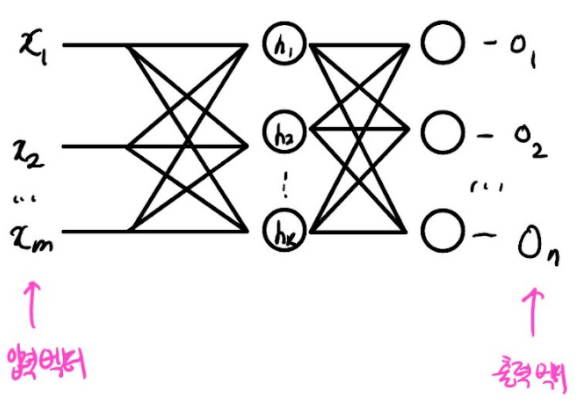
흔한 Fully Connected Layer이다. 입력벡터로 들어가서 layer를 지나 출력 벡터를 꺼내는 방식이다.

여기에 C1,C2,Ck Layer를 추가해보자.

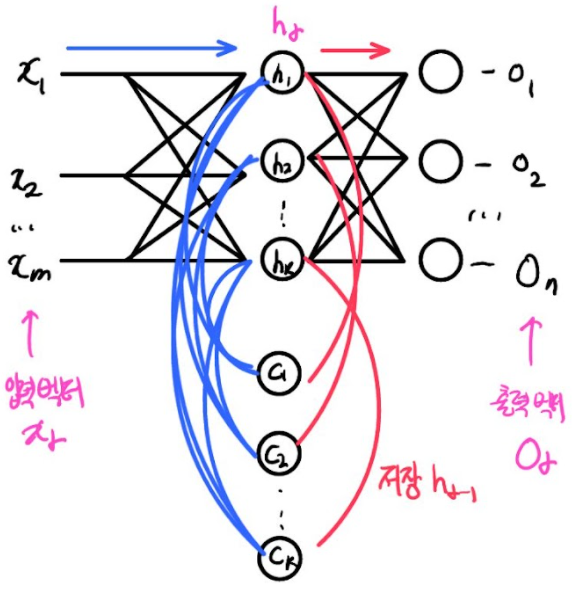
C1, C2 ... Ck 레이어는 matmul, activation등등 processing을 진행하는 노드들과는 다르게 단지 버퍼, 메모리 어떤 값을 저장하는 용도로 쓰인다.

h1, h2 ... hk 의 값을 c1, c2에 저장한다.

간단하게 동작 순서를 설명하면,

• 입력 벡터 원소, 하나의 입력이 들어가면 이에 대응하여 hidden layer의 결과(h1, h2 ... hk)가 일어난다.

• h는 output을 위해 다음 계층으로 전달된다.
  h을 copy하여 c1, c2 ... ck에 저장한다. (h1)

• 2번째 입력 벡터 원소를 입력하면, x1, x2 ... xm만 들어가는 것이 아니라,
  전에 저장해 놓았던 c1, c2 ... ck 값이 hidden layer에 들어간다.

• h는 output을 위해 다음 계층으로 전달된다.
  h을 copy하여 c1, c2 ... ck에 저장한다. (h2)

... 반복

C의 초기값은 0으로 해도 되고, 랜덤값으로 주어도 된다.
참고로 첫번째 입력 벡터 원소에 입력할 때에도 사실 C값(초깃값)이 사용된다.

이를 쉽게 블럭으로 바꾸면

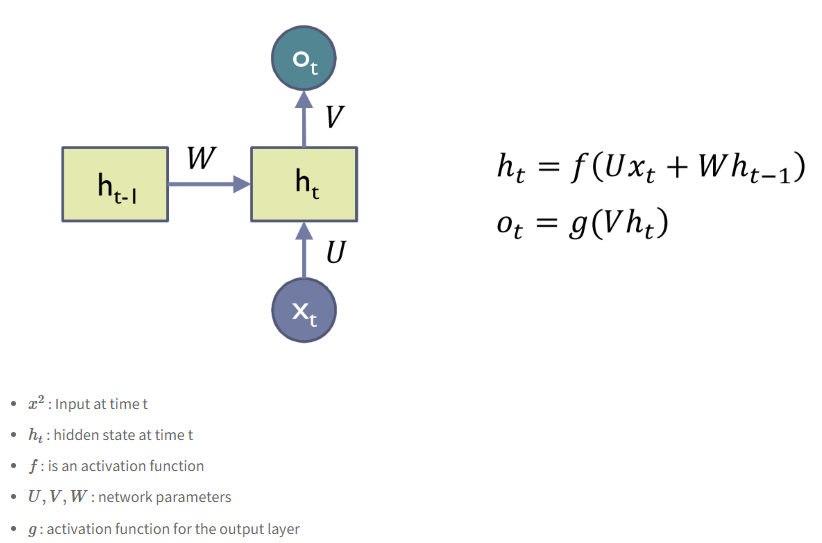
이렇게 표현할 수 있다. 이렇게 보니 단순 Neural Network인게 보인다.

문장을 단어로 바꾸어서 생각해보았을 때,
train 데이터는 (x0, h0), (x1, h1), (x2, h2) ... (xt, ht) 이를 시계열 데이터로 사용할 수 있다.

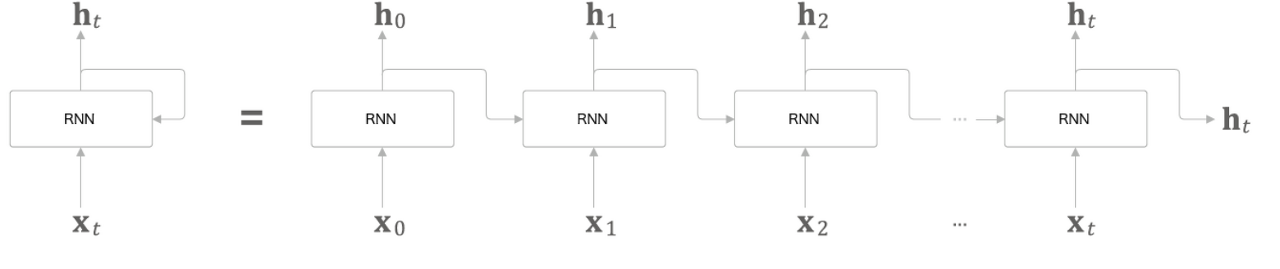
RNN 계층의 순환 구조를 펼침으로써 오른쪽으로 긴 신경망으로 변신 시킬 수 있다.
그림에서 등장하는 RNN들 모두가 실제로는 '같은 계층'인 것이 지금까지 신경망과는 다르다.

RNN의 수식은 다음과 같다.

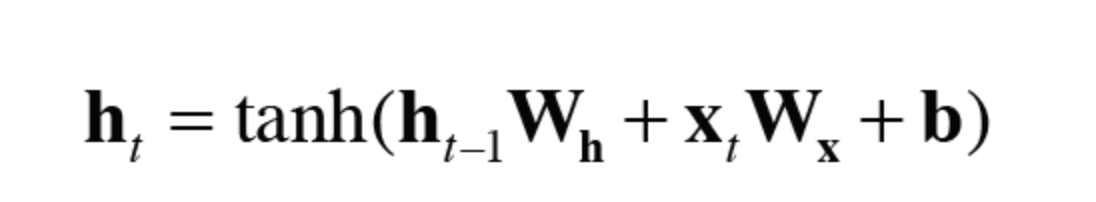
• h는 hidden state vector이라고 표현한다. (은닉 상태 벡터)
• 행렬곱을 계산하면 그 합을 tanh함수를 이용해 변환한다.

BPTT

BPTT는 '시간 방향으로 펼친 신경망의 오차역전파법' (Backpropagation Through Time)을 의미한다.

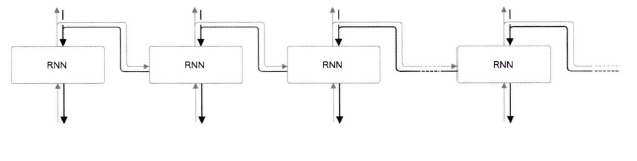
이전 모델과 같이 순전파를 수행하고, 이어서 역전파를 수행하여 원하는 기울기를 구할 수 있다.
여기서 사용하는 오차역전파 법이 BPTT이다. 하지만 긴 시계열 데이터 학습할 때 문제가 생긴다.

바로 역전파 과정에서 상당한 컴퓨팅 메모리를 사용한다는 것과, 너무 Sensitive한 gradient를 얻는 다는 것이다.

BPTT 문제점

RNN은 Long Term Dependency를 잘 모델링 하지 못한다.

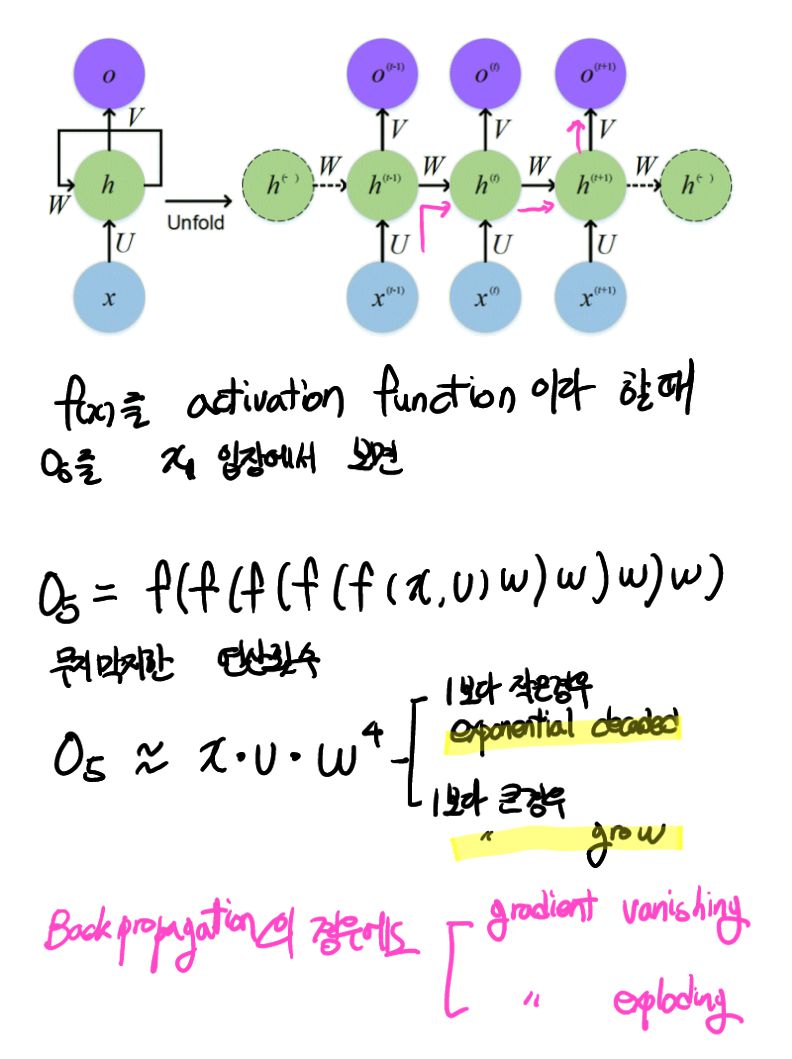
만약에 O5를 구하려고 W의 값을 조정하면 너무 sensitive해서 exponential decay로 W이 0이 되어 소멸하거나,
exponential growth로 기하급수적으로 증가할 것이다.

Truncated BPTT

그래서 해결 방법이 신경망 연결을 적당한 길이로 '끊는 것'인데, '역전파'의 연결만 끊어 블록단위로 학습을 하는 것이 포인트이다.

만약 1,000개의 시계열 데이터가 있다고 한다면, RNN 계층이 1,000개나 늘어선 신경망이 된다.

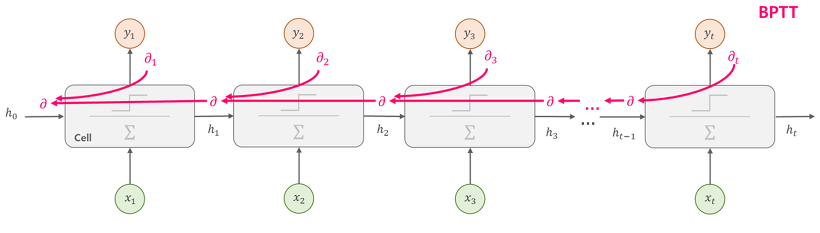
기존 BPTT로 하면 당연히 방금 언급한 것과 같은 문제가 생긴다.

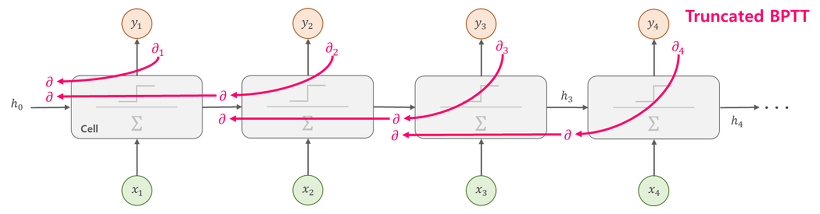
그래서 역전파의 연결을 단위로 끊어서 학습하게된다. 이러면 단위보다 미래의 데이터에 대해서는 생각할 필요가 없어진다.

즉 블록으로 만들어, 독립적으로 오차역전파법을 시킨다.

중요한점은 순전파 연결은 끊지 않는다는 것이다. 이는 데이터를 순서대로 입력한다는 것을 말한다.

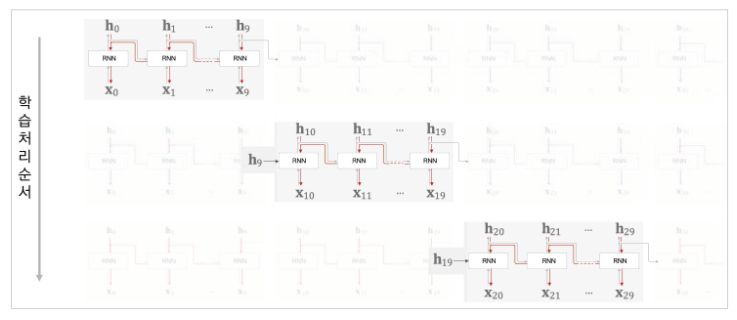
가중치 갱신은 첫 번째 블록이 블록 내부에서 순전파를 실행하고

역전파 과정을 거쳐서 기울기를 바탕으로 갱신 된 가중치 조건들이

두 번째 블록의 가중치 초기 조건으로 사용된다.

마찬가지로 두 번째 블록의 계층들이 해당 초기 가중치 조건으로 순전파를 진행한 후

다시 끝에서 처음까지(블록 안 기준) 역전파를 해서 갱신된 가중치 조건들이

세 번째 블록의 가중치 초기 조건으로 사용된다.

이런식으로 반복이되고 이를 통해 기존 블록의 갱신된 가중치가 다음 블록으로 넘어가서 실행되고 갱신되므로 역전파를 끊어서 사용해도 학습에 크게 지장이 없다는 것을 알 수 있다.

미니배치 학습

지금까지의 설명은 미니배치 수가 1일 때를 설명했다.
미니배치 학습이 좋은 측면이 있어서, 미니 배치를 하기위해 데이터를 주는 시작 위치를 각 미니 배치의 시작 위치로 '옮겨줘야'한다.

'옮긴다'라는 뜻을 길이가 1000인 시계열 데이터에 대해서 시각의 길이를 10개 단위로 잘라 Truncated BPTT로 학습하는 경우를 예로한다.

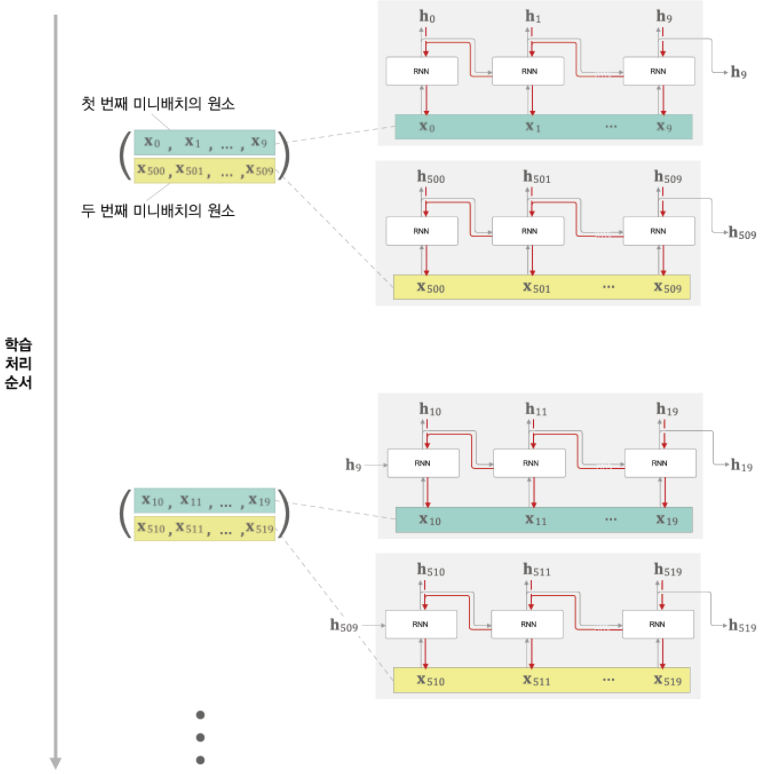
미니배치 수를 2개로 구성한다고 하면,

첫 번째 미니 배치 때는 0번부터 순서대로 499번 까지 10개씩 묶을 것이다.(50 묶음)

두 번째 미니 배치 때는 500번째 데이터를 시작으로 999번까지 10개씩 묶어 (50 묶음) 배치의 수가 2개인 데이터를 만든다.

그리고 미니 배치별로 데이터를 제공하는 시작위치를 옮겨준다.

이처럼 미니배치 학습을 수행할 때는
1. 각 미니배치의 시작 위치를 오프셋으로 옮겨준 후 순서대로 제공하면 된다.
2. 데이터를 순서대로 입력하다 끝에 도달하면 다시 처음부터 입력하도록 한다.

다음글로는 직접 RNN을 구현해보고 여러 RNN을 묶음으로 하는 Time RNN도 구현해 본다. 그리고 시계열 데이터 처리 계층 구현도 해본다.