백준 29715번 : 비밀번호 찾기

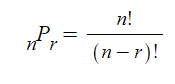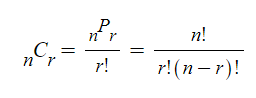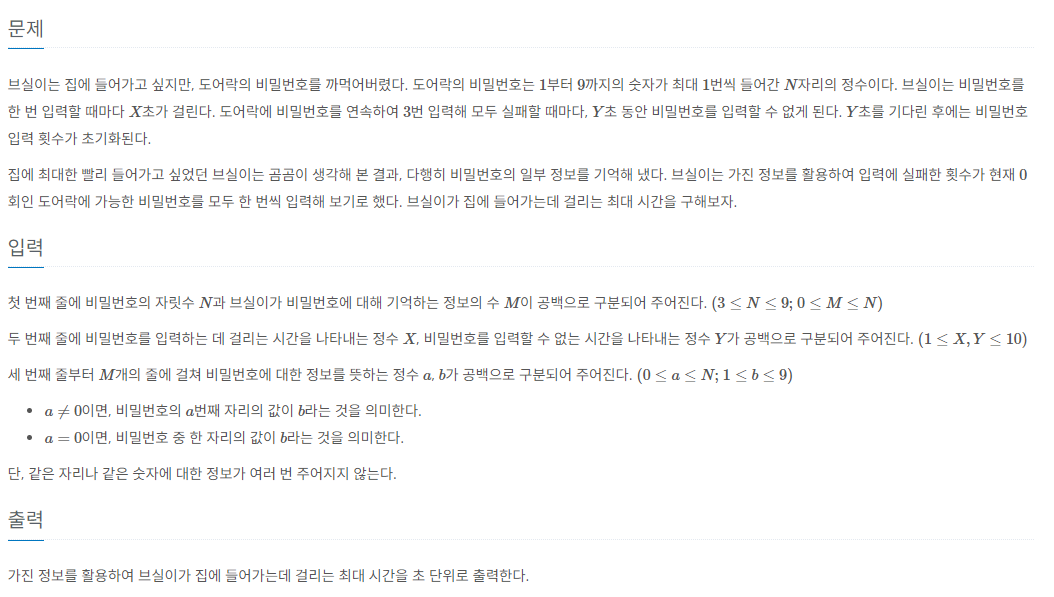
• 문제 선정 이유 : 알고리즘 문제 해결 재활 용 낮은 난이도 문제 풀이
• Solved.ac 기준 실버 3
• 사용언어 C++

문제 해석

1. 빈 자리에 숫자를 배치할 수 있는 경우의 수를 찾는 문제
2. 문제의 예시로 설명하면 4자리 숫자의 2ㅁㅁ8이라는 위치와 값을 모두 알고 있는 숫자들은 고려하지 않고 남은 자리에 숫자가 들어가는지 여부를 판단
3. 빈 곳에 들어갈 숫자가 제공 된다면 배치 관련 경우의 수만 고려
4. 경우의 수와 중간 대기 시간을 고려하여 답 도출

문제 풀이

1. 결국 이미 위치와 값을 아는 입력은 고려할 필요 없음
2. 숫자를 아는 경우와 모르는 경우로 나눠 고려하여 계산
3. 조합과 순열을 고려하면 쉬움

※ 조합과 순열

조합

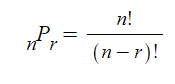
순열

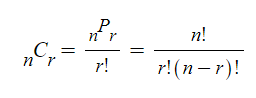
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

int n, m;
int x, y;

long long comb(int a, int b) {																					// 조합
	if (b > a) return 0;																				
	if (b * 2 > a) b = a - b;																							
	if (b == 0) return 1;																								

	long long res = a;
	for (int i = 2; i <= b; i++) {
		res *= (a - i + 1);
		res /= i;
	}
	return res;
}

long long perm(int a, int b) {																						// 순열
	if (b > a) return 0;
	long long res = 1;
	for (int i = 0; i < b; i++) {
		res *= (a - i);
	}
	return res;
}

int main() {
	cin.tie(NULL);
	ios_base::sync_with_stdio(false);

	cin >> n >> m;
	cin >> x >> y;

	int setPW = 0;																										// 자리수가 주어진 비밀번호
	int noneSetPW = 0;																								// 자리수가 주어지지 않은 비밀번호

	for (int i = 0; i < m; i++) {
		int a, b;
		cin >> a >> b;

		if (a != 0) {
			setPW++;	
		}
		else {
			noneSetPW++;
		}
	}

	n -= setPW;																											// 자리수가 주어진 비밀번호는 계산에서 제외

	long long result = 1;

	if (noneSetPW > 0) {
		result *= comb(n, noneSetPW) * perm(noneSetPW, noneSetPW);						// 조합(자릿수, 자리가 정해지지 않은 수) * 순열(자리가 정해지지 않은 수, 자리가 정해지지 않은 수)
	}

	n -= noneSetPW;

	if (n > 0) {
		result *= perm(9 - (setPW + noneSetPW), n);													// 순열(9 - (자리가 정해진 수 + 자리가 정해지지 않은 수), 자릿수)
	}

	cout << result * x + (result - 1) / 3 * y;																	// 결과 * 입력하는데 걸리는 시간 + (결과 - 1) / 3 * 입력 잠금 시간
	

	return 0;
}