Decision tree

u8cnk1·2023년 7월 14일

의사결정 트리(decision tree)

: 어떤 항목에 대한 관측값과 목표값을 연결시켜주는 예측 모델로써 결정 트리를 사용하는 머신러닝 방법
→ 영향력이 큰 특징을 상위 노드로, 영향력이 작은 특징은 하위 노드로 선택한다.
→ 특징 별 영향력의 크고 작음을 비교하기 위해 엔트로피와 정보 이득을 이용

장점

수학적인 지식이 없어도 결과를 해석하고 이해하기 쉬움

수치 데이터 및 범주 데이터에 모두 사용 가능

정확도가 비교적 높은편

단점

과대적합의 위험성이 높음

최적의 솔루션을 보장하지 않음

학습과 시각화

붓꽃 데이터셋 이용하여 DecisionTreeClassifier 훈련시키기

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier

iris = load_iris()
X = iris.data[:, 2:] # 꽃잎 길이와 너비
y = iris.target

tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X, y)

export_graphviz() 함수 이용하여 붓꽃 결정 트리 시각화

from graphviz import Source
from sklearn.tree import export_graphviz

export_graphviz(
        tree_clf,
        out_file=os.path.join(IMAGES_PATH, "iris_tree.dot"),
        feature_names=iris.feature_names[2:],
        class_names=iris.target_names,
        rounded=True,
        filled=True
    )

Source.from_file(os.path.join(IMAGES_PATH, "iris_tree.dot"))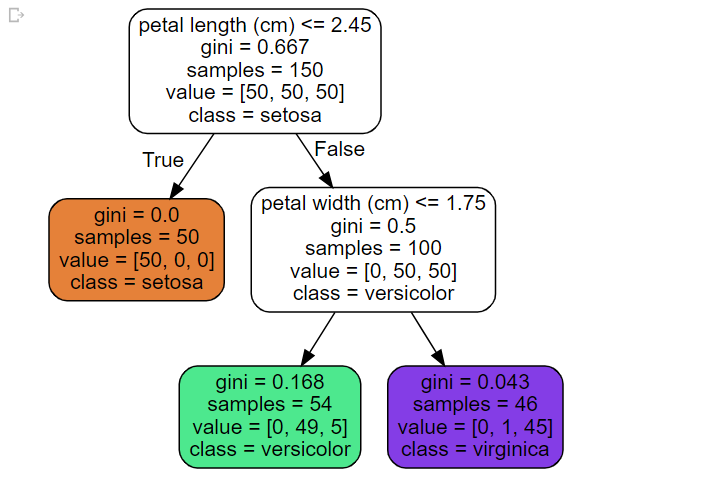

예측하기

새로 발견한 붓꽃의 품종 분류

루트노드 - 꽃잎의 길이가 2.45cm보다 짧은지 검사한다.
- 만약 그렇다면 루트 노드에서 외녹 자식 노드로 이동, 리프 노드이므로 추가적인 검사를 하지 않는다. → 새로 발견한 꽃의 품종을 Iris-Setosa라고 예측
- 꽃잎의 길이가 2.45cm보다 길다면 오른쪽 자식 노드로 이동, 추가적으로 꽃잎의 너비가 1.75cm보다 작은지 검사한다.
  - 만약 그렇다면 Iris-Versicolor, 그렇지 않다면 Iris-Virginica로 예측한다.

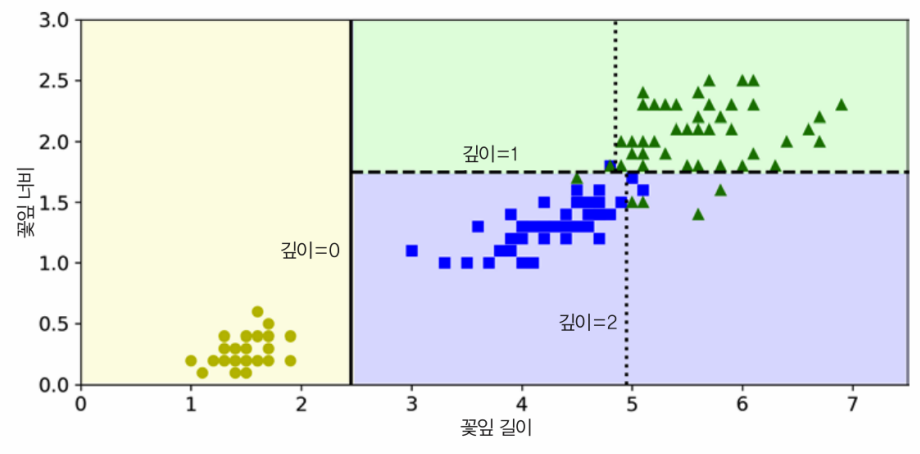
위 그림은 이 decision tree의 결정 경계를 보여준다. 굵은 수직선이 루트 노드의 결정 경계(꽃잎 길이=2.45cm)를 나타낸다. 왼쪽 영역은 순수 노드(Iris-Setosa만 있음)이기 때문에 더 이상 나눌 수 없다.

하지만 오른쪽 영역은 순수 노드가 아니므로 오른쪽 노드는 꽃잎 너비=1.75cm에서 나누어진다.

max_depth를 2로 설정했기 때문에 더 이상 분할되지 않는다.
(max_depth를 3으로 하면 깊이가 2인 두 노드가 각각 결정 경계(점선)를 추가로 만든다.)

클래스 확률 추정

decision tree는 한 샘플이 특정 클래스 k에 속할 확률을 추정할 수 있다.
먼저 이 샘플에 대해 리프 노드를 찾기 위해 트리를 탐색하고 그 노드에 있는 클래스 k의 훈련 샘플의 비율을 반환한다.

예를 들어 길이가 5cm이고 너비가 1.5cm인 꽃잎을 가정하면, 이에 해당하는 리프 노드는 깊이 2에서 왼쪽 노드이므로 decision tree는 그에 해당하는 확률을 출력한다.
즉, Iris-Setosa는 0%(0/54), Iris-versicolor는 90.7%(49/54), Iris-Virginica는 9.3%(5/54)이다. 클래스를 하나 예측한다면 가장 높은 확률을 가지는 Iris-Versicolor(클래스 1)를 출력할 것이다.

CART 훈련 알고리즘

사이킷런은 decison tree를 훈련시키기 위해(트리를 성장시키기 위해) CART(classification and regression tree) 알고리즘을 사용한다.

사이킷런의 의사결정 트리는 CART 타입의 트리(이진 분류) → 이진 트리인 CART 타입의 트리를 분류할 때 지니 계수를 사용한다.
(지니 계수가 높을수록 순도가 높음)

먼저 훈련 세트를 하나의 특성 k의 임곗값을 사용해 두 개의 서브셋으로 나눈다.(예: 꽃잎의 길이 <= 2.45cm)
이때 가장 순수한 서브셋으로 나눌 수 있는 특성과 임곗값의 쌍을 찾는다. 이 알고리즘이 최소화해야 하는 비용 함수의 식은 다음과 같다.

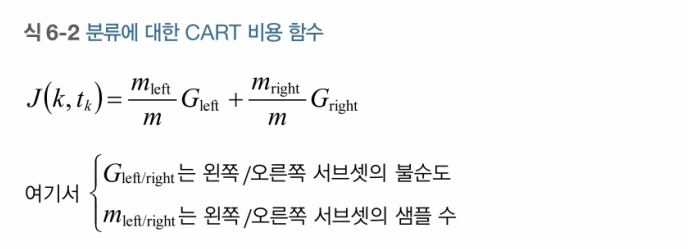
CART 알고리즘이 훈련 세트를 성공적으로 둘로 나누었다면 같은 방식으로 서브셋을 나누는 과정을 반복한다. 이 과정은 max_depth 매개변수로 정의된 최대 깊이가 되면 중지하거나 불순도를 줄이는 분할을 찾을 수 없을 때 멈추게 된다.

계산 복잡도

예측을 하려면 트리를 루트 노드에서부터 리프 노드까지 탐색해야 한다. 일반적으로 decision tree는 거의 균형을 이루고 있으므로 트리를 탐색하기 위해서는 약 $O(\log_{2}{(m)})$ 개의 노드를 거쳐야 한다. 각 노드는 하나의 특성값만 확인하기 때문에 예측에 필요한 전체 복잡도는 특성 수와 무관하게 $O(\log_{2}{(m)})$ 가 된다. 그래서 큰 훈련 세트를 다룰 때도 예측 속도가 매우 빠르다.

훈련 알고리즘은 각 노드에서 모든 훈련 샘플의 모든 특성을 비교한다. 각 노드에서 모든 샘플의 모든 특성을 비교하면 훈련 복잡도는 $O(n\times m\log_{2}{(m)})$ 이 된다. 훈련 세트가 (수천 개 이하의 샘플 정도로) 작을 경우 사이킷런은 (presort=True로 지정하면) 미리 데이터를 정렬하여 훈련 속도를 높일 수 있다. 하지만 훈련 세트가 클 경우에는 속도가 많이 느려진다.

지니 불순도 / 엔트로피

기본적으로 지니 불순도가 사용되지만 criterion 매개변수를 "entropy"로 지정하여 엔트로피 불순도를 사용할 수도 있다. 엔트로피는 분자의 무질서함을 측정하는 것으로 원래 열역학의 개념이지만(분자가 안정되고 질서 정연하면 엔트로피가 0에 가깝다.) 머신러닝에서는 불순도의 측정 방법으로 자주 사용된다. 어떤 세트가 한 클래스의 샘플만 담고 있다면 엔트로피가 0이다.
$i$ 번째 노드의 엔트로피 정의는 다음과 같다.

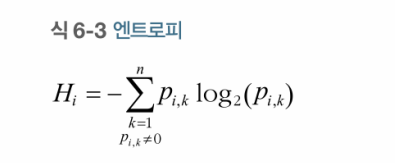
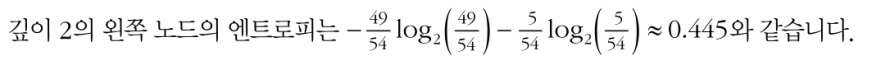
지니 불순도와 엔트로피 중 어떤 것을 사용해도 비슷한 트리를 만들어낸다. 지니 불순도가 조금 더 계산이 빠르기 때문에 기본값으로 좋지만, 다른 트리가 만들어지는 경우 지니 불순도가 가장 빈도 높은 클래스를 한쪽 가지(branch)로 고립시키는 경향이 있는 반면 엔트로피는 조금 더 균형 잡힌 트리를 만든다.

규제 매개변수

선형 모델은 데이터가 선형일 거라 가정하는 반면, 결정 트리는 훈련 데이터에 대한 제약 사항이 거의 없다.

그러나 제한을 두지 않으면 트리가 훈련 데이터에 아주 가깝게 맞추려고 해서 대부분 overfitting 되기 쉽다. 결정 트리는 모델 파라미터가 전혀 없는 것이 아니라 훈련되기 전에 파라미터 수가 결정되지 않기 때문에 이런 모델을 비파라미터 모델(nonparametric model)이라고 부른다. 그래서 모델 구조가 데이터에 맞춰져서 고정되지 않고 자유롭다.

반대로 선형 모델 같은 파라미터 모델(parametric model)은 미리 정의된 모델 파라미터 수를 가지므로 자유도가 제한되고 overfitting될 위험이 줄어든다.

훈련 데이터에 대한 과대적합을 피하기 위해 학습할 때 결정 트리의 자유도를 제한(규제)할 필요가 있다. 규제 매개변수는 사용하는 알고리즘에 따라 다르지면, 보통 decision tree의 최대 깊이는 제어할 수 있다. → 사이킷런에서는 max_depth 매개변수로 이를 조절한다. (max_depth를 줄이면 모델을 규제하게 되고 과대적합의 위험이 감소한다.)

DecisionTreeClassifier에는 비슷하게 결정 트리의 형태를 제한하는 다른 매개변수가 있다.

min_samples_split : 분할되기 위해 노드가 가져야 하는 최소 샘플 수
min_samples_leaf : 리프 노드가 가지고 있어야 할 최소 샘플 수
min_weight_fraction_leaf : min_samples_leaf와 같지만 가중치가 부여된 전체 샘플에서의 비율
max_leaf_nodes : 리프 노드의 최대 수
max_features : 각 노드에서 분할에 사용할 특성의 최대 수

→ min-으로 시작하는 매개변수를 증가시키거나 max_로 시작하는 매개변수를 감소시키면 모델에 규제가 커진다.

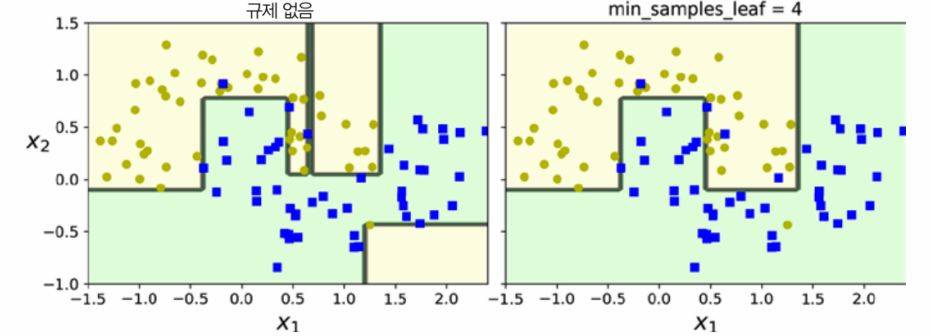
위 그림에서 왼쪽 결정 트리는 규제가 없는 기본 매개변수를 사용하여 훈련시켰고, 오른쪽 결정 트래는 min_samples_leaf를 4로 지정하여 훈련시킨 결괴이다. 왼쪽 모델은 확실히 과대적합되었고 오른쪽 모델은 일반화 성능이 더 좋을 것이다.

참고) 제한 없이 결정 트리를 훈련시키고 불필요한 노드를 가지치기 pruning하는 알고리즘도 있다. 순도를 높이는 것이 통계적으로 큰 효과가 없다면 리프 노드 바로 위의 노드는 불필요할 수 있다. 이 확률을 'p-값'이라 부르며 통상적으로 5%보다 높으면 그 노드는 불필요한 것으로 간주되고 그 자식 노드는 삭제된다. 가지치기는 불필요한 노드가 모두 없어질 때까지 계속된다.

회귀

사이킷런의 DecisionTreeRegressor를 사용하여 회귀 문제에도 decision tree를 사용할 수 있다.

# 2차식으로 만든 데이터셋 + 잡음
np.random.seed(42)
m = 200
X = np.random.rand(m, 1)
y = 4 * (X - 0.5) ** 2
y = y + np.random.randn(m, 1) / 10

잡음이 섞인 2차 함수 형태의 데이터셋에서 'max_depth=2' 설정으로 회귀 트리를 만든다.

from sklearn.tree import DecisionTreeRegressor

tree_reg = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg.fit(X, y)

앞의 분류 트리와 비슷하지만, 회귀 결정 트리의 경우 각 노드에서 클래스를 예측하는 대신 어떤 값을 예측한다.

u8cnk1

이전 포스트

모델 훈련

다음 포스트