선형 회귀

일반적으로 선형 모델은 입력 특성의 가중치 합과 편향이라는 상수를 더해 예측을 만든다.

이 식은 벡터 형태로 더 간단하게 쓸 수 있다.

모델 훈련 ⇒ 모델이 train set에 가장 잘 맞도록 모델 파라미터를 설정하는 것, 이를 위해 먼저 모델이 train data set에 얼마나 잘 맞는지 측정해야 한다.

• 선형 회귀 모델을 훈련시키려면 RMSE(또는 MSE)를 최소화하는 θ를 찾아야 한다.
  

정규방정식

= 비용 함수를 최소화하는 θ값을 찾기 위한 해석적인 방법(수학 공식)

경사 하강법

gradient descent

여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘으로, 비용 함수를 최소화하기 위해 반복해서 파라미터를 조정한다.

파라미터 벡터 θ 에 대해 비용 함수의 현재 gradient를 계산하여 gradient가 감소하는 방향으로 진행한다. → gradient가 0이 되면 최솟값에 도달한 것

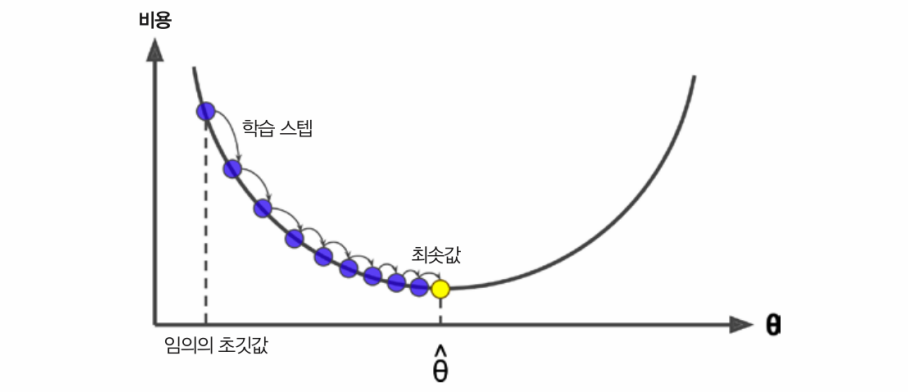
그림에서와 같이 모델 파라미터가 무작위하게 초기화(임의의 값으로 시작)된 후 반복적으로 수정되어 비용 함수를 최소화한다.
( 학습 step 크기는 비용 함수의 기울기에 비례, 파라미터가 최솟값에 가까워질수록 step 크기가 점진적으로 줄어든다. )

경사 하강법에서 중요한 파라미터는 step의 크기로, learning rate 하이퍼파라미터로 결정된다.

• learning rate 가 너무 작으면 알고리즘이 수렴하기 위해 반복을 많이 진행해야 하므로 시간이 오래 걸린다.
  

• 반면 learning rate가 너무 크면 골짜기를 가로질러 반대편으로 건너뛰게 되어 이전보다 더 높은 곳으로 올라가게 될 수 있다. 이는 알고리즘을 더 큰 값으로 발산하게 만들어 적절한 해법을 찾지 못하게 될 수 있다.
  

경사 하강법의 문제점

θ 가 무작위로 초기화되기 때문에 알고리즘이 global minimum이 아닌, local minimum에 수렴할 수 있다.

선형 회귀를 위한 MSE 비용 함수는 local minimum이 없고 하나의 global minimum만을 가지는 볼록 함수이므로, learning rate가 너무 크지 않고 충분한 시간이 주어지면 경사 하강법이 global minimum에 가깝게 접근할 수 있다는 것을 보장한다.

※ 경사 하강법을 사용할 때에는 사이킷런의 StandardScaler 등을 사용하여 모든 특성이 같은 스케일을 갖도록 해야 한다.

배치 경사 하강법

batch gradient descent

경사 하강법을 구현하려면 각 모델 파라미터 θ j에 대해 비용 함수의 gradient, θ j가 조금 변경될 때 비용함수가 얼마나 바뀌는지(→ 편도함수, partial derivative)를 계산해야 한다.

각 파라미터의 편도함수를 각각 계산하는 대신 gradient 벡터를 사용하여 한꺼번에 계산할 수 있다.

이 공식은 매 경사 하강법 step에서 전체 훈련 세트 X에 대해 계산한다. ▷ batch gradient descent

gradient 벡터가 구해지면, step의 크기를 결정하기 위해 learning rate를 곱하고 θ 에서 그 값을 뺀다.

적절한 learning rate를 찾기 위해 그리드 탐색을 사용할 수 있다. 하지만 그리드 탐색에서 수렴하는 데 너무 오래 걸리는 모델을 막기 위해 반복 횟수를 제한해야 한다. → 반복 횟수를 아주 크게 지정하고 gradient 벡터가 아주 작아지면, 즉 벡터의 노름이 어떤 값 ε(허용오차)보다 작아지면 경사 하강법이 거의 최솟값에 도달한 것이므로 알고리즘을 중지한다.

확률적 경사 하강법

• 배치 경사 하강법 : 매 step에서 전체 train 세트를 사용해 gradient를 계산하므로 train 세트가 커지면 매우 느려진다.
• ↔ 확률적 경사 하강법 : 매 step에서 한 개의 샘플을 무작위로 선택하고 그 하나의 샘플에 대한 gradient를 계산, 매 반복에서 다뤄야 할 데이터가 매우 적기 때문에 한 번에 하나의 샘플을 처리하고 알고리즘이 훨씬 빠르다.

확률적 경사 하강법을 사용하면 개별 훈련 스텝은 매우 빠르지만 배치 경사 하강법을 사용할 때보다 훨씬 확률적(무작위)이 된다.

확률적 경사 하강법을 사용할 때 훈련 샘플이 IID(independent and identically distributed)를 만족해야 평균적으로 파라미터가 global minimum을 향해 진행한다고 보장할 수 있다.

미니 배치 경사 하강법

각 step에서 미니 배치라 부르는 임의의 작은 샘플 세트에 대해 gradient를 계산한다.

• 배치 경사 하강법 : 각 스텝에서 전체 훈련 세트에 대해 gradient 계신
• 확률적 경사 하강법 : 하나의 샘플을 기반으로 gradient 계산
• 미니 배치 경사 하강법 : 임의의 작은 샘플 세트에 대해 gradient 계산

early stopping

경사 하강법과 같은 반복적인 학습 알고리즘을 규제하는 방법으로, validation error가 최솟값에 도달하면 학습을 중지시킨다.
(에포크가 진행됨에 따라 알고리즘이 점차 학습되어 train set에 대한 test error와 validation set에 대한 test error가 줄어든다. 그러나 잠시 후 감소하던 validation error가 다시 증가하는데, 모델이 train data에 과대적합되기 시작하는 것을 의미한다.)

로지스틱 회귀

: 샘플이 특정 클래스에 속할 확률을 추정할 때 사용

확률 추정

선형 회귀 모델과 같이 입력 특성의 가중치 합을 계산하고 편향을 더한다. 대신 선형 회귀처럼 바로 결과를 출력하지 않고 결괏값의 로지스틱을 출력한다.

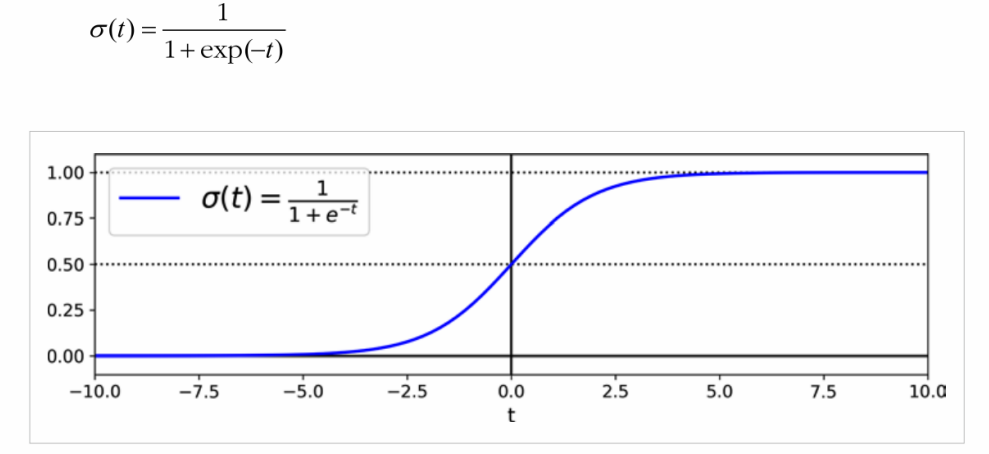
로지스틱(σ로 표시)은 0과 1 사이의 값을 출력하는 시그모이드 함수로 다음과 같이 정의된다.

사이킷런의 LogisticRegression은 클래스 레이블을 반환하는 predict() 메서드와 클래스에 속할 확률(시그모이드 함수를 적용하여 계산한 확률)을 반환하는 predict_proba() 메서드를 가지고 있다.

비용 함수

비용 함수가 볼록 함수이므로 learning rate가 너무 크지 않고 충분히 기다릴 시간이 있다면, 경사 하강법이 global minimum을 찾는 것을 보장한다.
이 비용 함수의 j번째 모델 파라미터 θ j 에 대해 편미분하면 다음 식과 같다.

각 샘플에 대해 예측 오차를 계산하고 j번째 특성값을 곱해 모든 훈련 샘플에 대해 평균을 낸다. 모든 편도함수를 포함한 gradient 벡터를 만들면 경사 하강법 알고리즘을 사용할 수 있다.

소프트맥스 회귀

로지스틱 회귀 모델은 여러 개의 이진 분류기를 훈련시켜 연결하지 않고 직접 다중 클래스를 지원하도록 일반화될 수 있다. → 소프트맥스 회귀, 다항 로지스틱 회귀

샘플 x가 주어지면 소프트맥스 회귀 모델이 각 클래스에 대한 점수를 계산하고, 그 점수에 소프트맥스 함수를 적용하여 각 클래스의 확률을 추정한다.

각 클래스의 점수가 계산되면 소프트맥스 함수를 통과시켜 클래스에 속할 확률을 추정한다.

로지스틱 회귀 분류기와 마찬가지로 추정 확률이 가장 높은 클래스(가장 높은 점수를 가진 클래스)를 선택한다.