[혼공머신]5주차_비지도 학습

군집 알고리즘

군집 알고리즘은 클러스터링이라고도 하는데, 비슷한 샘플들 끼리 모으는 비지도 학습이다. 책의 6장 1절에서는 비지도 학습은 아닌 지도 학습으로 사진의 각 픽셀별 평균값을 구해 그 평균과 가장 가까이 있는 사진을 100장 출력해보았더니 알맞게 나왔다.

# 픽셀별 평균값이 가까운 사진을 구하기
abs_diff = np.abs(fruits - apple_mean)
abs_mean = np.mean(abs_diff, axis=(1,2))
print(abs_mean.shape) # 300

apple_index = np.argsort(abs_mean)[:100]
fig, axs = plt.subplots(10, 10, figsize=(10, 10))
for i in range(10):
  for j in range(10):
    axs[i,j].imshow(fruits[apple_index[i*10 + j]], cmap = 'gray_r')
    axs[i, j].axis('off')

plt.show()

K-평균 알고리즘

k-평균 알고리즘은 비지도 학습에서 클러스터링(군집) 중 하나이다. 작동 방법은우선 k개의 클러스터를 지정한 다음에 각 샘플에서 가장 가까운 클러스터를 기준으로 그룹을 만들어주고, 그 샘플들의 평균값으로 클러스터의 지점을 변경해주고 다시 그 클러스터를 기준으로 그룹을 만들어주고를 반복한다. 언제까지? 클러스터 지점에 변경이 없을 때 까지(귀찮아서 내가 쓴 과제에서 가져옴).

from sklearn.cluster import KMeans

km = KMeans(n_clusters = 3, random_state = 42)
km.fit(fruits_2d)

print(km.labels_)

여기서 클러스터의 최적의 갯수를 구하기 위해서는 이너셔(클러스터 중심과 샘플간의 거리 제곱 합)을 이용하는데, k값을 변화해가며 이너셔를 구해서 이너셔 감소가 꺾이는 지점이 좋은 K값이다.

# 이너셔 값 구하기
inertia = []
for k in range(2, 7):
  km = KMeans(n_clusters = k, random_state = 42)
  km.fit(fruits_2d)
  inertia.append(km.inertia_)

plt.plot(range(2, 7), inertia)
plt.xlabel('k')
plt.ylabel('inertia')
plt.show()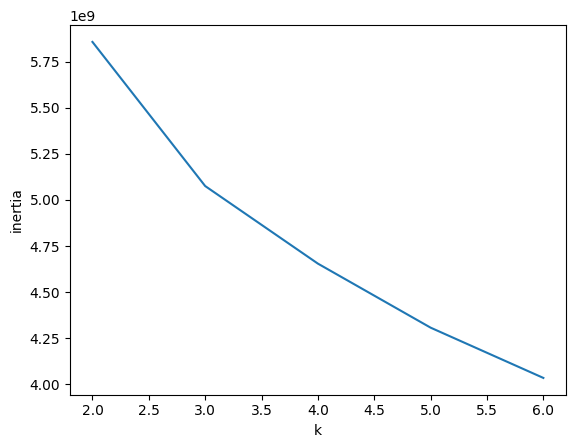

주성분 분석(차원 축소)

주성분 분석은 데이터의 차원을 축소하여 (특성의 개수를 줄여) 용량의 축소와 추후 프로세스에 걸리는 시간 축소, 과대적합 방지등의 역할을 할 수 있다. 주성분 분석은 데이터의 분산을 값으로 지정해 주성분 값으로 설정하여 진행한다. 코드는 PCA 모델을 먼저 생성한 후(n_components는 주성분의 개수이다) 데이터에 fit을 해준뒤 그 pca를 토대로 transform 까지 해주어야 데이터의 특성이 주성분의 값으로 변환된다.

# 주성분 분석
from sklearn.decomposition import PCA
pca = PCA(n_components = 50)
pca.fit(fruits_2d)
fruits_pca = pca.transform(fruits_2d)

과제

1. k-평균 알고리즘 작동 방식 설명하기
   A: 우선 k개의 클러스터를 지정한 다음에 각 샘플에서 가장 가까운 클러스터를 기준으로 그룹을 만들어주고, 그 샘플들의 평균값으로 클러스터의 지점을 변경해주고 다시 그 클러스터를 기준으로 그룹을 만들어주고를 반복한다. 언제까지? 클러스터 지점에 변경이 없을 때 까지

2. 6-3 확인 문제 풀고, 풀이 과정 정리하기
   Q-1 특성이 20개인 대량의 데이터셋이 있습니다. 이 데이터셋에서 찾을 수 있는 주성분 개수는 몇 개일까요?
   A-1 주성분 개수는 특성의 개수와 동일하게 찾을 수 있다. 답은 20개이다

Q-2 샘플 개수가 1000개이고 특성 개수는 100개인 데이터셋이 있습니다. 즉 이 데이터셋의 크기는 (1000, 100) 입니다. 이 데이터를 사이킷런의 PCA 클래스를 사용해 10개의 주성분을 찾아서 변환했습니다. 변환된 데이터셋의 크기는 얼마일까요?
A-2 2차원 부분이 특성 부분이고 100개의 특성을 10개의 주성분으로 변환하였으니 (1000, 10)이다.

Q-3 2번 문제에서 설명된 분산이 가장 큰 주성분은 몇번째인가요?
A-3 주성분 분석은 특성이 잘 설명되는 순서대로 주성분이 선택 되기 때문에 첫 번째 주성분이 가장 잘 설명한다고 볼 수 있다.