MIT 6.006 Introduction to Algorithms 1강을 보고 정리한 내용입니다.
링크: https://www.youtube.com/watch?v=ZA-tUyM_y7s&list=PLUl4u3cNGP63EdVPNLG3ToM6LaEUuStEY
알고리즘과 자료구조를 왜 배울까?
- computational problem을 잘 푼다. 어떻게?
- 정확하고
- 효율적이게
여기까진 식상하다고 생각할 수도 있다. 하지만 Jason Ku 교수님은 얼마나 정확하고 효율적이게 문제를 풀었는지 개발자들 간에 소통하기 위해 자료구조 및 알고리즘을 배워야한다고 하였다. 여태 문제 해결 능력의 중요성에 중점을 두고 있던 나는 소통 및 협업에 대한 열망을 가지게 되는 계기가 되었다.
Problem
문제를 잘 풀기 전에 일단 문제가 무엇인지 정의내려야 한다. 결론부터 말하자면 문제란 입력으로부터 정답인 출력을 알아내는 것이다. 여기서 입력의 크기는 작은 경우보다 큰 경우가 더 보편적이다. 따라서, 큰 입력 n에 대하여 효율적으로 알고리즘을 짜는 것이 중요하다.
Algorithm
알고리즘이란 앞서 말한 입력으로부터 정답을 출력하는 문제를 푸는 함수이다. 함수의 정의를 상기시켜 보자.
함수
두 변수 x, y에 대하여 x가 정해지면 그에 따라 y의 값이 오직 하나로 결정될 때, y를 x의 함수라고 한다.
따라서 방법이 어떻든 입력이 같다면 출력이 같아야 한다. 다시 강조하자면 문제에 대한 답을 얻어낼 수 있는 정확하고 다양한 방법 중 효율적인 방법을 찾아야 한다.
Correctness
그렇다면 사용한 알고리즘이 참임을 어떻게 밝힐지 알아보자. 입력이 작다면 케이스별로 분석하면 되지만 입력이 클 때는 모든 케이스를 직접 고려할 수 없다. 입력이 큰게 더 보편적이므로 중요한데 이때 사용하는 방법이 induction이다. Induction은 작은 값으로부터 큰 값으로 확장시켜나간다.
induction
- 상황 예시: 학생들 중 생일이 같은 경우 찾아내기
- 문제: induct on k
- 가정: 만일 k까지 match가 있다면, k+1번째 경우를 비교해보기전에 return한다
- Base case: k = 0 (k = 0이기 떄문에 match가 없을 것)
- k = k'에 대하여 match가 있다면 k = k'+1에 대하여 자연스레 match가 포함
- induction에 의해 return- k = k'에 대하여 match가 없고 k'+1에 대하여 match가 있다면 match가 k'+1을 포함
- 알고리즘은 이때 k'+1번째 학생의 생일과 앞의 k'번째 학생까지의 생일 중 같은 날짜가 있는지 확인
Efficiency
앞서 문제를 정확하게 푸는 방법에 대하여 논하였다. 이제 효율적으로 문제를 푼다는 것의 의미에 대하여 생각해보자. 가장 먼저 떠올릴 수 있는 방법이 문제 푸는 속도를 측정하는 것이다. 하지만 구글에서 사용하는 슈퍼컴퓨터와 노트북의 차이를 생각하면 이러한 방법이 절대적이지 않을 수 있다는 것을 곧 깨닫는다. 시간에 영향을 미치는 요소가 알고리즘의 효율성 뿐 아니라 하드웨어의 성능도 있기 때문이다. 따라서, 시간을 예측하는 것보다 operations(연산량)을 측정하는 것이 적합하다. 연산량은 입력의 크기 n에 종속적인데 입력의 크기는 큰 것이 더 보편적이므로 큰 n에 대하여 연산량이 적은 알고리즘이 효율적이다.
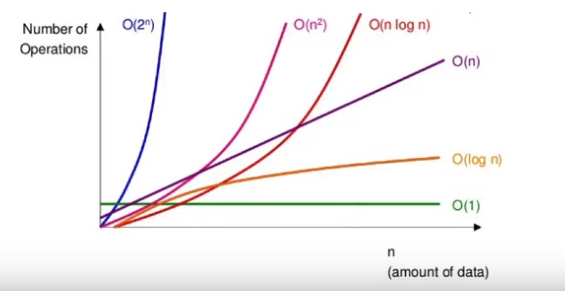
입력의 크기에 따라 연산량의 크기를 표시할 수 있는 방법이 유명한 빅오 표기법이다. 빅오는 Upper bound인데 lower bound tight bound라는 개념도 있다는 것을 알아두자.

Model of Computation
Efficiency에서 빅오에 대하여 배웠는데 입력에 대하여 독립적인 O(1)은 어떠한 operation에 해당하는지 생각해보자. 그 전에 몇 가지 용어를 정리한다.
- Word-RAM
- bit: 0과 1
- Machine word: 연속적인 bit의 뭉텅이
- RAM: Random access memory로 임의의 주소로 접근 가능한 machine word
- w-bit Word-RAM: CPU가 메모리로부터 한 순간에 받아들이고 연산할 수 있는 크기를 의미한다. w word 크기의 Word-RAM으로 크기를 가지며
참고로 32bit 컴퓨터는 ≈ 4GB, 64bit 컴퓨터는 ≈ 20EB의 메모리 연산이 가능하다.
다시 위의 질문으로 돌아가면,2개의 machine word에 대하여 binary 연산에 대하여 O(1) operation에 해당하는 것들은 다음과 같다.
- integer arithmetic: +, -, *, //, %
- logical operator: &&, ||, !, ==, <, >, <=, =>
- bitwise arithmetic: &, |. <<, >>, ...
- word a에 대하여 a의 메모리 주소에 읽기, 쓰기
Data Structure
data structure이란 가변적인 크기의 데이터를 저장해서 그 데이터를 가지고 operation들을 할 수 있도록한다. 여기서 하는 operation들이 interface에 해당한다. 하나의 interface에 대하여 여러가지 data structure를 사용할 수 있다. 따라서 각 interface에 가장 효율적인 data structure를 찾는 것이 중요하다. 하나의 예시로 앞서 induction에서 상황 예시를 들었던 같은 생일 찾기 문제를 static array라는interface로 풀어보자.
- StaticArray (n): 모두 0으로 초기화된 크기가 n인 새로운 static array를 지정
- 연산량: O(n)
- StaticArray.get_at(i): index i에 저장되어 있는 단어를 반환
- 연산량: O(1)
- StaticArray.set_at(i, x): index i에 word x를 write
- 연산량: O(1)
참고로 python에서 tuple은 set_at(i, x) 기능(수정 기능)이 없는 static array와 같고 list는 dynamic array를 도입한다.
class StaticArray:
def __init__(self, n):
self.data = [None] * n
def get_at(self, i):
if not (0 <= i < len(self.data): raise IndexError
return self.data[i]
def set_at(self, i, x):
if not (0 <= i < len(self.data): raise IndexError
self.data[i] = x
def birthday_match(students):
'''
Find a pair of students with the same birthday
Input: tuple of student (name, bday) tuples
Output: tuple of student names or None
'''
n = len(students) # O(1)
record = StaticArray(n) # O(n)
for k in range(n): # n
(name1, bday1) = students[k] # O(1)
for i in range(k): # k Check if in record
(name2, bday2) = record.get_at(i) # O(1)
if bday1 == bday2: # O(1)
return (name1, name2) # O(1)
record.set_at(k, (name1, bday1)) # O(1)
return None # O(1)
How to Solve an Algorithms Problem
문제를 효율적으로 정확하게 푼다는 것의 정의가 1강의 핵심이다. 그렇다면 6.006에서 앞으로 다룰 문제들을 크게 분류해본다.
- Data structure & sorting
- Shortest path algorithms & graphs
- dynamic programming
