MIT 6.006 Introduction to Algorithms 2강을 보고 정리한 내용입니다.
링크: https://www.youtube.com/watch?v=CHhwJjR0mZA&list=PLUl4u3cNGP63EdVPNLG3ToM6LaEUuStEY&index=2
Interface vs Data Structures
1강의 주제는 문제를 정확하고 효율적이게 푸는 것이었다. 2강은 문제를 풀기 위한 interface와 data structure에 대한 정의로 시작한다. 문제가 주어졌을 때 무엇을 하고 싶은지 문제를 구체화시키는 과정이 interface이며 구체화된 문제를 어떻게 해결할지를 나타내는 과정이 data structure이다. 컴퓨터로 문제를 푼다는 것은 결국 데이터를 저장하여 저장된 데이터를 연산하는 과정이다. 데이터 관점에서 보았을 때 interface란 1. 어떤 종류의 데이터를 저장할지 2. 어떤 operation이 가능한지와 그것이 의미하는 바가 무엇이지를 구체화하는 문제 정의 과정이다. Data structure란 1. 데이터를 저장하는 방법이며 2. operation들을 수행할 알고리즘을 통해 문제를 해결하는 방법이다.
Interface와 datastructure에 대한 정의가 추상적이어서 한번에 와닿지 않을 수 있다. 따라서
데이터에 대한
- interface: 문제 정의
- data structure: 문제 해결
라는 큰 틀 속에서 구체적인 예시를 통해 이해해볼 수 있도록 강의가 구성되어있다.
2강에서 다룰
interface와data structure
- interface: sequence
- data structure: array, pointer based(linked list)
interface: sequence
Sequence는 extrinsic한 순서로 collection of items의 순서가 유지된다. 예를 들어 첫 번째 item이 첫 번째인 이유는 그 item이 무엇인지가 중요한 것이 아니라 외부에서 첫번째 순서에 그 item을 배치했기 때문이다. 따라서 어떤 item을 찾기 위해서는 sequence의 rank를 통해 찾는다.
data structure: array
컴퓨터 메모리는 한정적인 자원이다. OS(operating system)는 각 process마다 고정된 뭉텅이의 메모리의 주소들을 할당한다. 할당하는 메모리의 크기는 process의 요구사항과 사용 가능한 메모리 여유에 따라 달라진다. 예를 들어 컴퓨터 프로그램은 OS에 어떠한 변수를 저장할지와 더불어 얼만큼의 메모리(bit)가 필요한지 지정한다. 이러한 요구를 맞추기 위해 OS는 필요한 메모리의 크기만큼 메모리 속에 비어있는 공간을 찾아 데이터를 저장한다. 메모리 관리와 할당이 파이썬과 같은 high-level 언어에서는 생략되어 있어서 생소한 개념일 수 있지만 뒤에서 이러한 과정들을 파이썬이 처리해주고 있다.
컴퓨터 프로그램이 10 64-bit words (640 bit)크기의 2개의 array를 저장하고 싶은 상황을 가정해보자. 이때, 1280bit가 연속적으로 비어있는 공간을 찾았다고 추가적인 가정을 해본다. 이 상황에 첫 번째 array A를 비어있는 주소 공간에 저장하고 두 번째 array B를 바로 오른쪽에 저장하였다. 이때 만약 A에 11번째 word 를 추가하고 싶다면 어떻게해야 할까? A의 오른쪽에 있는 B를 shift시켜 A를 위한 공간을 확보해주는 방법을 가장 먼저 떠올려본다. 하지만 이런 방법은 B의 오른쪽에도 메모리가 차있을 경우를 고려하지 않은 방법이다. B의 오른쪽 공간에 엄청나게 많은 데이터가 저장되어 있다면 그 데이터들도 함께 옮겨주어야할까? 그러한 방법은 얼핏봐도 매우 비효율적이다. 이보다 더 나은 방법은 11 64-bit words (704bit)크기의 새로운 메모리 공간을 찾아 array A에 있는 정보들을 복사한 후 11번째 word 를 추가해주는 방법이다.
P1. interface: static sequence
Sequence interface의 가장 기본적인 형태는 static sequence interface이다. Static sequence interface는 item의 개수가 변하지 않는 특징이 있고, item 자체는 바뀔 수 있다. 앞서 interface를 어떠한 operation들이 가능한지 구체화하는 문제 정의 과정이라고 하였다. 따라서, 순서의 item을 유지할 수 있는 operation들을 확인해보자.
| 종류 | operation | 설명 |
|---|---|---|
| container | build(X) | iterable X가 주어졌을 때 X의 item들로 sequence를 만듦 |
| len() | 저장되어 있는 item의 수 을 반환 | |
| static | iter_seq() | 저장되어 있는 를 sequence 순서에 따라 하나씩 반환 |
| get_at(i) | 번째 item 을 반환 | |
| set_at(i, x) | 번째 item을 로 바꿈 | |
| get_first/last(i) | special case에 대해 더 효율적으로 구현할 수도 있기 때문에 따로 생각 | |
| set_first/last(i,x) | special case에 대해 더 효율적으로 구현할 수도 있기 때문에 따로 생각 |
P1-S1. data structure: static array
Static sequence의 operation들의 연산을 가장 효율적으로 수행할 수 있도록 하는 data structure는 static array다. 가장 효율적인 이유는 seqeuence는 특정한 순서로 item들을 저장되어 있어서 순서(index)에 따라 item에 접근하는데 static array는 연속적인 메모리 공간에 item들을 저장하기 때문이다.
Static array는 처럼 index 를 통해 바로 원소에 접근 가능하기 때문에, 다시 말해서 이기 때문에, 는 시간이 걸린다. 또한 static array는 크기도 바로 알 수 있으므로 시간이 걸린다. 하지만 array를 새로 만들거나 하나씩 반환해야 한다면, 모든 원소를 처리해야 하므로 시간이 걸린다.
| 종류 | operation | |
|---|---|---|
| container | build(x) | |
| len() | ||
| static | iter_seq() | |
| get_at(i) | ||
| set_at(i,x) |
class Array_Seq:
def __init__(self): # O(1)
self.A = []
self.size = 0
def __len__(self): # O(1)
return self.size
def __iter__(self): # O(n)
yield from self.A
def build(self, X): # O(n)
self.A = [a or a in X]
self.size = len(self.A)
def get_at(self, i): # O(1)
return self.A[i]
def set_at(self, i, x): # O(1)
self.A[i] = xMemory allocation model
크기가 인 static array를 만드는 과정은 결국 메모리 공간의 크기를 어떻게 지정해주느냐가 관건이다. 가 시간이 걸리도록 하기 위해선 데이터를 연속적으로 저장해야 하기 때문이다. 따라서, 충분한 메모리 공간을 필요로 한다. 크기가 인 문제를 저장하기 위해 최소 의 공간이 필요하므로 다음과 같은 가정이 선행된다.
n: problem size w: machine word size
P2. interface: dynamic sequence
Dynamic sequence는 기본적으로 static sequence에서 구현되었던 operation들을 기본으로 item을 삽입 및 수정과 같은 dynamic한 operation들이 추가적으로 가능한 interface다.
dynamic sequence operations = static sequence operations + dynamic operations
| 종류 | operation | 설명 |
|---|---|---|
| container | build(X) | iterable X가 주어졌을 때 X의 item들로 sequence를 만듦 |
| len() | 저장되어 있는 item의 수 을 반환 | |
| static | iter_seq() | 저장되어 있는 를 sequence 순서에 따라 하나씩 반환 |
| get_at(i) | 번째 item 을 반환 | |
| set_at(i, x) | 번째 item을 로 바꿈 | |
| get_first/last(i) | special case에 대해 더 효율적으로 구현할 수도 있기 때문에 따로 생각 | |
| set_first/last(i,x) | special case에 대해 더 효율적으로 구현할 수도 있기 때문에 따로 생각 | |
| dynamic | insert_at(i,x) | 를 새로운 로 지정하고 기존의 는 , 는 , ... 와 같이 부터 까지의 원소를 모두 이동 |
| delete_at(i) | 원소를 삭제한 후 는 , 는 , ... 와 같이 부터 까지의 원소를 모두 이동 | |
| insert_first(x) | special case에 대해 더 효율적으로 구현할 수도 있기 때문에 따로 생각 | |
| delete_first(x) | special case에 대해 더 효율적으로 구현할 수도 있기 때문에 따로 생각 | |
| insert_last(x) | special case에 대해 더 효율적으로 구현할 수도 있기 때문에 따로 생각 | |
| delete_last() | special case에 대해 더 효율적으로 구현할 수도 있기 때문에 따로 생각 |
P2-S1. data structure: static array
앞서 첫번째 interface인 static sequence를 구현하기 위한 data structure로 static array가 직관적으로 가장 효율적이었음을 확인하였다. Dynamic sequence와 같이 삽입/삭제와 같은 dynamic operation들에도 static array가 가장 효율적인 data structure일까? Static array는 item의 개수가 변하지 않도록 정하였으므로 dynamic operation이 일어날 때마다 새로운 메모리 공간으로 데이터를 복사해서 옮겨줘야하기 때문에 시간이 소요된다.
| 종류 | operation | |
|---|---|---|
| container | build(x) | |
| len() | ||
| static | iter_seq() | |
| get_at(i) | ||
| set_at(i,x) | ||
| dynamic | insert_at(i,x) | |
| delete_at(i) |
class Array_Seq:
# static array operations
def __init__(self): # O(1)
self.A = []
self.size = 0
def __len__(self): # O(1)
return self.size
def __iter__(self): # O(n)
yield from self.A
def build(self, X): # O(n)
self.A = [a or a in X]
self.size = len(self.A)
def get_at(self, i): # O(1)
return self.A[i]
def set_at(self, i, x): # O(1)
self.A[i] = x
# dynamic operations
def _copy_forward(self, i, n, A, j): # O(n)
for k in range(n):
A[i+j] = self.A[i+k]
def _copy_backward(self, i, n, A, j): # O(n)
for k in range(n-1, -1, -1):
A[j+k] = self.A[i+k]
def insert_at(self, i, x): # O(n)
n = len(self)
A = [None] * (n + 1)
self._copy_forward(0, i, A, 0)
A[i] = x
self._copy_forward(i, n-i, A, i+1)
self.build(A)
def delete_at(self, i): # O(n)
n = len(self)
A = [None] * (n - 1)
self._copy_forward(0, i, A, 0)
x = self.A[i]
self._copy_forward(i + 1, n - i - 1, A, i)
self.build(A)
return x
# O(n)
def insert_first(self, x):
self.insert_at(0, x)
def delete_first(self):
return self.delete_at(0)
def insert_last(self, x):
self.insert_at(len(self), x)
def delete_last(self):
return self.delete_at(len(self) - 1)
Static sequence의 경우 static array를 도입했을 때 처음 sequence를 만드는 나 sequence 내의 값들을 반환하는 와 같은 특수한 경우를 제외하고는 시간이 소요되어 효율적이었다. 그에 반해 dynamic sequence의 경우 추가/삭제 작업이 주된 operation인데 static array 도입 시 시간이 소요되므로 최선의 자료구조가아님을 확인하였다.
P2-S2. data structure: linked list
앞서 static array는 static operation들을 수행하는 데에 있어서 대부분 시간이 걸려 효율적이나, dynamic operation들을 수행할 때는 시간이 걸려 비효율적인 것을 확인하였다. dynamic operation들을 아래의 두가지 동작으로 인해 비효율적이다.
- array를 다른 곳에 배치
- 바뀐 item에 따라 shifting 연산 수행(?)
사실 엄밀히 말하자면 array의 길이가 바뀔 때마다 모든 원소를 메모리상의 다른 위치로 이동하기 때문에 2번의 shifting은 static array에서 불필요한 작업이다. 1번이 이루어지지 않는다는 가상의 상황에 2번을 고려해보자.이 경우 item들이 삽입/삭제한 item의 개수만큼 shifting해줘야 한다.
Dynamic operation을 효율적으로 수행하기 위해선 삽입/삭제를 해야할 때마다 모든 item을 메모리의 다른 위치에 재배치 및 shifting하지 않아야 한다. 이러한 문제를 해결해주는 자료구조가 linked list 자료구조다.
Static array가 dynamic operation을 효과적으로 수행할 수 없었던 원인은 item들이 연속적인 메모리 공간에 할당되었기 때문이다. 그렇다면 item들을 임의의 빈 메모리 공간에 흩어지도록 할당한다면 문제가 해결된다. Array sequence에서 원소를 삽입/삭제하더라도 변화된 크기의 새로운 메모리 공간으로 옮길 필요가 없기 때문이다. 하지만 메모리가 흩어져있다면 sequence의 원소들을 더 이상 메모리상 위치한 순서로 찾을 수 없게 된다. 그렇다면 메모리상 다음 원소가 어디에 저장되어 있는지 메모리 주소를 원소의 값과 함께 저장해준다면 문제가 해결되지 않을까? 이러한 생각에서 출발한 자료구조가 linked list다.
Linked list는 각 원소를 node라는 단위에 저장한다. 노드는 앞서 말한 것처럼 원소값과 다음 노드의 주소를 저장해야한다. 따라서 원소값을 node.item에 저장하고, 다음 노드의 주소를 node.next에 저장한다.
class Linked_list_Node:
def __init__(self, x): # O(1)
self.item = x
self.next = None
def later_node(self, i): # O(1)
if i == 0:
return self
assert self.next
return self.next.later_node(i-1)Linked list는 pointer-based라고도 부르는데 메모리상 어느 위치에도 저장될 수 있기 때문에 유연하다는 장점이 있다. 따라서 삽입/삭제할 때도 해당 노드를 삽입/삭제한 후 직전 노드의 주소를 바꿔주면 되기 때문에 시간이 소요된다. 여태 dynamic operation들에만 집중을 했었는데 다시 돌아와서 static operation을 생각해보자. Static array의 경우 연산을 수행하기 위해 item을 찾을 때 와 같이 찾았었다. 그에 반해 linked list의 노드는 다음 원소의 주소만 저장되어있기 때문에 원하는 순서의 노드를 찾기 위해선 해당 원소가 나올 때까지 모든 원소를 시작노드인 head부터 거쳐가야 한다. 이 과정에서 소요되는 시간은 시간이다. 따라서, 노드를 삽입/삭제하는 연산 자체는 시간이 걸리지만 임의의 원소를 삽입/삭제하기 위해선 그 원소를 찾을때까지 시간이 걸린다. 그렇기 때문에 linked list의 첫번째 요소를 삽입/삭제하는 를 제외한 에 시간이 아닌 시간이 소요된다.
| 종류 | operation | |
|---|---|---|
| container | build(x) | |
| len() | ||
| static | iter_seq() | |
| get_at(i) | ||
| set_at(i,x) | ||
| dynamic | insert_at(i,x) | |
| delete_at(i) | ||
| insert_first(i,x) | ||
| delete_first(i) |
class Linked_List_Seq:
def __init__(self): # O(1)
self.head = None
self.size = 0
def __len__(self): # O(1)
return self.size
def __iter__(self): # O(n) iter_seq
node = self.head
while node:
yield node.item
node = node.next
def build(self, X): # O(n)
for a in reversed(X):
self.insert_first(a)
def get_at(self, i): # O(i)
node = self.head.later_node(i)
return node.item
def set_at(self, i, x): # O(i)
node = self.head.later_node(i)
node.item = x
def insert_first(self, x): # O(1)
new_node = Linked_List_Node(x)
new_node.next = self.head
self.head = new_node
self.size += 1
def delete_first(self): # O(1)
x = self.head.item
self.head = self.head.next
self.size -= 1
return x
def insert_at(self, i, x): # O(i)
if i == 0:
self.insert_first(x)
return
new_node = Linked_List_Node(x)
node = self.head.later_node(i - 1)
new_node.next = node.next
node.next = new_node
self.size += 1
def delete_at(self, i): # O(i)
if i == 0:
return self.delete_first()
node = self.head.later_node(i-1)
x = node.next.item
node.next = node.next.next
self.size -= 1
return x
# O(n)
def insert_last(self, x):
self.insert_at(len(self), x)
def delete_last(self):
return self.delete_at(len(self) - 1)요약하자면 와 같은 dynamic한 operation들의 시간복잡도를 낮추려 linked list 자료구조를 생각해냈으나, 그 중 특수한 경우인 를 제외한 dynamic operation의 시간은 으로 변함이 없었으며, 심지어 static한 operation인 의 경우 static array를 도입했을 때 시간이 소요된 것에 반해 시간이 소요되었다. 결국, dynamic sequence interface에 linked list도 효과적인 자료구조가 아님을 확인하였다.
P2-S3. data structure: dynamic array
Linked list는 에 static array에서 시간이 걸리는 것에 반해 시간이 걸리지만 static array가 에 시간이 걸리는 것과 비교되게 시간이 걸린다. 다시 말해서, static array는 연산을 제외하곤 linked list보다 시간복잡도에 있어서 우위에 있다. 그렇다면 static array에 변화를 주어 는 아니지만 에 있어서 시간이 소요되도록 하는 자료구조가 dynamic array다.
앞서 P2-S2.data structure: linked list에서 static array에서의 dynamic operation이 오래 걸리는 이유가 아래 두가지였다.
- array를 다른 곳에 배치
- 바뀐 item에 따라 shifting 연산 수행(?)
2번의 경우 static array의 특성 연속적인 메모리 공간에 item들을 저장한다는 특성으로 인해 바꿀 수 없다. 그렇기 때문에 의 시간복잡도를 으로 줄일 수 없는 것이다.
Array는 길이가 변하지 않도록 설정했기 때문에 1번과 같이 동작하는데, 길이가 변할 수 있도록 한다면 1번은 해결 가능한 문제다. 그럼 애초에 왜 array는 길이를 변하지 않도록 설정했을까? 임의의 비어있는 메모리 공간에 원소들을 할당하였기 때문에 그 공간 오른쪽도 메모리 공간이 비어있다는 것을 보장할 수 없기 때문이다. 여기서 나올 수 있는 해결책은 sequence interface의 크기보다 큰 메모리 공간을 할당해서 여유 공간을 남기는 것이다. 이러한 자료구조가 dynamic array다. 엄밀히 말하자면 dynamic array도 array이기 때문에 길이가 변하지 않지만, 필요할 때만 1.array를 다른 곳에 배치하는 과정을 충분히 다이나믹(유연)하다고 생각해서 이렇게 이름을 지은 것 같다.
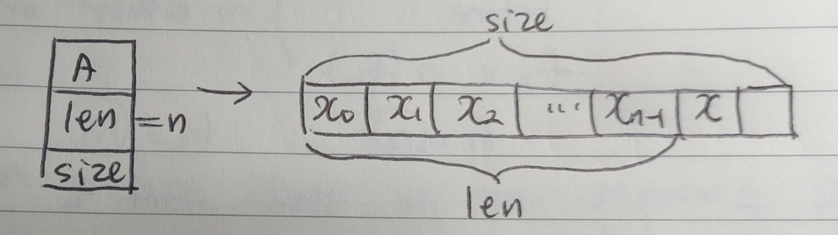
위 그림과 같은 경우 마지막에 원소를 하나 추가하거나 삭제하더라도 모든 원소를 메모리상 다른 위치로 배치할 필요가 없다. 물론 array 중간에 item들을 삽입/삭제한다면 2번의 shifting 작업이 필요하다. 따라서 에 있어서 시간이 소요되는 반면에 는 시간이 소요된다. 위 그림에서 만약에 원소를 두 번째로추가하더라도 에 시간이 소요될까? 아니다. 시간이 걸린다. 할당된 메모리 공간보다 sequence의 길이가 더 길어지기 때문에 1.array를 다른 곳에 배치하는 작업이 요구되기 때문이다.
그렇다면 할당하는 메모리 공간을 무한대로 늘린다면 1번 작업이 필요없지 않겠는가? 맞다. 하지만 그렇게된다면 유한한 자원인 메모리 공간을 낭비하는 셈이다. 따라서 절충안이 필요하다. 아주 가끔씩만 메모리 공간을 재할당하도록하여 시간이 걸리지만, 대부분의 경우 차지하는 메모리 공간을 유지하도록 하여 시간이 걸리도록 한다. 이렇게되면 에 평균적으로 의 시간이 소요된다. Sequence operation들의 평균을 내는 과정을 amortization이라고 한다.
다시 돌아가서, 메모리 공간을 재할당하는 과정이 시간이 걸린다고 했는데 증명해보자. 재할당하는 메모리 공간은 기존의 메모리 공간 * r(ratio)로 정한다. 만일 메모리 공간 할당하는 작업을 수행할 때 새로운 공간의 크기를 기존의 2배로 설정한다면, resize cost가 임을 수식으로 증명해보자.
resize cost
=
=
=
=
| 종류 | operation | |
|---|---|---|
| container | build(x) | |
| len() | ||
| static | iter_seq() | |
| get_at(i) | ||
| set_at(i,x) | ||
| dynamic | insert_at(i,x) | |
| delete_at(i) | ||
| insert_first(i,x) | ||
| delete_first(i) | ||
| insert_last(i,x) | ||
| delete_last(i) |
class Dynamic_Array_Seq(Array_Seq):
def __init__(self, r = 2): # O(1)
super().__init__()
self.size = 0
self.r = r
self._compute_bounds()
self._resize(0)
def __len__(self): # O(1)
return self.size
def __iter__(self): # O(n)
for i in range(len(self)):
yield self.A[i]
def build(self, X): # O(n)
for i in X:
self.insert_last(a)
def _compute_bounds(self): # O(1)
self.upper = len(self.A)
self.lower = len(self.A) // (self.r * self.r)
def _resize(self, n): # O(1) or O(n)
if (self.lower < n < self.upper):
return
m = max(n, 1) * self.r
A = [None] * m
self._copy_forward(0, self.size, A, 0)
self.A = A
self._compute_bounds()
def insert_last(self, x): # O(1) a
self._resize(self.resize + 1)
self.A[self.size] = x
self.size += 1
def delete_last(self): # O(1) a
self.A[self.size - 1] = None
self.size -= 1
self._resize(self.size)
def insert_at(self, i, x): # O(n)
self.insert_last(None)
self._copy_backward(i, self.size - (i + 1), self.A, i)
self.A[i] = x
def delete_at(self, i): # O(n)
x = self.A[i]
self._copy_forward(i + 1, self.size - (i + 1), self.A, i)
self.delete_last()
return x
# O(n)
def insert_first(self, x):
self.insert_at(0, x)
def delete_firtst(self):
return self.delete_at(0)보통 sequence interface 중에서 삽입/삭제와 같은 dynamic한 operation이 있는 dynamic sequence가 보편적인데 dynamic sequence의 operation들을 가장 잘 구현하는 자료구조가 dynamic array임을 확인하였다. 파이썬의 list가 내부적으로 dynamic array를 구현하였다고 한다. 위의 함수들은 파이썬의 list가 구현한 동작들을 간략하게 보여준다. 파이썬이 내가 배운 첫 번째 언어였기에 큰 생각을 하지 않고 여태 사용해왔었는데 dynamic array 연산들을 가장 효율적으로 연산하는 자료구조인 dynamic array를 도입하고 있었다고 생각하니 파이썬의 위대함을 다시 한번 느꼈다. 또한 알고리즘 문제를 풀 때 list를 막연하게 사용해오고 있었는데 왜 list가 좋은 선택인지에 대해 깨닫게되는 계기였다.
