스탠포드 강의의 CS231 7강을 보고 정리한 내용입니다.

링크 : https://www.youtube.com/watch?v=_JB0AO7QxSA&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk&index=7

[Optimization]
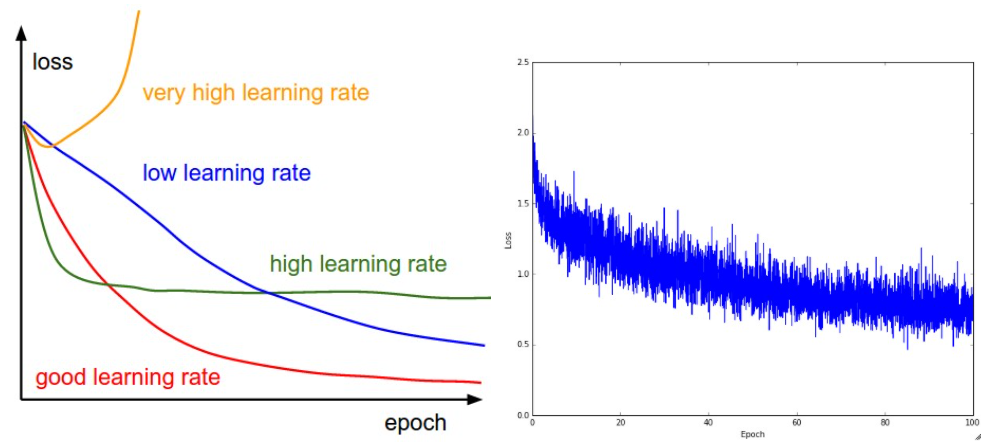
6강에서 loss function 그래프를 보면서 hyperparameter인 learning rate를 조절하는 방법에 대해 다뤘다. 여기서 말하는 learning rate는 optimization시 한 번 움직일 때의 폭이다. 따라서 너무 크게도 작게도 아닌 적당한 수준으로 정하는 작업이 필요했다. Hyperparameter tuning 방법으로 learning rate를 조절해서 모델의 성능을 미세하게 높이는 것도 중요하지만 보다 근본적으로 optimization 자체를 바꿔보는 방법도 생각해볼 수 있다. 우리가 여태 접한 optimization 방법은 3강에서 배운 stochastic gradient descent뿐이다. SGD는 minibatch를 이용하기 때문에 stochastic한 특성으로 인해 아래 그림에서 볼 수 있듯이 loss 값이 너무 많이 흔들린다. 또한 매순간 가장 큰 gradient 값의 반대 방향으로 이동하기 때문에 gradient가 0인 지점에서는 학습을 멈추게 된다. 이번 시간에는 SGD의 단점을 보완해줄 optimizer들에 대해 알아보겠다.

[Regularization]
5강에서는 최대한 적은 parameter로 깊게 쌓아준다는 관점으로 convolutional neural network를 이해했다. 큰 모델을 학습할 때 얼핏하면 overfitting이 발생해서 해결하기 위해 다양한 regularization 방법들을 쓴다. 그렇다면 애초에 왜 작은 모델을 쓰지 않고 모델을 깊게 쌓아 큰 모델을 만든 후 overfitting을 방지하기 위한 여러가지 방법을 쓸까? 즉, 왜 모델을 복잡하게 설계하는지에 대해 먼저 이해하고 넘어가야 regularization을 배우는 의미를 깨닫게 된다.

[Transfer learning]
모델을 깊고 크게 쌓아주게 되면 근원적으로는 모델의 크기에 비해 데이터의 수가 부족하게 된다. 데이터의 수가 모델의 크기에 비해 적기 때문에 모델이 training 데이터를 암기해버리는 경우가 생기는데 이런 현상을 overfitting이라고 한다. Overfitting을 해결하기 위해 가장 직관적으로 떠올릴 수 있는 방법은 데이터를 다 암기했으니까 training 데이터의 수를 늘려서 암기 못하게 해버리는 것이다. 하지만 현실적으로 데이터를 늘리는 것은 데이터 수집 과정의 어려움과 라벨링 작업 등의 이유로 비싸고 개인정보 보호 차원에서도 불가능한 경우가 다반사다. 이 때 갖고 있는 데이터의 변형(data augmentation)을 통해 데이터의 수를 늘릴 수 있다. 혹은, 데이터를 늘리지 않더라도 한 모델 안에서 다양한 기법들을 적용할 수 있다. 대표적으로 loss 식의 변형인 l1, l2 regularization, dropout, batch normalization가 있다. 추가적으로 여러 모델을 사용하는 방법도 있을 것이다.

이제 생각을 전환해보자. 데이터를 늘려준다거나 각종 regularization 기법들을 사용하는 대신에 그냥 적은 데이터로 학습할 순 없을까? 더 정확히 말하자면 데이터의 특성이 비슷할 때 ImageNet과 같이 큰 데이터셋에서 학습을 마친 모델과 그 weight 값들 가져와서 적은 데이터에 적용할 순 없을까? 이 아이디어가 바로 transfer learning이다.

1. Optimization

1.1 SGD

1.1-1 SGD 방법

3강에서 Stochastic gradient descent에 대해 배웠었다. Image classfication task에서 모델을 학습한다는 것은 최적의 weight 값을 찾아 분류를 잘하는 것이다. 최적의 weight 값을 찾기 위해 loss라는 성능 지표를 설정하고 loss를 줄이기 위해 기울기가 가장 큰 지점에서 음의 방향으로 이동하는게 gradient descent였다. 그 중 true gradient가 아닌 batch별로 noisy estimate of the gradient를 구하는 것이 stochastic gradient descent이다. 구체적인 과정은 아래 슬라이드에 나와있다.

1.1-2 SGD의 한계

Optimization은 가장 적은 training loss값을 가지는 W를 구하는 과정이다. SGD는 가장 먼저 직관적으로 떠올린 optimization 방법이었는데 크게 2가지 측면에서 단점이 있다.

SGD의 단점
1. Zigzagging behavior > 느린 학습 속도
2. 학습 종료

Zigzagging behavior

우선, 하나의 축에서는 완만하나 다른 축에서는 가파른 2차원 곡면을 가정해보자. 이 경우 완만한 방향에서의 loss는 너무 천천히 움직이고 가파른 방향에서의 loss는 너무 빨리 움직인다. 다시 말해서 gradient의 방향과 가장 작은 minima 방향이 일치하지 않게 된다. 그 결과 학습이 느려지게 되고 차원의 수가 높아질수록 min 방향과 max 방향의 크기 차이가 커지게 되므로 문제가 심각해진다.

학습 종료

Gradient descent는 가장 큰 기울기의 방향으로 이동하기 때문에 기울기가 0이되면 더 이상 이동할 수 없게 되어 학습이 종료된다. 기울기가 0이되는 경우는 크게 local minima와 saddle point로 나뉜다.

Local minima에서는 어느 방향으로 가더라도 loss 값이 커진다. 그에 반해 saddle point는 어느 방향으로 가면 loss 값이 커지고 다른 방향으로는 loss 값이 작아진다. 확률적으로 loss 값이 모든 방향에 대해 증가하는 것보다 어떤 방향으로는 증가, 어떤 방향으로는 감소하는 경우가 흔하다. 따라서 차원이 많아질수록 saddle point가 흔해질 것이므로 neural network에선 saddle point가 더 심각한 문제다.

1.2 momentum

SGD는 zigzagging으로 인한 느린 학습 속도가 느리다는 점, gradient가 0이 되는 지점에서 학습을 멈추게 되는 단점이 있다. 이러한 문제들은 gradient만이 아닌 추가적인 어떤 힘을 합해서 이동을 하게되면 해결할 수 있게 된다. 물리 시간에 배웠던 관성의 법칙을 떠올려보자.

• 관성(慣性)은 물체에 작용하는 힘의 총합이 0일 때, 운동의 상태를 유지하려는 경향을 말하며, 운동의 상태가 변할 때 물체의 저항력이다.

관성의 개념을 SGD에 도입해서 loss 곡면에서의 이동 방향을 수정하도록 한다. 수정 방법은 구체적으로 기존의 gradient 벡터에 관성력을 표현하는 새로운 벡터인 velocity의 벡터를 합해서 새로운 이동 방향을 구하는 것이다. 이러한 개념을 도입한 대표적인 Optimizer들로 SGD /w momentum과 Nesterov momentum이 있다. 다만, SGD /w momentum과 nesterov momentum의 차이는 gradient벡터와 velocity벡터를 더하는 방식에 있다.

1.2-1 : SGD with momentum

앞서 SGD의 단점을 보완해주기 위해 관성의 개념을 도입하였다. 관성의 법칙에 의하면 움직이는 물체는 외부적인 힘이 가해지지 않으면 그 속도를 유지한다. 여기서 핵심은 현재 진행하는 속도를 고려해야한다는 것이다. 여기서 말하는 진행하는 속도란 전 gradient들의 가중합이다.

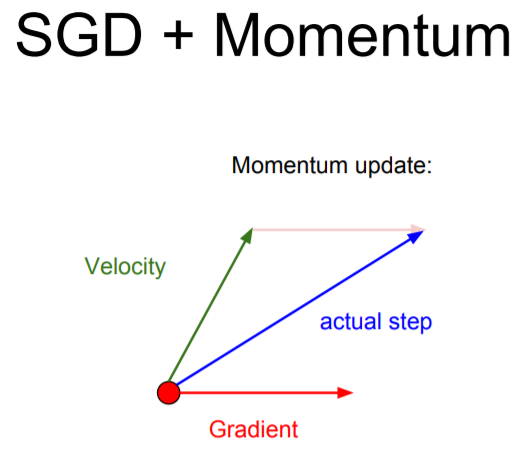
SGD /w momentum에서 실제 이동 방향은 기존의 gradient 벡터와 마찰계수를 곱한 velocity 벡터의 합 방향이다. 즉, 현재 위치에서의 gradient와 마찰계수를 통해 조금은 줄어든 현재의 속도를 동시에 고려하였다.

기존 SGD식과 비교해보면 SGD+Momentum이 관성력을 어떻게 도입했는지를 더 수월하게 이해할 수 있다.

• SGD
  다음 위치 X(t+1)는 현재 위치 X(t)에서 가장 큰 gradient 벡터로 learning rate라는 보폭을 통해 이동한 지점이다.
• SGD+Momentum
  다음 위치 X(t+1)는 현재 위치 X(t)에서 V(t+1)벡터로 learning rate라는 보폭을 통해 이동한 지점이다. 여기서 V(t+1)은 현재 속도에 ρ라는 마찰계수를 곱한 속도 벡터에 gradient 벡터를 더해준 벡터다. 여기서 속도와 gradient 벡터를 단순합하지 않고 ρ를 곱해준 이유는 관성의 법칙을 떠올리면 쉽게 이해할 수 있다. 현재의 속도에 어떠한 마찰도 주지 않은 상태에서 gradient 값만 계속 더해주게 된다면 갈수록 속도가 빨라지기 때문이다. 따라서 이런 상황을 방지하기 위해 현재의 속도를 감안하되 0.9나 0.99와 같이 현재의 속도를 조금은 줄여서 고려하도록 한다.

  SGD 단점 해결
  1.Zigzagging behavior으로 인한 느린 학습 속도
  : 현재의 속도를 더해줌으로써 빨라짐
  2.학습 종료
  : Saddle point나 local minima 지점에서 gradient=0이 되더라도 현재속도를 통해 그 지점에서 벗어남

하지만 gradient 벡터에 현재의 속도 벡터를 더해주기 때문에 새로운 문제가 발생하기도 한다. 현재의 속도 벡터는 전 gradient들의 가중합이기 때문에 gradient가 커지면 속도가 너무 빨라지게 된다. 이렇게 되면 마찰계수 ρ를 곱해주더라도 속도가 너무 빨라져 local minima를 지나치는 overshooting이 발생한다.

방금까지 local minima를 벗어날 수 있게되어서 SGD /w momentum이 효과적이라고 했는데 local minima를 벗어나게 되어서 overshooting되어 문제가 발생한다는 것은 얼핏보면 모순같다. Local minima의 특성에 따라 벗어나고 싶은지 수렴하고 싶은지가 결정된다.

이게 무슨 뜻이나면 만약 엄청 narrow한 local minima가 있다면 overfitting된 local minima일 확률이 높으므로 데이터를 더 많이 학습시켜주면 없어질 가능성이 큰 minima이다. 이 경우 벗어나는 것이 이상적이다.

하지만 주변이 평평한 local minima의 경우 충분히 일반화가 된 mimima일 가능성이 크다. 이 경우 overshooting되는 것은 우리가 원하지 않는 상황이다. 따라서 regularization을 통해 local minima 주위를 평평하게 만들어주는 작업과 더불어 overshooting을 방지하기 위한 알고리즘이 필요하다.

1.2-2 : Nesterov momentum

Nesterov는 overshooting을 해결하기 위해 고안된 optimizer이다.

1.3 curvature of loss function

1.3-1: AdaGrad

1.3-2 : RMSProp

1.4 Adam ( momentum + curvature of loss function)

1.5 Second order optimization

2. Regularization

큰 모델 사용 > overfitting 완화 methods

• Data 늘리기 방법
• 한 모델 안에서 regularization 방법
• 모델 여러개 혼합
• 아예 적은 data로도 잘 작동하게 하는 방법/ 생각의 전환

2.1 왜 큰 모델을 사용?

• data의 증가
• overfitting 방지니까

2.2 Data Augmentation

2.3 Improving single model

2.3-1 L1, L2 regularization

2.3-2 Dropout

2.3-3 Drop connect

2.3-4 Batch normalization

2.4 Ensemble

3. Transfer learning

• less data로 잘 작동하게 하는 방법