package task.gold.party1238;

import java.io.*;
import java.util.*;

public class Main {
    static BufferedReader br;
    static BufferedWriter bw;
    static StringTokenizer st;
    static int N;
    static int M;
    static int X;
    static List<List<Road>> map;
    static int[] dp;
    static boolean[] visited;
    static int INF = 987654321;
    static int[] result;

    public static void main(String[] args) throws IOException {
        br = new BufferedReader(new InputStreamReader(System.in));

        // 첫 줄 파싱
        st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken()); // 학생 수(노드)
        M = Integer.parseInt(st.nextToken()); // 도로 수(엣지)
        X = Integer.parseInt(st.nextToken()); // 도착지

        setMap();
        result = new int[N+1];

        for (int i = 1; i <= N; i++) {
            int GoExp = dijkstra(i, X);
            int comebackExp = dijkstra(X, i);
            result[i] = GoExp + comebackExp;
        }

        // INF값들 삭제 해주기
        for (int i = 0; i < dp.length; i++) {
            if (result[i] > 98765432) {
                result[i] = 0;
            }
        }

        // Max값 찾기
        int maxNodeValue = result[1];
        for (int i = 1; i < result.length; i++) {
            if (result[i] > maxNodeValue) {
                maxNodeValue = result[i];
            }
        }

        bw = new BufferedWriter(new OutputStreamWriter(System.out));
        bw.write(""+maxNodeValue);
        bw.flush();
        bw.close();
        br.close();

    }
    private static int dijkstra(int start, int target) {
        dp = new int[N+1];
        visited = new boolean[N+1];
        Arrays.fill(dp, INF);

        dp[start] = 0;

        for (int i = 0; i < N; i++) {

            int min = dp[0];
            int minIndex = 0;

            for (int j = 0; j < dp.length; j++) {
                if (dp[j] < min && !visited[j]) {
                    min = dp[j];
                    minIndex = j;
                }
            }

            visited[minIndex] = true;

            for (Road road : map.get(minIndex)) {
                dp[road.end] = Math.min(dp[road.end], dp[minIndex] + road.exp);
            }
        }

        return dp[target];

    }

    private static void setMap() throws IOException {
        // map 만들기
        map = new ArrayList<>();

        // 시작점 확보
        for (int i = 0; i <= N ; i++) {
            map.add(new ArrayList<>());
        }

        // 도로 정보 주입
        for (int i = 1; i <= M; i++) {
            st = new StringTokenizer(br.readLine());
            int start = Integer.parseInt(st.nextToken());
            int end = Integer.parseInt(st.nextToken());
            int exp = Integer.parseInt(st.nextToken());

            map.get(start).add(new Road(end, exp));
        }
    }

    static class Road {
        int end;
        int exp;

        public Road(int end, int exp) {
            this.end = end;
            this.exp = exp;
        }

        @Override
        public String toString() {
            return "Road{" +
                    "end=" + end +
                    ", exp=" + exp +
                    '}';
        }
    }
}

• 그래프 문제임을 확인, 최단경로 문제임을 확인, 음의 간선 없음 확인 -> 다익스트라
• 인접연결리스트로 구현 -> 시간 줄이기용

다익스트라

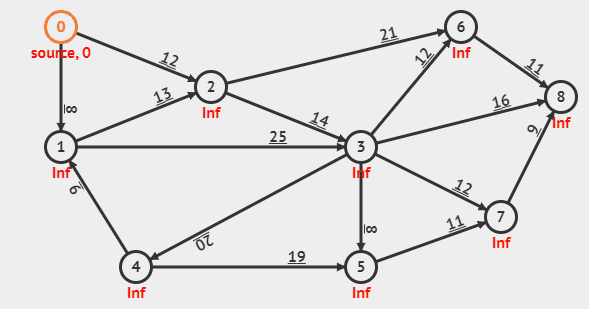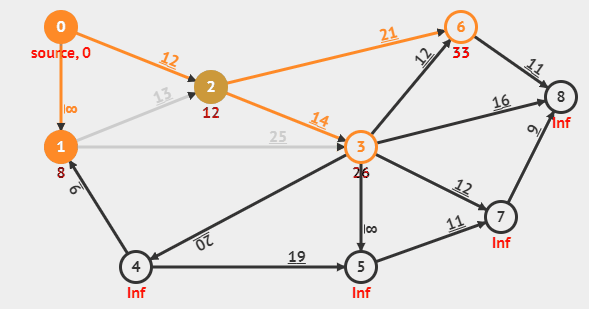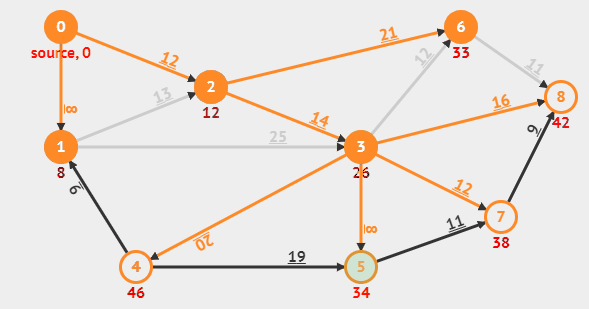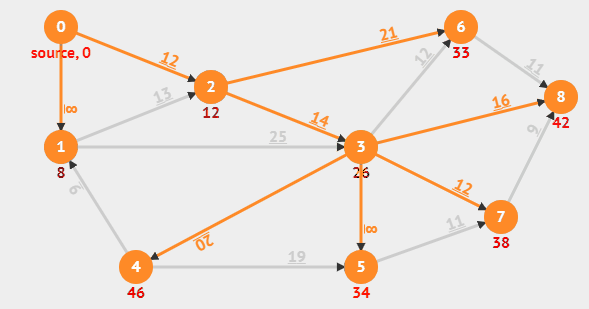
start 노드 설정만 필요, 음의 간선 없어야 함, 최단 경로 문제여야 함.

dp는 모두 INF값으로 초기화후 start 인덱스에만 0부여
start 노드에서 뻗어나가는 간선을 체크하여 dp(노드 비용 담은)에 업데이트
dp(체크한 간선의 도착) = Min(dp(체크한 간선의 도착), dp(체크한 간선의 시작) + 간선의 비용) 으로 업데이트 한다. 그 후 unvisited인 노드들 중 최솟값을 가지는 노드들에 대하여 위 과정 반복.

모든 반복이 끝나면 start에 대한 나머지 노드들의 최단 경로가 dp에 나타남.

문제에서는 X라는 특정한 도착지점을 설정했고 dp(X)를 파티에 가기 위한 최소비용으로 변수를 따로 뽑아놓고 X를 시작점으로 다시 다익스트라를 돌려 dp(본인노드)로 파티에서 되돌아오는 최소비용을 얻음

파티 가는거 + 파티에서 오는거 = 노드의 파티 놀러갔다 오는 왕복 최단거리

모든 노드에 대해 실행. -> 노드들의 왕복 최단거리들 중에서 INF들은 모두 0으로 만들고 나머지 중에 max값 찾기.