package task.gold.warmhole1865;

import java.io.*;
import java.util.*;

public class Main {
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
    static StringTokenizer st;
    static final int INF_VALUE = 9000001;

    public static class Edge {
        int start;
        int end;
        int exp;

        public Edge(int start, int end, int exp) {
            this.start = start;
            this.end = end;
            this.exp = exp;
        }

        @Override
        public String toString() {
            return "Edge{" +
                    "start=" + start +
                    ", end=" + end +
                    ", exp=" + exp +
                    '}';
        }
    }

    public static void main(String[] args) throws IOException {
        int TC = Integer.parseInt(br.readLine());

        int[] dp;
        Map<Integer,List<Edge>> map;
        StringBuilder sb = new StringBuilder();

        for (int i = 0; i < TC; i++) {
            st = new StringTokenizer(br.readLine());
            int N = Integer.parseInt(st.nextToken()); // 지점 수
            int M = Integer.parseInt(st.nextToken()); // 도로 개수
            int W = Integer.parseInt(st.nextToken()); // 웜홀 개수
            // 메모리 초기화
            map = new HashMap<>();
            dp = new int[N+1];
            for (int j = 1; j <= N; j++) {
                map.put(j, new ArrayList<>());
            }
            // 데이터 초기화
            for (int j = 0; j < M; j++) {
                st = new StringTokenizer(br.readLine());
                int start = Integer.parseInt(st.nextToken());
                int end = Integer.parseInt(st.nextToken());
                int exp = Integer.parseInt(st.nextToken());
                map.get(start).add(new Edge(start, end, exp));
                map.get(end).add(new Edge(end, start, exp));

            }

            for (int j = 0; j < W; j++) {
                st = new StringTokenizer(br.readLine());
                int start = Integer.parseInt(st.nextToken());
                int end = Integer.parseInt(st.nextToken());
                int exp = -Integer.parseInt(st.nextToken());
                map.get(start).add(new Edge(end, start, exp));
            }

            sb.append(bellmanford(map, dp, N) ? "YES\n" : "NO\n");

        }
        bw.write(sb.toString());
        bw.flush();
        bw.close();
        br.close();
    }

    private static boolean bellmanford(Map<Integer,List<Edge>> map, int[] dp, int N) {

        for (int i = 1; i <= N; i++) {
            dp[i] = INF_VALUE;
        }
        boolean updated = false;

        dp[1] = 0; // 시작점 설정

        // N-1 반복
        for (int i = 0; i < N-1; i++) {
            updated = false;
            // 모든 노드 조사
            for (int j = 1; j <= N; j++) {
                for (Edge edge : map.get(j)) {
                    if (dp[edge.end] > dp[edge.start] + edge.exp) {
                        updated = true;
                        dp[edge.end] = dp[edge.start] + edge.exp;
                    }
                }
            }

            if (!updated) {
                break;
            }
        }

        if (updated) {
            for (int j = 1; j <= N; j++) {
                for (Edge edge : map.get(j)) {
                    if (dp[edge.end] > dp[edge.start] + edge.exp) {
                        return true;
                    }
                }
            }
        }
        return false;

    }
}

벨만포드 알고리즘

• 그래프에서 Edge가 어떻게 형성되있는가랑 상관없이(그냥 완전연결 그래프라고 생각하자) Start 노드에서 임의의 목적지 노드까지 "순환 없이" 가는 과정에서 Edge를 MAX로 통과하는 수는 모든 노드 수 - 1이다.

만약 노드가 8개인 그래프에서 1번 노드를 출발하여 8번 노드까지 도착할 때 까지 8개의 노드를 거쳤다면 이는 분명 순환이 존재한다.

일단 이를 잘 기억하자.

음의 순환 문제

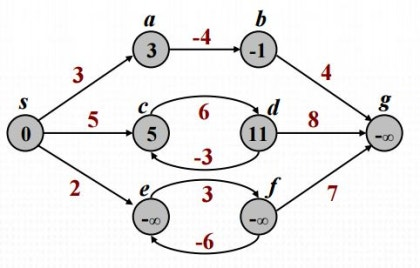위의 그래프에서 s에서 g로 가는 최소비용 거리는 어떻게 될까. 최소비용은 마이너스 무한대이다. s -> e -> f -> e -> f ...... 의 경우 때문이다.
음의 가중치 간선이 존재할 때 음의 순환 문제가 발생 가능하다.

만약 최소비용 루트를 구하는데 간선의 가중치가 모두 양수라면 순환이 일어나는 것은 피해야 하기에 순환의 경우의 수는 버리게 된다.

즉 그래프의 최단경로 문제에서 음의 간선이 존재하고 사이클이 존재할 때 우리는 최단 경로를 잡을 수 없다. 음의 꼭짓점이 존재하지 않고 발산해버리기 때문이다.

벨만포드 알고리즘의 목적

벨만포드 알고리즘은 음의 가중치 그래프의 최단경로 문제에서 음의 순환의 존재를 찾을 수 있다. 다익스트라와 비슷하지만 음의 가중치 그래프에서 발생하는 문제를 찾을 수 있다.(다익스트라는 음의 순환을 찾을 수 없음

구현

임의의 start를 설정해도 되고 문제에서 지정해주어도 상관 없다. 각 노드마다 비용을 계산할 메모리를 확보해놓고 모든 노드를 서치한다. (메모리는 시작노드를 제외하고는 모두 양의INF 값으로 둔다.)

모든 노드를 서치하는 목적은 모든 간선을 서치하기 위함이다.

1. start노드부터 start노드에 붙어있는 간선들을 조사한다.
2. 간선들의 도착노드(메모리에서 해당 노드들은 양의 무한대로 초기화 되어있음)의 메모리 값을 다음 기준으로 업데이트한다.
3. 간선의 도착노드 메모리 값 = min(간선의 도착 노드 메모리 값, 간선의 시작노드 메모리 값 + 간선의 비용)
4. 모든 노드를 돌며 모든 간선을 보며 업데이트를 했다면 1~3 과정을 N-2번 더 해준다.(총 N-1번 해준다고 보면 된다. => N-1번의 Loop를 돌린다)

5. N-1번의 루프를 진행하다가 한번도 업데이트가 안 일어난다면 모든 루프를 종료한다.(음의 순환이 없다는 것이다)
6. N-1번째 루프까지 업데이트가 일어났다면 N번째까지 시도한다. 만약 N번째에서 업데이트가 일어난다면 음의 순환이 존재하고 N번째에서 일어나지 않는다면 음의 순환이 존재하지 않는다.

• N+1, N+2.... 는 안봐도 된다.