새와 비행기 구별하기: 이미지 학습

6장에서는 경사 하강을 통해 내부 동작을 이해하고, 파이토치가 제공하는 기능을 활용해 모델을 만들고 최적화 해보았다. 7장에서는 이미지를 통해 신경망에 대한 기초를 더 다져본다.

작은 이미지를 모아 놓은 데이터셋

CIFAR-10 데이터셋은 지난 십여 년간 컴퓨터 비전의 고전이 되어 왔다. 이 데이터셋은 32x32 크기의 RGB 이미지 6만 개로 구성되어 있으며 1에서 10까지의 정수 레이블이 매겨져 있다. 각각은 비행기, 자동차, 새...말, 배, 트럭을 뜻한다. torchvision을 통해 데이터셋을 내려받고 파이토치 텐서 컬렉션으로 읽어들이도록 한다.

from torchvision import datasets
data_path = '../data-unversioned/p1ch7/'
cifar10 = datasets.CIFAR10(data_path, train=True, download=True) # <1>
cifar10_val = datasets.CIFAR10(data_path, train=False, download=True) # <2>

첫번째 인자는 데이터를 받을 위치, 두번째 인자는 훈련셋인지 검증셋인지, 세번째 인자는 경로에서 데이터를 찾을 수 없으면 자동으로 웹에서 다운로드 받아주는 인자이다.

데이터 변환

이제 PIL 이미지를 파이토치 텐서로 변환할 단계이다. 현재 데이터셋 객체인 cifar10은 다음과 같이 torchvision의 속성으로 구성되어있다. 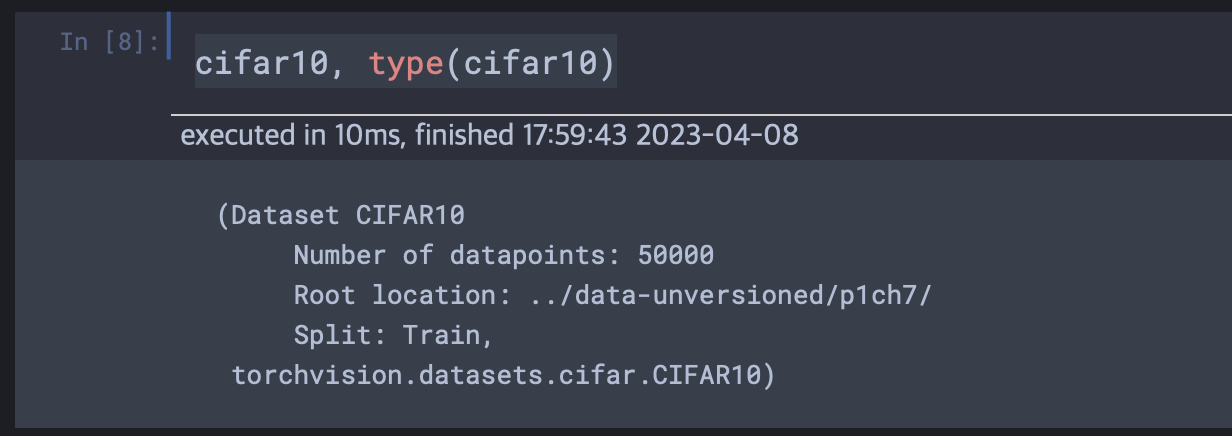transforms모듈 내의ToTensor 메서드는 넘파이 배열과 PIL이미지를 텐서로 바꾸는 역할을 한다. 뿐만 아니라 출력 텐서의 차원을 CxHxW로 맞추어준다.

from torchvision import transforms

to_tensor = transforms.ToTensor()
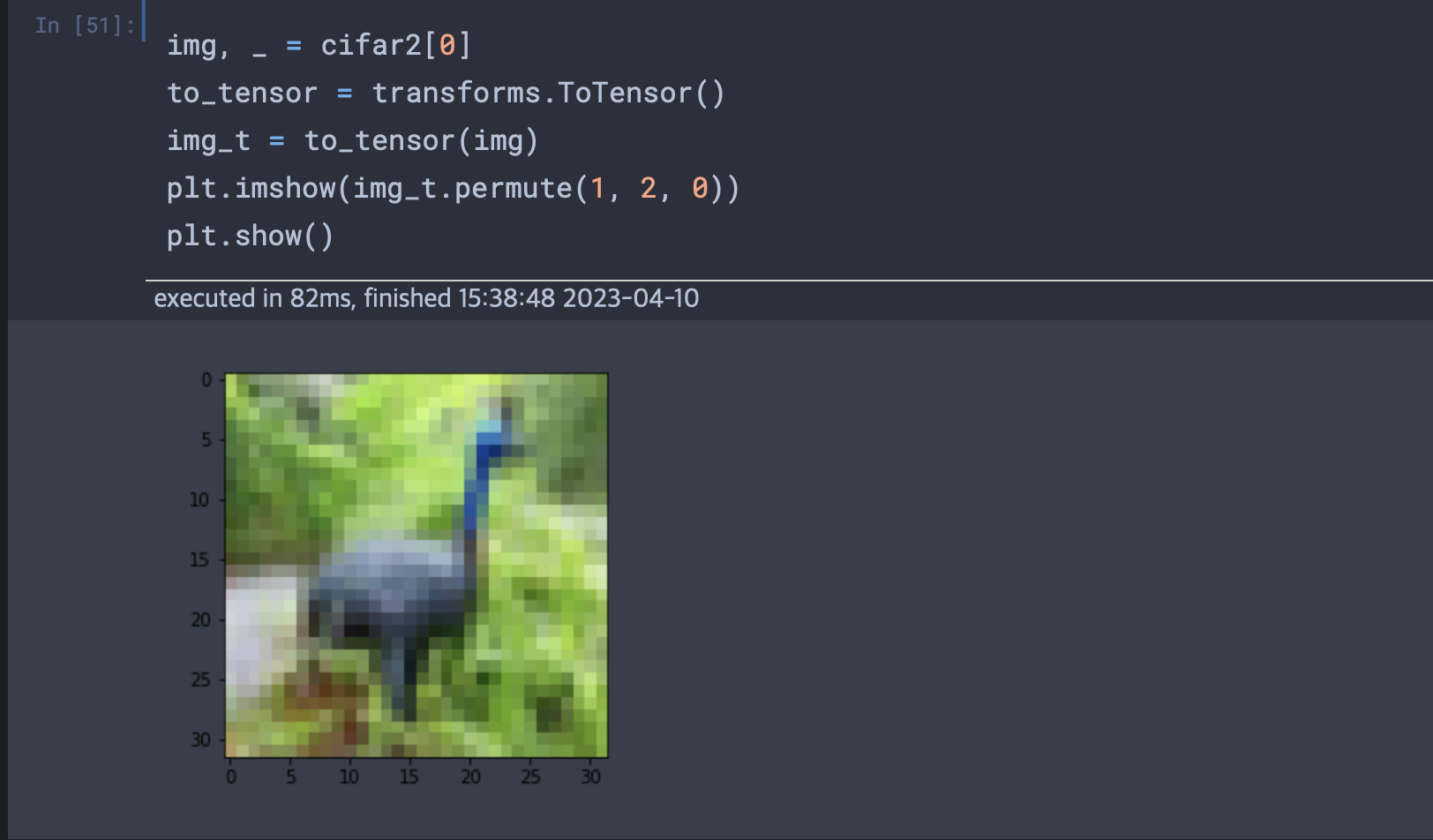
img_t = to_tensor(img)
img_t.shape

이미지는 해당 코드를 통해 3x32x32 텐서로 바뀌었다.(img변수는 하나의 데이터를 가지고 있음.)

데이터 정규화

transforms.Compose를 활용하면 여러 변환을 엮어서 사용할 수 있다. 또한 데이터 증강(data augmentation)과 데이터 로딩을 함께 수행 가능하다. 데이터셋 정규화를 통해 각 채널이 평균값 0과 단위 표준 편차를 가지게 만들 수 있다. transforms.Normalize는 (v[c] - mean[c]) / stdev[c])의 변환을 적용시켜주며, mean과 stdev는 따로 계산을 수행해야한다.

모든 데이터를 텐서화를 먼저 진행한다.

tensor_cifar10 = datasets.CIFAR10(data_path, train=True, download=False,
                          transform=transforms.ToTensor())

imgs = torch.stack([img_t for img_t, _ in tensor_cifar10], dim=3)
imgs.shape
# 결과 : torch.Size([3, 32, 32, 50000])

채널별로 평균, 표준편차를 계산하고 Normalize메서드에 해당 값들을 넣어준다. (책에서는 직접 숫자를 넣었지만 텐서로 넣어도 상관없다.)

imgs.view(3, -1).mean(dim=1) 
# view메서드를 통해 (3,32,32,50000) 을 (3, ??)로 바꾸어줌.
# (3, ??)을 두번째 차원기준으로 평균한다. 즉 (3)이 된다.
imgs.view(3, -1).std(dim=1)
# 같은 방식으로 std도 구하기

텐서화 뿐만아니라, 정규화기능도 넣어서 데이터를 불러오도록 코드를 수정한다.

transformed_cifar10 = datasets.CIFAR10(
    data_path, train=True, download=False,
    transform=transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize(imgs.view(3, -1).mean(dim=1),
                             imgs.view(3, -1).std(dim=1))
    ]))
# 여전히 transfromed_cifar10은 텐서객체는 아니다.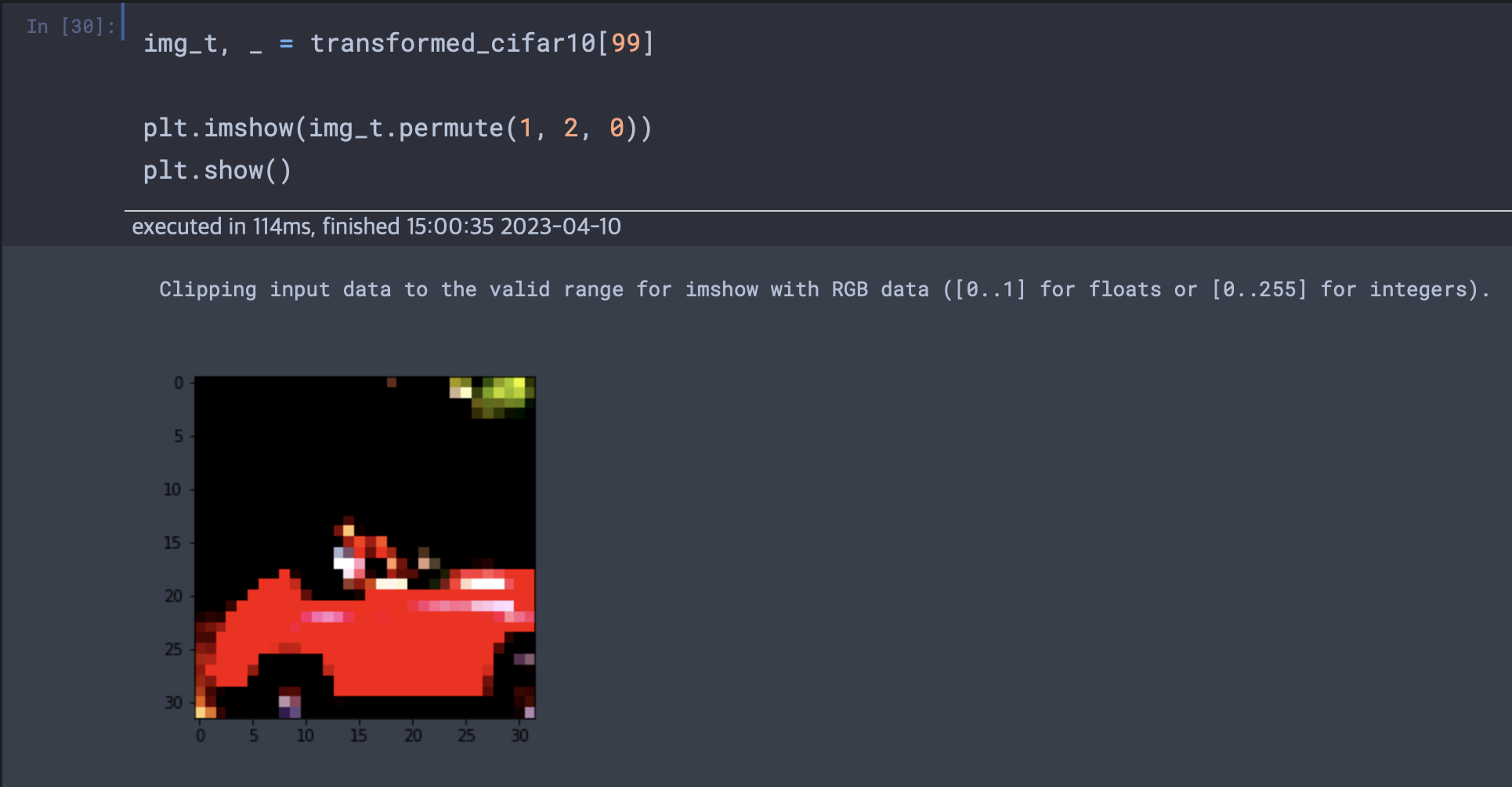

새와 비행기를 구별하기

조류 관찰 클럽이 카메라를 통해 자동적으로 카메라에 무언가 들어오면 바로 찍어서 실시간 탐조 블로그에 업로드하게끔 되어있으나, 그것이 비행기이든 새이든 상관하지 않을 때 이들은 다시한번 수정의 과정을 거쳐야한다.(비행기를 사진에서 삭제)

데이터셋 구축

우리가 필요한 것은 새와 비행기 데이터이다. cifar10에 이 두 데이터가 존재하니 cifar10에서 데이터를 필터링하면 될 것이다.

label_map = {0 : 0, 2: 1}
class_names = ['airplane', 'bird']
cifar2 = [(img, label_map[label])
         for img, label in cifar10 if label in [0, 2]] 
# 이미지와 레이블을 튜플로 묶어 리스트로 구성한다
cifar2_val = [(img, label_map[label])
         for img, label in cifar10_val if label in [0, 2]] 
# validation또한 동일하게.

완전 연결 모델

첫 시도는 사진데이터를 1차원으로 펼쳐 벡터로 늘어뜨려 신경망에 주입하는 것이다. 사진당 3x32x32이므로 우리는 3072개의 피처를 주입하는 것이다.

import torch.nn as nn

n_out = 2

# Linear층에 3072개의 입구를 만들고 출력으로 512개를 빼서 Tanh층에 넣어주고 Tanh층에서 나온 512개를 
# 다시 Linear층에 512개의 입구를 통해서 내부에서 처리되고 2개의 출력클래스로 나오게 한다.

model = nn.Sequential(
        nn.Linear(
        3072,
        512,
        ),
        nn.Tanh(),
        nn.Linear(
        512,
        n_out,)
)

여기서 잠깐 완전 연결 모델이란?
완전 연결이란 "Fully connected"의 해석이며, 완전 연결 층은 "Dense layer"라고도 일컫는다. 의미적으로는 한 층의 모든 뉴런이 다음 층과 모두 연결되있다는 뜻이다. 이미지에 입각하여 정확환 과정을 설명한다면,
1. 2차원 배열의 이미지 데이터를 1차원으로 평탄화
2. 아핀 변환후 활성화 함수를 통과하여 다음 입력으로
3. 최종적으로 softmax를 통해 분류

합성곱 연결층 vs 완전연결층
완전연결층은 1차원으로 평탄화 하는 과정에서 공간정보가 무시된다. 2차원 배열을 쭉 늘어뜨리다보니 직감적으로도 양옆의 데이터는 가깝지만 위아래 데이터의 거리는 멀어진다. 그렇다면 계산의 관점에서는 어떨까?
완전연결층은 입력과 출력뉴런이 모두 연결되어있다. 즉 입력x출력 뉴런수만큼의 가중치가 생길 것이고 이것은 학습내내 업데이트 되어야 하므로 엄청난 연산을 요구한다. 하지만 합성곱의 경우 필터가 가중치의 역할을 하기 때문에 비용이 줄어들게 된다.

실습에서 출력 뉴런의 수를 줄이는 이유는?

• 모델에서 출력 차원을 줄이는 이유는 여러 가지가 있다. 가장 대표적인 이유는 모델의 복잡도를 줄이기 위해서이다. 출력 차원이 크면 해당 층에서 다루는 정보가 많아지기 때문에, 층의 복잡도가 높아지고 모델 전체의 복잡도도 높아지게 된다. 이는 과적합(overfitting)의 위험성을 높이는 원인이 될 수 있다. 따라서 출력 차원을 줄이면 모델의 복잡도를 제어하고 일반화 성능을 향상시키는 효과를 얻을 수 있다.
• 또한, 출력 차원을 줄이면 파라미터 수도 감소한다. 이는 과적합 외에도 모델의 계산 복잡도를 줄여서 학습 속도를 빠르게 하고, 모델이 작은 메모리를 가진 디바이스에서도 사용할 수 있게 만든다.
• 마지막으로, 출력 차원을 줄이는 것은 특성 추출(feature extraction)의 관점에서도 중요하다. 출력 차원이 작은 층은 입력 데이터에서 중요한 특성만을 추출하고 나머지는 버리는 역할을 하게 된다. 이는 불필요한 정보를 제거하고 핵심 정보를 추출하는 효과를 가지며, 이후의 층에서 더 좋은 성능을 발휘할 수 있도록 도와준다.

분류기의 출력

우리는 n_out = 1을 출력하게 만들고 레이블을 부동소수점 수로 변환하여 MSELoss의 타깃으로 사용하여 회귀 문제로 풀 수 있지만, 우리는 출력값이 카테고리임을 알 수 있다.(이전 온도변환 문제랑 다르다는 것을 인지) 출력값은 새 혹은 비행기일 뿐이다.
즉 원핫인코딩으로 바꾸어 주어야 한다. 이상적인 경우 신경망은 비행기사진에 대해 torch.tensor([1.0, 0.0])을 출력하고 새에 대해서는 그 반대를 출력해야한다. 실제로의 분류는 완벽하지 않기에 두 값 사이의 값들이 분포할 것이다.

• 출력 값의 요소가 가질 수 있는 값은 [0, 1]범위로 제한된다.
• 모든 출력 요소의 값의 합은 1.0이다.

출력을 확률로 표현

소프트맥스는 벡터값을 받아 동일한 차원의 다른 벡터를 만든다. 또한 값이 확률로 표현되어야 하는 제약을 만족한다.
Softmax(소프트맥스)는 입력받은 값을 출력으로 0~1사이의 값으로 모두 정규화하며 출력 값들의 총합은 항상 1이 되는 특성을 가진 함수이다.
소프트맥스는 벡터의 각 요소 단위로 지수 연산(exp) 후 각 요소를 지수 값의 총합으로 나눈다.(이해를 위해 아래 그래프 제시)

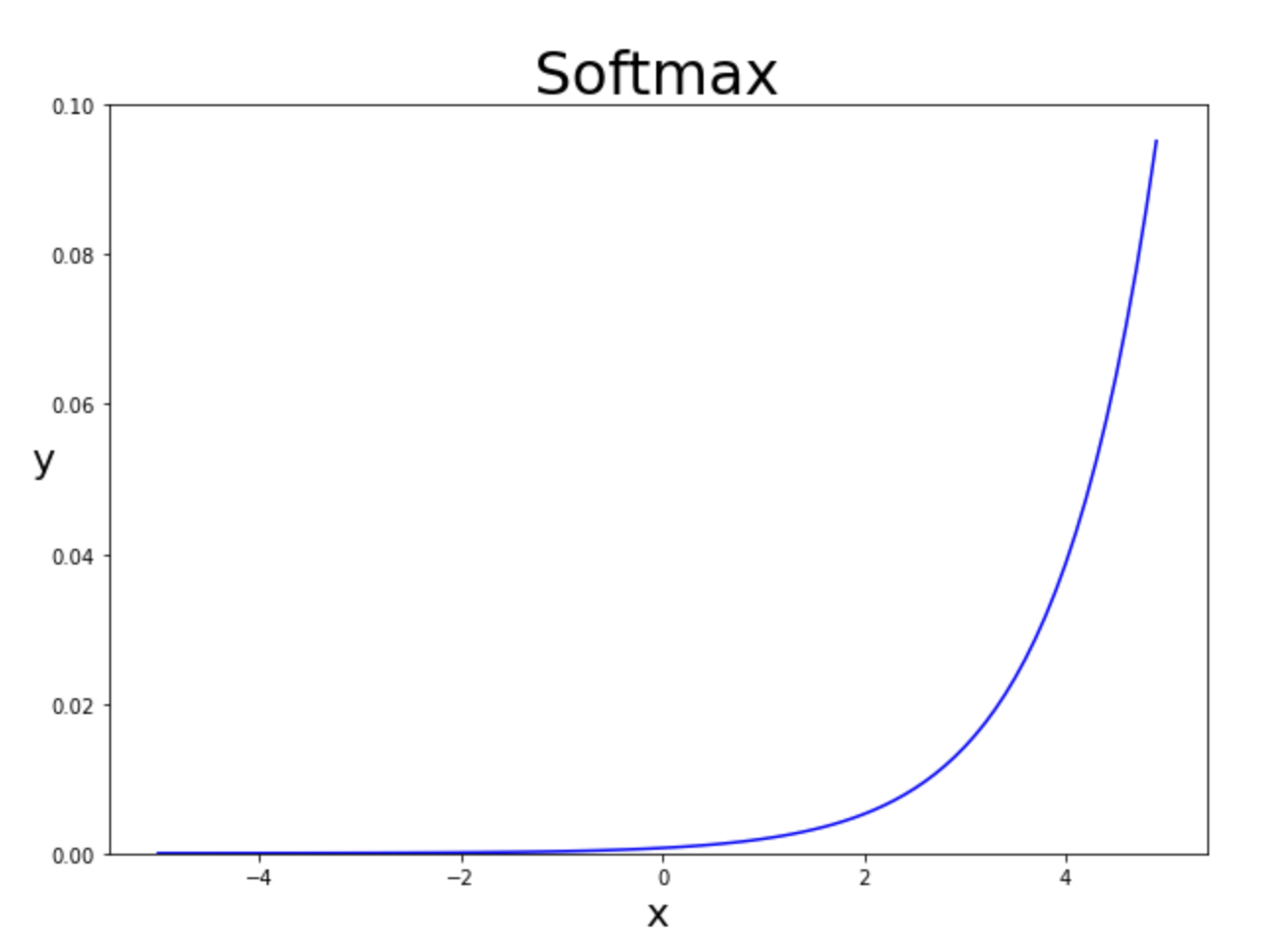소프트맥스는 단조 함수(증가함수)이므로 입력값이 낮아지면 출력값도 따라 낮아진다. 하지만 각 값들간의 비율을 맞춰주지는 않는다. 즉 입력이 2와 4 즉 두배차이가나는 입력값에 대해 출력값또한 두배차이를 발생시키지 않는 것이다.(선형함수가 아니니까 당연하겠지)

model = nn.Sequential(
        nn.Linear(
        3072,
        512,
        ),
        nn.Tanh(),
        nn.Linear(
        512,
        n_out,),
        nn.Softmax(dim=1) # 마지막에 소프트맥스 층 추가
    
)

모든 데이터셋에 대한 훈련전에 단일 데이터에 대해 적용해본다.
현재 모델의 파라미터들은 전혀 훈련되지 않은 상태이다. 현재는 두개의 확률 값에 대한 클래스를 알고 있지만, 신경망에서는 이를 표현하지 않는다. 레이블에서 0번 인덱스가 비행기, 1번인덱스가 새로 주어졌다면, 이게 출력값이 의미하는 순서가 된다. 이를 가지고 훈련 후 argmax연산을 통해 레이블을 얻어낼 수 있다. argmax는 제일 높은 확률에 대한 인덱스이다. torch.max는 해당 차원에서 가장 높은 요소와 인덱스를 리턴한다.

분류를 위한 손실값

현재 우리는 완전연결모델을 만들고(Linear - Tanh - Linear) 마지막 층에 클래스 확률 추출을 위해 소프트맥스 층을 추가하였다. 또한 데이터는 cifar10에서 텐서,정규화를 거치고 새와 비행기만 필터링하였다. 그 후 훈련되지 않은 모델에 텐서화 되어진 사진데이터를 넣어 작동하는지를 확인했다.

우리는 이제 전체데이터를 넣기 전에 모델의 훈련과정을 정의해야한다. 그러기 위해서는 손실 알고리즘을 정의해야 한다.

우리는 5, 6장에서 손실값으로 평균제곱오차(MSE)를 사용했다. 이를 사용하면 출력 확률이 [0, 1]혹은 [1,0]에 수렴하게끔 만들 수 있다. 하지만 우리는 이것이 중요하지 않다. 그 이유는 더 높은 확률에 대해 해당 클래스를 부여하기 때문에 1을 만드는 것이 중요한 것이 아니라 "우위"를 만드는 것이 중요하다. 즉 우위에 대한 답만 잘 내어준다면, 좋을 것이다. 즉 분류가 어긋날 경우(우선순위 틀림)에 대해서 벌점을 주고 싶다.

out이 "비행기"인 경우 클래스가 0을 나타내고 "새"인 경우 1을 나타내는 벡터라고 할 때 out에 속한 정답 클래스와 관련된 확률(가능도, likelihood)을 "극대화"할 필요가 있다. 즉 가능도가 낮을 때(상대적으로 애매한 확률)값이 커지는 손실함수가 필요하다. 반대로 가능도가 클 경우 손실값은 낮아야 한다. 이 경우에 대한 손실함수가 NLL 함수이다.

• NLL함수 표현식 : -sum(log(out_i[c_i])) sum은 N개의 샘플 합이고 c_i는 샘플 i에 대한 정답 클래스이다.
  이 함수는 지수적으로 감소하는 미분가능한 감소함수이다.

요약하면 분류를 위한 손실은 다음과 같이 계산된다.
1. 순방향 전달 후 마지막 선형 계층에서 출력값을 얻는다.
2. 이들의 소프트맥스 값을 계산하여 확률을 얻는다.
3. 정답 클래스와 일치하는 예측 확률값을 얻는다. 실측값도 존재한다.
4. 실측값을 통해 NLL값을 계산하여 손실값에 더한다.

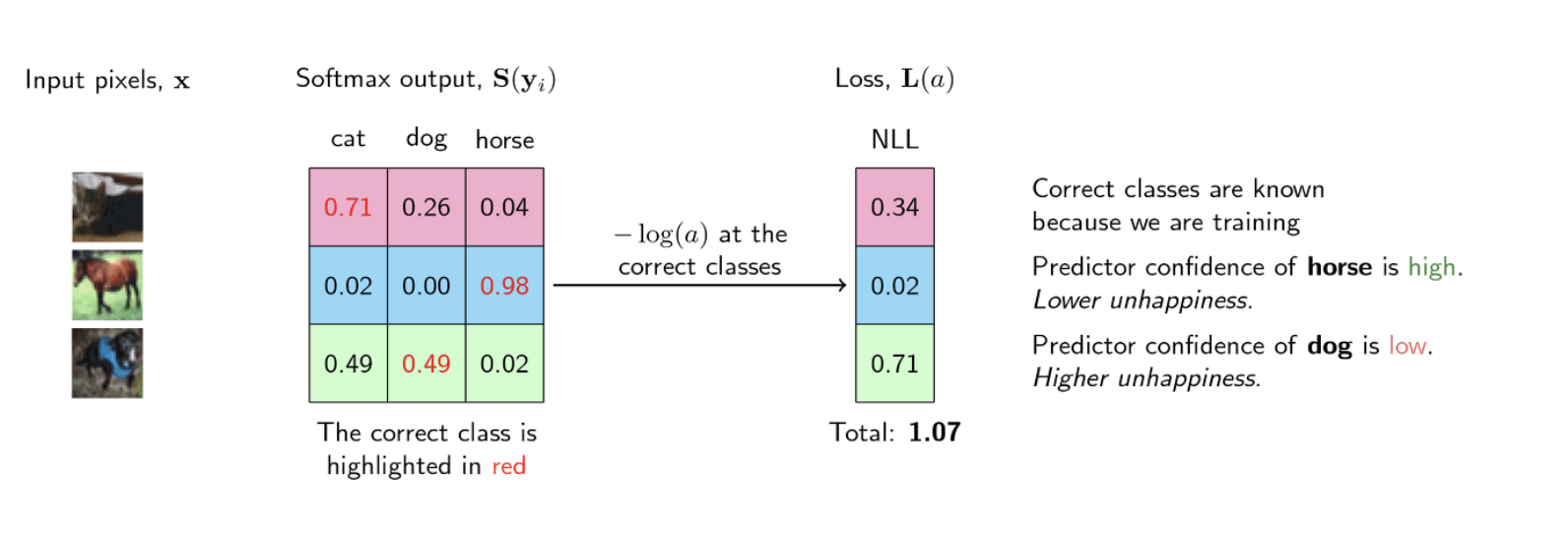
• Likelihood 를 최대화(Maximizing) 하는 것은 Log-likelihood 를 최대화(Maximizing) 하는 것과 동일합니다.
• 이를 반대로 뒤집으면 Likelihood 를 최대화 하는 것은 Negative * * likelihood 를 최소화 하는 것과 동일합니다.
• 그리고 Negative likelihood 를 최소화 하는 것은 Negative Log-Likelihood 를 최소화 하는 것과 동일합니다.
• 즉, Negative Log-Likelihood를 최소화 하는 것은 Likelihood를 최대화 하는 것과 동일한 효과를 가집니다.

즉 정리하면, 각 클래스에 대한 소프트맥스 값들이 생성되고, 로그화된다. 로그화후 정답레이블에 해당하는 로그값들을 sum한다. 그리고 마이너스를 붙인다 이것이 Negative Log-Likelihood이며 이것을 최소화하는 것이 가능도를 최대화하는 효과와 동일하다.

분류기 훈련

# 첫번째 훈련
import torch
import torch.nn as nn
import torch.optim as optim

model = nn.Sequential(
            nn.Linear(3072, 512),
            nn.Tanh(),
            nn.Linear(512, 2),
            nn.LogSoftmax(dim=1)
)

learning_rate = 1e-2

optimizer = optim.SGD(model.parameters(), lr=learning_rate)
loss_fn = nn.NLLLoss()

n_epochs = 100

for epoch in range(n_epochs):
    for img, label in cifar2:
        img = to_tensor(img)
        out = model(img.view(-1).unsqueeze(0))
        loss = loss_fn(out, torch.tensor([label]))
        
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
    
    print('Epoch: %d, Loss: %f' % (epoch, float(loss)))

다음과 같이 손실이 전혀 줄지 않는 모습을 보인다. (시간도 오래걸린다)(그 이전에 책에서 데이터 구성에 대한 코드가 잘못되어있다. cifar2에 대한 코드를 수정하였다. 정확히는cifar10이 normalize와 to_tensor을 포함하지 않은 데이터추출과정이었다.) 또한 loss 변수를 정의하는 부분에서 label은 이미 텐서인데 다시 텐서로 감는 것에서도 에러가 발생하였다.)

# 두번째 훈련
import torch
import torch.nn as nn
import torch.optim as optim


train_loader = torch.utils.data.DataLoader(cifar2, batch_size=64, shuffle=True)

model = nn.Sequential(
            nn.Linear(3072, 512),
            nn.Tanh(),
            nn.Linear(512, 2),
            nn.LogSoftmax(dim=1)
)

learning_rate = 1e-2

optimizer = optim.SGD(model.parameters(), lr=learning_rate)
loss_fn = nn.NLLLoss()

n_epochs = 100

for epoch in range(n_epochs):
    for imgs, label in train_loader: 
    # 이중리스트로 구성됨 [[텐서_imgs, 텐서_label], [텐서_imgs, 텐서_label],...]
        batch_size = imgs.shape[0] 
        # (64, 3 ,32 ,32)의 64가 batch_size가 됨.
        outputs = model(imgs.view(batch_size, -1))
        # (64, 3x32x32 = 3072)로 차원변경하여 model에 주입
        # (64 : 한 단위의 배치, 3072 : 입력 개수)
        loss = loss_fn(outputs, label)
        # loss계산 : outputs.shape = (64,2) label = (64)
        # 레이블에 해당하는 outputs 확률값을 모두 더함.
        optimizer.zero_grad()
        # 기울기 초기화
        loss.backward()
        # 기울기 계산
        optimizer.step()
        # 파라미터 수정단계(본래값 - lr x loss.backward())
        # 64개씩 50000개를 모두 해당 과정으로 소화하면, 하나의 에폭 끝
    print('Epoch: %d, Loss: %f' % (epoch, float(loss)))

DataLoader는 미니 배치의 데이터를 섞거나 구조화하는 작업을 돕는다. 이것을 활용하여 각 에포크마다 데이터를 고르게 섞은 후 고르게 샘플링한다. DataLoader객체는 batch_size와 suffle여부를 인자로 받게 된다. 이렇게 훈련을 진행한 결과 손실값이 이상적으로 작아지는 모습을 볼 수 있었다.

DataLoader 모듈 사용법
Step 1. dataset 생성
pytorch의 dataloader를 사용하기 위해서는 우선 필요한 input 벡터들이 적절히 묶인 형태로 데이터 셋을 만들어주어야 한다. 이 과정에는 zip 함수를 사용해도 되고, 파이토치에서 제공하는 TensorDataset 함수를 사용해도 된다.
Step 2. DataLoader 함수 설정
이후, DataLoader 함수에서 위에서 묶은 데이터 셋을 분할해줄 준비를 해주면 된다. 여러 가지 옵션을 지정할 수 있지만, 여기서는 1 step에 넣어줄 데이터의 개수를 정하는 batch_size 옵션과 순서를 섞어서 분할할지 여부를 정하는 shuffle 옵션을 지정한다.
Step 3. 순회를 통해 분할된 데이터 가져와 사용. DataLoader 객체는 일종의 generator 형태로, 인덱싱이 불가능하고 for문 순회 등의 방법을 통하여 분할된 데이터를 일일이 가져와야 한다.

nn.LogSoftmax와 nn.NLLLoss 조합은 nn.CrossEntropyLoss와 동일하다. NLLLoss는 입력으로 로그 확률 예측을 받는 반면, CrossEntropyLoss는 점수를 입력으로 받는다. 일반적으로는 신경망의 마지막 계층에서 손실값으로 크로스엔트로피손실값을 사용한다.

첫 번째 선형 모듈은 300만 개의 파라미터를 가진다. 이런 부분은 충분히 예상가능한데, 선형 계층의 수식인 y = w * x + bias를 생각해본다면 x의 길이가 3072(3x32x32, 입력의차원, 배치차원 무시)이고 y는 1024(출력의 차원)그렇다면 입력에서 출력으로의 연결선의 개수는 3072 x 1024개가 된다. 연결선 하나하나에는 가중치가 존재하고, 출력층에 도착한 값들은 다시 bias가 더해진다. 즉 1024번 다시 더해진다. 즉 3072 x 1024 + 1024가 되어 약 315만개의 파라미터가 첫 모듈에서 생성된다.

• 만약 1024 x 1024 RGB 이미지라면 처음 모듈에서만 12기가 램 영역이 필요하게 된다.(대략 30억개 파라미터 생성 및 연산됨)

# with 검증 loss 함께 계산
import torch
import torch.nn as nn
import torch.optim as optim



train_loader = torch.utils.data.DataLoader(cifar2, batch_size=64, shuffle=True)
val_loader = torch.utils.data.DataLoader(cifar2_val, batch_size=64, shuffle=True)
model = nn.Sequential(
            nn.Linear(3072, 512),
            nn.Tanh(),
            nn.Linear(512, 2),
            nn.LogSoftmax(dim=1)
)

learning_rate = 1e-2

optimizer = optim.SGD(model.parameters(), lr=learning_rate)
loss_fn = nn.NLLLoss()

n_epochs = 100

arr_val = []
arr_train = []

for epoch in range(n_epochs):
    for imgs, label in train_loader:
        batch_size = imgs.shape[0]
        outputs = model(imgs.view(batch_size, -1))
        loss = loss_fn(outputs, label)
        
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
    
    with torch.no_grad():
        
        loss_val = 0
     
        model.eval()
        for imgs, label in val_loader:
            batch_size = imgs.shape[0]
            out = model(imgs.view(batch_size, -1))
            loss_val += loss_fn(out, label)
        print('Epoch: %d, Validation_Loss: %f, Train_Loss: %f'  % (epoch, float(loss_val / 31.25), float(loss))) # 2000 / 64 = 31.25
        arr_val.append(loss_val)
        arr_train.append(loss)
        model.train()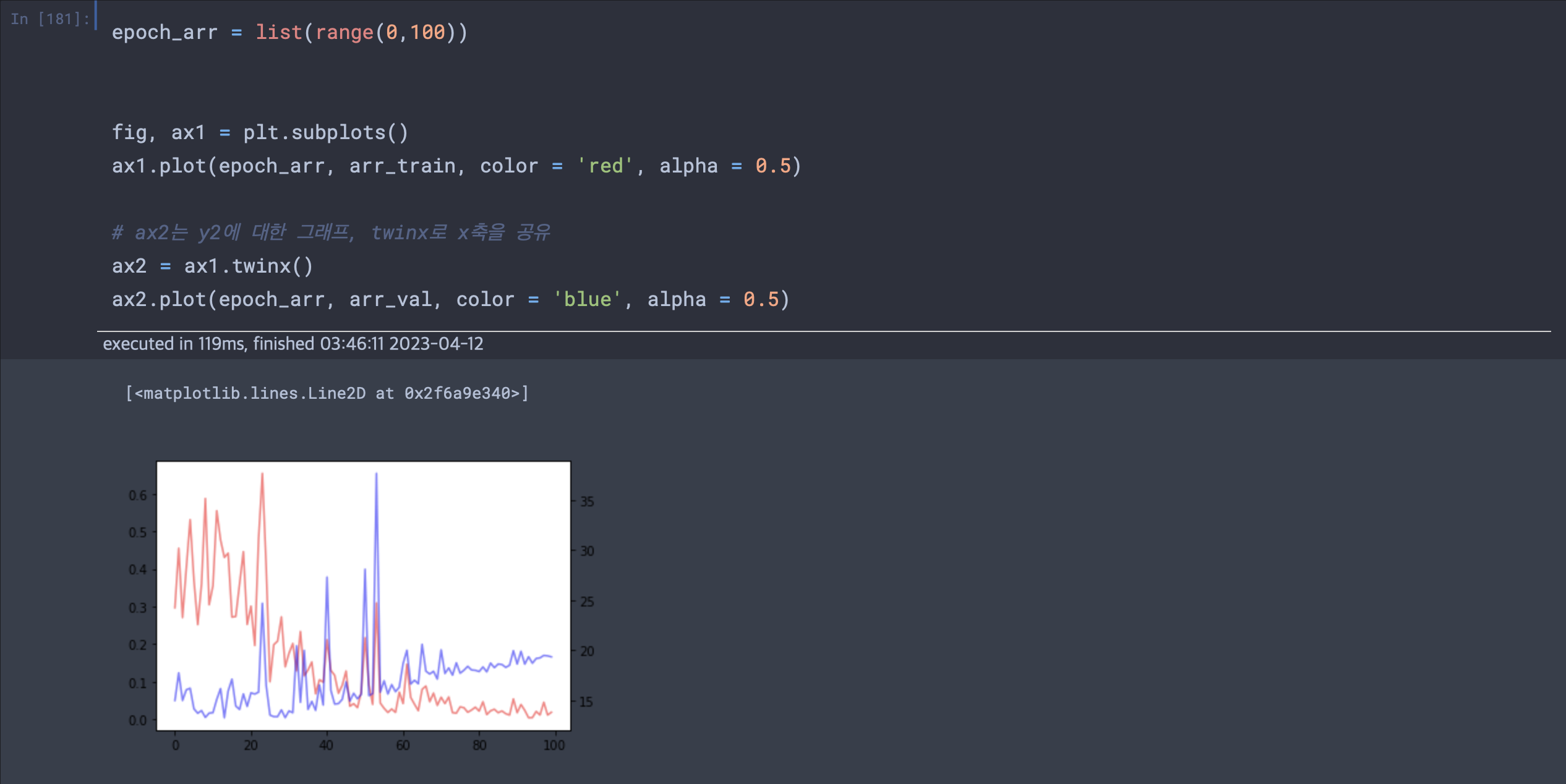

각 에폭마다 훈련손실과 검증손실을 누적하여 그래프화 한 것이다. 실제로 훈련손실은 계속해서 줄어들지만 검증손실의 경우 에폭이 30즈음부터 올라가는 모습을 볼 수 있다.

# 책은 데이터로더를 씀
total = 0
correct = 0

with torch.no_grad():
        for imgs, label in cifar2_val:
            out = model(imgs.view(-1).unsqueeze(0))
            _, predicted = torch.max(out, dim=1)
            total += 1
            correct += int(predicted == label)
            
print('Accuracy: {}'.format(correct/total))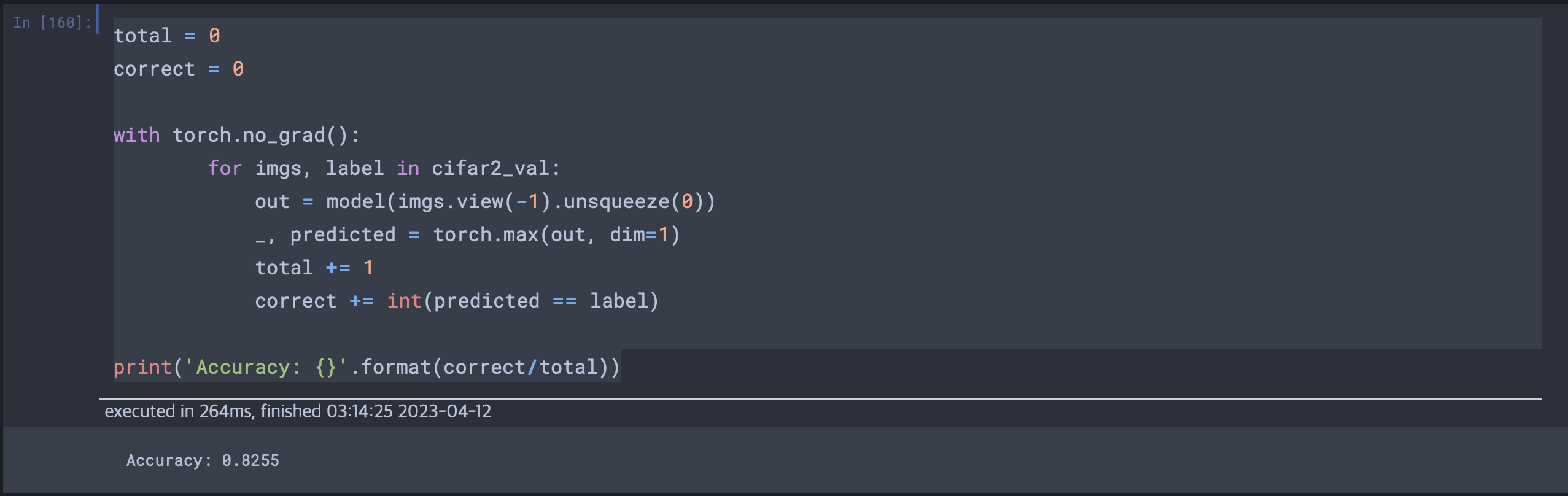

에폭이 100인 경우에 정확도가 다음과 같이 나왔다. 그렇다면 검증손실의 최소부분인 에폭이 30일 경우로 테스트해보면 결과는 다음과 같다.

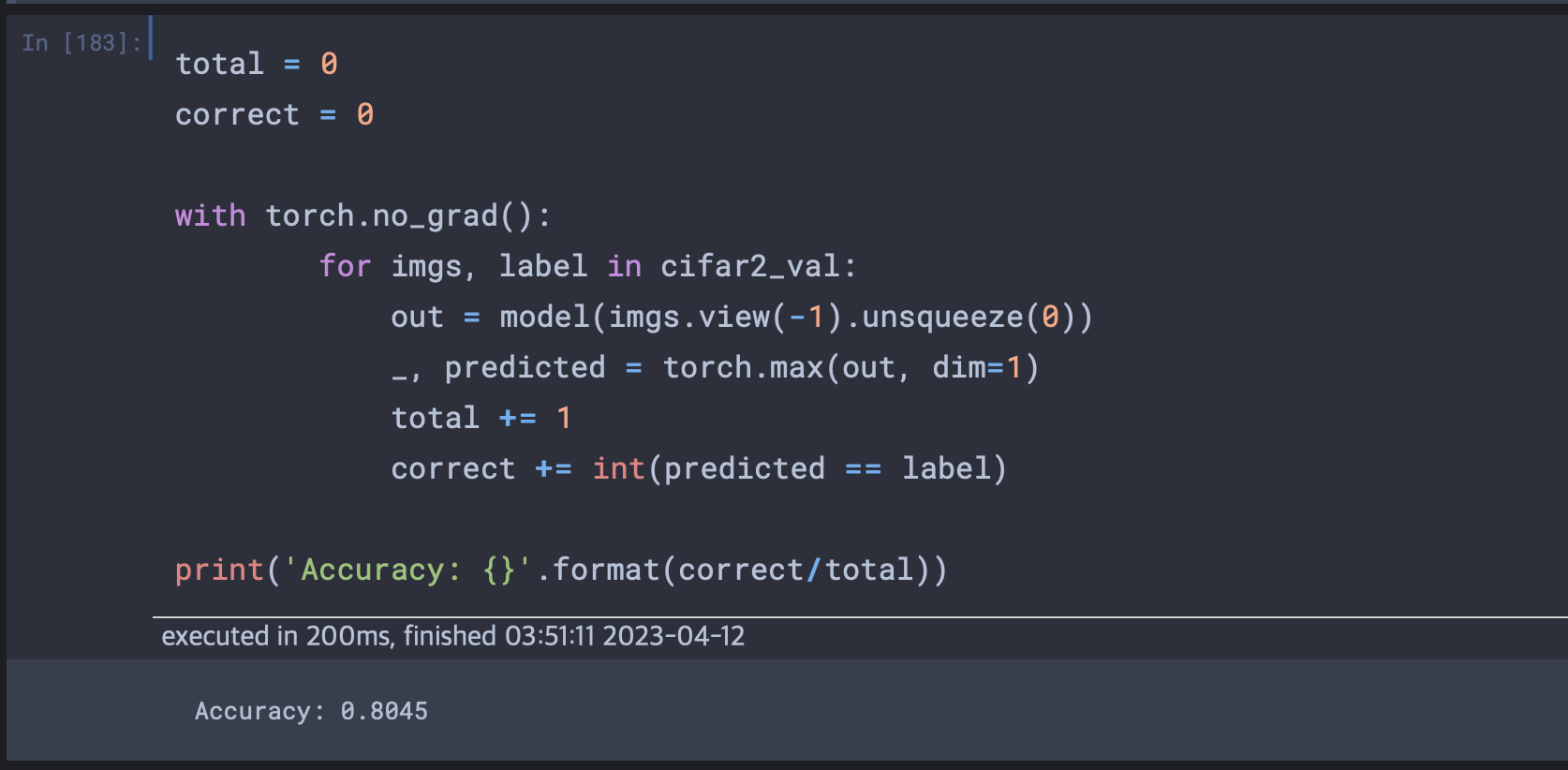
왜 개선 안됨?
실제로 검증 손실이 더 나은 구간에서 정확도를 측정했을 때 의미있는 개선 수치가 보이지 않았다. 이것이 뜻하는 바는 완전연결층의 뚜렷한 한계를 보이는 것이다. 즉, 현재 나타나는 절대적으로 높은 검증손실 수치는(훈련손실대비 10배이상) 완전연결층을 통해 훈련으로 만들어진 현재의 이미지 비전 모델이 훈련데이터가 아닌 새로운 데이터에 대해 유의미한 수준의 성능을 내지 못한다는 뜻이다. 즉 현재의 손실분포에서 최저 손실을 찾는 과정이 크게 의미가 없을 수 있다는 뜻이다.

완전 연결의 한계

현재 이미지를 1차원으로 놓고 선형 모듈을 사용하는 방식을 실습했다. 그러나 만약 학습된 하나의 사진이 픽셀 0,1은 어둡고 픽셀1,1도 하늘색으로 학습되었을 때 만약 비행기가 이동하여 픽셀 0,1과 1,1이 하늘색이 아닌 비행기의 요소의 색으로 구성된다면 각 픽셀간의 관계를 처음부터 다시 학습해야할 것이다.

즉 전문 용어로 완전 연결 신경망은평행이동 불변성(translation invariance)이 없다. 즉 완전 연결 신경망으로 비행기를 비교적 정확히 인식 학습시키기 위해서는 비행기가 사진 내에서 평행이동된 사진을 모두 학습해야할 것이다.(데이터 증강, data augmentation) 하지만 이러한 증강작업은 상당한 비용이 든다.