결정트리(DecisonTree) 알고리즘

jkky98·2023년 4월 15일

DataScience

목록 보기

20/26

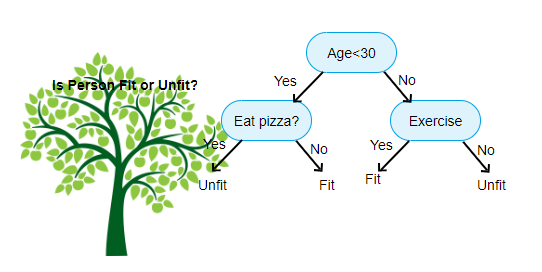
결정트리는 타겟값이 존재하는 지도학습이고, 결정트리의 예시는 위의 그림과 같다. 설명변수(descriptive variables)에 존재하는 특성의 특정 특성값(특정 기준)을 기준으로 분기가 진행되고 부모노드에서 두 개의 자식노드로 분기된다.(타 알고리즘에서는 다진트리(multi-way tree)로 구성되는 경우도 있다.

결정트리를 직접 구성한다고 했을 때 대부분의 포스팅들은 실습코드를 제시한다.(sklean등의 라이브러리를 활용) 사실 이것은 전혀 중요하지 않다. 이런 코드를 쓰고 실행하는 방법을 숙지하는 것은 학습에 의미가 존재하지 않는다.

결정트리의 원리

결정트리의 원리를 첫 문단으로 제시하는 경우가 많다. 하지만 결정트리의 처음 부터 끝까지 잘 이해하기 위해서는 다음과 같은 질문에 대답할 수 있어야한다.

결정 트리에서 분기를 위한 특성을 선택하는 방식은 무엇인가?
선택된 특성을 어떤 특성 값을 기준으로 데이터들을 분할할 것인가?

결정트리의 기본 근저의 개념은 분기 전과 후의 데이터의 혼잡도가 줄어들어야 한다. 즉 어떠한 기준으로 분기를 진행했다면, 분기 후 자식노드1과 자식노드2(두개의 자식노드로 분기되니까)는 분기 이전 부모노드일때보다 엔트로피가 낮아져야 한다.

Entrophy

다음은 chat-gpt가 제시해준 하나의 예시이다.
이런 부모노드에 담긴 6개의 설명변수들이 존재한다고 가정하고, 성별에 대한 엔트로피를 계산한다면
Entrophy = -p(남)log(p(남)) - p(여)log(p(여))로 계산될 것이다.
(남 : 2/6 , 여 : 4/6)
엔트로피 계산식을 보면 로그안에 확률을 넣은 것을 확률에 곱해준다.

일단 우선 확률에 대한 생각을 해보자면, 확률은 0~1의 값을 가진다. 엔트로피는 불순도의 개념이기 때문에, 확률이 0%이거나 100%일 경우 매우 순도가 높은 즉 서로다른 것들이 섞이지 않았다는 것이니 엔트로피는 낮아야 할 것이다. 만약 위의 예시에서 성별이 여자로만 되어있다고 가정하면,
p(남)log(p(남))은 p(남)이 0이 될것이다.
.
아니? 로그에 0이 들어가면 음의 무한대 아닌가? : 맞다! 그렇기에 보통 아주 작은 값(0.05정도)을 더해서 처리하게 된다. (어차피 p(남) 때문에 0이 됨)
.
그렇다면 p(여)log(p(여))는 로그값때문에 0이 될 것이다. log(1)은 0이니까

엔트로피는 당연하게도 분기이전보다 이후에 더 낮아져야 한다. 그렇다면 이제는 정도의 문제이다. 엔트로피의 개념을 생각해보면, 엔트로피가 아주 크다가 분기 이후 아주 작아진다면 잘 분류가 되었다고 볼 수 있다.(서로 다른 것들을 최대한 분리시켰으니)

이렇게 부모노드의 엔트로피와 자식노드두개의 엔트로피 가중평균을 빼어 차이를 계산한 것이 정보이득이다. 이 정보이득이 큰 특성이 분기의 기준 특성으로 선택될 것이다.

특성 선택기준으로는 엔트로피가 아닌 지니불순도또한 존재한다.

decisonTree에서는 모든 특성에 대해서 특성선택 기준을 위한 불순도 계산을 진행하여 특성을 선택한다

엔트로피 계산식에서의 로그 와 마이너스

로그의 밑은 무엇으로 하는가의 질문까지 도달 가능하다. 일반적으로는 2를 사용한다. 이유는 정보 이론에서 정보량을 측정할 때, 이진 로그(binary logarithm)를 사용하기 때문이다. 이진 로그는 정보를 전달하기 위해 필요한 비트 수를 나타내기 때문에, 정보 이론에서 자주 사용된다. 따라서 엔트로피 계산식에서도 로그의 밑으로 2를 사용하는 것이 일반적이다.
엔트로피식에서의 로그값은 정보량이다. 동전의 앞면일 경우에 대한 정보량은 주사위를 던졌을 때 6일 경우에 대한 정보량보다 적다. 즉 정보량은 가능한 경우의 수가 더 많다는 것을 의미한다. 즉 낮은 확률을 보이는 사건에 대해서 로그(1/사건확률)은 큰 값을 가진다. 정보량이 크다는 뜻으로, 정보량이 크다는 것은 안보이는 무언가가 많다는 것으로 해석하면 옳다. 그렇기에 확률과 반비례성을 가진다. 엔트로피를 구하기 위해 정보량과 확률을 곱하는 행위는 정보의 양을 구하기 위해서이다.(정보량 != 정보의 양) 엔트로피가 높다는 것은 즉 정보의 양이 많다는 것이다. 즉 구분할 점이 많다는 것이다.
마이너스가 붙은 이유는 로그 그래프를 생각하면 당연히 이해가 될 것이다. x가 0~1까지에 대한 y값이 마이너스 값으로 뜨기 때문이다.

특성 선택에 대한 관점

그렇다면 우리는 어떤 특성을 선택해야 할까? 만약 특성이 매우 많고 설명변수의 수가 굉장히 많다면, 정보이득을 모든 특성에 대해 계산하는 것은 매우 비용이 많이 들 것이다.

일반적으로 랜덤 포레스트(DecisonTree계열 알고리즘)에서는 이런 특성 선택을 무작위로 진행한다. RF(랜덤포레스트)란 기본적으로는 결정트리의 원리를 따른다. 과정은 다음과 같다.

RandomForest(RF)

랜덤 포레스트는 앙상블 학습의 일종으로, 여러 개의 결정 트리를 생성하여 그 결과를 종합하는 방법입니다. 랜덤 포레스트에서는 다음과 같은 과정으로 앙상블 학습이 이루어집니다.
1. 랜덤 포레스트를 구성할 결정 트리의 개수를 정한다.
2. 각각의 결정 트리가 학습할 데이터를 랜덤하게 추출한다. 이 때 중복 추출이 허용되며, 추출된 데이터를 부트스트랩 샘플(bootstrap sample)이라고 한다.
3. 추출된 부트스트랩 샘플 데이터를 이용하여 각각의 결정 트리를 학습한다. 이 때 각 노드에서 분할을 할 때, 전체 특성 중 일부 특성만을 무작위로 선택하여 사용한다.
4. 모든 결정 트리의 예측 결과를 종합하여 최종 예측 결과를 도출한다.(결과를 평균내기)
이러한 방식으로 랜덤 포레스트는 다수의 결정 트리가 독립적으로 학습하고 예측하는 것을 통해 과적합을 방지하고, 높은 예측 성능을 얻을 수 있다.

기준 특성을 어떤 값을 기준으로 분기할 것인지?

예시로 제시된 표에서 성별을 기준 특성으로 가정한다면 어떻게 분기시킬지는 명확하다. 남자와 여자만으로 구분된 카테고리이기 때문이다. 당연하게도 남자인 설명변수와 여자인 설명변수를 나누면 끝이다.

다만 키에 대한 정보이득을 계산해보고 싶다면, 우리는 키를 기준으로 설명변수들을 분할 해야한다. 이때 키는 연속적으로 분포되어있다. 180과 160만 있는 것이 아니라 여러 키가 존재한다. 이때 우리는 "170을 기준으로 위아래로" 같은 기준을 생성한다. 실제 알고리즘은 이를 어떤 방식으로 정하는가에 대한 물음이다.

그렇다면 키가 100cm부터 200cm까지 모두 있다면 100cm, 101cm, 102cm... 200cm까지 백가지 경우에 대해서 모두 정보이득을 계산한다면 그것은 엄청난 비용을 초래할 것이다. 그렇기에 결정트리에서는 후보군을 만든다.

결정 트리 알고리즘에서 후보군은 해당 특성의 모든 가능한 분할점이다. 이 분할점은 해당 특성의 값의 중간값 또는 분위수를 사용하여 결정될 수 있습니다. 예를 들어, 키라는 특성이 있다면, 175cm가 분할점이 될 수 있다. 이러한 분할점들 중에서 가장 정보이득이 큰 것을 선택하여 해당 특성의 분할점으로 선택한다.