동적계획법이란 ?
동적 계획법은 큰 문제를 작은 문제로 나누어 푸는 문제를 일컫는 말입니다.
다만, 동적계획이라는 이름과 달리 딱히 동적이지도 않고(정해진 결과를 향해서 재계산하기 때문), 프로그래밍보다는 문제풀이 방식에 가깝습니다.
즉, 이것은 알고리즘이라기보다, 문제해결법에 대한 총칭에 가깝습니다.
따라서 번역된 말도 계획'법'이라고 명명되어 있습니다.
분할정복과 차이점
네, 거의 비슷하지만 결정적인 차이점이 있습니다. 바로 작은 문제가 중복이 일어나는지 안일어나는지 입니다. 분할정복은 큰 문제를 해결하기 어려워 단지 작은 문제로 나누어 푸는 방법입니다. 특징은 작은 문제에서 반복이 일어나는 부분이 없다는 점입니다. 동적프로그래밍은 어떨까요? 네, 작은 부분문제들이 반복되는 것(답이 바뀌지 않음)을 이용해 풀어나가는 방법입니다. (*Memoization)
동적계획 방법
- 모든 작은 문제들은 한번만 풀어야 합니다. 따라서 정답을 구한 작은 문제를 어딘가에 메모해 놓습니다. 다시 그보다 큰 문제를 풀어나갈 때 똑같은 작은 문제가 나타나면 앞서 메모(*Memoization) 한 작은 문제의 결과값을 이용합니다.
*Memoization
동적프로그래밍에서는 작은 문제들이 반복되고 이 작은 문제들의 결과값이 항상 같습니다. 때문에 이점을 이용하여 한번 계산한 작은 문제를 저장해놓고 다시 사용을 합니다. 이것을 Memoization이라고 합니다.
피보나치를 예로 들겠습니다. 피보나치는 1,1,2,3,5,8 ...의 수을 이루게 됩니다. 즉, 다음수열= 이전 수열 + 두단계 전 수열의 합이라는 점화식을 갖는 순열입니다. 재귀 함수로 풀게되면 이보다도 훨씬 간단하게 풀 수 있지만 n이 증가함에 따라 호출되는 함수의 수가 기하급수 적으로 증가하기 때문에 일정 수 이상의 순열을 구하기가 어렵습니다.
요약> 동적계획법의 조건
1. 작은 문제들이 반복된다.
F(5)를 구하기 위해서는 F(4), F(3)이 필요합니다. 다시 F(4)를 구하기 위해서는 F(3),F(2)가 필요합니다. 이 경우를 살펴보면 F(5)에서도 F(3)이 필요하고 F(4)에서도 F(3)이 필요함을 알 수 있습니다. 즉, 작은 문제가 반복되는 구조입니다.
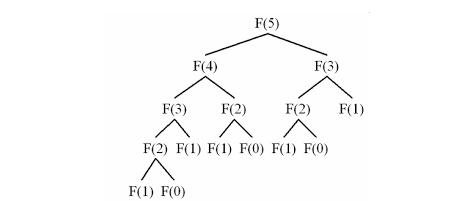
2. 같은 문제는 구할때 마다 정답이 같다.
Fibonacci 수열의 경우 첫번째 두번째 수열은 각각 1로 고정되어 있습니다.(편의상 0번째 항이 0이 되는 경우도 있습니다.) 즉, 3번째 수열은 언제나 결과가 2입니다. 또 4번째 수열은 3번째 수열과 2번째 수열을 이용해 구하므로 언제나 정답이 같다는 사실을 알 수 있습니다.
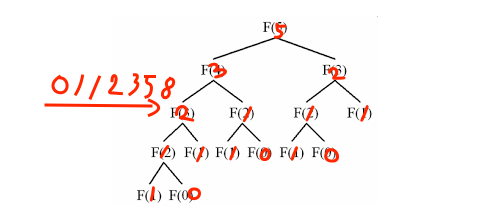
동적계획법에는 TopDown, BottomUp 두가지 방식으로 주로 풀이합니다.
TopDown은 위에서 아래로, 즉 문제풀이를 큰 수에서 작은 수로 내려오면서 확장합니다.
BottomUp은 아래에서 위로, 즉 문제풀이를 작은 수에서 큰 수로 올라가면서 확장합니다.
