정규분포(Normal Distribution)

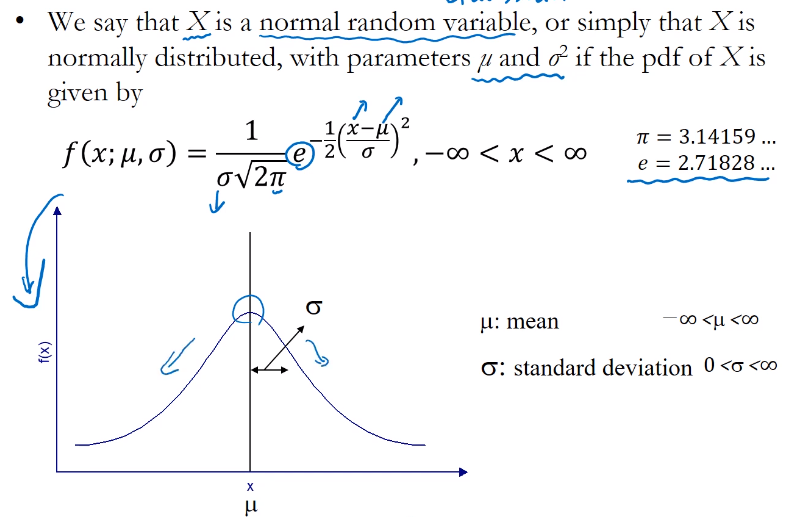
• Gaussian Distribution이라고 불리기도 한다.

정규분포의 특징

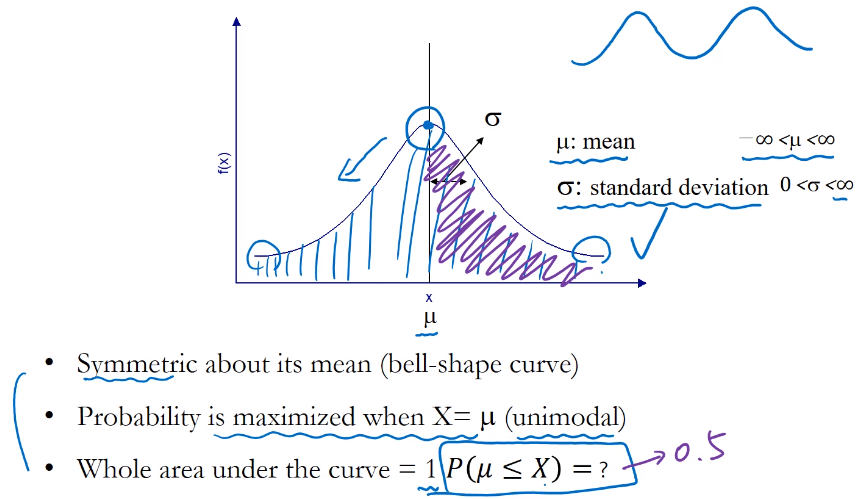
• 평균점에서 확률이 가장 높다.(Unimodal 봉우리가 하나있기 때문에)
• 평균을 기준으로 좌우 대칭이다.
• 곡선아래의 넓이 합은 1이다.
• Bell shaped curve라고도 불리운다.

Parameter에 따른 그래프 모양

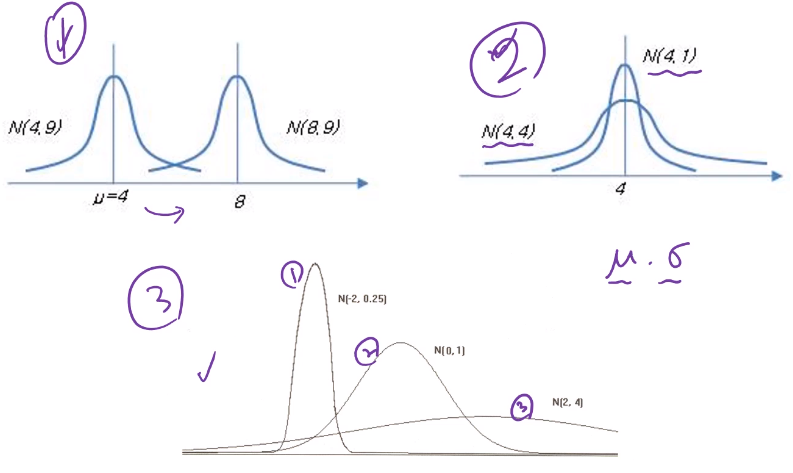
• 평균은 좌우로 위치가 달라지게 한다.
• 시그마는 그래프의 퍼짐 정도를 달라지게 한다.

기대값, 분산

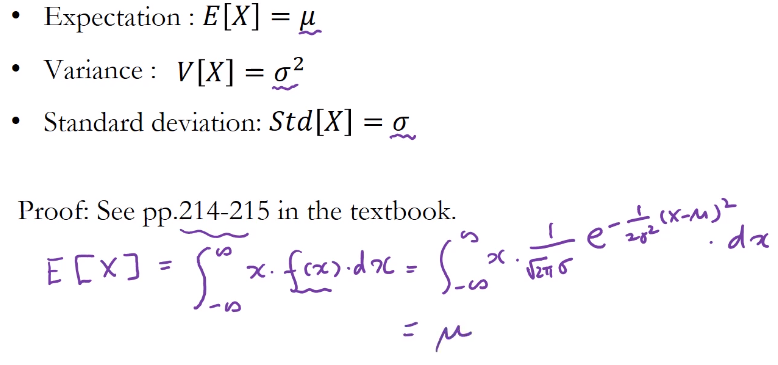
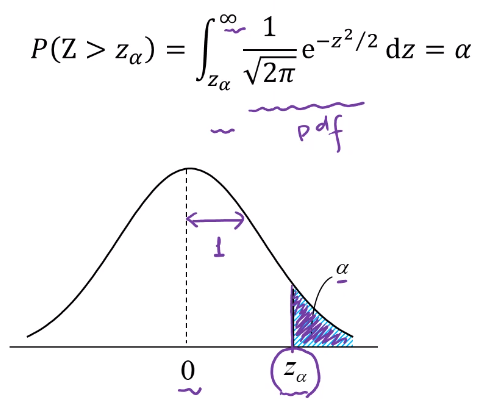
표준정규분포(Standard Normal Distribution)

• 평균이 0이고, 시그마가 1인 정규분포를 표준정규분포라 한다.
• 표준정규분포의 CDF를 phi of z라 한다.
• z가 표준정규확률변수 이다.
  

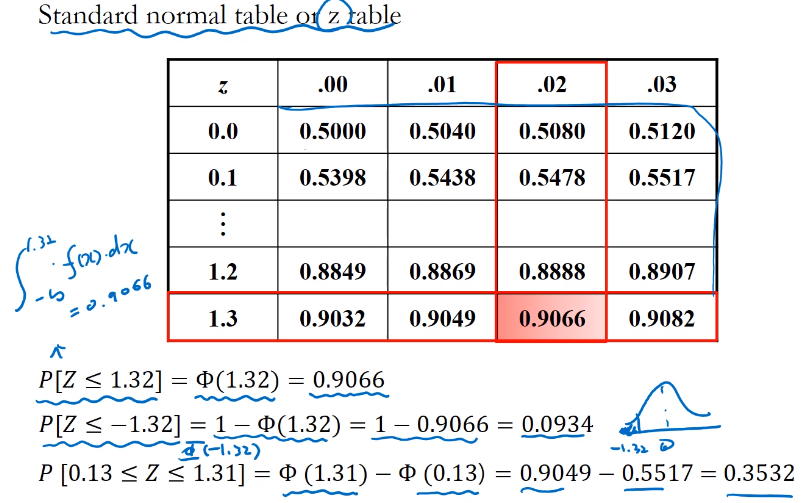
Z table(Standard Normal Table)

• 표준정규분포의 CDF에 대한 값들을 담는 표이다.
• 반복적인 적분계산이 tedious 하여서 만든 표.
  

표준정규분포를 활용한 정규분포의 확률 계산 방법

예제

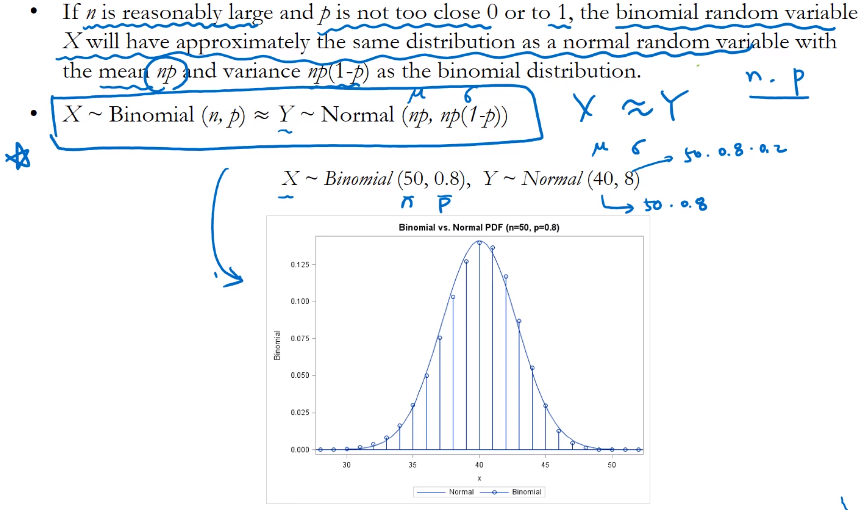
The Normal Approximation to the Binomial Distribution

• 정규분포와 이항분포의 분포가 비슷하여 이항분포에 대해 값을 계산할때 정규분포를 사용하여 대신 계산할수 있다.
• 이항분포에서 n이 크고, p가 1이나 0에 너무 가깝지 않을때 할수 있다.
• 평균은 np가 되고, 분산은 np(1-p)로 계산된다.
  

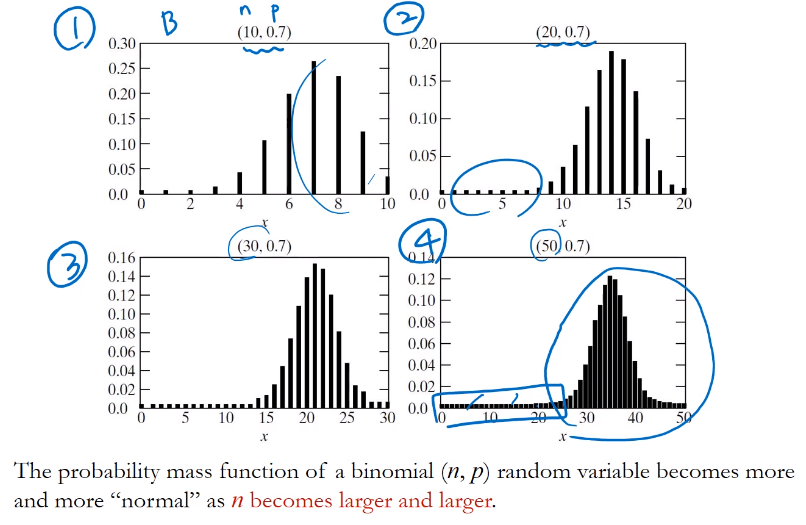
n이 커짐에 따른 근사화

근사 보정값

• 0.5를 더하거나 빼줌으로써 근사가 더 잘됨.
• 0.5라는 값은 경험적으로 알게된 값임.

예제