확률통계
1.1. Combinatorial Analysis
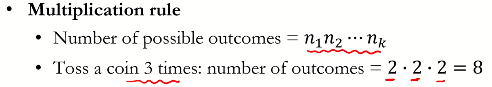
확률 통계에 대한 공부를 하는 이유지속적으로 나오는 확률론 및 통계에 대한 명확하지 않은 지식 체계화까먹은 내용 복습공부 진행 방법 \- 같이 공부하는 분과 노션통해 공부내용 공유 해당 공부내용의 일지는 개인 기록을 위해 작성공부자료: https://www
2.2. Axioms of Probability

Sample space(표본공간): 실험으로 부터 나온 모든 결과를 담고 있는 집합Experiment(실험): 데이터를 생성하는 모든 과정Event(사건, 이벤트): 표본공간의 부분 집합집합 E의 모든 원소가 집합 S의 원소이면 E는 S의 부분집합이다.Axiom(공리)
3.3. Conditional Probability and Independence-1
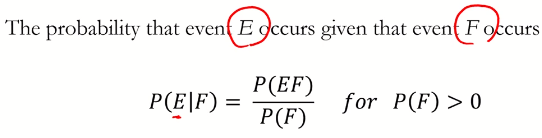
이벤트 E 와 F가 있을때, 이벤트 F가 일어났을때 이벤트 E가 일어날 확률확률 B에 대해서 구할때 A1, A2, A3가 상호배타일경우 확률 B에 대한 값은 조건부 확률의 합으로 구할수 있다.A given B에 대한 확률을 구했었다면 그 반대인 B given A는 위와
4.4. Conditional Probability and Independence-2

독립일경우 교집합 확률을 계산하기가 쉬워진다. 왜냐하면 조건부 부분이 사라지기 때문.
5.5. Random Variable
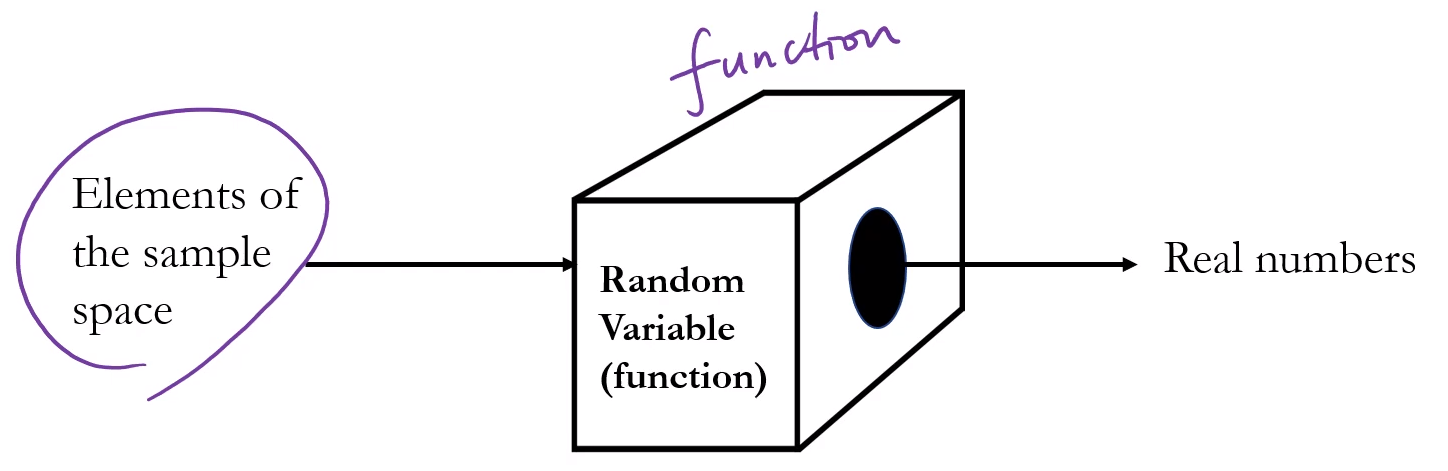
확률변수는 함수이다(중요)표본공간의 모든 원소를 실수로 대응하는 함수이와같이 표본공간의 원소가 실수로 대응되게 됨여기서는 헤드의 갯수를 기반으로셀수 있는 경우Continuous random variable(연속형 확률변수)셀수 없는 경우실수를 확률로 바꾸는 함수RV =
6.6. Expectation, Variance
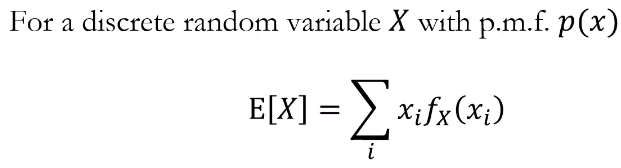
확률변수로부터 sample space의 샘플들이 실수로 주어졌을때(이산형, 연속형) 이런 많은 실수들을 요약하는 방법확률 변수에 대한 기댓값도 구할수 있지만, 확률변수의 함수에 대한 기댓값도 같은 방식으로 구할수 있다.
7.7. Probability Distributions, Bernoulli, Binomial
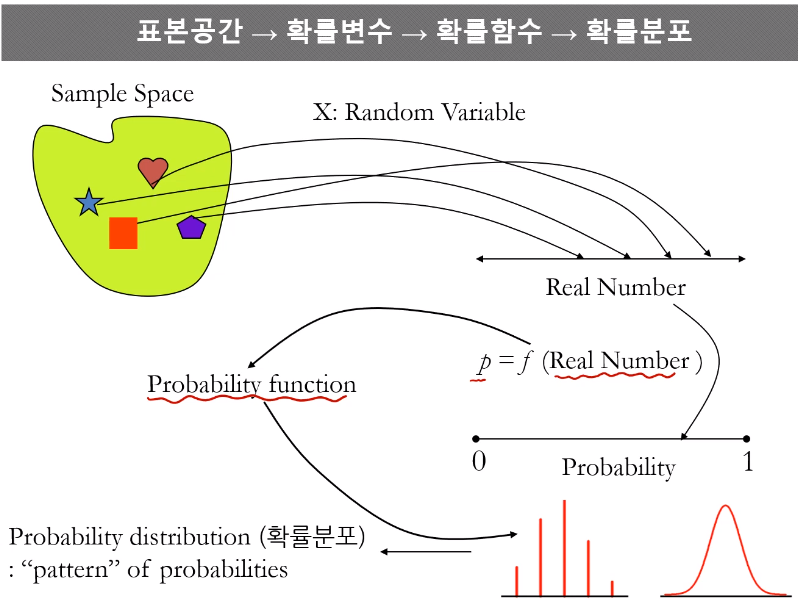
확률함수로부터 나온 확률들의 패턴확률질량함수 -> 이산형 확률분포확률밀도함수 -> 연속형 확률분포0과 1만 가질수 있다.0,1 로 나오는 베르누이 실험을 n번 반복했을때 성공이 나오는 횟수의 분포parameter(모수): 확률분포의 모양을 결정하는 매우 중요한 수. 모
8.8. Poisson Distribution

포아송 분포는 단위시간안에 특정 사건이 몇번 발생할 것인지를 표현 한다.포아송 분포의 parameter는 람다 하나이다.이항분포의 parameter n이 크고 p가 작게되면 포아송 분포로 근사할수 있다.
9.9. Geometric, Negative Binomial, Hypergeometric Distributions

Bernoulli trial(베르누이 실험) 에 기반한 분포Bernoulli trial은 0과 1의 값이 나오는 실험첫번째 성공이 일어날때까지 필요한 시행 횟수기하분포의 일반적인 버전이라 할수 있다.확률함수는 이항분포와 비슷하여 이런 이름을 지닌다.베르누이 시행에 기초
10.10. Continuous Random Variable

\[] 와 같은 대괄호는 포함을 뜻함() 는 포함하지 않음을 뜻함즉 (0,1) 0 ~ 1인데 0 과 1은 포함하지 않는 범위Probability Density Function(PDF)확률분포 곡선 아래에 있는 면적이 확률이 된다.PDF의 output은 항상 0보다 크거
11.11. Uniform Distribution

특정 구간내에 일정한 확률을 가지는 분포이외의 구간에서는 확률이 0전체 넓이가 1이 되어야 하기때문에 일양분포의 높이는 1/(B-a) 로 정해진다.
12.12. Normal Distribution
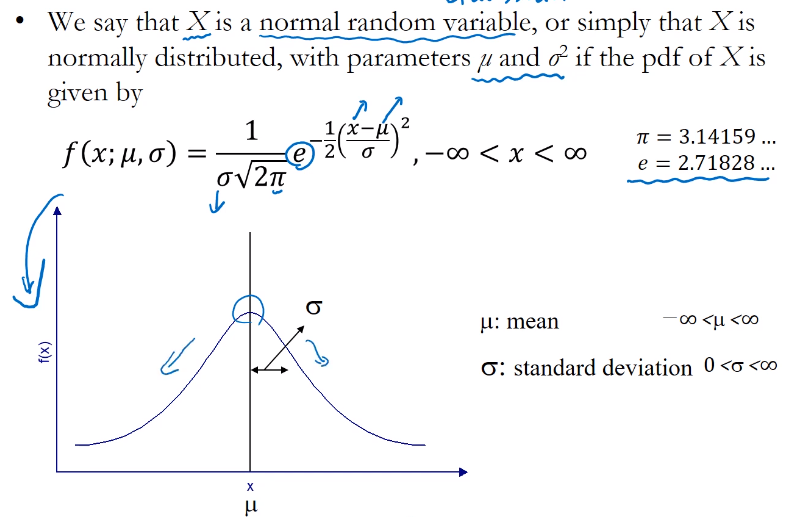
Gaussian Distribution이라고 불리기도 한다.평균점에서 확률이 가장 높다.(Unimodal 봉우리가 하나있기 때문에)평균을 기준으로 좌우 대칭이다.곡선아래의 넓이 합은 1이다.Bell shaped curve라고도 불리운다.평균은 좌우로 위치가 달라지게 한
13.13. Exponential Distribution

정규분포 다음으로 많이 쓰이는 연속형 확률분포이다.시간에 대해서 모델링된 분포이다.
14.14. Gamma, Beta Distribution

감마분포는 지수분포의 일반화된 형태이다.모수는 알파와 람다가 있다.알파는 shape parameter(형상모수)이다.람다는 rate(scale) parameter(척도모수)이다.알파가 1일때 지수분포와 동일해진다.비율에 대한 분포이다.모든 확률분포의 기대값과 분산은 p
15.15. Jointly Distributed Random Variables
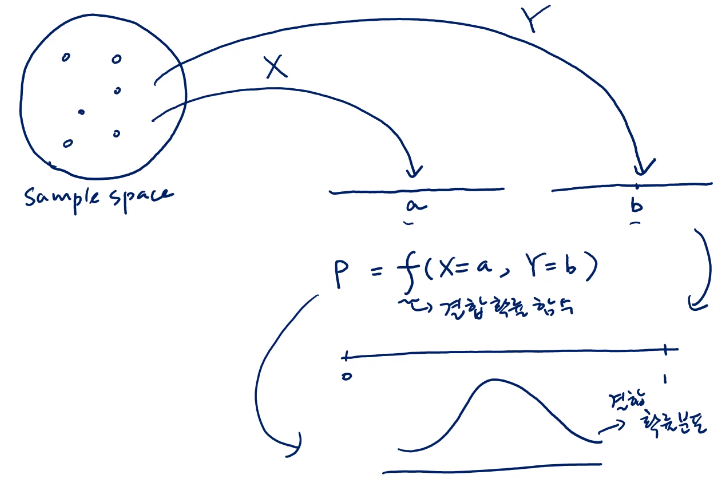
확률변수가 두개 이상일때, 두개의 확률변수를 동시에 고려하며 나타날 실수들의 확률이 결합확률이다.이러한 결합확률의 분포는 결합확률분포이다.PDF에서 변수가 2개이기 때문에 이중적분이 필요하다.먼저 x에 대해서 적분후 y에 대해서 하면 된다.
16.16. Jointly Distributed Random Variables 2(Marginal Probability, Independent Random Variable)
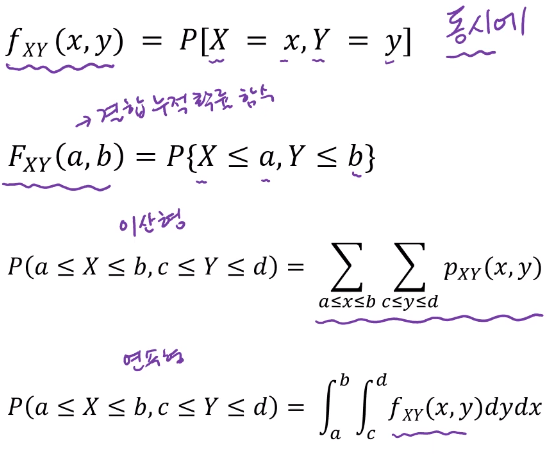
위와 같이 테이블로 표현 가능하다.결합확률이 각각의 확률의 곱과 같을때 확률변수가 서로 독립이라 한다.X, Y 가 서로 독립이라면 X의 값이 바뀌어도 Y의 분포에는 영향이 없다. 반대도 마찬가지다.서로 independent가 아닐때는 dependent라 한다.
17.17. Jointly Distributed Random Variables 3(Convolution)

Sums of Independent Random Variables 두개의 확률분포가 주어졌을때 서로가 독립이면 위와 같은 형태로 두 확률분포의 합에 대한 확률분포를 위와 같이 구할수 있다. 예제
18.18. Jointly Distributed Random Variable 4(Conditional probability)

결합이산확률분포에서 조건부확률 예제 결합연속확률분포에서 조건부확률 예제 X, Y가 독립일 경우 
X 와 Y 가 독립이면 공분산은 0이다.X 와 Y 의 공분산이 0이라도 서로 반드시 독립이라 할수 없다.