🔧변경내용🔨

제목	날짜	내용
발행일	23.03.15

📌들어가기에 앞서

해당 포스터는 자료구조 학습 내용 중 Tree Traversal 기초이론에 대한 내용을 정리한 것입니다.

특정 목적을 위해 트리의 모든 노드를 한 번씩 방문하는 것을 트리 순회라고 한다.

트리 구조는 계층적 구조라는 특별한 특징을 가진다.

모든 노드를 순회하는 방법엔 크게 세 가지가 있다.

트리를 순회할 수 있는 세 가지 방법은

1) 전위 순회

2) 중위 순회

3) 후위 순회

이 순회 방식들은 모두 노드를 순회할 때 왼쪽부터 오른쪽으로 조회한다는 공통점이 있다.

📖 전위 순회 (preorder traverse)

Root => Left => Right

• 전위 순회에서 가장 먼저 방문하는 노드는 루트

• 루트에서 시작해 왼쪽의 노드들을 순차적으로 둘러본 뒤, 왼쪽의 노드 탐색이 끝나면 오른쪽 노드를 탐색

• 즉 부모 노드가 제일 먼저 방문 되는 순회 방식

• 전위 순회는 주로 트리를 복사할 때 사용

---

📖 중위 순회 (inorder traverse)

Left => Root => Right

• 중위 순회는 루트를 가운데에 두고 순회

• 제일 왼쪽 끝에 있는 노드부터 순회하기 시작

• 루트를 기준으로 왼쪽에 있는 노드의 순회가 끝나면 루트를 거쳐 오른쪽에 있는 노드로 이동하여 마저 탐색

• 부모 노드가 서브 트리의 방문 중간에 방문되는 순회 방식

• 중위 순회는 이진 탐색 트리의 오름차순으로 값을 가져올 때 사용

---

📖 후위 순회 (postorder traverse)

Left => Right => Root

• 후위 순회는 루트를 가장 마지막에 순회

• 제일 왼쪽 끝에 있는 노드부터 순회하기 시작

• 루트를 거치지 않고 오른쪽으로 이동해 순회

• 제일 마지막에 루트를 방문

• 후위 순회는 트리를 삭제할 때 사용

  • 자식 노드가 먼저 삭제되어야 상위 노드를 삭제할 수 있기 때문

---

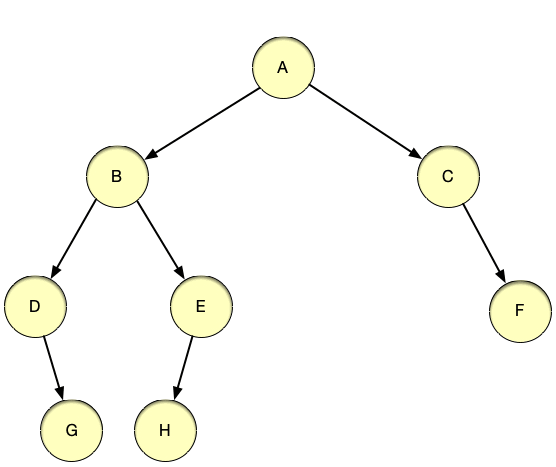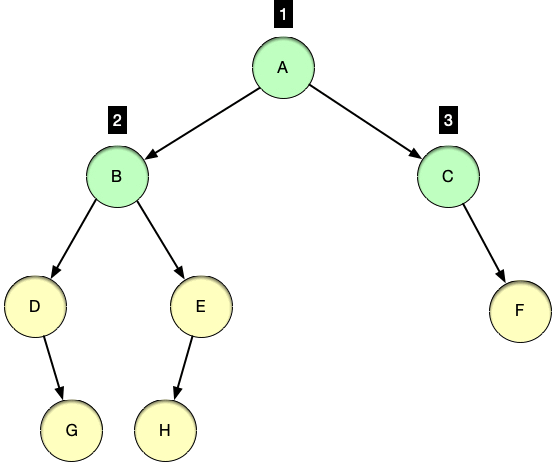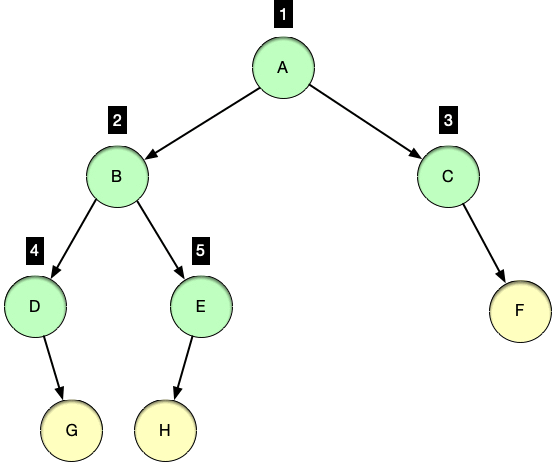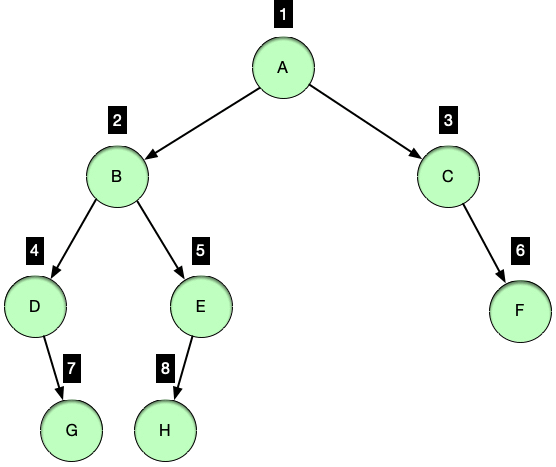
📖 레벨 순회 (levelorder traverse)

• 레벨 순회는 루트를 방문하는 기준으로 순회를 하는 것이 아닌 트리의 레벨 기준으로 노드들을 방문하는 순회 방법

• 루트 노드를 시작으로 아래로 뻗어나가며 노드들을 방문하며 루트 노드의 레벨이 1레벨이라고 했을 때 아래로 내려갈수록 레벨은 증가하는 특징을 보인다.

• 동일한 레벨에 여러 노드가 존재할 경우 왼쪽에서 오른쪽 순서로 노드를 방문

---

📖 순회 방식을 나누는 이유

• 이진 트리 탐색의 경우는 간단한 편이지만 순회 방법은 조금 복잡한 편

• 일정 조건에 의해 설계된 트리 구조는 자식 노드에 대한 조건이 명확하다면 원하는 값을 쉽게 찾아낼 수 있게 되지만,

  • 트리 구조 전체를 탐색할 때는 이야기가 조금 달라지기 때문

• 모든 노드를 방문하기 위해서는 일정한 조건이 필요하고,

  • 트리 구조를 유지보수하거나 특정 목적을 위해서도 순회 방법에 대한 정의는 필수적으로 필요

---

📚 레퍼런스

코드스테이츠 수업자료