Updated on 2024.02.04.
~ ING
Language: Python
참고 서적
I. 탐색 알고리즘
1-1 선형 탐색(Linear Search)
1) 개념
배열에서 원하는 값을 가진 원소를 찾을 때까지 순서대로 탐색하는 알고리즘이다.
시간 복잡도:
탐색 과정
| Index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Data | 1 | 2 | 3 | 4 | 5 |
- 찾고 싶은 값이 Data의 0번째 index의 값인지 비교
- 찾고 싶은 값과 Data의 index의 값이 같다면 검색 성공
찾고 싶은 값과 Data의 index의 값이 다르다면 index 값을 1 증가킨다. - Data의 끝에 도달할 때까지 2번을 반복하며, 끝에 도달하면 검색 실패이다.
2) 구현
def linearSearch(n):
for i in range(len(data)):
if data[i] == n:
return i
return -1
data = [1, 2, 3, 4, 5]
index = linearSearch(5)
if index == -1:
print("탐색 실패")
else:
print(index)1-2 이진 탐색(Binary Search)
1) 개념
정렬된 배열에서 탐색 범위를 반씩 줄여가면서 탐색하는 알고리즘이다.
시간 복잡도:
탐색 과정
| Index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Data | 1 | 2 | 3 | 4 | 5 |
- data의 중간값과 찾고자 하는 값을 비교한다.
- data의 중간값 == 찾고자 하는 값
- 탐색 성공
- data의 중간값 < 찾고자 하는 값
- 찾는 범위를 중간보다 한칸 뒤부터로 제한한다.
- data의 중간값 > 찾고자 하는 값
- 찾는 범위를 중간보다 한칸 앞까지로 제한한다.
- data의 중간값 == 찾고자 하는 값
- 찾는 범위가 사라지면 탐색 실패이고, 찾지 못했다면 1번으로 다시 돌아간다.
2) 구현
def binarySearch(start, end, n):
mid = (start+end) // 2
if start > end:
return -1
if data[mid] == n:
return mid
elif data[mid] > n:
return binarySearch(start, mid-1, n)
else:
return binarySearch(mid+1, end, n)
data = [1, 2, 3, 4, 5]
index = binarySearch(0, len(data), 4)
if index == -1:
print("탐색 실패")
else:
print(index)1-3 보간 탐색(Interpolation Search)
1) 개념
보간 탐색은 정렬된 배열에서 탐색 범위 내 값들의 분포를 고려한 보간식을 활용해, 이진 탐색보다 더 빠르게 검색할 수 있도록 설계된 알고리즘이다.
이진 탐색의 비효율성을 개선시킨 알고리즘.
시간복잡도:
이진 탐색은 값에 상관없이 탐색위치를 결정한다.
보간 탐색은 값이 상대적으로 앞에 위치한다고 판단하면, 앞쪽에서 탐색을 진행한다.
와 는 탐색대상의 시작과 끝에 해당하는 인덱스 값이고, 가 찾는 데이터의 인덱스 값이다. 보간 탐색은 데이터의 값과 그 데이터가 저장된 위치의 인덱스값이 비례한다고 가정한다.
따라서, 다음과 같은 비례식을 세울 수 있다.
이는 곳 s에 대한 식으로 다음과 같이 정리할 수 있다.
이진 탐색의 mid를 구하는 과정을 위의 과정을 활용하도록 변경하면 이진 탐색과 다른 점은 크게 없다.
2) 구현
def interpolationSearch(arr, first, last, target):
if arr[first] > target or arr[last] < target:
return -1
mid = int((target-arr[first]) / (arr[last]-arr[first]) * (last-first) + first)
print(mid)
if arr[mid] == target:
return mid
elif target < arr[mid]:
return interpolationSearch(arr, first, mid-1, target)
else:
return interpolationSearch(arr, mid+1, last, target)
ar = [1, 3, 5, 7, 9]
index = interpolationSearch(ar, 0, len(ar)-1, 8)
if index == -1:
print("탐색 실패")
else:
print(index)II. 정렬 알고리즘
| Sorting | Worst | Avg | Best | Run-time |
|---|---|---|---|---|
| 버블 정렬 | - | |||
| 선택 정렬 | - | |||
| 삽입 정렬 | - | |||
| 힙 정렬 | - | |||
| 병합 정렬 | - | |||
| 퀵 정렬 | - | |||
| 쉘 정렬 | - | |||
| 도수 정렬 | - | |||
| 기수 정렬 | - |
- 구현이 간단하지만 비효율적인 방법
- 버블 정렬
- 삽입 정렬
- 선택 정렬
- 구현이 복잡하지만 효율적인 방법
- 퀵 정렬
- 힙 정렬
- 병합 정렬
2-1 버블 정렬(Bubble Sort)
1) 개념
이웃한 두 원소의 대소 관계를 비교하여 필요에 따라 교환을 반복하는 알고리즘이다.
단순 교환 정렬이라고도 한다.
정렬 과정(오름차순)
| Index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Data | 2 | 4 | 3 | 5 | 1 |
- 0번째 index부터 배열의 끝까지 data[index]와 data[index+1]을 비교한다.
- data[index] > data[index+1]이면, data[index]와 data[index+1]을 swap
- 1회전시 정렬범위의 제일 오른쪽 원소는 제자리를 찾아간 것이므로, 오른쪽 정렬범위를 1씩 줄여가며 1번을 반복한다.
2) 구현
def bubbleSort():
for i in range(len(data)-1):
for j in range(len(data)-1-i):
if data[j] > data[j+1]:
(data[j], data[j+1]) = (data[j+1], data[j])
data = [2, 4, 3, 5, 1]
bubbleSort()
print(data)2-2 선택 정렬(Selection Sort)
1) 개념
선택 정렬은 리스트에서 최솟값(오름차순)을 찾아 앞쪽부터 차례로 교환하여 정렬하는 알고리즘이다.
오름차순인 경우, 배열의 정렬되지 않은 부분에서 가장 왼쪽 원소와 배열의 정렬되지 않은 부분에서 가장 작은 원소를 교환한다. 이 때, 교환된 가장 작은 원소는 정렬된 부분이 된다.
2) 구현
def selectionSort():
for i in range(len(data)):
minIndex = i
for j in range(i, len(data)):
if data[minIndex] > data[j]:
minIndex = j
data[i], data[minIndex] = (data[minIndex], data[i])
data = [2, 4, 3, 5, 1]
selectionSort()
print(data)2-3 삽입 정렬(Insertion Sort)
1) 개념
삽입 정렬은 리스트의 오른쪽부터 왼쪽으로 이동하며, 정렬되지 않은 요소를 정렬된 부분의 알맞은 위치에 삽입하는 방식으로 정렬하는 알고리즘이다.
2) 구현
def insertionSort():
for i in range(1, len(data)):
tmp = data[i]
j = i-1
while(True):
if j < 0:
break
if data[j] > tmp:
data[j+1] = data[j]
else:
break
j -= 1
data[j+1] = tmp
data = [2, 4, 3, 5, 1]
insertionSort()
print(data)
2-4 힙 정렬(Heap Sort)
1) 개념
힙 정렬은 배열을 힙 구조로 변환한 후, 루트 노드를 제거하고 힙을 재구성하는 과정을 반복해 정렬하는 알고리즘이다.
2) 구현
HEAP_LEN = 100
class Heap:
def __init__(self, numOfData = None, pc = None, heapList = None):
self.numOfData = numOfData
self.pc = pc
self.heapList = heapList
def HeapInit(self, pc):
self.numOfData = 0
self.comp = pc
self.heapList = [None for i in range(HEAP_LEN)]
def HisEmpty(self):
if self.numOfData == 0:
return True
else:
return False
def GetHiPriChildIDX(self, idx):
if GetLChildIDX(idx) > self.numOfData:
return False
elif GetLChildIDX(idx) == self.numOfData:
return GetLChildIDX(idx)
else:
if self.comp(self.heapList[GetLChildIDX(idx)], self.heapList[GetRChildIDX(idx)]) < 0:
return GetRChildIDX(idx)
else:
return GetLChildIDX(idx)
def HInsert(self, data):
idx = self.numOfData+1
while idx != 1:
if self.comp(data, self.heapList[GetParentIDX(idx)]) > 0:
self.heapList[idx] = self.heapList[GetParentIDX(idx)]
idx = GetParentIDX(idx)
else:
break
self.heapList[idx] = data
self.numOfData += 1
def HDelete(self):
retData = self.heapList[1]
lastElem = self.heapList[self.numOfData]
parentIdx = 1
while True:
childIdx = self.GetHiPriChildIDX(parentIdx)
if not childIdx:
break
if self.comp(lastElem, self.heapList[childIdx]) >= 0:
break
self.heapList[parentIdx] = self.heapList[childIdx]
parentIdx = childIdx
self.heapList[parentIdx] = lastElem
self.numOfData -= 1
return retData
def GetParentIDX(idx):
return idx//2
def GetLChildIDX(idx):
return idx*2
def GetRChildIDX(idx):
return GetLChildIDX(idx) + 1
# main
def DataPriorityComp(ch1, ch2):
return ch2-ch1 # minheap
# return ch1-ch2 # maxheap
data = [2, 4, 3, 5, 1]
heap = Heap()
heap.HeapInit(pc = DataPriorityComp)
for i in data:
heap.HInsert(i)
for i in range(len(data)):
data[i] = heap.HDelete()
print(data)2-5 병합 정렬(Merge Sort)
1) 개념
병합 정렬은 리스트를 재귀적으로 반으로 나누고, 나눠진 부분을 정렬한 후 합쳐서 최종적으로 정렬된 리스트를 만드는 알고리즘이다.
최선:
최악:
데이터 분포에 따른 영향이 없어서 항상 균일한 성능을 보장받을 수 있다.
하지만, 추가적인 메모리 공간이 필요하다.
2) 구현
① Python Style 구현
직관적인 구현이 가능하지만, 리스트 슬라이싱 시 리스트가 복제되기 때문에 메모리는 비효율적이다.
def merge_sort(data):
if len(data) <= 1:
return data
mid = len(data) // 2
left = data[:mid]
right = data[mid:]
left = merge_sort(left)
right = merge_sort(right)
return merge(left, right)
def merge(left, right):
result = []
i = 0
j = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result += left[i:]
result += right[j:]
return result
data = [2, 4, 3, 5, 1]
print(data)
print(merge_sort(data))2-6 퀵 정렬(Quick Sort)
1) 개념
퀵 정렬은 리스트에서 피벗(기준값)을 선택하고, 피벗보다 작은 값은 왼쪽, 큰 값은 오른쪽으로 배치한 후, 왼쪽과 오른쪽 부분을 재귀적으로 정렬하는 알고리즘이다.
2) 구현
def partition(arr, left, right):
pivot = arr[left]
low = left+1
high = right
while low <= high:
while low <= right and pivot >= arr[low] : # 경계를 벗어나지 않게 / pivot 보다 큰 값을 찾는 과정
low += 1
while high >= (left+1) and pivot <= arr[high] : # 경계를 벗어나지 않게 / pivot 보다 작은 값을 찾는 과정
high -= 1
if low <= high: # 교차되지 않으면 swap.
(arr[low], arr[high]) = (arr[high], arr[low])
(arr[left], arr[high]) = (arr[high], arr[left]) # pivot과 high 위치 교환.
return high # pivot의 위치 return
def quickSort(arr, left, right):
if left <= right:
pivot = partition(arr, left, right)
quickSort(arr, left, pivot-1)
quickSort(arr, pivot+1, right)
data = [2, 4, 3, 5, 1]
quickSort(data, 0, len(data)-1)
print(data)2-7 쉘 정렬(Shell Sort)
1) 개념
쉘 정렬은 간격을 두고 원소들을 비교하고 교환하는 방식으로 정렬을 진행하며, 간격을 점차 줄여가며 최종적으로 인접한 원소들을 정렬하는 알고리즘이다.
(수정)
2) 구현
def shellSort(a):
n = len(a)
h = n // 2
while h > 0:
for i in range(h, n):
j = i - h
tmp = a[i]
while j >= 0 and a[j] > tmp: # 교환하는 과정
a[j + h] = a[j]
j -= h
a[j + h] = tmp
'''
이는 선택 정렬의 형태가 된다. h만큼 계속 감소하면서 h만큼 더 감소한 만큼의
요소와 비교한다. 예를 들면, i가 8이고, h가 2이면, a[8]값을 tmp로 가지고
a[6]과 a[8]을 비교함을 시작으로 a[j] > a[i](tmp) 가 성립하지 않을 때까지 계속
a[4]와 a[6], a[2]와 a[4], ... 형태로 계속 비교하면서 더 큰 index에만 대입하며
아래까지 가서 a[8](tmp)를 넣어줌으로써 선택 정렬의 역할을 하도록 만든다.
'''
h //= 2
return a
data = [2, 4, 3, 5, 1]
print(data)
print(shellSort(data))
2-8 도수 정렬(Counting Sort)
1) 개념
도수 정렬은 입력된 데이터의 각 값이 나타난 횟수를 카운트하여, 그 정보를 바탕으로 정렬된 결과를 생성하는 알고리즘이다.
원소의 대소 관계를 판단하지 않고 빠르게 정렬하는 알고리즘
즉, if문을 사용하지 않고, for 문만 반복해서 정렬할 수 있는 알고리즘이다.
정렬 과정
Array (= a)
| Index | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Data | 2 | 4 | 3 | 5 | 1 |
1. 도수 분포표 만들기
'각 index에 해당하는 원소가 몇 개인지'를 나타내는 도수 분포표를 만든다.
Counting (= f)
| Index | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Data | 0 | 1 | 1 | 1 | 1 | 1 |
2. 누적 도수 분포표 만들기
'0번째 index부터 n까지의 원소가 몇 개 있는지'를 누적된 값을 나타내는 누적 도수 분포표를 만든다. counting 배열을 누적합으로 변환시킨다.
Counting (= f)
| Index | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Data | 0 | 1 | 2 | 3 | 4 | 5 |
여기서 알 수 있는 것은 ((counting 배열의 각 값) - 1)이 각 값의 뒤쪽부터 시작하는 index를 뜻한다.
즉, 1은 0번째 index부터 왼쪽으로 나올 수 있고, 2는 1번째 index부터 왼쪽으로 나올 수 있고, ..., 5는 4번째 index부터 왼쪽으로 나올 수 있다.
누적합의 목적은 큰 인덱스에 큰 값이 들어가도록 하여 결과 배열(작업용 배열)의 뒷쪽에 큰 값이 가도록 하기 위함이다.
즉, 누적 도수 분포표를 만듦으로써 각 원소가 몇번째 index에 위치하는지 알 수 있다.
3. 작업용 배열 만들기
이 부분은 글로 설명하는 것보다 코드를 보거나 그림을 보는게 더 직관적이다. (나는 이 정렬이 직관적이지 않아서 이해하기 힘들었다.)
- 배열의 끝에서부터 하나씩 본다.
- 배열의 각 값을 누적분포표의 index로 접근하여 1을 감소시킨다.
- 배열의 각 값을 누적분포표의 index로 접근한 값을 작업용 배열의 index에 배열의 값을 저장한다.
2번 과정이 올바른 index에 접근하기 위한 과정 + 중복된 값이 있을 때 반영해주기 위해서 -1씩 감소시키는 것이다.
3번 과정에서는 올바른 index에 접근하여 정렬하기 위한 값을 저장하는 과정이다.

for i in range(n-1, -1, -1):
f[a[i]] -= 1
b[f[a[i]] = a[i]- 최소값과 최대값을 미리 알고 있는 경우에만 적용할 수 있다.
- 작업용 배열을 만들 때 정렬하고자 하는 배열을 뒤에서 부터 스캔하는 것이 아닌 앞에서 부터 스캔했을 때 불안정 정렬이 된다. (같은 키 값의 순서 관계가 뒤바뀐다.)
- 새로운 배열(Counting)을 정의해야하는데, Array의 max와 min 값에 따라서 공간 복잡도가 높을 수 있다.
ex. 10개의 원소를 정렬하는데, min값이 1, max 값이 1억이면, 1억개의 공간을 만들어야한다.
2) 구현
def countingSort(a, max):
n = len(a) # 정렬할 배열 a
f = [0] * (max+1) # 누적 도수 분포표 배열 f
b = [0] * n # 작업용 배열 b
for i in range(n): # 도수 분포표
f[a[i]] += 1
for i in range(1, max+1): # 누적 도수 분포표
f[i] += f[i-1]
for i in range(n-1, -1, -1): # 작업용 배열 만들기
f[a[i]] -= 1
b[f[a[i]]] = a[i]
for i in range(n): # 배열 복사
a[i] = b[i]
data = [2, 4, 3, 5, 1]
print(data)
countingSort(data, max(data))
print(data)2-9 기수 정렬(Radix Sort)
1) 개념
기수 정렬은 각 자릿수를 기준으로 데이터를 정렬한 후, 자릿수를 차례로 올리며 정렬을 반복하는 알고리즘이다.
기수(Radix): 숫자의 자릿수.
O(n)
기수 정렬은 자리수 값에 따른 정렬.
[8, 2, 7, 3, 5] 리스트를 정렬한다고 할 때,
[[], [], [], [], [], [], [], [] ,[]] 이러한 형태로 버킷(bucket)을 구성해 자릿수를 담는 메로리 공간을 정의한다. 이는 각각 0~9 중 해당하는 값을 담을 수 있다. 따라서, 각 리스트 원소에 해당하는 인덱스에 넣어주는 것이다. 그러고 나서의 bucket은 다음의 형태가 된다.
[[], [], [2], [3], [], [5], [], [7], [8], []]
이후, 정렬 기준에 따라 순회하여 출력하면 될 것이다. 이 때, 추가적인 메모리 사용을 하지만, 비교 연산이 사용되지 않음이 핵심이다.
이것을 높은 자릿수로 확장할 때, 모든 숫자를 담으려고 하면 메모리 사용량이 매우 커지므로 자릿수만 담도록 확장하여 사용할 수 있다.
예를 들어, 10의 자릿수까지 담는다면 10개의 버킷으로 배분 과정을 2번 적용함으로써 정렬을 완료할 수 있다. 100의 자릿수만 10개의 버킷으로 3번이 될 것이다.
이의 과정을 간단히 설명하면, 제일 작은 자릿수부터 정렬을 하고, 점점 큰 자릿수로 정렬을 시킨다.
[28, 93, 39, 81, 52, 72, 38, 26]
[[], [81], [62, 72], [93], [], [], [26], [], [28, 38], [39]]
[81, 62, 72, 93, 26, 28, 38, 39]
[[], [], [26, 28], [38, 39], [], [], [62], [72], [81], [93]]
[26, 28, 38, 39, 62, 72, 81, 93]
이를 더 효율적으로 구현하고 싶다면, 버킷의 원소를 리스트 형태가 아닌 Queue로 구성하면 데이터가 많아져도 효율적으로 0번째 index를 뽑아낼 수 있을 것이다.
2) 구현
deque로 수정 필요
from queue import Queue
def radix_srot(a):
queues = []
for i in range(buckets):
queues.append(Queue())
n = len(a)
factor = 1
for d in range(digits):
for i in range(n):
queues[(a[i]//factor) % buckets].put(a[i])
j=0
for b in range(buckets):
while not queues[b].empty():
a[j] = queues[b].get()
j+=1
factor *= buckets
print(d+1, a)
buckets = 10
digits = 2
data = [28, 93, 39, 81, 52, 72, 38, 26]
print(data)
radix_srot(data)
print(data)III. 그래프 알고리즘
3-1 깊이우선탐색(Depth-First Search; DFS)
1) 개념
DFS은 그래프나 트리에서 시작 노드를 기준으로 가능한 깊은 곳까지 탐색한 후, 더 이상 탐색할 노드가 없으면 되돌아가면서 탐색을 이어가는 알고리즘이다.
2) 구현
① 인접 행렬 기반
def dfs(now):
print(now)
visited[now] = True
for next in range(1, v+1):
if not visited[next] and graph[now][next]:
dfs(next)
v = 10 # vertex
connection = [[1, 2], [1, 9], [2, 3], [3, 4], [3, 5], [7, 8]]
graph = [[0 for i in range(0, v+1)] for j in range(v+1)] # 인접 행렬 기반
visited = [False] * (v+1)
for start, end in connection:
graph[start][end] = 1
# graph[end][start] = 1 # undirected graph
dfs(1)② 인접 리스트 기반
def dfs(now):
print(now)
visited[now] = True
if not graph.get(now):
return
for next in graph.get(now):
if not visited[next]:
dfs(next)
v = 10 # vertex
connection = [[1, 2], [1, 9], [2, 3], [3, 4], [3, 5], [7, 8]]
graph = {} # 인접 리스트 기반
visited = [False] * (v+1)
for start, end in connection:
graph[start] = []
# graph[end] = [] # undirected graph
for start, end in connection:
graph[start].append(end)
# graph[end].append(start) # undirected graph
dfs(1)인접 리스트 기반으로 하면 dictionary를 쓰므로 불필요한 공간을 안만들어도 되는 장점이 있는 것 같다. 인접 행렬 기반으로 하면 n차 정방행렬을 만들어야 하므로 vertex가 1, 10, 100 이런 형식으로 구성되어 있다면 vertex가 3개임에도 불구하고 101차 정방행렬을 만들어야한다.
3-2 너비우선탐색(BFS, Breath-First Search)
1) 개념
BFS는 그래프나 트리에서 시작 노드부터 시작해, 인접한 노드를 먼저 방문한 후 다음 레벨의 노드들을 순차적으로 탐색하는 알고리즘이다.
2) 구현
① 인접 행렬 기반
from collections import deque
def bfs(queue):
while True:
if not queue:
break
now = queue.popleft()
print(now)
for next in range(1, v+1):
if not visited[next] and graph[now][next]:
queue.append(next)
visited[next] = True
v = 10 # vertex
connection = [[1, 2], [1, 9], [2, 3], [3, 4], [3, 5], [7, 8]]
graph = [[0 for i in range(v+1)] for j in range(v+1)] # 인접 리스트 기반
visited = [False] * (v+1)
queue = deque([])
for start, end in connection:
graph[start][end] = 1
# graph[end][start] = 1 # undirected graph
queue.append(1) # start point
visited[1] = True # start point
bfs(queue)② 인접 리스트 기반
from collections import deque
def bfs(queue):
while True:
if not queue:
break
now = queue.popleft()
print(now)
if not graph.get(now):
continue
for next in graph.get(now):
if not visited[next]:
queue.append(next)
visited[next] = True
v = 10 # vertex
connection = [[1, 2], [1, 9], [2, 3], [3, 4], [3, 5], [7, 8]]
graph = {} # 인접 리스트 기반
visited = [False] * (v+1)
queue = deque([])
for start, end in connection:
graph[start] = []
# graph[end] = [] # undirected graph
for start, end in connection:
graph[start].append(end)
# graph[end].append(start) # undirected graph
print(graph)
queue.append(1) # start point
visited[1] = True
bfs(queue)3-3 Floyd-Warshall 최단경로 알고리즘
1) 개념
그래프의 모든 쌍에 대해 최단 경로를 구하는 알고리즘으로, 각 노드 간의 직접적인 경로와 중간 노드를 고려하여 최단 경로를 반복적으로 업데이트한다.
, DP
예를 들어, A-C가 direct로 연결되어 있는데, A와 C는 각각 B와도 연결되어 있으면, A - B - C 이러한 경로를 고려할 수 있다. 이 때, A-C direct보다 A - B - C 경로가 더 cost가 적다면 A - C 경로를 A-B-C cost로 업데이트 한다. 이를 모든 정점을 돌면서 반복한다.
초기 테이블은 direct로 연결된 것만 표시하고, 나머지는 무한대로 둔다. 그러고 나서, 각 정점을 지나서 가는 것이 효율적이면 업데이트 한다.
2) 구현
def shortest_path_floyd(vertex, adj):
vsize = len(vertex)
a = list(adj)
for i in range(vsize): # 복사
a[i] = list(adj[i])
for k in range(vsize):
for i in range(vsize):
for j in range(vsize):
if (a[i][k] + a[k][j] < a[i][j]):
a[i][j] = a[i][k] + a[k][j]
printD(a)
def printD(D): # 현재의 최단거리 행렬 D를 화면에 출력하는 함수
vsize = len(D)
print("==============")
for i in range(vsize):
for j in range(vsize):
if D[i][j] == INF:
print("INF", end=' ')
else:
print("%d"%D[i][j], end=' ')
print()
INF = 9999
vertex = ['A', 'B', 'C', 'D', 'E', 'F', 'G' ]
weight = [ [0, 7, INF, INF, 3, 10, INF],
[7, 0, 4, 10, 2, 6, INF],
[INF, 4, 0, 2, INF, INF, INF],
[INF, 10, 2, 0, 11, 9, 4 ],
[3, 2, INF, 11, 0, 13, 5 ],
[10, 6, INF, 9, 13, 0, INF],
[INF, INF, INF, 4, 5, INF, 0 ]]
print("Shortest Path By Floyd's Algorithm")
shortest_path_floyd(vertex, weight)중첩문 세 개에다가 정의대로 구현할 수 있어서 직관적이고, 쉬운 알고리즘이다.
3-4 Dijkstra 최단경로 알고리즘
1) 개념
다익스트라 알고리즘은 그래프에서 한 정점에서 출발하여 다른 모든 정점까지의 최단경로 거리를 구하는 알고리즘으로, 시작 노드에서부터 인접한 노드들의 거리를 갱신하고, 방문한 노드를 제외한 노드 중 가장 짧은 경로를 가진 노드를 선택해 반복적으로 거리를 갱신해 나간다.
Greedy
집합 S에 포함되지 않은 정점 중 집합 S와 가장 가까운 정점을 선택한다. 최단거리가 확정된 정점들과 간선으로 직접 연결된 정점들 중에서 가장 가까운 정점을 선택한다.
집합 S에 새로운 정점이 들어오면 추가된 정점을 거쳐서 가는 새로운 경로가 기존의 경로보다 더 짧다면 모두 수정해야한다.
-
시작 정점과 나머지 정점 간의 직접적인 거리 관계를 정의하고 확정된 노드로 변경. 직접적으로 연결되어 있지 않으면 inf임.
-
확정되지 않은 정점 중 가장 거리가 낮은 순서, 거리가 같을 때는 정점의 숫자가 낮은 기준으로 확정되지 않은 정점과의 누적적, 직접적 거리 관계를 구하고, 더 작은 경우 업데이트 후 이 노드는 확정된 노드.

2) 구현
① 순차 탐색 기반 구현
def getMin():
min = 987654321
wheremin = -1
for now in T:
if not visited[now] and distance[now] < min:
min = distance[now]
wheremin = now
return wheremin
V, E = map(int, input().split())
myMap = [[0] * (V + 1) for _ in range(V + 1)]
for _ in range(E):
start, end, cost = map(int, input().split())
myMap[start][end] = cost
distance = [987654321] * (V + 1)
parent = [0] * (V + 1)
visited = [0] * (V + 1)
start = 0
distance[start] = 0
T = [i for i in range(V + 1) if i != start]
for i in range(V + 1):
if myMap[0][i]:
distance[i] = myMap[0][i]
for _ in range(V):
shortest = getMin()
visited[shortest] = True
# print(shortest)
for now in range(V+1):
if myMap[shortest][now] != 0 and distance[shortest] + myMap[shortest][now] < distance[now]:
distance[now] = distance[shortest] + myMap[shortest][now]
parent[now] = shortest
print(*distance)
print(*parent)
print("완성된 최단 거리:", *distance)
print("부모:", *parent)
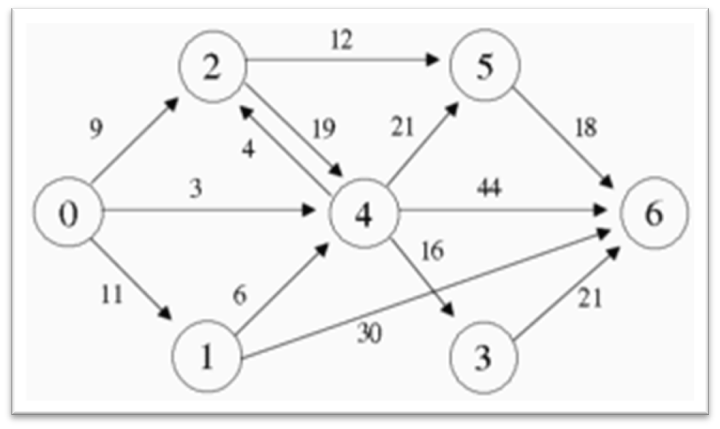
'''
input
7 13
0 1 11
0 2 9
0 4 3
1 4 6
1 6 30
2 4 19
2 5 12
3 6 21
4 2 4
4 3 16
4 5 21
4 6 44
5 6 18
'''② 우선순위 큐 기반 구현
순차 탐색에 비해 훨씬 효율적으로 사용할 수 있다.
import heapq
V, E = map(int, input().split())
myMap = [[] for _ in range(V + 1)]
for _ in range(E):
start, end, cost = map(int, input().split())
myMap[start].append((cost,end))
distance = [987654321] * (V + 1)
visited = [0] * (V + 1)
start = 0
distance[start] = 0
heap=[]
heapq.heappush(heap, (0,start))
while heap:
now_cost, now_node = heapq.heappop(heap)
if visited[now_node]:
continue
visited[now_node]=True
for next_cost, next_node in myMap[now_node]:
if distance[now_node]+next_cost < distance[next_node]:
distance[next_node]=distance[now_node]+next_cost
heapq.heappush(heap,(distance[next_node],next_node))
print("완성된 최단 거리", *distance)3-5 Union-Find Algorithm
1) 개념
원소끼리 집합을 만들고, 집합을 반환하는 알고리즘
서로소 부분집합이라고도 한다.
원소가 1, 2, 3, 4, 5, 6 인 집합일 때, 부분집합은 다음과 같다.
{1}, {2}, {3}, {4}, {5}, {6}
union(1, 4)와 union(5, 2)를 수행하면 다음과 같이 구성된다.
{1, 4}, {2, 5}, {3}, {6}
find는 대표 원소를 반환한다. 이 대표 원소는 트리로 구현하면 루트 노드를 뜻하며, 대체로 집합 내 가장 낮은 숫자를 의미한다.
2) 구현
def find(x):
if parent[x] != x:
parent[x] = find(parent[x])
return parent[x]
def union(a, b):
a = find(a)
b = find(b)
if a < b:
parent[b] = a
else:
parent[a] = b
parent = [i for i in range(v+1)]union(1, 2)
union(2, 3)
union(3, 4)
인 상태에서
find(4)를 하면 parent가 3인 상태
find(3)를 하면 parent가 2인 상태
find(2) -> parent 1
find(1) -> parent 1
1과 1이 동일하니, root 노드임을 알 수 있다. 이 값이 대표원소이다.
union은 a, b를 받으면 하나의 집합이 되는 것이므로 각각 대표원소를 찾고, 대표 원소 끼리의 대소비교를 해서 대표원소를 교체하게 된다.
3-6 Prim 알고리즘
1) 개념
최소비용 신장트리를 찾기 위한 알고리즘 중 하나로, 인접한 정점들 중에서 간선의 가중치가 가장 작은 정점을 선택해 트리를 확장해나간다.
greedy
- 신장트리(Spanning Tree)
- 연결 그래프 내의 모든 정점을 포함하는 트리.
- 사이클이 존재하지 않는다.
- 최소의 간선으로 연결 (vertex: v, edge: v-1)
- 최소비용 신장트리(Minimum Spanning Tree; MST)
: 가중치 그래프의 모든 신장트리 중에서 간선들의 가중치 합이 최소인 신장트리.
- 그래프 시작 정점 선택하여 초기 트리를 만든다.
- 현재 트리의 정점들과 인접한 정점들 중에서 간선의 가중치가 가장 작은 정점 v 선택
- v와 그 간선을 트리에 추가
- 모든 정점이 삽입될 때까지 2~3 반복.

2) 구현
def MSTPrim(vertex, adj):
vsize = len(vertex)
dist = [INF] * vsize
dist[0] = 0
selected = [False] * vsize
for i in range(vsize):
u = getMinVertex(dist, selected)
selected[u] = True
print(vertex[u], end=':')
for v in range(vsize):
if (adj[u][v] != None):
if selected[v] == False and adj[u][v] < dist[v]:
dist[v] = adj[u][v]
print(dist)
def getMinVertex(dist, selected):
minv = -1
mindist = INF
for v in range(len(dist)):
if not selected[v] and dist[v] < mindist:
mindist = dist[v]
minv = v
return minv
vertex = [ 'A', 'B', 'C', 'D', 'E', 'F', 'G' ]
weight = [ [ None, 29,None,None,None, 10,None ],
[ 29,None, 16,None,None,None, 15 ],
[ None, 16,None, 12,None,None,None ],
[ None,None, 12,None, 22,None, 18 ],
[ None,None,None, 22,None, 27, 25 ],
[ 10,None,None,None, 27,None,None ],
[ None, 15,None, 18, 25,None,None ]]
INF = 9999
print("MST By Prim's Algorithm")
MSTPrim(vertex, weight)3-7 Kruskal Algorithm
1) 개념
그래프에서 최소 신장 트리를 구하는 알고리즘 중 하나로, 모든 간선을 가중치 순으로 정렬한 뒤, 사이클을 형성하지 않는 선에서 가장 가중치가 작은 간선을 하나씩 선택해 트리를 확장해 나간다.
- 그래프의 모든 간선을 가중치에 따라 오름차순 정렬
- 가장 가중치가 작은 간선 e를 뽑는다.
- e를 신장트리에 넣었을 때 사이클이 생기면 넣지 않고, 2번으로 이동한다.
- 사이클이 생기지 않으면 최소 신장트리에 삽입한다.
- n-1개의 간선이 삽입될 때까지 2번으로 이동한다.

이 때, 사이클이 생성되는지 검사하기 위해서 서로소 부분 집합, Union-Find 알고리즘을 통해 사용된다.
2) 구현
def find(x):
if parent[x] != x:
parent[x] = find(parent[x])
return parent[x]
def union(a, b):
a = find(a)
b = find(b)
if a < b:
parent[b] = a
else:
parent[a] = b
v, e = map(int, input().split())
myMap = []
parent = [i for i in range(v+1)]
result = 0
for _ in range(e):
a, b, cost = map(int, input().split())
myMap.append((cost, a, b))
print(myMap)
# kruskal
myMap.sort()
print(myMap)
for edge in myMap:
cost, a, b = edge
if find(a) != find(b):
union(a, b)
result += cost
print(a, b, parent)
print(result)전체 그래프에서 가장 작은 값들부터 찾기 위해 cost 기준으로 sort한다. 그리고, 그 작은 값들 부터 순회하면서 find(a) != find(b) 조건을 통해 같은 집합인지 확인한다. 이 방식으로 간선을 연결했을 때 사이클인지 아닌지 확인하고 있다. 사이클이 아니라면 union으로 같은 집합으로 만들면서 cost만큼 결과값을 증가시킨다.
IV. 문자열 알고리즘
4-1 브루트 포스(Brute Force)
1) 개념
패턴을 텍스트의 처음부터 끝까지 하나씩 비교하며 찾는 간단한 알고리즘이다.
선형 탐색을 확장시킨 알고리즘.
단순법이라고도 부른다.
탐색 과정
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Text | A | B | A | B | C | D | E | F | G | H |
| Pattern | A | B | C |
- Text의 첫번째 문자부터 Pattern 과 일치하는지 검사.
- 해당 부분과 Pattern이 같지않으면 Pattern을 오른쪽으로 한 칸민다.
- Pattern이 일치할 때까지 2번을 반복한다.
일치하는지 검사하는 것은 순차탐색과 같이 한 문자 한 문자 비교한다.
2) 구현
def BruteForce(text, pattern):
ptext = 0
pptn = 0
while True:
# text를 가리키는 index가 text의 크기를 넘어서지 않게, 패턴을 가리키는 index가 패턴의 크기를 넘어서지 않게.
# 패턴의 경우 패턴이 모두 text 내에 존재하면 패턴을 가리키는 index가 패턴의 크기가 되므로 종료조건 명시.
if ptext == len(text) or pptn == len(pattern):
break
# 패턴의 첫머리가 text의 한 부분과 같을 때 계속 증가하며 패턴이 모두 존재하는지 확인.
if text[ptext] == pattern[pptn]:
ptext += 1
pptn += 1
else:
# 패턴의 일정 크기만큼 봤는데, 패턴이 존재하지 않을 때 다시 순서대로 텍스트를 볼 수 있도록 줄이는 과정
ptext = ptext-pptn + 1
# 패턴의 첫머리가 text의 일정 부분과 맞지 않으니 text의 다른 부분에 당연히 패턴의 0번째부터 확인하기 위함.
pptn = 0
if pptn == len(pattern): # 패턴이 text 내에 존재하면 패턴을 모두 확인한 것이므로 pptn이 패턴의 길이가 됨.
# 텍스트 내의 패턴의 끝 index에서 패턴의 크기만큼 빼줌으로써
# 텍스트에서 나타나는 패턴의 첫번째 index를 return 해줄 수 있음.
return ptext-pptn
else:
return -1
text = "ABABCDEFGHA"
pattern = "ABC"
idx = BruteForce(text, pattern)
if idx == -1:
print("텍스트 안에 패턴이 존재하지 않음")
else:
print("%d번째에 패턴 존재" %(idx+1))위 구현보다 아래의 구현이 이해하기 조금 더 쉬운 것 같다.
def string_matching(T, P):
n = len(T)
m = len(P)
for i in range(n-m+1):
j=0
while j<m and P[j] == T[i+j]:
j+=1
if j == m:
return i
return -1
text = "HELLO WORLD"
pattern = "LO"
print(pattern, 'in', text, '-->', string_matching(text, pattern))
pattern = "HI"
print(pattern, 'in', text, '-->', string_matching(text, pattern))총 text의 길이까지 본다. 패턴 갯수를 넘지 않고, 패턴에서의 글자와 text에서의 글자가 맞으면 다음 index를 비교. index가 패턴 길이까지 오면 찾은 것.
4-2 KMP 법
1) 개념
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Text | Z | A | B | C | A | B | X | A | C | C | A | D | E | F |
| Pattern | A | B | C | A | B | D |
2) 구현
4-3 보이어 · 무어법
1) 개념
최선:
평균:
최악:
2) 구현
4-4 보이어무어 호스풀 알고리즘(Boyer-Moore-Horspool Algorithm)
1) 개념
최선:
평균:
최악:
보이어 무어의 단순한 형태.
휴리스틱을 이용하여 효율적 문자열 매칭 알고리즘.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Text | A | P | P | L | E | M | A | N | G | O | B | A | N | A | N | A | ... |
| Pattern | B | A | N | A | N | A |
패턴의 가장 뒤 인덱스부터 앞으로 오면서 비교하는 형태이다. 이때, 패턴과 불일치가 발생하면 생성한 시프트 테이블를 가지고 효율적으로 탐색할 수 있다.
사프트 테이블(Shift Table)
크기는 사용될 수 있는 전체 문자의 갯수이다. 아스키 코드라고 한다면 128개가 될 것이다.
불일치 문자가 패턴 내에 미존재할 경우 패턴의 크기(m)만큼 움직이기 때문에 시프트 테이블의 기본값은 모두 패턴의 길이로 지정한다.
ex.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Text | A | P | P | L | E | M | A | N | G | O | B | A | N | A | N | A | ... |
| Pattern | B | A | N | A | N | A |
불일치 문자가 패턴 내에 존재할 경우, 패턴의 가장 문자로부터 처음으로 일치하는 index와 패턴을 맞춰서 다시 한번 확인해보는 과정이 필요하기 때문에 그 값을 (패턴의 크기 - 1 - 해당 문자가 패턴의 우측으로부터 처음으로 나오는 번째수)로 바꿔준다.
ex.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Text | A | P | P | L | E | M | A | N | G | O | B | A | N | A | N | A | ... |
| Pattern | B | A | N | A | N | A |
따라서, 시프트 테이블은 아래의 형태가 될 것이다.
| Index | 0 | ... | 65 | 66 | ... | 78 | ... | 127 |
|---|---|---|---|---|---|---|---|---|
| ASCII | NUL | ... | A | B | ... | N | ... | DEL |
| 이동거리 | 6 | ... | 2 | 5 | ... | 1 | ... | 6 |
패턴과 불일치하는 문자를 만났을 때 시프트 테이블을 바로 참조해서 그 만큼 이동해서 다시 비교해주는 것을 반복하여 수행한다.
2) 구현
아스키 코드의 대문자 부분만 가지고 구현한 호스풀 알고리즘.
NO_OF_CHARS = 26
def shift_table(pat):
m = len(pat)
tbl = [m] * NO_OF_CHARS
for i in range(m-1):
index = ord(pat[i])- ord('A')
tbl[index] = m-1-i
return tbl
def search_horspool(T, P):
m = len(P)
n = len(T)
t = shift_table(P)
i = m-1
while(i <= n-1):
k = 0 # 매칭 문자수
while k<= m-1 and P[m-1-k] == T[i-k]:
k += 1
if k==m:
return i-m+1 # 모두 일치하면 패턴의 가장 끝 위치를 가리키므로 패턴 길이만큼 빼주고, index -> length이므로 +1 해주면 가장 처음의 위치 반환
else:
i += t[ord(T[i]) - ord('A')]
return -1
print(shift_table("BANANA"))
print("패턴의 위치:", search_horspool("APPLEMANGOBANANAGRAPE", "BANANA"))V. 수학 알고리즘
5-1 최대공약수(Greatest Common Divisor; GCD) & 최소공배수(Least Common Multiple; LCM)
1) 유클리드 호제법(Euclidean Algorithm)
a > b일때 a, b의 최대공약수(GCD)를 구하는 알고리즘.
이므로, 유클리드 호제법으로 GCD를 구하고, LCM을 구하면 빠르게 구할 수 있다.
def gcd(a, b):
while b != 0:
r = a%b
a = b
b = r
return a
def lcm(a, b):
return a*b // gcd(a, b)
print(gcd(60, 28))
print(lcm(60, 28))5-2 거듭 제곱
1) 분할 정복(Divide and Conquer) 기반 구현
power는 9번 호출하고, 각 호출마다 곱셈이 이루어져 9번 + 홀수일때 추가적인 곱셈이 발생하므로 5번 = 14번 곱셈이 이루어진다.
def power(x, n): # 축소 정복 기법
if n==0:
return 1.0
elif n%2 == 0:
return power(x*x, n//2)
else:
return x*power(x*x, (n-1)//2)
print(power(2, 500))5-3 k번째 작은 수
정렬되지 않은 배열에서 k번째 작은 수를 빠르게 찾는 알고리즘으로, quick sort 과정 중 pivot은 각 iteration 마다 제자리를 찾게 되는 과정에서 pivot이 k 자리에 들어가 제자리를 찾게 되면 중간에 중단하는 알고리즘이다.
def partition(a, left, right):
low = left+1
high = right
pivot = a[left]
while low <= high:
while low<=right and a[low] <= pivot:
low+=1
while high>=left and a[high] > pivot:
high-=1
if low < high:
a[low], a[high] = a[high], a[low]
a[left], a[high] = a[high], a[left] # pivot <-> high
return high
def quick_select(a, left, right, k):
pos = partition(a, left, right)
if pos+1 == left+k:
return a[pos]
elif pos+1 > left+k:
return quick_select(a, left, pos-1, k)
else:
return quick_select(a, pos+1, right, k-(pos+1-left))
array = [12, 3, 5, 7, 4, 19, 26, 23, 15]
print("입력 리스트 =", array)
print("3번재 작은 수: ", quick_select(array, 0, len(array)-1, 3))5-4 에라토스테네스의 체
1~n까지의 소수를 효율적인 방법으로 탐색하는 알고리즘이다.
에라토스테네스의 체의 과정 (n = 36)
- 1 ~ 36까지의 모든 수를 적는다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 - 소수도, 합성수도 아닌 1을 제거한다.
- 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 - 2를 제외한 2의 배수 제거
- 2 3 - 5 - 7 - 9 - 11 - 13 - 15 - 17 - 19 - 21 - 23 - 25 - 27 - 29 - 31 - 33 - 35 - - 3을 제외한 3의 배수 제거
- 2 3 - 5 - 7 - - - 11 - 13 - - - 17 - 19 - - - 23 - 25 - - - 29 - 31 - - - 35 - - 5를 제외한 5의 배수 제거
- 2 3 - 5 - 7 - - - 11 - 13 - - - 17 - 19 - - - 23 - - - - - 29 - 31 - - - - - - 종료.
즉, 일반화하면 다음의 과정과 같다.
- 2~n까지의 모든 수를 적는다.
- 남은 수의 순서대로 자기자신을 제외한 자신의 배수를 제거한다.
- 2번을 이를 n의 제곱근까지 수행한다.
왜 제곱근까지 수행하는가? n까지 수행해야하는 것이 아닌가?
36은 두 수의 곱으로 나타낼 수 있다.
a * b = 36
여기서 a, b는 다음의 숫자쌍을 가질 수 있다.
(1, 36), (2, 18), (3, 12), (4, 9), (6, 6), (9, 4), (12, 3), (18, 2), (36, 1)
어떠한 수든 두 수의 곱의 순서쌍을 나타내면 제곱근을 기준으로 대칭을 이룬다. 즉, 에라토스테네스의 체에서는 n까지만 볼 것이므로 n의 제곱근을 넘어서면 이미 제거된 수가 된다.
수식으로 설명하자면, 일때만 확인하면 그 이후의 a, b는 이미 제거된 수가 된다.
기존 소수를 구하려면 의 시간복잡도가 걸리는데, 이 방식은 의 시간복잡도가 걸려 매우 효율적인 처리가 가능하다.
다른 자료들을 찾아보면 직관적이지 않아서 처음에 이해하기가 힘든데, 나는 조금 더 Python-Style로, 직관적으로 구현해봤다.
import math
n = 100
arr = [True] * (n+1)
# 소수 판별
for i in range(2, int(math.sqrt(n))+1):
if arr[i]:
for j in range(2*i, n+1, i):
arr[j] = False
# 소수 출력
for i in range(2, n+1):
if arr[i]:
print(i, end=' ')VI. 비트마스크(Bitmask) 알고리즘
6-1 Poisoned Wine
왕이 N병의 와인을 가지고 있다. 그 중 1병에만 독이 들어 있다. 왕은 자신의 신하들을 사용해 어떤 병에 독이 있는지 알아내려고 한다. 독이 든 와인을 마시면 죽지만, 독은 시간이 지나야 효과가 나타난다. 왕은 최대한 적은 수의 신하를 사용하여 독이 든 와인을 찾아내고 싶다. 한 번만에 찾고 싶기 때문에 한 번에 여러 병을 신하들에게 주고 관찰한 후에 독이 든 병을 찾아야 한다.
즉, 최소한의 신하들을 사용하여 한 번의 실험으로 독이 든 와인병을 찾아야한다.
일반적으로 신하 n명에게 각 1개 통씩 먹여야 한다. 하지만 다음의 과정을 통해 신하수를 줄일 수 있다.
| 10진수 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2진수 | 1010 | 1001 | 1000 | 0111 | 0110 | 0101 | 0100 | 0011 | 0010 | 0001 | 0000 |
위처럼 통마다 0부터 순서대로 번호를 매겨 10진수에서 2진수로 변환하고, 각 변환된 수의 1이 들어있는 위치를 신하의 순서대로 음용한다. 예를 들어, 총 통이 10개가 있다고 가정하면, 10번 통은 4번째 신하와 2번째 신하가 마셔보고, 6번 통은 3번 신하와 2번 신하가 마셔본다. 이 방식으로 원래 n개의 통이 있으면 n명의 신하가 필요한 것을 명으로 줄일 수 있다.
VII. 알고리즘 설계 기법 (algorithm design paradigms)
7-1 분할정복 기법(Divide and Conquer)
분할 정복 기법은 문제를 더 작은 하위 문제로 나눈 후, 각 하위 문제를 해결하고 그 결과를 합쳐 최종 문제를 해결하는 알고리즘 기법이다.
대표 문제
- Binary Search
- Interpolation Search
- Insertion Search
- Merge Sort
- Quick Sort
- Quick Select Algorithm
- Fake Coin Problem
- Closest Pair of Points
- Strassen's Algorithm
7-2 탐욕적 기법 (Greedy Method)
각 순간에 최적이라고 생각되는 해를 선택하는 방법.
근시안적 알고리즘이라고도 부른다.
시간적으로는 다른 기법보다는 효율적이나, 궁극적인 최적해를 보장하지 않는다.
그리디로 항상 최적해를 구할 수 있거나, 다른 기법으로 최적해를 구하는 것이 현실적으로 불가할 때 사용할 수 있다.
대표 문제
- Coin Change Problem
- Fractional Knapsack
- Prim Algorithm
- Kruskal Algorithm
- Dijkstra Algorithm
- Huffman Code
1) Fractional Knapsack
0-1 Knapsack은 어떤 탐욕을 사용해도 최적해를 만들 수 없다. 완전 탐색을 하던지, 무게를 정수로 제한하고 DP 쓰는 것이 최적해를 구하는 방법이다. 기존의 Knapsack 문제를 물건을 분할해서 일부만 넣을 수 있다면 greedy로 최적해를 구할 수 있다.
단위 무게당 가격인 높은 물건부터 배낭의 용량이 넘지 않을 때까지 넣으면 성립한다.
def knapSack_factional_greedy(obj, capacity):
obj.sort(key=lambda item: item[2] / item[1], reverse=True) # value 기준 정렬
total_value = 0
for _, weight, value in obj:
if capacity == 0:
break
if capacity >= weight:
capacity -= weight
total_value += value
else:
fraction = capacity / weight
total_value += (value * fraction)
capacity = 0
return total_value
obj = [("A", 10, 80), ('B', 12, 120), ('C', 8, 60)]
print("W=18", obj)
print("부분적 배낭(18):", knapSack_factional_greedy(obj, 18), end='\n\n')
obj = [("A", 10, 60), ('B', 40, 40), ('C', 20, 100), ('D', 30, 120)]
print("W=50", obj)
print("부분적 배낭(50):", knapSack_factional_greedy(obj, 50), end='\n\n')7-3 DP (Dynamic Programming)
동적 계획법(DP)은 복잡한 문제를 더 작은 하위 문제로 나누어 해결하고, 그 결과를 저장하여 동일한 문제를 반복적으로 계산하지 않도록 최적화하는 알고리즘 기법이다.
대표 문제
- Binomial Coefficient
- 0-1 Knapsack
- LCS
- Edit Distance
- Floyd-Warshall Algorithm
- Fibonacci Sequence
피보나치 수열의 DP <이미지 추가>
1) 메모이제이션(Memoization)을 이용한 피보나치
값을 Memo 하면서 연산한다고 보면 될 것 같다.
이 경우도 Top-Down을 사용하지만, 각 단계에서 이미 풀린 문제인지 확인하고, 풀린 문제이면 저장된 값을 이용하고, 풀리지 않은 문제이면 풀고 값을 저장한다.
의 시간복잡도.
2) 테이블화(Tabulation)를 이용한 피보나치 수열 (Bottom-up)
메모이제이션과 비슷하지만, 순차적으로 채워나간다는 것에 초점을 둔다. 기반 사항에 대한 항목을 채우고, 이를 바탕으로 상위 테이블을 채워나가는 형식이다. 반복문으로 구현한 피보나치라고 생각하면 편하다.
4) 구현
def fib(n): # Divide and Conquer
if n==0:
return 0
elif n==1:
return 1
else:
return fib(n-1) + fib(n-2)
def fib_dp_tab(n): # tabulation
f = [None]*(n+1)
f[0] = 0
f[1] = 1
for i in range(2, n+1):
f[i] = f[i-1] + f[i-2]
return f[n]
def fib_dp_mem(n): # memoizaiton
if (mem[n] == None):
if n<2:
mem[n] = n # 기반 상황 n<=1
else: # 일반 상황 otherwise
mem[n] = fib_dp_mem(n-1) + fib_dp_mem(n-2)
return mem[n]
mem = [None] * 6
print(fib(5))
print(fib_dp_mem(5))
print(fib_dp_tab(5))0-1 Knapsack
n 개의 물건의 각각 무게 (), 가치()와 용량이 w인 배낭이 주어졌을 때, 배낭 가치가 최대가 되도록 물건들을 넣는 문제이다. 배낭 용량을 초과하여 넣을 수 없고, 물건을 잘라서 일부만 넣는 것도 불가하다.
완전 탐색으로 풀 수 있으나 이므로 비효율적이다.
1) 점화식 정의
용량: W
물건의 갯수: n
물건: E1, E2, ..., En (각 물건은 () 형태로 무게와 가치를 가진다.)
k개의 물건을 넣는 배낭의 최대가치를 A(k, w)로 나타낸다.
즉, 구해야 하는 것은 A(n, w)이다.
기반 상황
배낭에 넣을 물건이 없다면 용량에 상관없이 최대 가치는 0이다.
A(0, w) = 0
배낭의 용량이 0일 때도 마찬가지로 물건에 상황없이 최대 가치는 0이다.
A(k, 0) = 0
일반 상황
-
Ek의 무게가 현재 배낭 용량 w보다 크면, Ek는 배당에 넣을 수 없고, E1~Ek-1 만 이용해서 계산한다.
즉, A(k, w) = A(k-1, w) -
Ek의 무게가 현재 배낭 용량 w 이하면, Ek 를 배낭에 넣을지 말지 결정한다.
-
Ek를 배낭에 넣는다면, 배낭의 가치는 val_k 만큼 증가되고, 용량이 w-wt_k가 된다. 이는 w-wt_k인 배낭에 E1~E_k-1 아이템을 넣는 문제를 해결하는 것과 같다.
즉, val_k + A(k-1, w-wt_k) -
Ek를 배낭에 넣지 않는다면, 이전 물건만 고려하면 된다.
즉, A(n-1, W)
-
이를 바탕으로 점화식을 구할 수 있다.
이 점화식을 기반으로 Divide and Conquer 방식으로 바로 구현할 수 있다.
이를 동적 계획법으로 바꾸기 위해서는 무게의 단위를 정수로 제한해야하고, 테이블을 설계해야한다.
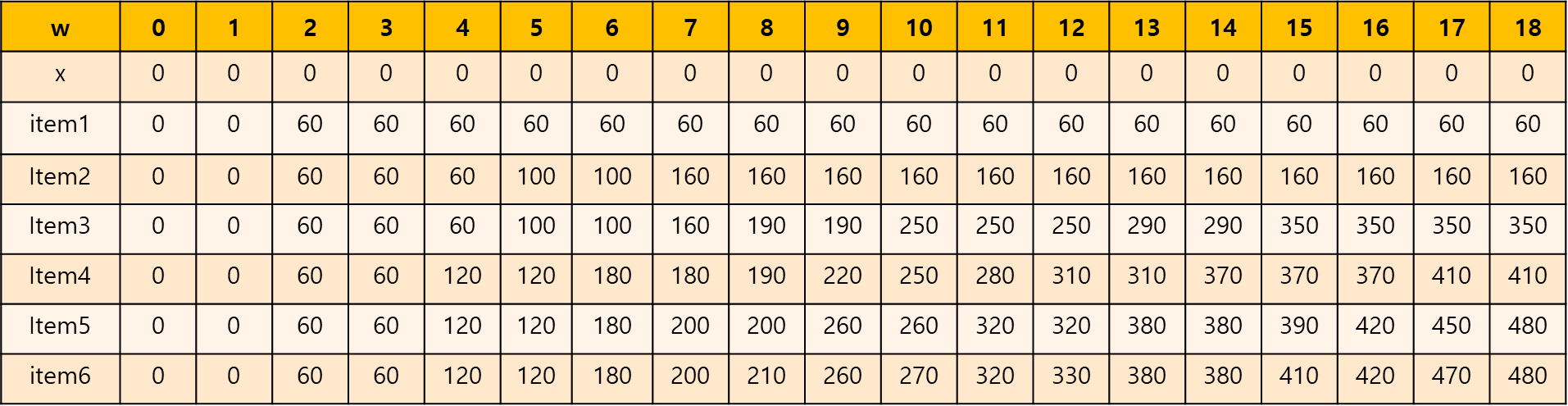
테이블은 (n+1) x (w+1)의 2차원 배열이다.

def knapSack_bf(w, wt, val, n):
if n==0 or w == 0:
return 0
if wt[n-1] > w:
return knapSack_bf(w, wt, val, n-1)
else:
valWithout = knapSack_bf(w, wt, val, n-1)
valWith = val[n-1] + knapSack_bf(w-wt[n-1], wt, val, n-1)
return max(valWith, valWithout)
def knapSack_dp(w, wt, val, n):
a = [[0 for x in range(w+1)] for x in range(n+1)]
for i in range(1, n+1):
for w in range(1, w+1):
if wt[i-1] > w:
a[i][w] = a[i-1][w]
else:
valWith = val[i-1] + a[i-1][w-wt[i-1]]
valWithout = a[i-1][w]
a[i][w] = max(valWith, valWithout)
return a[n][w]
val = [60, 100, 190, 120, 200, 150]
wt = [2, 5, 8, 4, 7, 6]
w = 18
n = len(val)
print("0-1배낭문제(분할 정복):", knapSack_bf(w, wt, val, n))
print("0-1배낭문제(동적 계획):", knapSack_dp(w, wt, val, n))dp로 구성하면
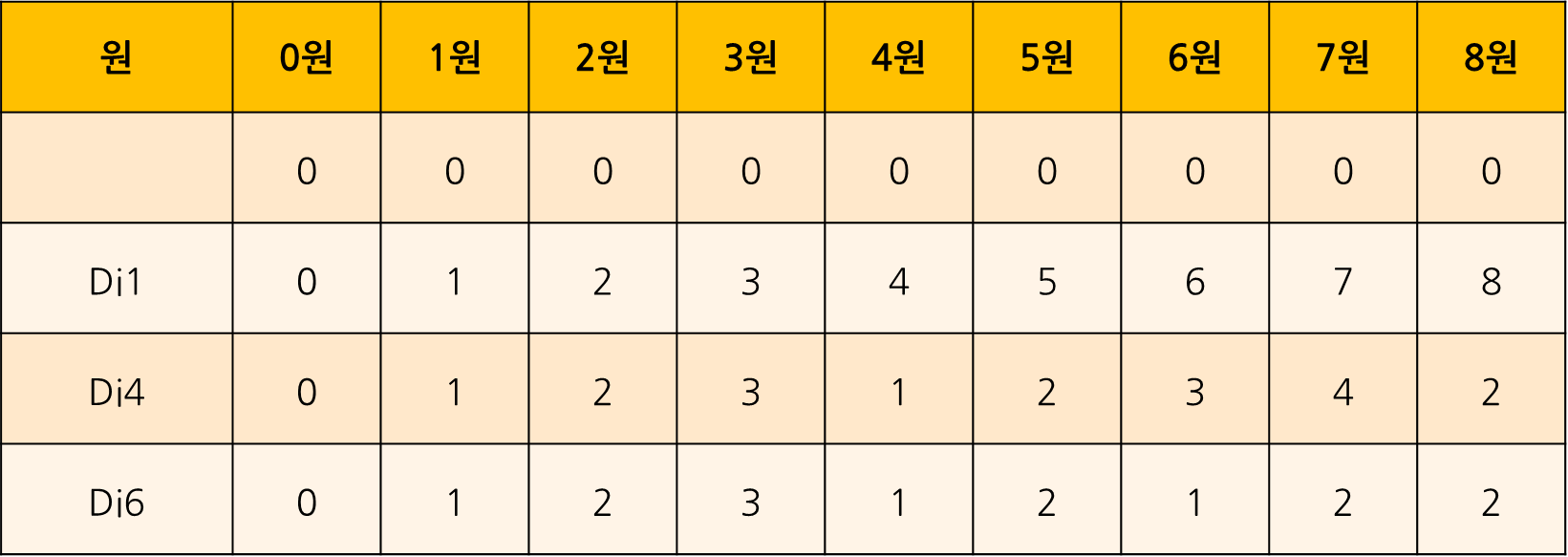
Coin DP
동전의 종류: 1원, 4원, 6원
8원을 거슬러주려 할때, 최소 동전의 수는?
점화식을 다음과 같이 구성해봤다.
교수님께서는 이 식에서 어차피 조건을 만족하든 안하든 otherwise 조건에서 동일한 식을 쓰게 되니, 그냥 나누지 않고, 한번에 하는 형식으로 바꾸신 것 같다.
def coin_dp():
mem[0] = 0
for i in range(1, n + 1):
mem[i] = mem[i - 1] + 1
for coin in coins:
if i >= coin:
mem[i] = min(mem[i], mem[i - coin] + 1)
coins = [1, 4, 6]
n = 8
mem = [None] * (n + 1)
coin_dp()
print("각 금액별 최소 동전의 수:", mem)
print("8원을 만드는 데 필요한 최소 동전의 수:", mem[8])
coin greedy
def min_coins_greedy(coins, v):
count = []
for i in range(len(coins)):
cnt = v//coins[i]
count.append(cnt)
v -= cnt * coins[i]
return count
coins = [500, 400, 100, 50, 10, 5, 1]
v = 800 # 그리디가 최적해를 찾는 경우가 아님의 반례.
print("잔돈:", v)
print("동전종류:", coins)
print("동전 개수:", min_coins_greedy(coins, v))이 문제는 위 문제와 다르게 하나의 리스트만 가지고 풀었다는 점이 해석해보니 흥미로워서 가져왔다. 어차피 전체 테이블을 만들어놔도, 이전 행의 같은 열만 보게 되므로 하나의 리스트를 각 행으로 순차적으로 업데이트 해가고, 아직 업데이트 되지 않은 열을 사용하며 구성되었다. 직관적이지는 않지만, 효율적인 방법인 것 같다.
LCS(Longest Common Subsequence)
두 데이터의 가장 긴 부분순서의 길이를 구하는 문제.
HELLO WORLD
GAME OVER
두 문자열의 최장 공통 부분 순서는 'E OR'이다.
DP를 이용해 해결할 수 있다.
두 문자열 길이가 각각 m, n
1) 기반 상황
n, m이 0이라면 LCS는 0이다.
2) 일반 상황
- 두 문자열의 마지막 문자가 같으면(xm = yn), 두 문자열 각각 마지막 문자를 제외한 LCS 길이를 구한 후 1을 더한다.
L[m-1][n-1] + 1
- 두 문자열의 마지막 문자가 다른 경우
max(L[m-1][n], L[m][n-1])- X에서 마지막 문자를 뺀 문자열과 Y 사이의 LCS
L[m-1][n] - Y에서 마지막 문자를 뺀 문자열과 X 사이의 LCS
L[m][n-1]
- X에서 마지막 문자를 뺀 문자열과 Y 사이의 LCS
이는 마지막 문자가 같을 때 count가 되고, 아닌 상황에서는 주어진 범위 내에서 최대값만 가져오는 형태이기 때문이다.
O(mn)
3) LCS 추적 알고리즘
LCS 길이 뿐 아니라, LCS 자체를 구하는 알고리즘. DP로 길이를 구하는 테이블을 제작했다면 이를 기반으로 추적 가능.
- LCS 요소 리스트 정의
- 최종 해가 저장된 우측 하단 셀에서 시작
- 현재 셀 값이 좌측, 좌측상담, 상단 방향으로 인접한 셀 보다 모두 크면 이 부분의 문자를 LCS 요소 리스트 전단에 삽입 후, 셀의 위치를 좌측 상단으로 이동.
- 3이 만족하지 않으면, 좌측 셀과 같고, 위족 셀보다 크면 왼쪽 이동
- 3, 4, 모두 만족하지 않으면 셀의 위치를 위로 옮김.
- i, j 0 될때까지 반복.
즉, 우측 하단은 크거나 같은 숫자, 좌측 상단 대각선 방향은 반전될 때가 겹치는 문자.
4) 구현
def lcs_dp(x, y):
m = len(x)
n = len(y)
l = [[None] * (n+1) for _ in range(m+1)]
for i in range(m+1):
for j in range(n+1):
if i==0 or j==0:
l[i][j] = 0
elif x[i-1] == y[j-1]:
l[i][j] = l[i-1][j-1] + 1
else:
l[i][j] = max(l[i-1][j], l[i][j-1])
for i in range(m+1):
print(l[i])
print("lcs =", lcs_dp_traceback(x, y, l))
def lcs_dp_traceback(x, y, l):
lcs = ""
i = len(x)
j = len(y)
while i>0 and j>0:
v = l[i][j]
if v > l[i][j-1] and v > l[i-1][j] and v > l[i-1][j-1]:
i-=1
j-=1
lcs = x[i] + lcs
elif v == l[i][j-1] and v > l[i-1][j]:
j -= 1
else:
i -= 1
return lcs
x = "game over"
y = "hello world"
print("x =", x)
print("y =", y)
print("lcs(dp)")
lcs_dp(x, y)7-4 백트레킹 기법(BackTracking)
DFS에서 어떤 노드가 해가 아니라고 판단되면 그 방향으로 더 탐색하지 않는 기법이다.
주요 문제
- N-Queen
- Permutations
- Maze Problem
- m-Coloring Problem
7-5 분기한정 기법(Branch and Bound)
백트레킹을 보완한 기법으로, 탐색하는 경계를 계산해 범위를 줄여나간다.
주요 문제
- 0-1 Knapsack
VIII. NP-완전문제와 근사 알고리즘
- 컴퓨터가 풀 수 있는 문제 (Tractable)
- 현실적인 시간(다항식 시간(Polynomial Time) O(n^k)) 안에 풀 수 있는 문제
- 현실적 시간안에 풀지 못하는 문제
ex. 지수 시간, 팩토리얼 시간 - 결정 문제(decision) 문제: Yes or No로 답하는 문제
- P 문제: 다항식(Polynomial) 시간에 해결할 수 있는 문제
- NP 문제: 비결정론적(Nondeterministic Polynomial) 다항식 시간 안에 해결 할 수 있는 결정 문제.
: 결정 문제의 답의 근거가 주어지면 근거가 옳음을 다항식 시간안에 확인 가능.
- 최적화(Optimization) 문제: 주어진 조건을 만족하는 최적해를 요구하는 문제
- 컴퓨터가 풀 수 없는 문제 (Intractable)
ex. Halting Problem
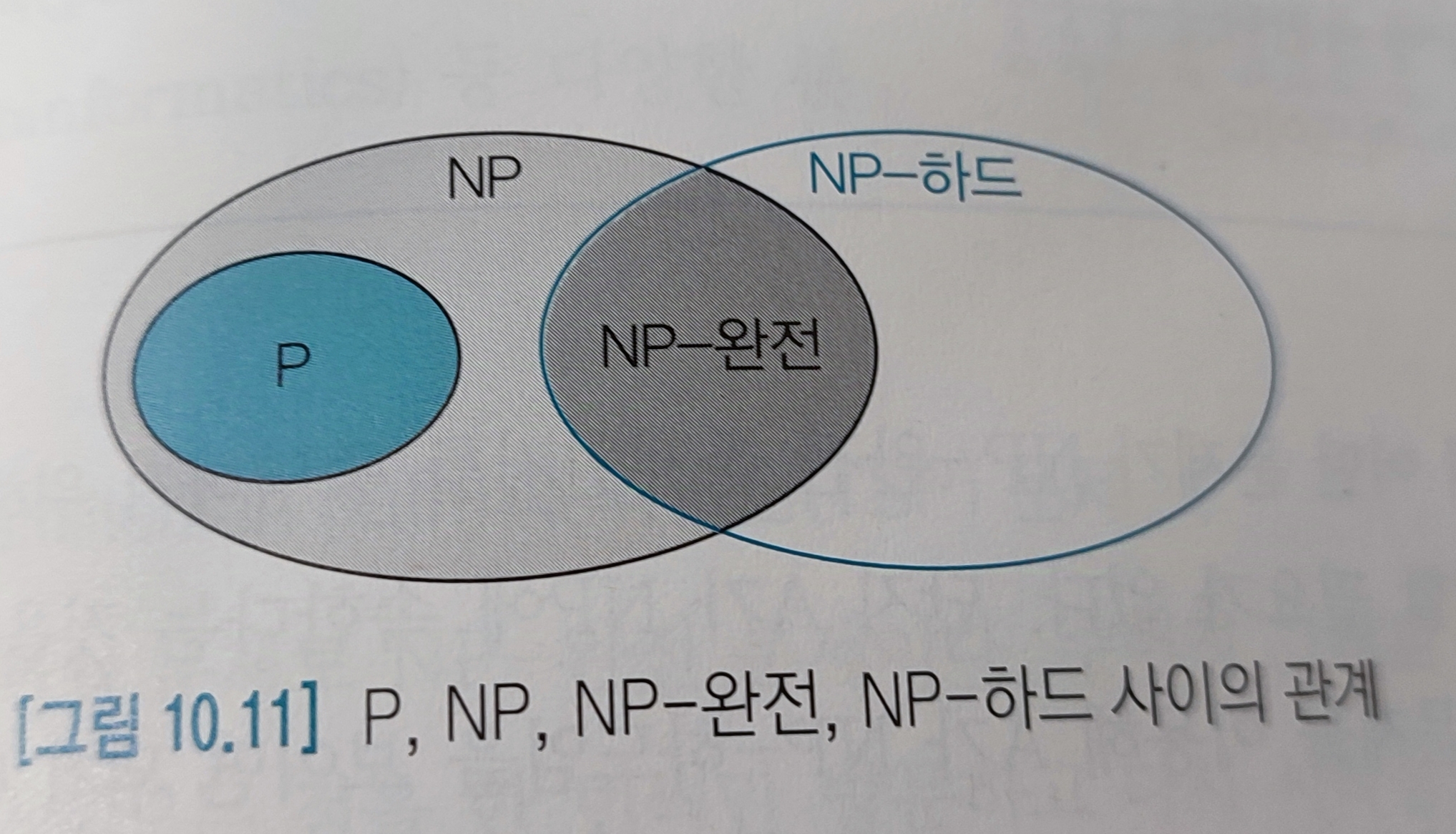
P C NP
모든 P문제는 NP에 속한다. 다항식 시간 안에 풀 수 잇는 문제는 답이 맞는지 확인하기 위해 비교해 보면 되기 때문이다.
NP-완전(Complete): 현재까지는 다항식 시간에 풀기 어렵지만, 다른 어려운 문제들과 논리적으로 밀접히 연결되어 있어 한 문제의 답을 구하면 다른 문제의 답을 구해 연쇄적으로 다항식 시간에 풀리게 됨.
NP-하드(Hard): 모든 np 문제는 다항식 시간에 문제 A로 변환할 수 있음을 문제 A가 만족하면, A는 NP-하드임.