[CS] Python 자료구조 정리

김두현·2024년 7월 14일

Computer Science Study

목록 보기

2/9

Updated on 2025.01.30.
~ ING

참고 서적

Do it! 자료구조와 함께 배우는 알고리즘 입문: 파이썬 편

윤성우의 열혈 자료구조

파이썬 알고리즘

I. 자료구조의 분류

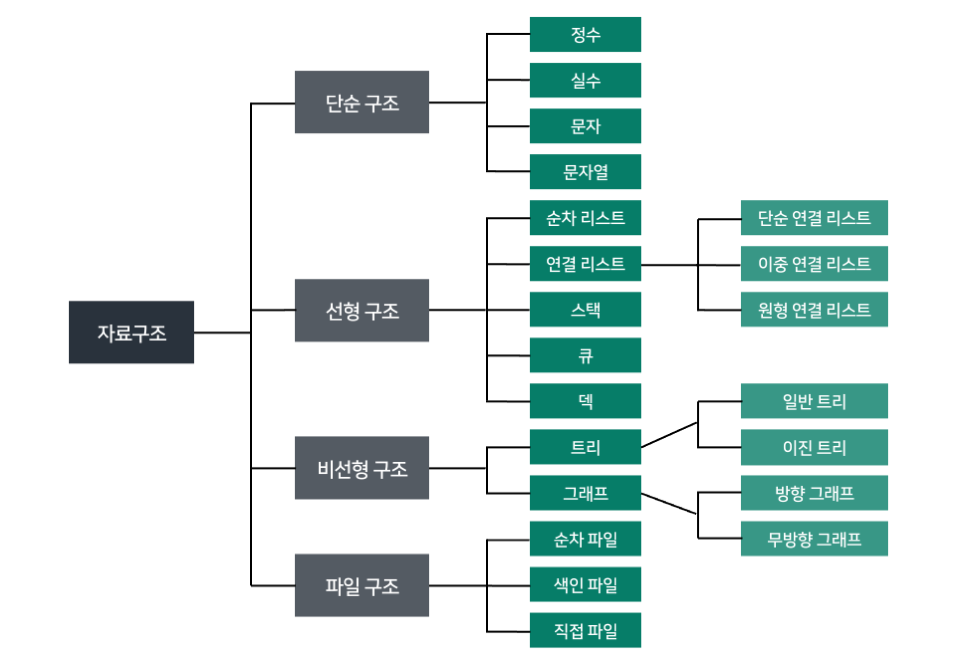
https://cheris8.github.io/python/DS-Overview/

II. 선형 자료구조

2-1 단순 연결 리스트(Linked List)

1) 개념

리스트(List) 자료구조는 데이터를 나란히 저장한다. 그리고 중복된 데이터의 저장을 막지 않는다.

순차 리스트: 배열을 기반으로 구현된 리스트
연결 리스트: 메모리의 동적 할당을 기반으로 구현된 리스트

다른 자료구조를 구현하는데 기반이 되는 자료구조이다.

2) ADT

def ListInit(self):
- 리스트 생성 후 제일 먼저 호출되어야 하는 함수
def LInsert(self, data):
- 리스트에 데이터를 저장한다. 매개변수 data에 전달된 값을 저장한다.
def LFirst(self):
- 첫번째 데이터가 pdata가 가리키는 메모리에 저장된다.
- 데이터의 참조를 위한 초기화가 진행된다.
- 참조 성공시 True, 실패시 False 반환.
def LNext(self):
- 참조된 데이터의 다음 데이터가 pdata가 가리키는 메모리에 저장된다.
- 순차적인 참조를 위해 반복호출이 가능하다.
- 참조를 새로 시작하려면 먼저 LFrist 함수를 호출해야한다.
- 참조 성공 시 True, 실패 시 False 반환
def LRemove(self):
- LFirst 또는 LNext 함수의 마지막 반환 데이터를 삭제한다.
- 삭제된 데이터는 반환된다.
- 마지막 반환 데이터를 삭제하므로 연이는 반복 호출을 허용하지 않는다.
def LCount(self):
- 리스트에 저장되어 있는 데이터 수를 반환한다.

3) 구현

import gc

class Node:
    def __init__(self, data = None, next = None):
        self.data = data
        self.next = next

class LinkedList:
    def __init__(self, head = None, cur = None, before = None, numOfData = None):
        self.head = head
        self.cur = cur
        self.before = before
        self.numOfData = numOfData

    def ListInit(self):
        self.head = Node()
        self.head.next = None
        self.numOfData = 0

    def LInsert(self, data):
        newNode = Node()

        newNode.data = data
        newNode.next = self.head.next

        self.head.next = newNode

        self.numOfData += 1

    def LFirst(self):
        if self.head.next == None:
            return False

        self.before = self.head
        self.cur = self.head.next

        self.pdata = self.cur.data
        return True 

    def LNext(self):
        if self.cur.next == None:
            return False
        
        self.before = self.cur
        self.cur = self.cur.next

        self.pdata = self.cur.data
        return True

    def LRemove(self):
        rpos = self.cur
        rdata = rpos.data

        self.before.next = self.cur.next
        self.cur = self.before

        del rpos
        gc.collect()

        self.numOfData -= 1

        return rdata

    def LCount(self):
        return self.numOfData
    

l = LinkedList()

l.ListInit()

l.LInsert(11)
l.LInsert(11)
l.LInsert(22)
l.LInsert(22)
l.LInsert(33)

print("남은 데이터 수: %d" %l.LCount())

# 조회
if l.LFirst():
    print(l.pdata, end = ' ')

    while(l.LNext()):
        print(l.pdata, end = ' ')
    
    print()
    print()

# 삭제
if l.LFirst(): 
    if l.pdata == 22:
        l.LRemove()

    while(l.LNext()):
        if l.pdata == 22:
            l.LRemove()

print("남은 데이터 수: %d" %l.LCount())

# 조회
if l.LFirst():
    print(l.pdata, end = ' ')

    while(l.LNext()):
        print(l.pdata, end = ' ')
    
    print()
    print()

2-2 원형 연결 리스트(Circular Linked List)

1) 개념

연결 리스트의 마지막 노드가 첫 번째 노드를 가리키는 연결 리스트.

2) 구현

① 연결 리스트 기반 구현

import gc

class Node:
    def __init__(self, data = None, next = None):
        self.data = data
        self.next = next

class CList:
    def __init__(self, tail = None, cur = None, before = None, numOfData = None):
        self.tail = tail
        self.cur = cur
        self.before = before
        self.numOfData = numOfData

    def ListInit(self):
        self.tail = None
        self.cur = None
        self.numOfData = 0

    def LInsert(self, data):
        newNode = Node()
        newNode.data = data

        if self.tail == None:
            self.tail = newNode
            newNode.next = newNode
        else:
            newNode.next = self.tail.next
            self.tail.next = newNode
            self.tail = newNode

        self.numOfData+=1

    def LInsertFront(self, data):
        newNode = Node()
        newNode.data = data

        if self.tail == None:
            self.tail = newNode
            newNode.next = newNode
        else:
            newNode.next = self.tail.next
            self.tail.next = newNode

        self.numOfData+=1

    def LFirst(self):
        if self.tail == None:
            return False

        self.before = self.tail
        self.cur = self.tail.next

        self.pdata = self.cur.data
        return True 

    def LNext(self):
        if self.tail == None:
            return False
        
        self.before = self.cur
        self.cur = self.cur.next

        self.pdata = self.cur.data
        return True

    def LRemove(self):
        rpos = self.cur
        rdata = rpos.data

        if rpos == self.tail:
            if self.tail == self.tail.next: # 마지막 노드
                self.tail = None
            else:
                self.tail = self.before

        self.before.next = self.cur.next
        self.cur = self.before

        del rpos
        gc.collect()

        self.numOfData -= 1

        return rdata

    def LCount(self):
        return self.numOfData
    

l = CList()
l.ListInit()

l.LInsert(3)
l.LInsert(4)
l.LInsert(5)
l.LInsertFront(2)
l.LInsertFront(1)

# 리스트에 저장된 데이터를 연속 3회 출력
if l.LFirst():
    print(l.pdata, end = ' ')

    for i in range(l.LCount()*3-1):
        if l.LNext():
            print(l.pdata, end = ' ')

    print()

# 2의 배수를 찾아서 모두 삭제
nodeNum = l.LCount()

if nodeNum != 0:
    l.LFirst()
    if l.pdata % 2 == 0:
        l.LRemove()
    
    for i in range(nodeNum-1):
        l.LNext()

        if l.pdata % 2 == 0:
            l.LRemove()

# 전체 데이터 1회 출력
if l.LFirst():
    print(l.pdata, end = ' ')

    for i in range(l.LCount()-1):
        if l.LNext():
            print(l.pdata, end= ' ')

    print()

② 배열 기반 구현

따로 원형 연결 리스트를 만든다기 보다 일반 리스트를 조건에 따라 원형 리스트처럼 활용할 수 있도록 구현한다.
ex) 일반 리스트를 조건에 따라 끝 index를 조회하면 처음부터 조회하도록 설정.

def ListInit(List):
    List = []

def LInsert(List, data):
    List.append(data)

def LInsertFront(List, data):
    List.insert(0, data)

def LRemove(List, i):
    return List.pop(i)

def LCount(List):
    return len(List)

# First와 Next가 필요없음.


List = []

ListInit(List)

LInsert(List, 3)
LInsert(List, 4)
LInsert(List, 5)
LInsertFront(List, 2)
LInsertFront(List, 1)


# 리스트에 저장된 데이터를 연속 3회 출력
for j in range(3):
    for i in List:
        print(i, end=' ')

print()


# 2의 배수를 찾아서 모두 삭제
i=0

while True:
    if i >= len(List):
        break
    
    if List[i]%2 ==  0:
        LRemove(List, i)
        i-=1
    
    i+=1

# 전체 데이터 1회 출력
for i in List:
    print(i, end=' ')

print()

2-3 양방향 연결 리스트(Doubly Linked List)

1) 개념

노드가 양쪽 방향으로 연결된 구조의 연결 리스트이다. 즉, 왼쪽 노드가 오른쪽 노드를 가리킴과 동시에 오른쪽 노드도 왼쪽 노드를 가리키는 구조이다.

양방향 연결 리스트 또는 이중 연결 리스트라고 불린다.

deque를 구현할 때 쓰인다.

2) 구현

① 연결 리스트 기반 구현

import gc

class Node:
    def __init__(self, data = None, next = None, prev = None):
        self.data = data
        self.next = next
        self.prev = prev

class DBLinkedList:
    def __init__(self, head = None, tail = None, cur = None, numOfData = None):
        self.head = head
        self.tail = tail
        self.cur = cur
        self.numOfData = numOfData

    def ListInit(self):
        self.head = Node()
        self.tail = Node()

        self.head.next = self.tail
        self.tail.prev = self.head

        self.head.prev = None
        self.tail.next = None

        self.numOfData = 0

    def LInsert(self, data):
        newNode = Node()

        newNode.data = data

        newNode.prev = self.tail.prev
        self.tail.prev.next = newNode

        newNode.next = self.tail
        self.tail.prev = newNode

        self.numOfData += 1

    def LFirst(self):
        if self.head.next == self.tail:
            return False

        self.cur = self.head.next
        self.pdata = self.cur.data

        return True 

    def LNext(self):
        if self.cur.next == self.tail:
            return False
        
        self.cur = self.cur.next
        self.pdata = self.cur.data

        return True

    def LPrevious(self):
        if self.cur.prev == self.head:
            return False
        
        self.cur = self.cur.prev
        self.pdata = self.cur.data

        return True
    
    def LRemove(self):
        rpos = self.cur
        rdata = rpos.data
        
        self.cur.prev.next = self.cur.next
        self.cur.next.prev = self.cur.prev

        self.cur = self.cur.prev

        del rpos
        gc.collect()

        self.numOfData -= 1

        return rdata

    def LCount(self):
        return self.numOfData
    
l = DBLinkedList()

l.ListInit()

# 데이터 삽입
l.LInsert(1)
l.LInsert(2)
l.LInsert(3)
l.LInsert(4)
l.LInsert(5)
l.LInsert(6)
l.LInsert(7)
l.LInsert(8)

# 데이터 조회
if l.LFirst():
    print(l.pdata, end=' ')

    while l.LNext():
        print(l.pdata, end=' ')

print()

if l.LFirst():
    if l.pdata % 2 == 0:
        l.LRemove()

    while l.LNext():
        if l.pdata % 2 ==0:
            l.LRemove()

# 저장된 데이터 재조회
if l.LFirst():
    print(l.pdata, end=' ')

    while l.LNext():
        print(l.pdata, end=' ')

print()

2-4 스택(Stack)

1) 개념

LIFO(Last-In, First-Out, 후입선출) 방식의 자료구조.

한쪽은 막히고 한쪽은 뚫려있는 초코볼 통에 비유한다.

2) ADT

def StackInit(self):
- 스택의 초기화 진행
- 스택 생성 후 가장 먼저 호출되어야 하는 함수
def SIsEmpty(self):
- 스택이 빈 경우 True, 그렇지 않은 경우 False 반환
def SPush(self, data):
- 스택에 데이터를 저장한다.
def SPop(self):
- 마지막에 저장되는 요소를 삭제한다.
- 삭제된 데이터는 반환된다.
- 본 함수의 호출을 위해서는 데이터가 하나 이상 존재함이 보장되어야 한다.
def SPeek(self):
- 마지막에 저장된 요소를 반환하되 삭제하지 않는다.
- 본 함수의 호출을 위해서는 데이터가 하나 이상 존재함이 보장되어야 한다.

3) 구현

① 연결 리스트 기반 구현

import gc

class Node:
    def __init__(self, data = None, next = None):
        self.data = data
        self.next = next

class ListStack:
    def __init__(self, head = None):
        self.head = head

    def StackInit(self):
        self.head = None

    def SIsEmpty(self):
        if self.head == None:
            return True
        else:
            return False

    def SPush(self, data):
        newNode = Node()

        newNode.data = data
        newNode.next = self.head

        self.head = newNode

    def SPop(self):
        if self.SIsEmpty():
            print("Stack Memory Error!")
            exit()
        
        rdata = self.head.data
        rnode = self.head


        self.head = self.head.next

        del rnode
        gc.collect()

        return rdata

    def SPeek(self):
        if self.SIsEmpty():
            print("Stack Memory Error!")
            exit()

        return self.head.data
    

stack = ListStack()

stack.StackInit()

# 데이터 넣기
stack.SPush(1)
stack.SPush(2)
stack.SPush(3)
stack.SPush(4)
stack.SPush(5)

# 데이터 꺼내기
while not stack.SIsEmpty():
    print(stack.SPop(), end=' ')

② 배열 기반 구현

리스트를 Stack으로 사용.

def StackInit(stack):
    stack = []

def SIsEmpty(stack):
    if not stack:
        return True
    else:
        return False

def SPush(stack, data):
    stack.append(data)

def SPop(stack):
    if SIsEmpty(stack):
        print("Stack Memory Error!")
        exit()
    else:
        return stack.pop()

def SPeek(stack):
    if SIsEmpty(stack):
        print("Stack Memory Error!")
        exit()
    else:
        return stack[-1]

stack = []

StackInit(stack)

# 데이터 넣기
SPush(stack, 1)
SPush(stack, 2)
SPush(stack, 3)
SPush(stack, 4)
SPush(stack, 5)

# 데이터 꺼내기
while not SIsEmpty(stack):
    print(SPop(stack), end=' ')

2-5 큐(Queue)

1) 개념

FIFO(First-In, First Out) 구조의 자료 구조

대중교통에서 줄을 서는 경우로 비유

뒤로 넣고 앞으로 빼는 자료구조

2) ADT

def QueueInit(self):
- 큐의 초기화 진행한다.
- 큐 생성 후 제일 먼저 호출되어야 하는 함수이다.
def QIsEmpty(self):
- 큐가 빈 경우 True, 그렇지 않은 경우 False를 반환한다.
def Enqueue(self, data):
- 큐에 데이터를 저장한다.
def Dequeue(self):
- 저장순서가 가장 앞선 데이터를 삭제한다.
- 삭제된 데이터는 반환한다.
- 본 함수의 호출을 위해서는 데이터가 하나 이상 존재함이 보장되어야 한다.
def QPeek(self):
- 저장순서가 가장 앞선 데이터를 반환하되 삭제하지 않는다.
- 본 함수의 호출을 위해서는 데이터가 하나 이상 존재함이 보장되어야 한다.

3) 구현

① 연결 리스트 기반 구현

import gc

class Node:
    def __init__(self, data = None, next = None):
        self.data = data
        self.next = next

class LQueue:
    def __init__(self, front = None, rear = None):
        self.front = front
        self.rear = rear

    def QueueInit(self):
        self.front = None
        self.rear = None

    def QIsEmpty(self):
        if self.front == None:
            return True
        else:
            return False

    def Enqueue(self, data):
        newNode = Node()
        
        newNode.next = None
        newNode.data = data

        if self.QIsEmpty():
            self.front = newNode
            self.rear = newNode
        else:
            self.rear.next = newNode
            self.rear = newNode

    def Dequeue(self):
        if self.QIsEmpty():
            print("Queue Memory Error!")
            exit()

        delNode = self.front
        retData = self.front.data
        self.front = self.front.next

        del delNode
        gc.collect()

        return retData

    def QPeek(self):
        if self.QIsEmpty():
            print("Queue Memory Error!")
            exit()

        return self.front.data
    
q = LQueue()

q.QueueInit()

q.Enqueue(1)
q.Enqueue(2)
q.Enqueue(3)
q.Enqueue(4)
q.Enqueue(5)

while not q.QIsEmpty():
    print(q.Dequeue())

print(q.Dequeue())

② Deque 라이브러리 기반 구현

python 표준 라이브러리 collections에 있는 deque를 사용해 Queue를 구현한다.
(list를 활용해 Queue를 구현할 수 있지만, Dequeue 연산시 list.pop(0)를 써야한다. 이때, list.pop(0) 연산은 list가 빈 index 자리를 채워넣어야 하므로 O(n) 연산을 하게 된다. 따라서, 시간복잡도 상 deque를 쓰는게 훨씬 효율적이다.)

from collections import deque

def QueueInit(queue):
    queue= deque()

def QIsEmpty(queue):
    if not queue:
        return True
    else:
        return False

def Enqueue(queue, data):
    queue.append(data)

def Dequeue(queue):
    if QIsEmpty(queue):
        print("Queue Memory Error!")
        exit()
    else:
        return queue.popleft()

def QPeek(queue):
    if QIsEmpty(queue):
        print("Queue Memory Error!")
        exit()
    else:
        return queue[-1]

queue= deque()

QueueInit(queue)

Enqueue(queue, 1)
Enqueue(queue, 2)
Enqueue(queue, 3)
Enqueue(queue, 4)
Enqueue(queue, 5)

while not QIsEmpty(queue):
    print(Dequeue(queue),end=' ')
    
print()

print(Dequeue(queue))

2-6 덱(Deque)

1) 개념

앞으로도 뒤로도 넣을 수 있고, 앞으로도 뒤로도 뺄 수 있는 자료구조이다.

양방향 리스트로 구현하기 편리하다.

2) ADT

def dequeInit(Deque):
- 덱의 초기화를 진행한다.
- 덱 생성 후 제일 먼저 호출되어야 하는 함수이다.
def dequeIsEmpty(Deque):
- 덱이 빈 경우 True를, 그렇지 않은 경우는 False를 반환한다.
def dequeAddFirst(Deque, data):
- 덱의 머리에 데이터를 저장한다.
def dequeAddLast(Deque, data):
- 덱의 꼬리에 데이터를 저장한다.
def dequeRemoveFirst(Deque):
- 덱의 머리에 위치한 데이터를 반환 및 소멸한다.
def dequeRemoveLast(Deque):
- 덱의 꼬리에 위치한 데이터를 반환 및 소멸한다.
def dequeGetFirst(Deque):
- 덱의 머리에 위치한 데이터를 소멸하지 않고 반환한다.
def dequeGetLast(Deque):
- 덱의 꼬리에 위치한 데이터를 소멸하지 않고 반환한다.

3) 구현

① 양방향 연결 리스트 기반 구현

import gc

class Node:
    def __init__(self, data = None, next = None, prev = None):
        self.data = data
        self.next = next
        self.prev = prev

class DLDeque:
    def __init__(self, head = None, tail = None):
        self.head = head
        self.tail = tail

    def DequeInit(self):
        self.head = None
        self.tail = None

    def DQIsEmpty(self):
        if self.head == None:
            return True
        else:
            return False

    def DQAddFirst(self, data):
        newNode = Node()

        newNode.data = data
        newNode.next = self.head
        newNode.prev = None

        if self.DQIsEmpty():
            self.tail = newNode
        else:
            self.head.prev = newNode

        self.head = newNode

    def DQAddLast(self, data):
        newNode = Node()
        
        newNode.data = data
        newNode.prev = self.tail
        newNode.next = None
        
        if self.DQIsEmpty():
            self.head = newNode
        else:
            self.tail.next = newNode

        self.tail = newNode

    def DQRemoveFirst(self):
        rnode = self.head

        if self.DQIsEmpty():
            print("Deque Memory Error !")
            exit()
        
        rdata = self.head.data
        
        self.head = self.head.next

        del rnode
        gc.collect()

        if self.head == None:
            self.tail = None
        else:
            self.head.prev = None

        return rdata


    def DQRemoveLast(self):
        rnode = self.tail

        if self.DQIsEmpty():
            print("Deque Memory Error !")
            exit()

        rdata = self.tail.data
        self.tail = self.tail.prev

        del rnode
        gc.collect()

        if self.tail == None:
            self.head = None
        else:
            self.tail.next = None

        return rdata

    def DQGetFirst(self):
        if self.DQIsEmpty():
            print("Deque Memory Error !")
            exit()
        
        return self.head.data

    def DQGetLast(self):
        if self.DQIsEmpty():
            print("Deque Memory Error !")
            exit()

        return self.tail.data


deq = DLDeque()

deq.DequeInit()

# 데이터 넣기 1
deq.DQAddFirst(3)
deq.DQAddFirst(2)
deq.DQAddFirst(1)

deq.DQAddLast(4)
deq.DQAddLast(5)
deq.DQAddLast(6)


# 데이터 꺼내기 1
while not deq.DQIsEmpty():
    print(deq.DQRemoveFirst(), end=' ')
print()

# 데이터 넣기 2
deq.DQAddFirst(3)
deq.DQAddFirst(2)
deq.DQAddFirst(1)

deq.DQAddLast(4)
deq.DQAddLast(5)
deq.DQAddLast(6)

# 데이터 꺼내기 2
while not deq.DQIsEmpty():
    print(deq.DQRemoveLast(), end=' ')
print()

② Deque 라이브러리 기반 구현

python 표준 라이브러리 collections에 있는 deque를 사용해 deque를 구현한다.

from collections import deque
def DequeInit(Deque):
    Deuqe = deque()

def DQIsEmpty(Deque):
    if not Deque:
        return True
    else:
        return False

def DQAddFirst(Deque, data):
    Deque.appendleft(data)

def DQAddLast(Deque, data):
    Deque.append(data)

def DQRemoveFirst(Deque):
    if DQIsEmpty(Deque):
        print("Deque Memory Error !")
    else:
        return Deque.popleft()

def DQRemoveLast(Deque):
    if DQIsEmpty(Deque):
        print("Deque Memory Error !")
    else:
        return Deque.pop()

def DQGetFirst(Deque):
    if DQIsEmpty(Deque):
        print("Deque Memory Error !")
    else:
        return Deque[0]

def DQGetLast(Deque):
    if DQIsEmpty(Deque):
        print("Deque Memory Error !")
    else:
        return Deque[-1]


Deque = deque()

DequeInit(Deque)

# 데이터 넣기 1
DQAddFirst(Deque, 3)
DQAddFirst(Deque, 2)
DQAddFirst(Deque, 1)

DQAddLast(Deque, 4)
DQAddLast(Deque, 5)
DQAddLast(Deque, 6)

# 데이터 꺼내기 1
while not DQIsEmpty(Deque):
    print(DQRemoveFirst(Deque), end=' ')
print()

# 데이터 넣기 2
DQAddFirst(Deque, 3)
DQAddFirst(Deque, 2)
DQAddFirst(Deque, 1)

DQAddLast(Deque, 4)
DQAddLast(Deque, 5)
DQAddLast(Deque, 6)

# 데이터 꺼내기 2
while not DQIsEmpty(Deque):
    print(DQRemoveLast(Deque), end=' ')
print()

2-7 우선순위 큐(Priorty Queue)

1) 개념

들어간 순서에 상관없이 우선순위가 높은 데이터가 먼저 나오는 자료구조

힙 자료구조를 활용해서 쉽게 구현할 수 있다.

2) ADT

def PQueueInit(self, pc):
- 우선순위 큐의 초기화를 진행한다.
- 우선순위 큐 생성 후 제일 먼저 호출되어야 하는 함수이다.
def PQIsEmpty(self):
- 우선순위 큐가 빈 경우 True를, 그렇지 않은 경우 False를 반환한다.
def PEnqueue(self, data):
- 우선순위 큐에 데이터를 저장한다. 매개변수 data로 전달된 값을 저장한다.
def PDequeue(self):
- 우선순위가 가장 높은 데이터를 삭제한다.
- 삭제된 데이터는 반환된다.
- 본 함수의 호출을 위해서는 데이터가 하나 이상 존재함이 보장되어야 한다.

3) 구현

① 힙 기반 구현

힙 자료구조를 활용한 구현.

HEAP_LEN = 100

class Heap:
    def __init__(self, numOfData = None, pc = None, heapList = None):
        self.numOfData = numOfData
        self.pc = pc
        self.heapList = heapList

    def HeapInit(self, pc):
        self.numOfData = 0
        self.comp = pc 

        self.heapList = [None for i in range(HEAP_LEN)]

    def HIsEmpty(self):
        if self.numOfData == 0:
            return True
        else:
            return False
        
    def GetHiPriChildIDX(self, idx):
        if GetLChildIDX(idx) > self.numOfData:
            return False
        
        elif GetLChildIDX(idx) == self.numOfData:
            return GetLChildIDX(idx)
        
        else:
            if self.comp(self.heapList[GetLChildIDX(idx)], self.heapList[GetRChildIDX(idx)]) < 0:
                return GetRChildIDX(idx)
            else:
                return GetLChildIDX(idx)

    def HInsert(self, data):
        idx = self.numOfData+1

        while idx != 1:
            if self.comp(data, self.heapList[GetParentIDX(idx)]) > 0:
                self.heapList[idx] = self.heapList[GetParentIDX(idx)]
                idx = GetParentIDX(idx)
            else:
                break
        
        self.heapList[idx] = data
        self.numOfData += 1


    def HDelete(self):
        retData = self.heapList[1]
        lastElem = self.heapList[self.numOfData]

        parentIdx = 1

        while True:
            childIdx = self.GetHiPriChildIDX(parentIdx)

            if not childIdx:
                break

            if self.comp(lastElem, self.heapList[childIdx]) >= 0:
                break

            self.heapList[parentIdx] = self.heapList[childIdx]
            parentIdx = childIdx

        self.heapList[parentIdx] = lastElem
        self.numOfData -= 1

        return retData
    
class PQueue():
    def __init__(self):
        self.heap = Heap()

    def PQueueInit(self, pc):
        self.heap.HeapInit(pc)

    def PQIsEmpty(self):
        return self.heap.HIsEmpty()
    
    def PEnqueue(self, data):
        self.heap.HInsert(data)

    def PDequeue(self):
        return self.heap.HDelete()
    
def GetParentIDX(idx):
    return idx//2

def GetLChildIDX(idx):
    return idx*2

def GetRChildIDX(idx):
    return GetLChildIDX(idx) + 1

# main

def DataPriorityComp(ch1, ch2):
    return ord(ch2)-ord(ch1) # minheap
    # return ch1-ch2 # maxheap

    # 첫번째 인자 우선 순위 > 두번째 인자 우선순위: 0보다 큰 값 반환
    # 첫번째 인자 우선 순위 < 두번째 인자 우선순위: 0보다 작은 값 반환
    # 첫번째 인자 우선 순위 = 두번째 인자 우선순위: 0 반환

pq = PQueue()
pq.PQueueInit(pc = DataPriorityComp)

pq.PEnqueue('A')
pq.PEnqueue('B')
pq.PEnqueue('C')
print(pq.PDequeue())

pq.PEnqueue('A')
pq.PEnqueue('B')
pq.PEnqueue('C')
print(pq.PDequeue())

while not pq.PQIsEmpty():
    print(pq.PDequeue())

② Heapq 라이브러리 기반 구현

heapq 모듈을 활용해서 구현하면 쉽게 구현할 수 있다.

import heapq

def PQueueInit(pq):
    pq = []

def PQIsEmpty(pq):
    if not pq:
        return True
    else:
        return False

def PEnqueue(pq, data):
    heapq.heappush(pq, data)

def PDequeue(pq):
    if PQIsEmpty(pq):
        print("Priority Queue Memory Error !")
    else:
        return heapq.heappop(pq)


pq = []
PQueueInit(pq)

PEnqueue(pq, 'A')
PEnqueue(pq, 'B')
PEnqueue(pq, 'C')
print(PDequeue(pq))

PEnqueue(pq, 'A')
PEnqueue(pq, 'B')
PEnqueue(pq, 'C')
print(PDequeue(pq))

while not PQIsEmpty(pq):
    print(PDequeue(pq))

III. 비선형 자료구조

3-1 이진 트리(Binary Tree)

1) 개념

트리는 계층적 관계(Hierarchical Relationship)을 표현하는 자료구조이다.

트리의 용어

노드(node): 트리의 각 구성요소
간선(edge): 노드와 노드를 연결하는 연결선
루트 노드(root node): 트리 구조에서 최상위에 존재하는 노드
단말 노드(terminal node, leaf node): 아래오 또 다른 노드가 연결되어 있는 않는 노드
내부 노드(internal node, nonterminal node): 단말 노드를 제외한 모든 노드
레벨(level): 루트노드에서 얼마나 멀리 떨어져 있는지를 나타낸다. 루트의 레벨은 0이고, 가지가 하나씩 아래로 뻗어 내려갈 때마다 1씩 증가한다.
부모(parent): 어떤 노드와 가지가 연결됐을 대 가장 위쪽에 있는 노드
자식(child): 어떤 노드와 가지가 연결됐을 때 아래쪽 노드
형제(sibling): 부모가 같은 노드
조상(ancestor): 어떤 노드에서 위쪽으로 가지를 따라가면 만나는 모든 노드
자손(descentdant): 어떤 노드에서 아래쪽으로 가지를 따라가면 만나는 모든 노드
차수(degree): 각 노드가 갖는 자식의 수
높이(height): 루트에서 가장 멀리 있는 단말 노드까지의 거리. 즉, 단말 노드의 레벨의 최댓값.
서브 트리(Subtree): 어떤 노드를 루트로 하고, 그 자손으로 구성된 트리
빈 트리(Null tree, None tree): 노드와 가지가 전혀 없는 트리

형제 노드의 순서 관계에 따른 트리 분류

순서 트리(ordered tree): 형제 노드의 순서 관계가 있는 트리
무순서 트리(unordered tree): 형제 노드의 순서 관계를 구별하지 않는 트리

이진 트리 분류 용어

이진트리(Binary tree): 왼쪽 자식과 오른쪽 자식을 갖는 트리. 루트 노드를 중심으로 둘로 나뉘는 두 개의 서브 트리도 이진 트리여야 하고, 그 서브 트리의 모든 서브 트리도 이진 트리여야 한다. 자식이 없어도, 공집합(empty set) 노드가 존재하는 것으로 간주하기 때문에 자식이 있다고 간주.

포화 이진 트리(Full Binary Tree): 모든 레벨이 꽉 찬 이진 트리
완전 이진 트리(Complete Binary Tree): 레벨이 꽉 찬 상태는 아니지만, 노드가 위 아래로 왼쪽에서 오른쪽 순서대로 채워진 상태.

트리의 순회

전위 순회(Preorder Traversal): 루트 노드 → 왼쪽 자식 노드 → 오른쪽 자식 노드
중위 순회(Inorder Traversal): 왼쪽 자식 노드 → 루트 노드 → 오른쪽 자식 노드
후위 순회(Postorder Traversal): 왼쪽 자식 노드 → 오른쪽 자식 노드 → 루트 노드

2) ADT

def MakeBTreeNode(self):
- 이진 트리 노드를 생성하고 그 주소값을 반환한다.
def GetData(self):
- 노드에 저장된 데이터를 반환한다.
def SetData(self, data):
- 노드에 데이터를 저장한다. data로 전달된 값을 저장한다.
def GetLeftSubTree(self):
- 왼쪽 서브 트리의 주소 값을 반환한다.
def GetRightSubTree(self):
- 오른쪽 서브 트리의 주소 값을 반환한다.
def MakeLeftSubTree(self, sub):
- 왼쪽 서브 트리를 연결한다.
def MakeRightSubTree(self, sub):
- 오른쪽 서브 트리를 연결한다.

3) 구현

① Linked List 기반 구현

import gc

class BTreeNode:
    def __init__(self, data = None, left = None, right = None):
        self.data = data
        self.left = left
        self.right = right

    def MakeBTreeNode(self):
        nd = BTreeNode()

        nd.left = None
        nd.right = None

        return nd

    def GetData(self):
        return self.data

    def SetData(self, data):
        self.data = data

    def GetLeftSubTree(self):
        return self.left

    def GetRightSubTree(self):
        return self.right

    def MakeLeftSubTree(self, sub):
        if self.left != None:
            del self.left
            gc.collect()
        
        self.left = sub

    def MakeRightSubTree(self, sub):
        if self.right != None:
            del self.right
            gc.collect()
        
        self.right = sub    

def InorderTraverse(bt):
    if bt == None:
        return
    
    InorderTraverse(bt.left)
    print(bt.data)
    InorderTraverse(bt.right)

def PreorderTraverse(bt):
    if bt == None:
        return
    
    print(bt.data)
    PreorderTraverse(bt.left)
    PreorderTraverse(bt.right)

def PostorderTraverse(bt):
    if bt == None:
        return
    
    PostorderTraverse(bt.left)
    PostorderTraverse(bt.right)
    print(bt.data)


def DeleteTree(bt): # 후위 순회 하면서 소멸
    if bt == None:
        return
    
    DeleteTree(bt.left)
    DeleteTree(bt.right)

    print("del tree data: %s" %bt.data)

    del bt
    gc.collect()
    

bt1 = BTreeNode()
bt1.MakeBTreeNode()

bt2 = BTreeNode()
bt2.MakeBTreeNode()

bt3 = BTreeNode()
bt3.MakeBTreeNode()

bt4 = BTreeNode()
bt4.MakeBTreeNode()

bt1.SetData(1)
bt2.SetData(2)
bt3.SetData(3)
bt4.SetData(4)

bt1.MakeLeftSubTree(bt2)
bt1.MakeRightSubTree(bt3)
bt2.MakeLeftSubTree(bt4)

print(bt1.GetLeftSubTree().GetData())

print(bt1.GetLeftSubTree().GetLeftSubTree().GetData())

print()
PreorderTraverse(bt1)
print()
InorderTraverse(bt1)
print()
PostorderTraverse(bt1)
print()

DeleteTree(bt1)

② 배열 기반 구현

배열 기반 이진트리를 활용하여 간단하게 구현할 수 있다.

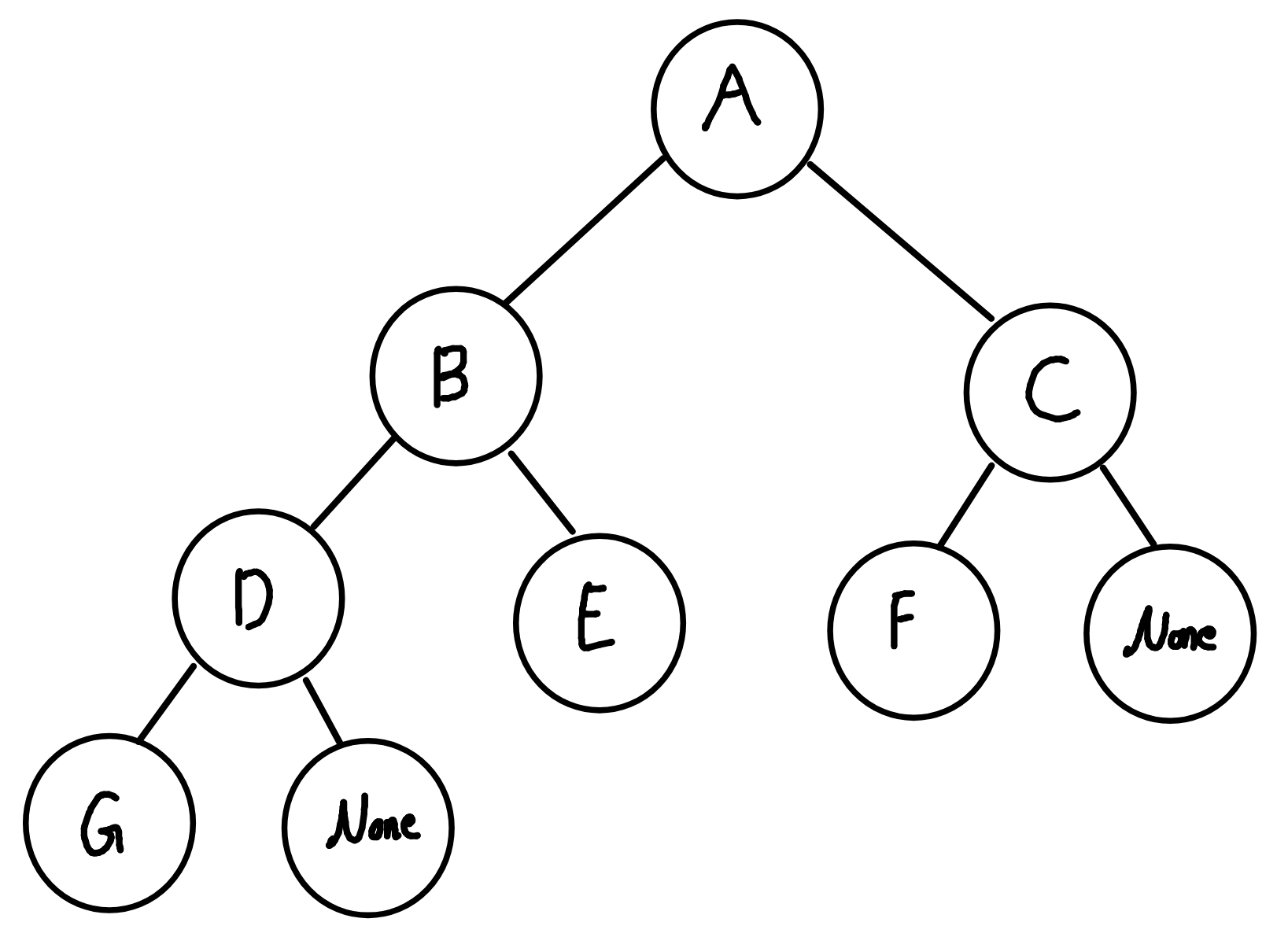
위와 같이 이진트리가 구성되어 있을 때, 다음과 같이 배열을 구성한다. 0번째 인덱스는 사용하지 않고, 1번째 인덱스부터 각 level의 왼쪽부터 채운다.

index	0	1	2	3	4	5	6	7	8
value	-	A	B	C	D	E	F	None	G

산술연산자

왼쪽 자식 노드의 인덱스 값 = 부모 노드의 인덱스 값 * 2
오른쪽 자식 노드의 인덱스 값 = 부모 노드의 인덱스 값 * 2 + 1
부모 노드의 인덱스 값 = 자식 노드의 인덱스 값 // 2

비트연산자

왼쪽 자식 노드의 인덱스 값 = 부모 노드의 인덱스 값 << 2
오른쪽 자식 노드의 인덱스 값 = (부모 노드의 인덱스 값 << 2) | 1
부모 노드의 인덱스 값 = 자식 노드의 인덱스 값 >> 2
형제 노드의 인덱스 값 = 다른 형제 노드의 인덱스 값 ^ 1

def MakeBTreeNode():
    bTree = [None] * 100

    return bTree

def GetData(bTree, n):
    return bTree[n]

def SetData(bTree, n, data):
    bTree[n] = data

def GetLeftSubTree(n):
    return n*2

def GetRightSubTree(n):
    return n*2+1

def MakeLeftSubTree(bTree, n, data):
    bTree[n*2] = data

def MakeRightSubTree(bTree, n, data):
    bTree[n*2+1] = data

def DeleteTree(bTree):
    del bTree

def InorderTraverse(bTree, n):
    if bTree[n] == None:
        return

    InorderTraverse(bTree, n*2)
    print(bTree[n])
    InorderTraverse(bTree, n*2+1)

def PreorderTraverse(bTree, n):
    if bTree[n] == None:
        return
    
    print(bTree[n])
    PreorderTraverse(bTree, n*2)
    PreorderTraverse(bTree, n*2+1)

def PostorderTraverse(bTree, n):
    if bTree[n] == None:
        return
    
    PostorderTraverse(bTree, n*2)
    PostorderTraverse(bTree, n*2+1)
    print(bTree[n])

bTree = MakeBTreeNode()

SetData(bTree, 1, 1)
MakeLeftSubTree(bTree, 1, 2)
MakeRightSubTree(bTree, 1, 3)

MakeLeftSubTree(bTree, 2, 4)

print(GetData(bTree, GetLeftSubTree(1)))
print(GetData(bTree, GetLeftSubTree(GetLeftSubTree(1))))

print()
PreorderTraverse(bTree, 1)
print()
InorderTraverse(bTree, 1)
print()
PostorderTraverse(bTree, 1)
print()

DeleteTree(bTree)

3-2 힙(Heap)

1) 개념

정의

힙은 모든 노드에 저장된 값은 자식 노드에 저장된 값보다 크거나 같아야 한다.
즉, 루트 노드에 저장된 값이 가장 커야하는 이진 트리이되, 완전 이진 트리이다.

힙의 분류

최대 힙(max heap): 루트 노드로 올라갈수록 저장된 값이 커지는 완전 이진 트리
최소 힙(min heap): 루트 노드로 올라갈수록 저장된 값이 작아지는 완전 이진 트리.

힙의 데이터 추가 과정

새로운 데이터를 우선 순위가 제일 낮다는 가정하에 '마지막 위치'에 저장한다.
부모 노드와 우선순위를 비교해서 위치가 바뀌어야 한다면 바꾼다.
제대로 된 위치를 찾을 때까지 2번을 반복한다.

여기서 '마지막 위치'는 마지막 레벨의 가장 오른쪽 위치를 뜻한다.

힙의 데이터 삭제 과정

루트 노드를 삭제한다.
'마지막 위치'의 노드를 루트 노드 자리로 옮긴다.
루트 노드가 자식 노드보다 우선 순위가 높은지 비교한다. 자식 노드가 우선 순위가 높다면 자식 노드 중 우선 순위가 높은 자식노드와 교환한다.
자식보드가 우선 순위가 낮을 때까지 3번 과정을 반복한다.

힙의 시간 복잡도

힙 기반 데이터 저장의 시간 복잡도: $log_2n$
힙 기반 데이터 삭제의 시간 복잡도: $log_2n$

리스트 시간 복잡도

리스트 기반 데이터 저장의 시간 복잡도: $n$
리스트 기반 데이터 삭제의 시간 복잡도: $1$

즉, 리스트 기반 데이터의 저장 및 삭제의 시간복잡도가 힙이 훨씬 작음을 알 수 있다.

2) 구현

① Class 기반 구현

HEAP_LEN = 100

class Heap:
    def __init__(self, numOfData = None, pc = None, heapList = None):
        self.numOfData = numOfData
        self.pc = pc
        self.heapList = heapList

    def HeapInit(self, pc):
        self.numOfData = 0
        self.comp = pc 

        self.heapList = [None for i in range(HEAP_LEN)]

    def HisEmpty(self):
        if self.numOfData == 0:
            return True
        else:
            return False
        
    def GetHiPriChildIDX(self, idx):
        if GetLChildIDX(idx) > self.numOfData:
            return False
        
        elif GetLChildIDX(idx) == self.numOfData:
            return GetLChildIDX(idx)
        
        else:
            if self.comp(self.heapList[GetLChildIDX(idx)], self.heapList[GetRChildIDX(idx)]) < 0:
                return GetRChildIDX(idx)
            else:
                return GetLChildIDX(idx)

    def HInsert(self, data):
        idx = self.numOfData+1

        while idx != 1:
            if self.comp(data, self.heapList[GetParentIDX(idx)]) > 0:
                self.heapList[idx] = self.heapList[GetParentIDX(idx)]
                idx = GetParentIDX(idx)
            else:
                break
        
        self.heapList[idx] = data
        self.numOfData += 1


    def HDelete(self):
        retData = self.heapList[1]
        lastElem = self.heapList[self.numOfData]

        parentIdx = 1

        while True:
            childIdx = self.GetHiPriChildIDX(parentIdx)

            if not childIdx:
                break

            if self.comp(lastElem, self.heapList[childIdx]) >= 0:
                break

            self.heapList[parentIdx] = self.heapList[childIdx]
            parentIdx = childIdx

        self.heapList[parentIdx] = lastElem
        self.numOfData -= 1

        return retData
    
def GetParentIDX(idx):
    return idx//2

def GetLChildIDX(idx):
    return idx*2

def GetRChildIDX(idx):
    return GetLChildIDX(idx) + 1

# main

def DataPriorityComp(ch1, ch2):
    return ord(ch2)-ord(ch1) # minheap
    # return ch1-ch2 # maxheap

    # 첫번째 인자 우선 순위 > 두번째 인자 우선순위: 0보다 큰 값 반환
    # 첫번째 인자 우선 순위 < 두번째 인자 우선순위: 0보다 작은 값 반환
    # 첫번째 인자 우선 순위 = 두번째 인자 우선순위: 0 반환

heap = Heap()

heap.HeapInit(pc = DataPriorityComp)

heap.HInsert('A')
heap.HInsert('B')
heap.HInsert('C')
print(heap.HDelete())

heap.HInsert('A')
heap.HInsert('B')
heap.HInsert('C')
print(heap.HDelete())

while not heap.HisEmpty():
    print(heap.HDelete())

② Heapq 라이브러리 기반 구현

heapq 모듈을 import 해서 쉽게 사용할 수 있다.

import heapq

def HeapInit(heap):
    heap = []

def HisEmpty(heap):
    if not heap:
        return True
    else:
        return False

def HInsert(heap, data):
    heapq.heappush(heap, data)

def HDelete(heap):
    if HisEmpty(heap):
        print("Heap Memory Error !")
    else:
        return heapq.heappop(heap)

# main
heap = []

HeapInit(heap)

HInsert(heap, 'A')
HInsert(heap, 'B')
HInsert(heap, 'C')
print(HDelete(heap))

HInsert(heap, 'A')
HInsert(heap, 'B')
HInsert(heap, 'C')
print(HDelete(heap))

while not HisEmpty(heap):
    print(HDelete(heap))

3-3 이진 탐색 트리(Binary Search Tree)

1) 개념

모든 노드가 다음의 조건을 만족하는 이진 트리이다.

왼쪽 서브트리 노드의 키값은 자신의 노드 키 값보다 작아야한다.

오른쪽 서브트리 노드의 키값은 자신의 노드 키값보다 커야 한다.

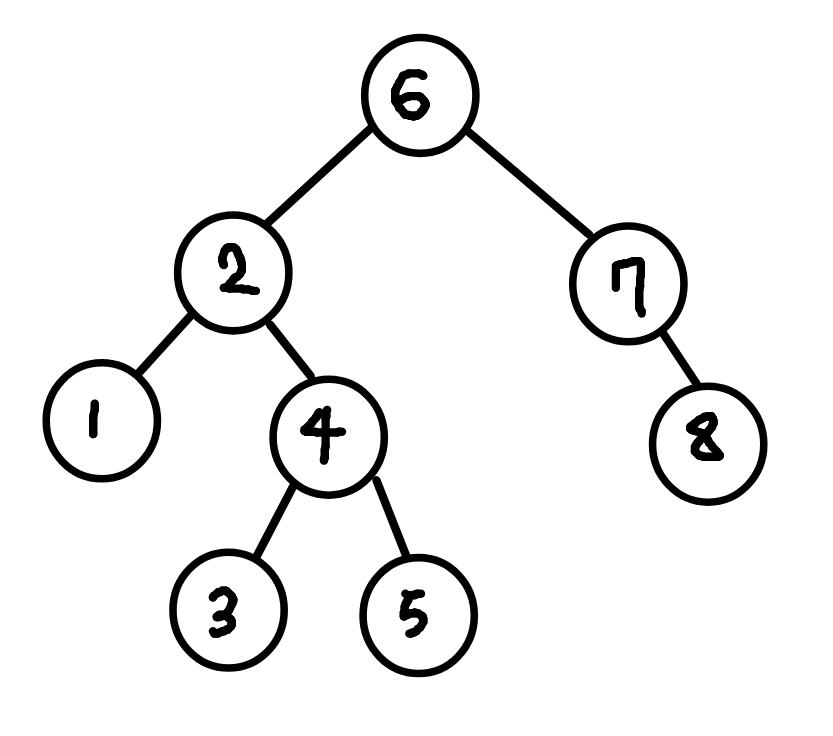
이진 탐색 트리의 특징

중위 순회로 노드값을 오름차순으로 방문 가능(덤프)
빠른 검색 속도
노드 삽입 편리
구조 단순

Search 함수

찾으려는 key값과 루트부터 시작하여 현재 방문중인 노드의 key 값을 비교하며 같아질 때까지 찾아들어간다.

찾으려는 key값 < 방문중인 노드의 key값
→ 왼쪽 자식 방문
찾으려는 key값 > 방문중인 노드의 key값
→ 오른쪽 자식 방문

못 찾았다면 (BST안에 찾으려는 키 값이 존재하지 않다면) None 반환.

Add 함수

search 와 유사하게 추가할 위치를 찾아들어가서 삽입.

Remove 함수

Search와 유사하게 삭제할 노드를 찾아들어간다.

삭제할 노드의 자식 노드가 0개: 삭제할 노드를 가리키는 부모 노드의 포인터를 None으로 바꿔준다. (그냥 삭제)
삭제할 노드의 자식 노드가 1개: 부모노드가 삭제할 노드를 가리키는 방향 그대로 삭제할 노드의 자식을 가리키도록 함. (삭제할 노드 건너뛰기)
삭제할 노드의 자식 노드가 2개)
1. 삭제할 노드의 왼쪽 서브트리에서 가장 오른쪽 노드를 탐색 (가장 큰 노드)
2. 탐색한 노드의 값을 삭제할 노드 값에 복사
3. 탐색한 노드를 삭제
  - 탐색한 노드의 자식이 없는 경우, '삭제할 노드의 자식 노드가 0개'와 동일한 매커니즘.
  - 탐색한 노드의 자식이 1개 있는 경우, '삭제할 노드의 자식 노드가 1개'와 동일한 매커니즘
  - 탐색한 노드의 자식이 2개 있는 경우는 존재하지 않는다. 왼쪽 서브트리의 가장 오른쪽 노드를 탐색한 것이기 때문.

Dump 함수

모든 노드의 키를 오름차순 혹은 내림차순으로 출력하는 함수.

오름차순 출력은 중위순회 방식으로 구현할 수 있다.

Min_key, Max_key 함수

min_key: 가장 왼쪽 노드를 찾아들어가 가장 작은 노드 출력.
max_key: 가장 오른쪽 노드를 찾아들어가 가장 큰 노드 출력.

2) 구현

① Class 기반 구현

from __future__ import annotations
from typing import Any, Type

class Node:
    def __init__(self, key: Any, value: Any, left: Node = None, right: Node = None):
        self.key = key
        self.value = value
        self.left = left
        self.right = right

class BinarySearchTree:
    def __init__(self):
        self.root = None
    
    def search(self, key: Any) -> Any: # Root 부터 시작해서 찾아들어가는 형태.
        p = self.root

        while True:
            if p is None:
                return None
            if key == p.key:
                return p.value
            elif key < p.key: # 찾으려는 key가 현재보다 작으면 왼쪽으로 이동
                p = p.left
            else: 
                p = p.right
    
    def add(self, key: Any, value: Any) -> bool:
        def add_node(node: Node, key: Any, value: Any) -> bool:
            if key == node.key: # 중복 삽입
                return False
            
            elif key < node.key: 
                if node.left is None: # 위치 찾으면 삽입
                    node.left = Node(key, value, None, None)
                else:
                    add_node(node.left, key, value) # 왼쪽 자식으로 이동

            else:
                if node.right is None:
                    node.right = Node(key, value, None, None) # 위치 찾으면 삽입
                else:
                    add_node(node.right, key, value) # 오른쪽 자식으로 이동
            
            return True

        if self.root is None:
            self.root = Node(key, value, None, None)
            return True
        else:
            return add_node(self.root, key, value)
    
    # - 삭제할 노드의 자식 노드가 0개: 삭제할 노드를 가리키는 부모 노드의 포인터를 None으로 바꿔준다. (그냥 삭제)
    # - 삭제할 노드의 자식 노드가 1개: 부모노드가 삭제할 노드를 가리키는 방향 그대로 삭제할 노드의 자식을 가리키도록 함. (삭제할 노드 건너뛰기)
    # - 삭제할 노드의 자식 노드가 2개)
    #   1. 삭제할 노드의 왼쪽 서브트리에서 가장 오른쪽 노드를 탐색 (가장 큰 노드)
    #   2. 탐색한 노드의 값을 삭제할 노드 값에 복사
    #   3. 탐색한 노드를 삭제
    #      3-1) 탐색한 노드의 자식이 없는 경우,  '삭제할 노드의 자식 노드가 0개'와 동일한 매커니즘.
    #      3-2) 탐색한 노드의 자식이 1개 있는 경우, '삭제할 노드의 자식 노드가 1개'와 동일한 매커니즘
    #      3-3) 탐색한 노드의 자식이 2개 있는 경우는 존재하지 않는다. 왼쪽 서브트리의 가장 오른쪽 노드를 탐색한 것이기 때문. 

    def remove(self, key: Any) -> bool:
        p = self.root # 스캔 중인 노드
        parent = None # 스캔 중인 부모 노드
        is_left_child = True # p가 parent의 왼쪽노드인지 

        while True: # 탐색
            if p is None: # 키 값이 존재하지 않음.
                return False  
            
            if key == p.key: # 탐색 성공
                break
            else: # 탐색 과정
                parent = p # 내려가기 전 부모 설정

                if key < p.key: # 왼쪽 자식으로 이동
                    is_left_child = True
                    p = p.left
                else: # 오른쪽 자식으로 이동
                    is_left_child = False
                    p = p.right
        
        if p.left is None: # 왼쪽 자식이 없을 때 (자식의 갯수가 0개 or 1개)
            if p is self.root: # 삭제할 노드가 root 노드이면 오른쪽 자식으로 대체
                self.root = p.right 
            elif is_left_child: # 왼쪽으로 내려왔을 때, 부모의 왼쪽 자식이 오른쪽 자식으로 대체된다.
                parent.left = p.right
            else: # 오른쪽으로 내려왔을 때, 부모의 오른쪽 자식이 오른쪽 자식으로 대체된다.
                parent.right = p.right
        elif p.right is None: # 오른쪽 자식이 없을 때 (자식의 갯수가 0개 or 1개)
            if p is self.root: # 삭제할 노드가 root 노드이면 왼쪽 자식으로 대체 
                self.root = p.left
            elif is_left_child: # 왼쪽으로 내려왔을 때 부모의 왼쪽 자식이 왼쪽 자식으로 대체된다.
                parent.left = p.left
            else:
                parent.right = p.left # 오른쪽으로 내려왔을 때, 부모의 오른쪽 자식이 왼쪽 자식으로 대체된다. 
        else: # 자식의 갯수가 2개인 경우,
            parent = p
            left = p.left # 왼쪽 서브트리로 이동
            is_left_child = True

            while True: # 왼쪽 서브트리 안에서 가장 큰 값을 탐색하는 과정.
                if left.right is None:
                    break

                parent = left
                left = p.right
                is_left_child = False
            
            p.key = left.key
            p.value = left.value

            if is_left_child: # 마지막으로 왼쪽으로 이동했을 때, left의 삭제
                parent.left = left.left # left의 오른쪽 값이 이미 none이고, left는 아직 정해지지 않았기 때문에 이와 같이 일반화 가능.
            else: # 마지막으로 오른쪽으로 이동했을 때, left의 삭제
                parent.right = left.left
            
        return True
    
    def dump(self) -> None: # 덤프(모든 노드를 키의 오름차순으로 출력)
        def print_subtree(node: Node): # node를 루트로 하는 서브트리의 노드를 키의 오름차순으로 출력
            # --> 중위 순회.
            if node is not None: 
                print_subtree(node.left)
                print(node.key, node.value)
                print_subtree(node.right)
        
        def print_subtree_rev(node: Node): # ''' 키의 내림차순 출력
            print_subtree(node.right)
            print(node.key, node.value)
            print_subtree(node.left)
        
        print_subtree(self.root)
    
    def min_key(self) -> Any:
        if self.root is None:
            return None
        
        p = self.root

        while True:
            if p.left is None:
                break

            p = p.left
        
        return p.key
    
    def max_key(self) -> Any:
        if self.root is None:
            return None

        p = self.root

        while True:
            if p.right is None:
                break

            p = p.right
        
        return p.key


bst = BinarySearchTree()

bst.add(1, 1)
bst.add(2, 2)
bst.add(3, 3)
bst.add(4, 4)
bst.add(5, 5)
bst.add(6, 6)
bst.add(7, 7)
bst.add(8, 8)

bst.dump()

print(bst.min_key())
print(bst.max_key())

print(bst.search(2))
bst.remove(2)
print(bst.search(2))

Dictionary로도 구현할 수 있지만, Class 기반 구현과 큰 구현 시간 차이는 아닌 것 같아서 Class 기반으로 구현하는게 더 정확한 구조적 표현을 할 수 있을 거 같다.

3-4 세그먼트 트리(Segment Tree)

1) 개념

부분합을 빠르게 구하고 싶을 때 사용하는 이진트리 자료구조.

기존에 부분합을 구하려면 $O(n)$ 의 시간이 걸린다. 하지만, Segment Tree를 활용하면 미리 구한 부분합을 Binary Tree의 순회로 찾아들어가는 구조이기 때문에 $O(\log n)$ 의 시간만에 원하는 부분합을 구할 수 있다.

build, query, update 3개 함수로 구현하고, 모두 재귀를 활용한 분할정복 기법으로 구현할 수 있다.

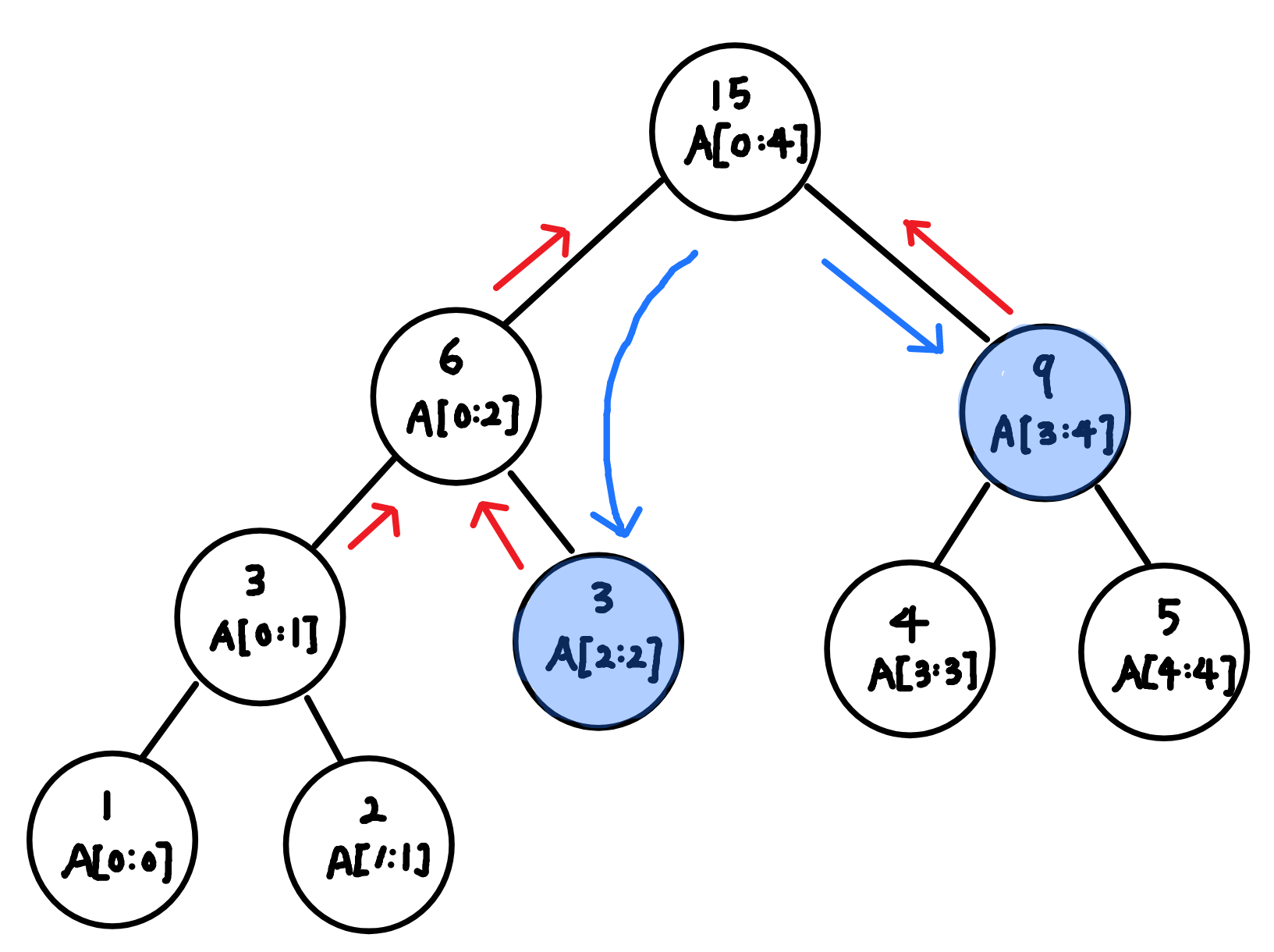
배열 A([1, 2, 3, 4, 5])에 대한 구간 합을 구하고자 할 때, Tree의 Leaf 노드들에 A 배열의 원소들이 하나씩 위치하게끔 구현하고, 각 노드들의 왼쪽 자식과 오른쪽 자식을 합하여 전체적인 Segment Tree를 완성하게 된다.

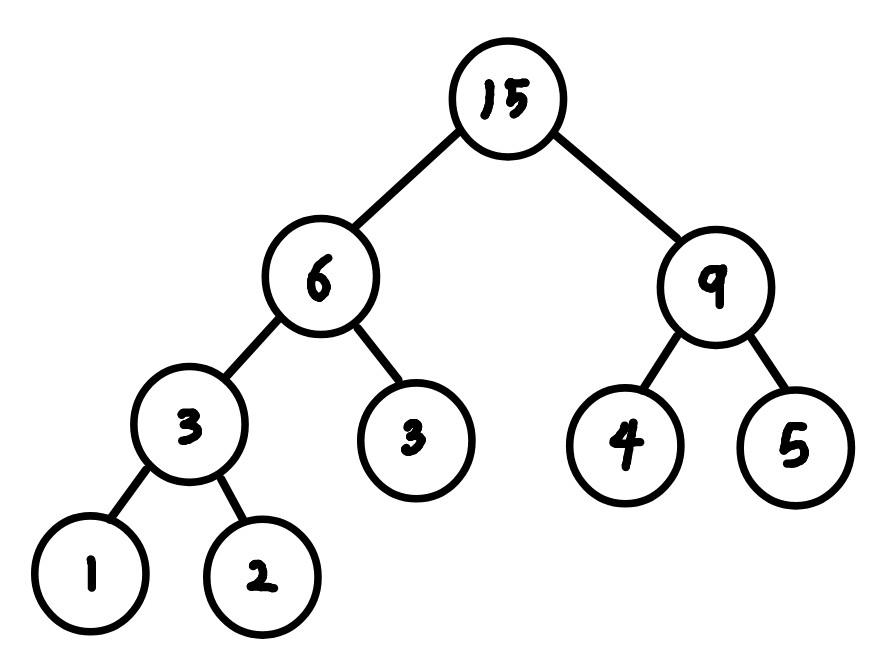
Build

Leaf node, A 배열의 각 원소 저장.
Internal Node, 자식 노드의 합 저장.

Query

각 노드의 범위가 구하려는 범위 밖에 있는 경우
: return 0
각 노드의 범위가 구하려는 범위를 완전 포함하는 경우
: return tree[node] (범위의 부분 합을 이미 담고 있음.)
각 노드의 범위가 구하려는 범위를 일부 포함하는 경우
: 자식 노드로 진입해 다시 시행한 값을 반환. (범위를 좁히는 과정)

2, 4

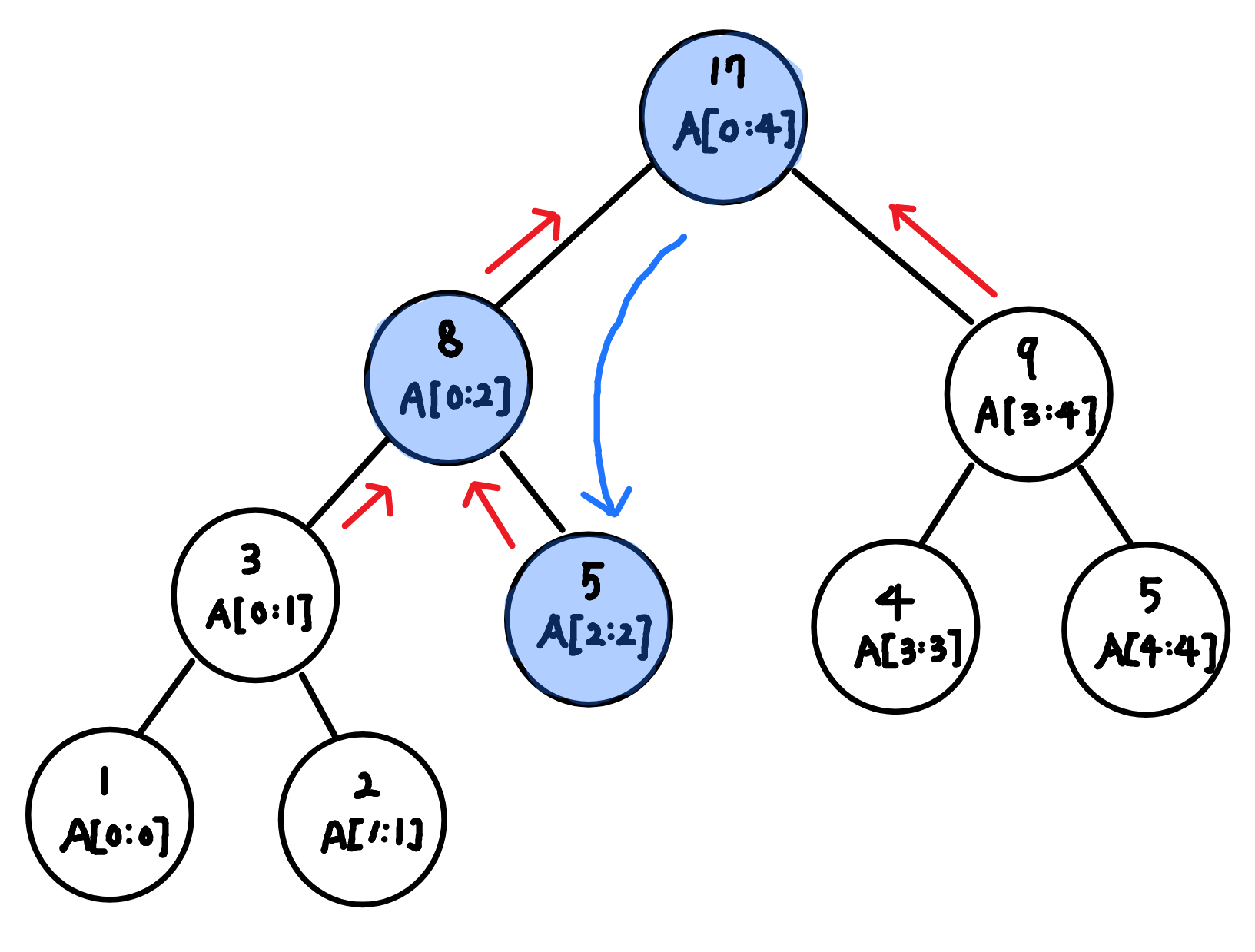
Update

A 배열의 index번째 값을 val로 바꿔서 Segment Tree의 일부가 변경될 때 사용한다.

바꾸려는 값이 좌측 자식 노드인지, 우측 자식노드인지 판단하고 거기로 계속 재귀적으로 내려간다. 그러다가, 리프노드(바꾸고 싶은 값(index))까지 도달시 val로 변경하고, conquer 방식으로 위로 올라가며 자식 노드의 합을 계산해 영향 받는 노드의 값을 업데이트 한다.

2) 구현

① 배열 기반 구현

# top-down, 분할정복 기법
def build(node, start, end): 
    if start == end: # leaf node
        tree[node] = a[start]
        return

    mid = (start + end) // 2
    build(2*node, start, mid) # left child
    build(2*node+1, mid+1, end)

    tree[node] = tree[node*2] + tree[node*2+1]
    return

def query(node, start, end, left, right):
    if right < start or end < left: # out of range
        return 0
    if left <= start and end <= right: # 모두 범위 안에 있는 경우
        return tree[node]
    
    # 일부만 범위에 포함되는 경우
    mid = (start + end) // 2

    left_child = query(node*2, start, mid, left, right)
    right_child = query(node*2+1 , mid+1, end, left, right)

    return left_child + right_child

def update(node, start, end, index, val): 
    if start == end: # leaf node
        tree[node] = val
        return

    mid = (start + end) // 2

    if start <= index <= mid:
        update(node*2, start, mid, index, val)
    else:
        update(node*2+1, mid+1, end, index, val)
    
    tree[node] = tree[node*2] + tree[node*2+1]
    return 

a = [1, 2, 3, 4, 5]

n = len(a)
tree_size = 4*n # 완전 이진 트리일때도 충분한 크기 정의 위함.

tree = [0] * tree_size

start_node = 1
start = 0
end = n-1

build(start_node, start, end)
print(tree)

print(query(start_node, start, end, 2, 4))

update(start_node, start, end, 2, 5)
print(tree)

3-5 그래프(Graph)

1) 개념

정점(Vertex)
간선(Edge)

방향 그래프 (Directed Graph)
무방향 그래프 (Undirected Graph)

가중치 그래프 (Weight Graph)

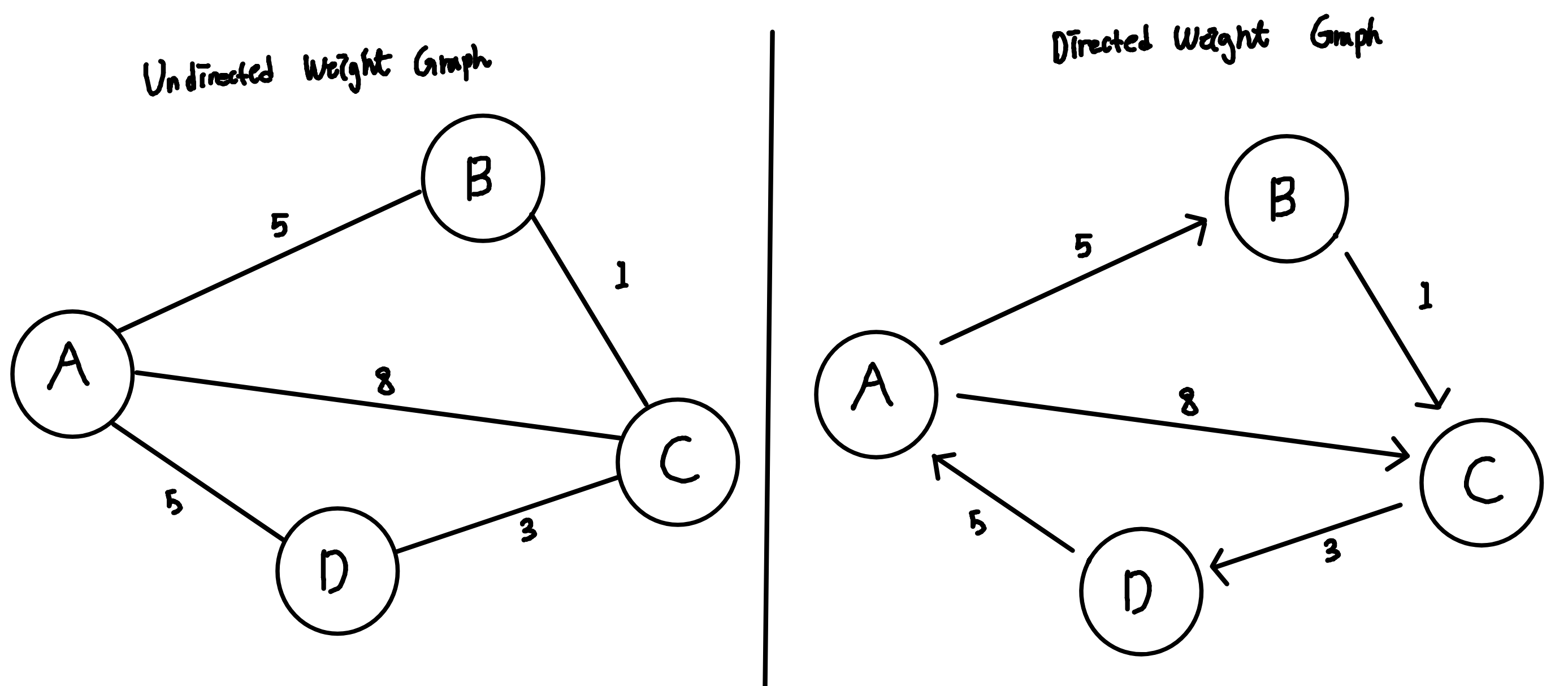
2) 구현

① 인접 행렬 기반 구현

v = 10 # vertex

connection = [[1, 2], [1, 9], [2, 3], [3, 4], [3, 5], [7, 8]]

graph = [[0 for i in range(v+1)] for j in range(v+1)] # 인접 행렬 기반

for start, end in connection:
    graph[start][end] = 1
    # graph[end][start] = 1 # undirected graph

print(graph)

② 인접 리스트 기반 구현

v = 10 # vertex

connection = [[1, 2], [1, 9], [2, 3], [3, 4], [3, 5], [7, 8]]

graph = {} # 인접 리스트 기반
visited = [False] * (v+1)

for start, end in connection:
    graph[start] = []
    # graph[end] = [] # undirected graph

for start, end in connection:
    graph[start].append(end)
    # graph[end].append(start) # undirected graph

print(graph)

3-6 해쉬 테이블 (Hash Table)

1) 개념

해시 함수에 의해 계산된 위치에 값을 저장하는 테이블 자료구조.

시간복잡도

	Best	Worst
탐색	$O(1)$	O(n)
삽입	$O(1)$	O(n)
삭제	$O(1)$	O(n)

공간을 이용해 시간 효율성을 높이는 대표적인 전략이다.

해시 테이블은 M개의 버킷을 가지고, 이 버킷은 여러 개의 슬롯을 가진다. 슬롯을 하나라고 하면, 버킷이 충분하지 않을 때, 서로 다른 키가 해시함수에 의해 같은 주소로 계산되는 상황이 발생한다. 이를 충돌(collision)이라고 하며, 이때의 키들을 동의어(synonym)라고 한다.

어떤 버킷에 슬롯 수보다 많은 충돌이 발생하면 그 버킷에 저장할 수 없게 되고, 이를 오버플로(overflow)라고 한다.

따라서, 테이블의 크기를 적절히 줄이고, 해시 함수를 이용해 주소가 가능한한 전체 테이블에 골고루 배분 될 수 있도록 해야한다.

해시 함수로 계산된 버킷에 빈 슬롯이 없으면 그 다음 버킷들을 순차적으로 조사하여 빈 슬롯이 있는지 찾는다. 이를 조사(probing)라고 한다.

선형 조사법과 체이닝은 충돌을 해결하기 위해 사용하는 대표적인 방법이다.

① 선형 조사법 (Linear Probing)

삽입
충돌 발생시, 한칸씩 오른쪽으로 이동해서 다시 시도해보면서 빈 공간을 찾는다. 오른쪽 끝에 닿으면 처음으로 돌아가서 다시 시도한다.
탐색
삽입과 유사하게 해시주소를 계산하고, 다음 버킷을 검사하며 값을 비교한다. 그러다가 없는 버킷을 만나거나, 모든 버킷을 검사하면 탐색 실패이다.
삭제
삭제도 탐색과 마찬가지로, 다음 버킷을 탐색하여 값을 비교하고 삭제한다. 하지만, 항목이 아에 없던 것처럼 된다면 탐색이 불가해질 수 있기 때문에 아에 사용되지 않았던 버킷과 삭제되어 비어있는 버킷을 구분한다.

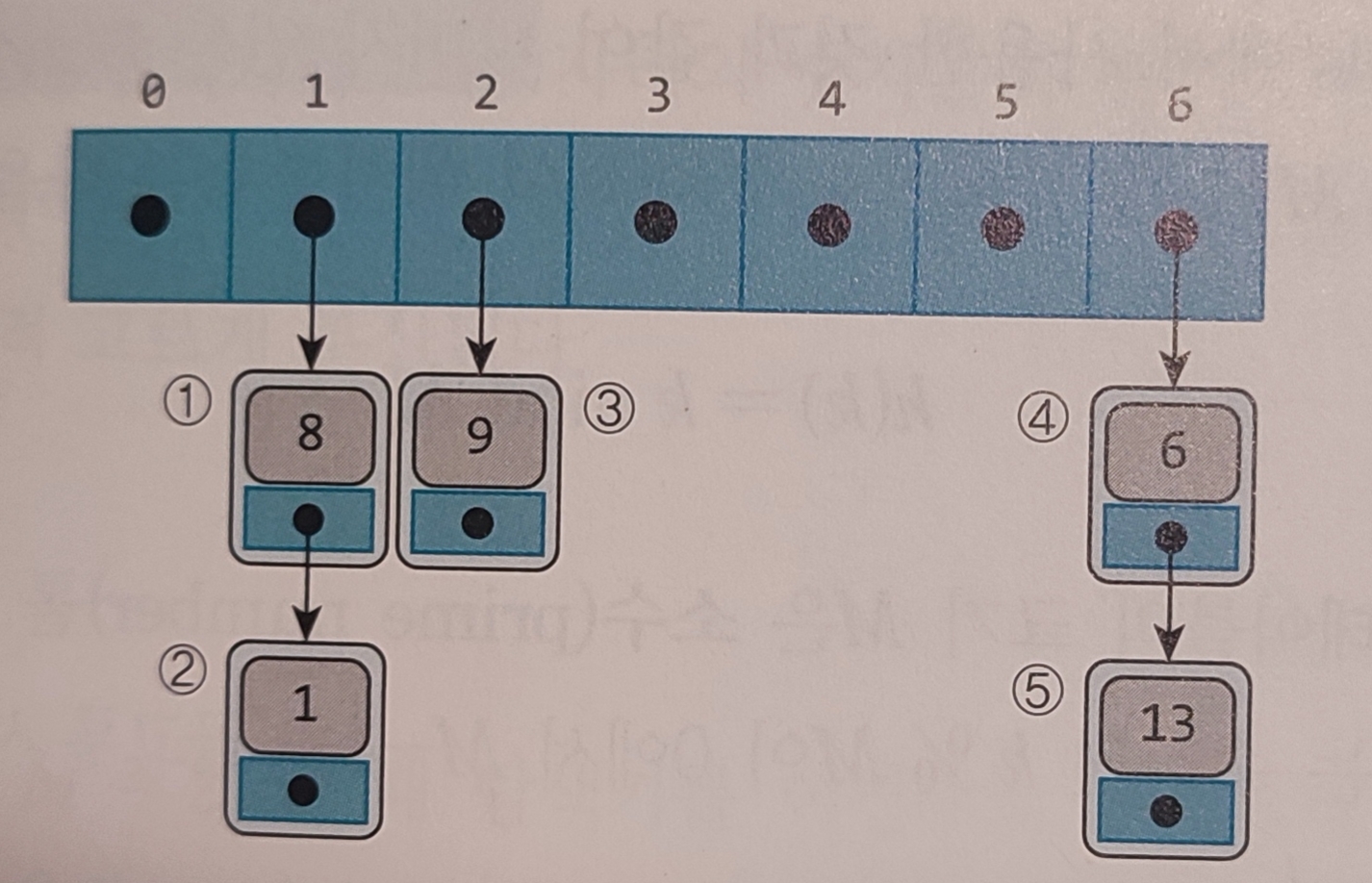
② 체이닝 (Chaining)

하나의 버킷에 여러 개의 레코드를 저장할 수 있도록 Linked List 기반으로 구현한다.

해시 함수 (Hash Function)

키값에서 저장될 위치를 계산하는 함수.
탐색키를 입력받아 해시 주소를 계산한다.

대표적으로 나머지 연산 %(modular)를 이용하는 방법인 '제산 함수'가 사용 된다.

$h(k) = k \mod M$

2) 구현

① 선형 조사법을 적용한 구현

def hashFn(key):
    return key % M

def insert(key):
    i = hashFn(key)
    count = M

    while count > 0:
        if table[i] == None:
            break

        i = (i+1) % M # 오른쪽 바운더리에 닿으면 되돌아가도록 / 1씩 증가
        count -= 1
    
    if count > 0:
        table[i] = key

def delete(key):
    i = hashFn(key)
    count = M

    while count > 0:
        if table[i] == key:
            table[i] = -1
            return 

        if table[i] == None:
            return 
        
        i = (i+1) % M
        count -= 1

def search(key):
    i = hashFn(key)
    count = M

    while count > 0:
        if table[i] == None:
            return None
        if table[i] == key:
            return i
        i  = (i+1) % M
        count -= 1
    
    return None

M = 13
table = [None] * M

data = [45, 27, 88, 9, 71, 60, 46, 38, 24]

for d in data:
    print("h(%2d) = %2d"%(d, hashFn(d)), end=' ')
    insert(d)
    print(table)

print("46탐색 --> 인덱스 번호:", search(46))
print("39탐색 --> 인덱스 번호:", search(39))
print("60 삭제 -->", end='')
delete(60)
print(table)

② 체이닝을 적용한 구현

def hashFn(key):
    return key % M

class Node:
    def __init__(self, data, link = None):
        self.data = data
        self.link = link

def insert(key):
    k = hashFn(key)
    n = Node(key)
    n.link = table[k]
    table[k] = n

def printTable():
    for i in range(M):
        n = table[i]

        if n != None:
            print("[%2d]" %i, end=' ')

            while n is not None:
                print(n.data, end=' ')
                n = n.link
            
            print()

def search(key):
    k = hashFn(key)
    n = table[k]

    while n is not None:
        if n.data == key:
            return n.data
        
        n = n.link

    return None

def delete(key):
    k = hashFn(key)
    n = table[k]

    before = None

    while n is not None:
        if n.data == key:
            if before == None:
                table[k] = n.link
            else:
                before.link = n.link
            
            return 
        
        before = n
        n = n.link

M = 13
table = [None] * M


data = [45, 27, 88, 9, 71, 60, 46, 38, 24]

for d in data:
    insert(d)

printTable()

print("46탐색 --> 인덱스 번호:", search(46))
print("39탐색 --> 인덱스 번호:", search(39))

print("60 삭제 -->", end='')
delete(60)

printTable()

김두현

HYU ERICA 23 ICT융합학부 미디어테크놀로지전공 김두현

이전 포스트

[CS] Python 알고리즘 정리

다음 포스트

[CS] Python 자료구조 정리

Computer Science Study

참고 서적

I. 자료구조의 분류

II. 선형 자료구조

2-1 단순 연결 리스트(Linked List)

1) 개념

2) ADT

def ListInit(self):

def LInsert(self, data):

def LFirst(self):

def LNext(self):

def LRemove(self):

def LCount(self):

3) 구현

2-2 원형 연결 리스트(Circular Linked List)

1) 개념

2) 구현

① 연결 리스트 기반 구현

② 배열 기반 구현

2-3 양방향 연결 리스트(Doubly Linked List)

1) 개념

2) 구현

① 연결 리스트 기반 구현

2-4 스택(Stack)

1) 개념

2) ADT

def StackInit(self):

def SIsEmpty(self):

def SPush(self, data):

def SPop(self):

def SPeek(self):

3) 구현

① 연결 리스트 기반 구현

② 배열 기반 구현

2-5 큐(Queue)

1) 개념

2) ADT

def QueueInit(self):

def QIsEmpty(self):

def Enqueue(self, data):

def Dequeue(self):

def QPeek(self):

3) 구현

① 연결 리스트 기반 구현

② Deque 라이브러리 기반 구현

2-6 덱(Deque)

1) 개념

2) ADT

def dequeInit(Deque):

def dequeIsEmpty(Deque):

def dequeAddFirst(Deque, data):

def dequeAddLast(Deque, data):

def dequeRemoveFirst(Deque):

def dequeRemoveLast(Deque):

def dequeGetFirst(Deque):

def dequeGetLast(Deque):

3) 구현

① 양방향 연결 리스트 기반 구현

② Deque 라이브러리 기반 구현

2-7 우선순위 큐(Priorty Queue)

1) 개념

2) ADT

def PQueueInit(self, pc):

def PQIsEmpty(self):

def PEnqueue(self, data):

def PDequeue(self):

3) 구현

① 힙 기반 구현

② Heapq 라이브러리 기반 구현

III. 비선형 자료구조

3-1 이진 트리(Binary Tree)

1) 개념

트리의 용어

형제 노드의 순서 관계에 따른 트리 분류

이진 트리 분류 용어

트리의 순회

2) ADT

def MakeBTreeNode(self):

def GetData(self):