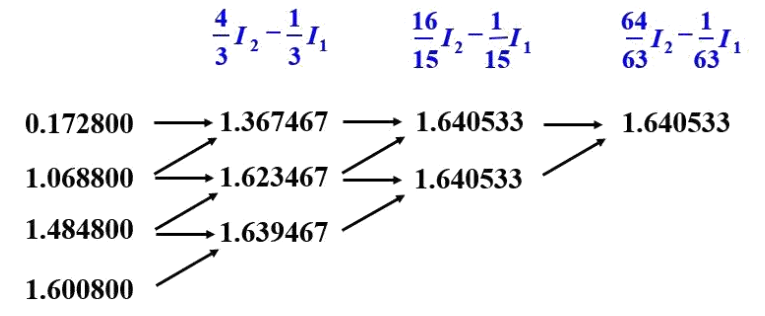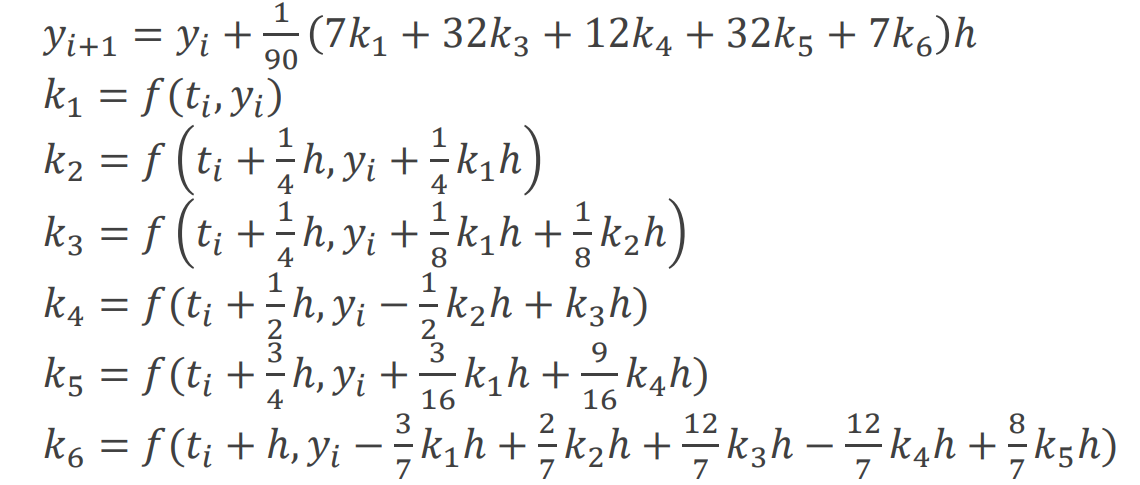CHAPTER 13 고유치(Eigenvalue)
13-1 고유치와 고유벡터
A x = λ x Ax = \lambda x A x = λ x
벡터 x가 존재할 때, 스칼라 λ \lambda λ
( A − λ I ) x = 0 (A-\lambda I)x = 0 ( A − λ I ) x = 0
det ( A − λ I ) = 0 \det(A-\lambda I) = 0 det ( A − λ I ) = 0
구한 고유치를 아래의 원래 식에 대입하여 방정식을 풀고,( A − λ I ) x = 0 (A-\lambda I)x = 0 ( A − λ I ) x = 0
x가 (n x 1)의 열 벡터이고, 방정식을 만족하는 임의의 x값들을 찾으면 그것이 각 고유치에 만족하는 고유벡터이다.
import numpy as np
A = np.array([[40., -20., 0.],
[-20., 40., -20],
[0., -20., 40.]])
e = np.linalg.eigvals(A)
print("Eigenvalues:", e)
e, v = np.linalg.eig(A)
print("Eigenvalues:", e)
print("Eigenvector:", v)13-2 멱 방법(The Power Method)
가장 크거나 지배적인 고유치를 구하기 위해 사용한다.
초기 고유벡터를 가정한다.X 1 = [ 1 1 1 ] , λ 1 = 1 X_1 = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}, \lambda_1 = 1 X 1 = ⎣ ⎢ ⎡ 1 1 1 ⎦ ⎥ ⎤ , λ 1 = 1
선형 방정식에 예측 고유벡터를 근으로 해서 계산A X 1 = b AX_1 = b A X 1 = b
가정한 X를 가지고 새로운 b를 구해 개선된 Eigen Vetor와 Eigen Value 값 도출b = [ 20 0 20 ] → X 2 = [ 1 0 1 ] , λ 2 = 20 b = \begin{bmatrix} 20 \\ 0 \\ 20 \end{bmatrix} \rarr X_2 = \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix}, \lambda_2 = 20 b = ⎣ ⎢ ⎡ 2 0 0 2 0 ⎦ ⎥ ⎤ → X 2 = ⎣ ⎢ ⎡ 1 0 1 ⎦ ⎥ ⎤ , λ 2 = 2 0
ϵ a = ∣ 현재근사고유치 − 이전근사고유치 현재근사고유치 ∣ × 100 \epsilon_a = |{현재 근사 고유치 - 이전 근사 고유치 \over 현재 근사 고유치} | \times 100 ϵ a = ∣ 현 재 근 사 고 유 치 현 재 근 사 고 유 치 − 이 전 근 사 고 유 치 ∣ × 1 0 0 ϵ s \epsilon_s ϵ s
CHAPTER 14 선형회귀분석 (Linear Regression)
14-0 통계 기초
y ˉ \bar y y ˉ y ~ \tilde y y ~
S S T = Σ ( y i − y ˉ ) 2 SS_T = \Sigma(y_i - \bar y)^2 S S T = Σ ( y i − y ˉ ) 2
편차 s y = S S T n − 1 s_y = \sqrt {SS_T \over n-1} s y = n − 1 S S T s y 2 = S S T n − 1 s_y^2 = {SS_T \over n-1} s y 2 = n − 1 S S T
변동계수 (Coefficient of Variation (c.v.)): 데이터의 변동성 지표c . v . = s y y ˉ 100 % c.v. = {s_y\over\bar y} 100\% c . v . = y ˉ s y 1 0 0 %
정규분포의 확률 밀도 함수 수식f ( y ) = 1 2 π σ 2 e − ( y − μ ) 2 2 σ 2 f(y) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{(y - \mu)^2}{2\sigma^2}} f ( y ) = 2 π σ 2 1 e − 2 σ 2 ( y − μ ) 2
정규분포에서 적분시 그 구간에 속할 확률을 구하는 것.f ( μ ) = 1 σ 2 π f(\mu) = \frac{1}{\sigma \sqrt{2\pi}} f ( μ ) = σ 2 π 1
표준정규분포(Standard Normal Distribution)z = y − μ σ z = \frac{y - \mu}{\sigma} z = σ y − μ f ( z ) = 1 2 π e − z 2 2 f(z) = \frac{1}{\sqrt{2\pi}} e^{-\frac{z^2}{2}} f ( z ) = 2 π 1 e − 2 z 2
Normal Probability Rule
14-1 선형회귀분석
1) 곡선접합(Curve Fitting)
주어진 n개의 점 데이터 (x1, y1), ..., (xn, yn)에 대한 곡선 접합 방법
보간법(Interpolation)
주어진 점 데이터가 정확한 값이어서 모든 점을 통과하는 곡선식을 유도한다.
Linear Interpolation
Curvilinear Interpolation
회귀분석법
주어진 점 데이터가 정확하지 않을 수 있어서 점들의 경향을 곡선식으로 유도한다.
Least-Sqaures Regression
2) 선형회귀분석 (Linear Least-Sqaures Regression)
최소자승법(Least Sqaure Method; LSM)을 이용한 편차를 최소화한 선형함수.
* 자승: 제곱
선형회귀분석 과정
적합 회귀 직선식 가정: g ( x ) = a 0 + a 1 x g(x) = a_0 + a_1x g ( x ) = a 0 + a 1 x
잔차 r i = y i − g ( x i ) = y i − ( a 0 + a 1 x i ) r_i = y_i - g(x_i) = y_i - (a_0 + a_1x_i) r i = y i − g ( x i ) = y i − ( a 0 + a 1 x i )
잔차의 제곱합 S r = Σ i n ( r i ) 2 = Σ i n ( y i − a 0 − a 1 x i ) 2 S_r = \Sigma^n_i(r_i)^2 = \Sigma^n_i(y_i - a_0 - a_1x_i)^2 S r = Σ i n ( r i ) 2 = Σ i n ( y i − a 0 − a 1 x i ) 2
S r S_r S r a 0 , a 1 a_0, a_1 a 0 , a 1
* 잔차(residual): 회귀 분석에서 관측값에서 회귀식에 의한 추정량을 뺀 값.
S r S_r S r a 0 , a 1 a_0, a_1 a 0 , a 1 ∂ S r ∂ a 0 = 0 , ∂ S r ∂ a 1 = 0 {\partial S_r \over \partial a_0} = 0, {\partial S_r \over \partial a_1} = 0 ∂ a 0 ∂ S r = 0 , ∂ a 1 ∂ S r = 0
∂ S r ∂ a 0 = − 2 Σ i n ( y i − a 0 − a 1 x i ) = 0 {\partial S_r \over \partial a_0} = -2\Sigma^n_i(y_i - a_0 - a_1x_i) =0 ∂ a 0 ∂ S r = − 2 Σ i n ( y i − a 0 − a 1 x i ) = 0 Σ y i − n a 0 − a 1 Σ x i = 0 \Sigma y_i - na_0 - a_1\Sigma x_i = 0 Σ y i − n a 0 − a 1 Σ x i = 0 n 0 ( a 0 ) + ( Σ x i ) ( a 1 ) = Σ y i n_0(a_0) + (\Sigma x_i)(a_1) = \Sigma y_i n 0 ( a 0 ) + ( Σ x i ) ( a 1 ) = Σ y i
∂ S r ∂ a 1 = − 2 Σ i n x i ( y i − a 0 − a 1 x i ) = 0 {\partial S_r \over \partial a_1} = -2\Sigma^n_ix_i(y_i - a_0 - a_1x_i) = 0 ∂ a 1 ∂ S r = − 2 Σ i n x i ( y i − a 0 − a 1 x i ) = 0 Σ x i y i − a 0 Σ x i − a 1 Σ x i 2 = 0 \Sigma x_iy_i - a_0 \Sigma x_i - a_1\Sigma x_i^2 = 0 Σ x i y i − a 0 Σ x i − a 1 Σ x i 2 = 0 ( Σ x i ) ( a 0 ) + ( Σ x i 2 ) ( a 1 ) = Σ x i y i (\Sigma x_i)(a_0) + (\Sigma x^2_i)(a_1) = \Sigma x_iy_i ( Σ x i ) ( a 0 ) + ( Σ x i 2 ) ( a 1 ) = Σ x i y i
두 수식을 연립하여 a0와 a1 해를 구한다. (Crammer's Rule, Gauss Elimination, ...)
오차의 정량화 (결정 계수)
구한 회귀 직선이 얼마나 잘 경향을 잘 나타내는지 정도를 측정하는 방법.
선형회귀직선에 대한 잔차의 제곱합S r = Σ i n ( r i ) 2 = Σ i n ( y i − a 0 − a 1 x i ) 2 S_r = \Sigma^n_i(r_i)^2 = \Sigma^n_i(y_i - a_0 - a_1x_i)^2 S r = Σ i n ( r i ) 2 = Σ i n ( y i − a 0 − a 1 x i ) 2
평균값에 대한 잔차의 제곱합S t = Σ i n ( y i − y ˉ ) 2 S_t = \Sigma ^n_i (y_i - \bar y)^2 S t = Σ i n ( y i − y ˉ ) 2
결정 계수 (Coefficient of Determination)0 ≤ r 2 = S t − S r S t ≤ 1 0 \leq r^2 = {S_t - S_r \over S_t} \leq 1 0 ≤ r 2 = S t S t − S r ≤ 1
0이라면 S r = S t S_r = S_t S r = S t S r = 0 S_r = 0 S r = 0
import numpy as np
import matplotlib.pyplot as plt
def strlinregr(x, y):
n = len(x)
if len(y) != n:
return 'x and y must be of same length'
sumx = np.sum(x)
sumy = np.sum(y)
sumxy = np.sum(x*y)
sumsqx = np.sum(x**2)
avgy = np.average(y)
A = np.array([[n, sumx],
[sumx, sumsqx]])
b = np.array([[sumy],
[sumxy]])
[a0], [a1] = np.linalg.solve(A, b)
sr = np.sum((y-(a0 + a1*x))**2)
st = np.sum((y-avgy)**2)
rsq = (st-sr)/st
return a0, a1, rsq
x = np.array([10., 20., 30., 40., 50., 60., 70., 80.])
y = np.array([25.,70., 380., 550., 610., 1220., 830., 1450.])
a0, a1, rsq = strlinregr(x, y)
print("Intercept = %.2f" %a0)
print("Slope = %.2f" %a1)
print("R-squared = %.2f" %rsq)
# Graphical Displays
xline = np.linspace(0, 90, 10)
yline = a0 + a1*xline
plt.scatter(x, y, c='k')
plt.plot(xline, yline, c='k')
plt.grid()
plt.xlabel('x')
plt.ylabel('y')
plt.show()14-2 비선형방정식의 선형회귀분석 (Linear Regression for Nonlinear Relationships)
1) 비선형 방정식의 선형화
지수 방정식
y = α 1 e β 1 x y = \alpha_1 e^{\beta_1x} y = α 1 e β 1 x ln y = ln α 1 + β 1 x \ln y= \ln\alpha_1 + \beta_1x ln y = ln α 1 + β 1 x
Y = ln y Y = \ln y Y = ln y A 0 = ln α 1 A_0 = \ln\alpha_1 A 0 = ln α 1 A 1 = β 1 A1= \beta_1 A 1 = β 1 X = x X= x X = x
Y = A 0 + A 1 X Y = A_0 + A_1X Y = A 0 + A 1 X
멱 방정식
y = α 2 x β 2 y = \alpha_2x^{\beta_2} y = α 2 x β 2 ln y = ln α 2 + β 2 ln x \ln y = \ln\alpha_2 + \beta_2\ln x ln y = ln α 2 + β 2 ln x
Y = ln y Y = \ln y Y = ln y A 0 = ln α 2 A_0 = \ln\alpha_2 A 0 = ln α 2 A 1 = β 2 A1= \beta_2 A 1 = β 2 X = ln x X = \ln x X = ln x
Y = A 0 + A 1 X Y = A_0 + A_1X Y = A 0 + A 1 X
포화-성장률 방정식
y = α 3 x β 3 + x y = {\alpha_3 x \over \beta_3+x} y = β 3 + x α 3 x 1 y = β 3 α 3 x + x α 3 x = 1 α 3 + β 3 α 3 1 x {1 \over y} = {\beta_3 \over \alpha_3 x} + {x \over \alpha_3 x} = {1 \over \alpha_3} + {\beta_3 \over \alpha_3}{1 \over x} y 1 = α 3 x β 3 + α 3 x x = α 3 1 + α 3 β 3 x 1
Y = 1 y Y = {1 \over y} Y = y 1 A 0 = 1 α 3 A_0 = {1 \over \alpha_3} A 0 = α 3 1 A 1 = β 3 α 3 A_1 = {\beta_3 \over \alpha_3} A 1 = α 3 β 3 X = 1 x X = {1 \over x} X = x 1
Y = A 0 + A 1 X Y = A_0 + A_1X Y = A 0 + A 1 X
CHAPTER 15 일반적인 선형 및 비선형회귀분석 (General Linear Least-Sqaures and Nonlinear Regression)
15-1 다항식 회귀분석 (Polynomial Regression)
m차 다항식으로 n개 데이터를 적합시키는 경우g ( x ) = a 0 + a 1 x + a 2 x 2 + . . . + a m x m g(x) = a_0 + a_1x + a_2x^2 + ... + a_mx^m g ( x ) = a 0 + a 1 x + a 2 x 2 + . . . + a m x m
잔차 r i = y i − g ( x i ) r_i = y_i - g(x_i) r i = y i − g ( x i ) S r = Σ i n ( r i ) 2 S_r= \Sigma^n_i (r_i)^2 S r = Σ i n ( r i ) 2 Σ i n ( y i − a 0 − a 1 x − a 2 x 2 − . . . − a m x m ) 2 \Sigma^n_i(y_i - a_0 - a_1x - a_2x^2 - ... - a_mx^m)^2 Σ i n ( y i − a 0 − a 1 x − a 2 x 2 − . . . − a m x m ) 2
S r S_r S r a 0 a_0 a 0 a m a_m a m ∂ S r ∂ a k = 0 {\partial S_r \over \partial a_k} = 0 ∂ a k ∂ S r = 0
→ Σ j = 0 m ( Σ i = 1 n x i j + k ) a j = Σ i = 1 n x i k y i \Sigma^m_{j=0} (\Sigma^n_{i=1} x_i^{j+k})a_j = \Sigma^n_{i=1}x^k_iy_i Σ j = 0 m ( Σ i = 1 n x i j + k ) a j = Σ i = 1 n x i k y i
이것을 행렬로 나타내면,
[ n Σ x i Σ x i 2 . . . Σ x i m Σ x i Σ x i 2 Σ x i 3 . . . Σ x i m + 1 . . . Σ x i m Σ x i m + 1 Σ x i m + 2 . . . Σ x i 2 m ] \begin{bmatrix} n & \Sigma x_i & \Sigma x_i^2 & ... &\Sigma x_i^m \ \\ \Sigma x_i & \Sigma x_i^2 & \Sigma x_i^3 & ... &\Sigma x_i^{m+1} \\ & & . \\ & & . \\ & & . \\ \Sigma x_i^m & \Sigma x_i^{m+1} & \Sigma x_i^{m+2} & ... &\Sigma x_i^{2m} \\ \end{bmatrix} ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ n Σ x i Σ x i m Σ x i Σ x i 2 Σ x i m + 1 Σ x i 2 Σ x i 3 . . . Σ x i m + 2 . . . . . . . . . Σ x i m Σ x i m + 1 Σ x i 2 m ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ [ a 0 a 1 . . . a m ] \begin{bmatrix} a_0 \\ a_1\\ . \\ . \\ . \\ a_m \\ \end{bmatrix} ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ a 0 a 1 . . . a m ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ [ Σ y i Σ x i y i . . . Σ x i m y i ] \begin{bmatrix} \Sigma y_i \\ \Sigma x_iy_i\\ . \\ . \\ . \\ \Sigma x_i^my_i \\ \end{bmatrix} ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ Σ y i Σ x i y i . . . Σ x i m y i ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
( m + 1 ) × ( m + 1 ) (m+1) \times (m+1) ( m + 1 ) × ( m + 1 ) a 0 a_0 a 0 a m a_m a m
s e = S S E n − ( m + 1 ) s_e = \sqrt{SS_E\over n-(m+1)} s e = n − ( m + 1 ) S S E
import numpy as np
def ployregr(x, y, m):
n = len(x)
A = np.zeros((m+1, m+1))
b = np.zeros((m+1, 1))
for k in range(m+1):
for j in range(m+1):
A[k, j] = np.sum(x**(j+k))
b[k, 0] = np.sum(x**k * y)
a = np.linalg.solve(A, b).flatten()
poly_func = np.poly1d(a[::-1])
y_pred = poly_func(x)
y_avg = np.average(y)
sr = np.sum((y-y_pred)**2)
st = np.sum((y-y_avg)**2)
r_square = (st-sr)/st
print(a)
print("%.5f" %r_square)
x = np.array([0., 4.44, 10., 15.56, 21.11, 26.67, 32.22, 37.78, 48.89, 60., 71.11, 82.22, 93.33])
y = np.array([1.794, 1.546, 1.31, 1.129, 0.982, 0.862, 0.764, 0.682, 0.559, 0.47, 0.401, 0.347, 0.305])
ployregr(x, y, 2)15-2 다중 선형회귀분석(Multiple Linear Regression)
y가 2개 이상의 독립변수이고, 선형일 때 사용한다.
독립변수가 x1, x2 일때의 선형식. (x3, x4, ... 로 확장 가능)g ( x ) = a 0 + a 1 x 1 + a 2 x 2 g(x) = a_0 + a_1x_1 + a_2x_2 g ( x ) = a 0 + a 1 x 1 + a 2 x 2 r i ( x 1 , x 2 ) = y i − g ( x 1 , i , x 2 , i ) r_i(x_1, x_2) = y_i - g(x_{1,i}, x_{2, i}) r i ( x 1 , x 2 ) = y i − g ( x 1 , i , x 2 , i ) S r = Σ i n ( r i ) 2 = Σ i n ( y i − a 0 − a 1 x 1 , i − a 2 x 2 , i ) 2 Sr = \Sigma^n_i(r_i)^2 = \Sigma^n_i(y_i - a_0 - a_1x_{1,i} - a_2x_{2,i})^2 S r = Σ i n ( r i ) 2 = Σ i n ( y i − a 0 − a 1 x 1 , i − a 2 x 2 , i ) 2
S r S_r S r a 0 , a 1 , a 2 a_0, a_1, a_2 a 0 , a 1 , a 2 ∂ S r ∂ a i = 0 {\partial S_r \over \partial a_i} = 0 ∂ a i ∂ S r = 0
[ n Σ x 1 , i Σ x 2 , i Σ x 1 , i Σ x 1 , i 2 Σ x 1 , i x 2 , i Σ x 2 , i Σ x 1 , i x 2 , i Σ x 2 , i 2 ] [ a 0 a 1 a 2 ] = [ Σ y i Σ x 1 , i y i Σ x 2 , i y i ] \begin{bmatrix} n & \Sigma x_{1, i} & \Sigma x_{2, i} \\ \Sigma x_{1, i} & \Sigma x_{1, i}^2 & \Sigma x_{1, i}x_{2, i} \\ \Sigma x_{2, i} & \Sigma x_{1, i}x_{2, i} & \Sigma x_{2, i}^2 \\ \end{bmatrix} \begin{bmatrix} a_0 \\ a_1\\ a_2 \\ \end{bmatrix} = \begin{bmatrix} \Sigma y_i \\ \Sigma x_{1,i}y_i\\ \Sigma x_{2,i}y_i \\ \end{bmatrix} ⎣ ⎢ ⎡ n Σ x 1 , i Σ x 2 , i Σ x 1 , i Σ x 1 , i 2 Σ x 1 , i x 2 , i Σ x 2 , i Σ x 1 , i x 2 , i Σ x 2 , i 2 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ a 0 a 1 a 2 ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ Σ y i Σ x 1 , i y i Σ x 2 , i y i ⎦ ⎥ ⎤
( m + 1 ) × ( m + 1 ) (m+1) \times (m+1) ( m + 1 ) × ( m + 1 )
이를 Gauss Elmination 으로 구한다.
*일반적인 비선형 멱 방정식y = a 0 x 1 a 1 x 2 a 2 . . . x m a m y = a_0x_1^{a_1}x_2^{a_2} ... \ x_m^{a_m} y = a 0 x 1 a 1 x 2 a 2 . . . x m a m log y = log a 0 + a 1 log x 1 + . . . + a m log x m \log y = \log a_0+ a_1\log x_1 + ... + a_m\log x_m log y = log a 0 + a 1 log x 1 + . . . + a m log x m
Y = log y Y = \log y Y = log y A 0 = log a 0 A_0 = \log a_0 A 0 = log a 0 A 1 = a 1 , X 1 = log x 1 A_1 = a_1,\ X_1 = \log x_1 A 1 = a 1 , X 1 = log x 1 A m = a m , X m = log x m A_m = a_m, \ X_m = \log x_m A m = a m , X m = log x m
으로 치환하여 다중회귀분석을 적용할 수 있다.
s e = S S E n − ( m + 1 ) s_e = \sqrt{SS_E\over n-(m+1)} s e = n − ( m + 1 ) S S E
15-3 일반적 함수를 이용한 선형최소제곱(Linear Least-Sqaures using General Functions)
특정 함수 자체를 선형결합하여 회귀 분석을 진행할 때 사용한다.ex. sin(x), exp(x), ...
적합식 g ( x ) = a 1 f 1 ( x ) + a 2 f 2 ( x ) + . . . + a m f m ( x ) = Σ j m a j f j ( x ) g(x) = a_1f_1(x) + a_2f_2(x) + ... + a_mf_m(x) = \Sigma^m_ja_jf_j(x) g ( x ) = a 1 f 1 ( x ) + a 2 f 2 ( x ) + . . . + a m f m ( x ) = Σ j m a j f j ( x ) r i = y i − Σ j m a j f j ( x ) r_i = y_i - \Sigma^m_ja_jf_j(x) r i = y i − Σ j m a j f j ( x ) S r = Σ i n ( r i ) 2 S_r = \Sigma^n_i(r_i)^2 S r = Σ i n ( r i ) 2
S r S_r S r a 1 a_1 a 1 a m a_m a m ∂ S r ∂ a k = 0 {\partial S_r \over \partial a_k}= 0 ∂ a k ∂ S r = 0 Σ j = 1 m ( Σ i = 1 n f j ( x i ) f k ( x i ) ) a j \Sigma^m_{j=1}(\Sigma^n_{i=1}f_j(x_i)f_k(x_i))a_j Σ j = 1 m ( Σ i = 1 n f j ( x i ) f k ( x i ) ) a j = Σ y i f k ( x i ) = \Sigma y_if_k(x_i) = Σ y i f k ( x i )
[ Σ f 1 f 1 Σ f 2 f 1 Σ f 3 f 1 . . . Σ f m f 1 Σ f 1 f 2 Σ f 2 f 2 Σ f 3 f 2 . . . Σ f m f 2 . . . Σ f m f 1 Σ f m f 2 Σ f m f 3 . . . Σ f m f m ] \begin{bmatrix} \Sigma f_1f_1 & \Sigma f_2f_1 & \Sigma f_3f_1 & ... &\Sigma f_mf_1 \ \\ \Sigma f_1f_2 & \Sigma f_2f_2 & \Sigma f_3f_2 & ... &\Sigma f_mf_2 \\ & & . \\ & & . \\ & & . \\ \Sigma f_mf_1 & \Sigma f_mf_2 & \Sigma f_mf_3 & ... & \Sigma f_mf_m \\ \end{bmatrix} ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ Σ f 1 f 1 Σ f 1 f 2 Σ f m f 1 Σ f 2 f 1 Σ f 2 f 2 Σ f m f 2 Σ f 3 f 1 Σ f 3 f 2 . . . Σ f m f 3 . . . . . . . . . Σ f m f 1 Σ f m f 2 Σ f m f m ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ [ a 0 a 1 . . . a m ] \begin{bmatrix} a_0 \\ a_1\\ . \\ . \\ . \\ a_m \\ \end{bmatrix} ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ a 0 a 1 . . . a m ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ [ Σ y i f 1 Σ y i f 2 . . . Σ y i f m ] \begin{bmatrix} \Sigma y_if_1 \\ \Sigma y_if_2\\ . \\ . \\ . \\ \Sigma y_if_m \\ \end{bmatrix} ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ Σ y i f 1 Σ y i f 2 . . . Σ y i f m ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
m × m m \times m m × m
s e = S S E n − ( m + 1 ) s_e = \sqrt{SS_E\over n-(m+1)} s e = n − ( m + 1 ) S S E
15-4 비선형 회귀분석 (Nonlinear Regression)
매개변수 a 0 , a 1 , . . . a_0, a_1, ... a 0 , a 1 , . . .
g ( x ) = a 0 ( 1 − e − a 1 x ) g(x) = a_0(1- e^{-a_1x}) g ( x ) = a 0 ( 1 − e − a 1 x ) S r = Σ i = 1 n ( y i − a 0 ( 1 − e − a 1 x ) ) 2 S_r = \Sigma^n_{i=1}(y_i - a_0(1- e^{-a_1x}))^2 S r = Σ i = 1 n ( y i − a 0 ( 1 − e − a 1 x ) ) 2
CHAPTER 16 푸리에 분석(Fourier Analysis)
16-1 사인함수를 이용한 곡선 집합
1) 주기함수(Periodic Functions)
f ( t ) = f ( t + T ) f(t) = f(t+T) f ( t ) = f ( t + T )
대표적인 주기 함수
일반표현식
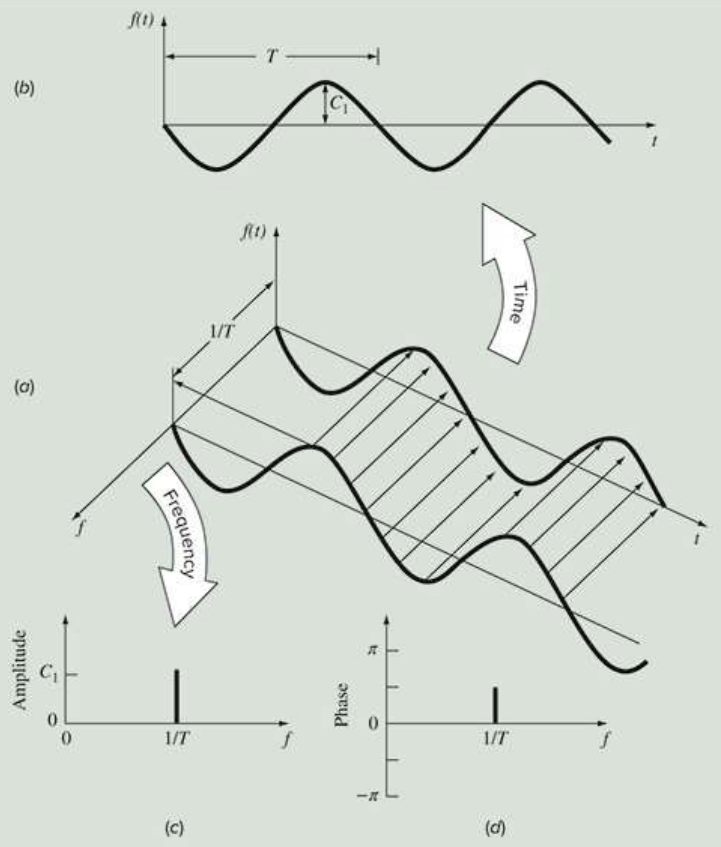
f ( t ) = A 0 + C 1 cos ( ω 0 t + θ ) f(t) = A_0 + C_1 \cos(\omega_0t + \theta) f ( t ) = A 0 + C 1 cos ( ω 0 t + θ )
A 0 A_0 A 0 C 1 C_1 C 1 ω 0 t \omega_0t ω 0 t θ \theta θ f ( 0 ) f(0) f ( 0 )
ω 0 = 2 π f \omega_0 = 2\pi f ω 0 = 2 π f f = 1 T f = {1 \over T} f = T 1
f f f T T T
cos ( A + B ) = cos A cos B − sin A sin B \cos(A+B) = \cos A \cos B - \sin A \sin B cos ( A + B ) = cos A cos B − sin A sin B cos ( ω 0 t + θ ) = cos ( w 0 t ) cos θ − sin ( w 0 t ) sin θ \cos(\omega_0t + \theta) = \cos(w_0t)\cos\theta - \sin(w_0t)\sin\theta cos ( ω 0 t + θ ) = cos ( w 0 t ) cos θ − sin ( w 0 t ) sin θ
f ( t ) = A 0 + A 1 cos ( w 0 t ) + B 1 sin ( w 0 t ) f(t) = A_0 + A_1\cos(w_0t)+B_1\sin(w_0t) f ( t ) = A 0 + A 1 cos ( w 0 t ) + B 1 sin ( w 0 t )
A 1 = C 1 cos θ A_1 = C_1\cos\theta A 1 = C 1 cos θ B 1 = − C 1 sin θ B_1 = - C_1\sin\theta B 1 = − C 1 sin θ θ = t a n − 1 ( − B 1 A 1 ) \theta = tan^{-1}(- {B_1\over A_1}) θ = t a n − 1 ( − A 1 B 1 ) C 1 = A 1 2 + B 1 2 C_1 = \sqrt {A_1^2 + B_1^2} C 1 = A 1 2 + B 1 2
이렇게 구한 f(t)를 '일반적 함수를 이용한 선형최소제곱'에서 각각 1, cos ( w 0 t ) \cos(w_0t) cos ( w 0 t ) sin ( w 0 t ) \sin(w_0t) sin ( w 0 t ) A 0 , A 1 , B 1 A_0, A_1, B_1 A 0 , A 1 , B 1
2) 사인곡선의 최소제곱 접합
f ( t ) = A 0 + A 1 cos ( ω 0 t ) + B 1 sin ( ω 0 t ) + e = g + e f(t) = A_0 + A_1\cos(\omega_0t)+B_1\sin(\omega_0t) + e = g + e f ( t ) = A 0 + A 1 cos ( ω 0 t ) + B 1 sin ( ω 0 t ) + e = g + e
r i = y i − g r_i = y_i - g r i = y i − g S r = Σ i n ( r i 2 ) = Σ i n ( y i − A 0 − A 1 cos ( ω 0 t ) − B 1 sin ( ω 0 t ) ) 2 S_r = \Sigma^n_i(r_i^2) = \Sigma^n_i(y_i - A_0 - A_1\cos(\omega_0t)-B_1\sin(\omega_0t))^2 S r = Σ i n ( r i 2 ) = Σ i n ( y i − A 0 − A 1 cos ( ω 0 t ) − B 1 sin ( ω 0 t ) ) 2 S r S_r S r A 0 , A 1 , B 1 A_0, A_1, B_1 A 0 , A 1 , B 1 ∂ S r ∂ A 0 \partial S_r \over\partial A_0 ∂ A 0 ∂ S r ∂ S r ∂ A 1 \partial S_r \over \partial A_1 ∂ A 1 ∂ S r ∂ S r ∂ B 1 \partial S_r \over\partial B_1 ∂ B 1 ∂ S r
[ n Σ cos ( ω 0 t ) Σ sin ( ω 0 t ) Σ cos ( ω 0 t ) Σ cos 2 ( ω 0 t ) Σ cos ( ω 0 t ) sin ( ω 0 t ) Σ sin ( ω 0 t ) Σ cos ( ω 0 t ) sin ( ω 0 t ) Σ sin 2 ( ω 0 t ) ] \begin{bmatrix} n & \Sigma\cos(\omega_0t) & \Sigma\sin(\omega_0t) \\ \Sigma\cos(\omega_0t) & \Sigma \cos^2(\omega_0t) & \Sigma \cos(\omega_0t)\sin(\omega_0t) \\ \Sigma\sin(\omega_0t) & \Sigma\cos(\omega_0t)\sin(\omega_0t) & \Sigma\sin^2(\omega_0t) \\ \end{bmatrix} ⎣ ⎢ ⎡ n Σ cos ( ω 0 t ) Σ sin ( ω 0 t ) Σ cos ( ω 0 t ) Σ cos 2 ( ω 0 t ) Σ cos ( ω 0 t ) sin ( ω 0 t ) Σ sin ( ω 0 t ) Σ cos ( ω 0 t ) sin ( ω 0 t ) Σ sin 2 ( ω 0 t ) ⎦ ⎥ ⎤ [ A 0 A 1 B 1 ] \begin{bmatrix} A_0 \\ A_1\\ B_1 \\ \end{bmatrix} ⎣ ⎢ ⎡ A 0 A 1 B 1 ⎦ ⎥ ⎤ [ Σ y Σ y cos ( ω 0 t ) Σ y sin ( ω 0 t ) ] \begin{bmatrix} \Sigma y\\ \Sigma y \cos(\omega_0t)\\ \Sigma y \sin(\omega_0t) \\ \end{bmatrix} ⎣ ⎢ ⎡ Σ y Σ y cos ( ω 0 t ) Σ y sin ( ω 0 t ) ⎦ ⎥ ⎤
이는 sin, cos의 주기함수가 주기 만큼의 합을 구하면 0인 것과 배각 공식을 활용하면 다음과 같이 정리할 수 있다.
[ n 0 0 0 n 2 0 0 0 n 2 ] \begin{bmatrix} n & 0 & 0 \\ 0 & {n \over 2} & 0 \\ 0 & 0 & {n \over 2} \\ \end{bmatrix} ⎣ ⎢ ⎡ n 0 0 0 2 n 0 0 0 2 n ⎦ ⎥ ⎤ [ A 0 A 1 B 1 ] \begin{bmatrix} A_0 \\ A_1\\ B_1 \\ \end{bmatrix} ⎣ ⎢ ⎡ A 0 A 1 B 1 ⎦ ⎥ ⎤ [ Σ y Σ y cos ( ω 0 t ) Σ y sin ( ω 0 t ) ] \begin{bmatrix} \Sigma y\\ \Sigma y \cos(\omega_0t)\\ \Sigma y \sin(\omega_0t) \\ \end{bmatrix} ⎣ ⎢ ⎡ Σ y Σ y cos ( ω 0 t ) Σ y sin ( ω 0 t ) ⎦ ⎥ ⎤
A 0 = Σ y n , A 1 = 2 n Σ y cos ( ω 0 t ) , B 1 = 2 n Σ y sin ( ω 0 t ) A_0 = {\Sigma y\over n}, A_1 = {2 \over n}\Sigma y\cos(\omega_0t), B_1 = {2 \over n}\Sigma y\sin(\omega_0t) A 0 = n Σ y , A 1 = n 2 Σ y cos ( ω 0 t ) , B 1 = n 2 Σ y sin ( ω 0 t )
*배각공식
cos 2 θ = 2 cos 2 θ − 1 = 1 − 2 sin 2 θ \cos2\theta = 2\cos^2\theta-1 = 1-2\sin^2\theta cos 2 θ = 2 cos 2 θ − 1 = 1 − 2 sin 2 θ sin 2 θ = 2 sin θ c o s θ \sin2\theta = 2\sin\theta cos\theta sin 2 θ = 2 sin θ c o s θ
3) 사인곡선의 최소제곱 접합 일반적 모델 확장
f ( t ) = A 0 + A 1 cos ( ω 0 t ) + B 1 sin ( ω 0 t ) + A 2 cos ( 2 ω 0 t ) + B 2 sin ( 2 ω 0 t ) + . . . + A m cos ( m ω 0 t ) + B m sin ( m ω 0 t ) f(t) = A_0 + A_1\cos(\omega_0t)+B_1\sin(\omega_0t) + A_2\cos(2\omega_0t)+B_2\sin(2\omega_0t) + ... + A_m\cos(m\omega_0t)+B_m\sin(m\omega_0t) f ( t ) = A 0 + A 1 cos ( ω 0 t ) + B 1 sin ( ω 0 t ) + A 2 cos ( 2 ω 0 t ) + B 2 sin ( 2 ω 0 t ) + . . . + A m cos ( m ω 0 t ) + B m sin ( m ω 0 t )
n개의 등간격 데이터에 대해 접합
A 0 = Σ y n A_0 = {\Sigma y \over n} A 0 = n Σ y
A j = 2 n Σ y cos ( j ω 0 t ) A_j = {2 \over n}\Sigma y\cos(j\omega_0t) A j = n 2 Σ y cos ( j ω 0 t ) B j = 2 n Σ y sin ( j ω 0 t ) B_j = {2 \over n}\Sigma y\sin(j\omega_0t) B j = n 2 Σ y sin ( j ω 0 t )
총 미지수의 갯수 = 2m+1
n > 2m+1: 회귀분석
n = 2m+1: 보간법.
16-2 연속 Fourier 급수 (Continuous Fourier Series)
임의의 주기함수를 조화 관계의 주파수를 가지는 사인 곡선들의 무한급수로 나타낼 수 있고, 이 급수를 Fourier 급수라고 한다.
f ( t ) = a 0 + a 1 cos ( ω 0 t ) + b 1 sin ( ω 0 t ) + a 2 cos ( 2 ω 0 t ) + b 2 sin ( 2 ω 0 t ) + . . . f(t) = a_0 + a_1\cos(\omega_0t)+b_1\sin(\omega_0t) + a_2\cos(2\omega_0t)+b_2\sin(2\omega_0t) + ... f ( t ) = a 0 + a 1 cos ( ω 0 t ) + b 1 sin ( ω 0 t ) + a 2 cos ( 2 ω 0 t ) + b 2 sin ( 2 ω 0 t ) + . . . a 0 + Σ k = 1 ∞ ( a k cos ( k ω 0 t ) + b k sin ( k ω t ) ) a_0 + \Sigma^{\infin}_{k=1}(a_k\cos(k\omega_0t) + b_k\sin(k\omega t)) a 0 + Σ k = 1 ∞ ( a k cos ( k ω 0 t ) + b k sin ( k ω t ) )
a 0 = 1 T ∫ 0 T f ( t ) d t a_0 = {1 \over T} \int^T_0f(t)dt a 0 = T 1 ∫ 0 T f ( t ) d t a k = 2 T ∫ 0 T f ( t ) cos ( k ω 0 t ) d t a_k = {2 \over T} \int^T_0f(t)\cos(k\omega_0t) dt a k = T 2 ∫ 0 T f ( t ) cos ( k ω 0 t ) d t b k = 2 T ∫ 0 T f ( t ) sin ( k ω 0 t ) d t b_k = {2 \over T} \int^T_0f(t)\sin(k\omega_0t) dt b k = T 2 ∫ 0 T f ( t ) sin ( k ω 0 t ) d t
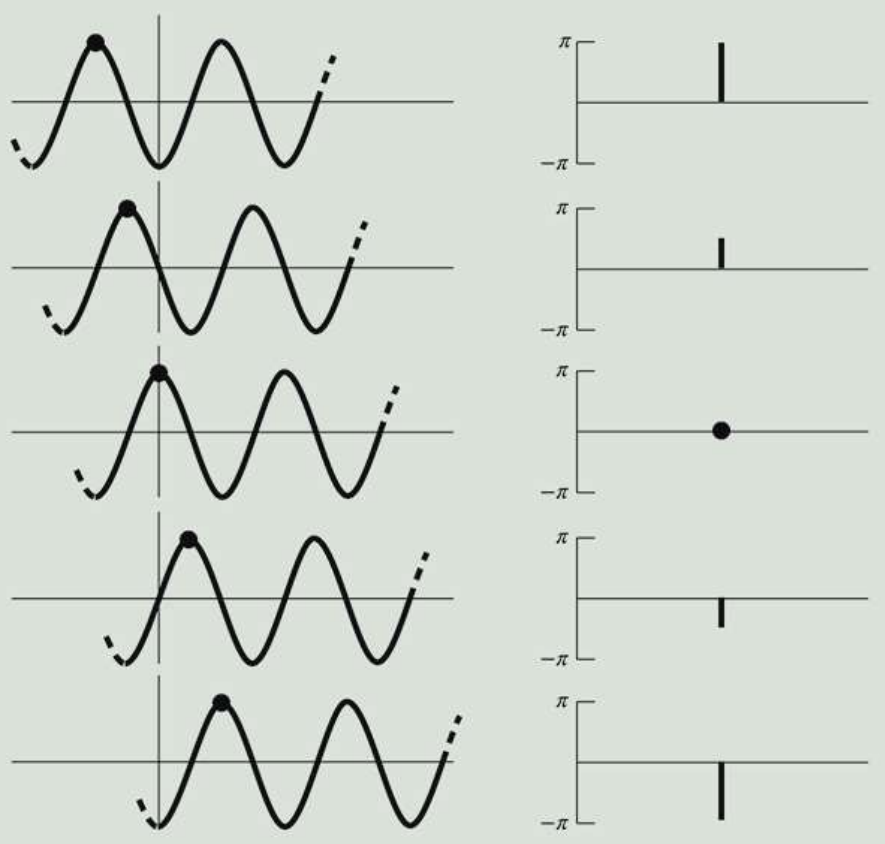
16-3 주파수 영역과 시간 영역(Time versus Frequency Domains)
sin 함수를 시간축이 아닌 주파수축으로 표현할 수 있다.
진폭-주파수 그래프, 위상각-주파수 그래프
1) 위상각의 부호(Sign of Phase)
위상각: 0에서 양의 최대값이 발생하는 지점까지의 거리 (radian)
+: 원점 이전에 최대값 발생
-: 원점 이후에 최대값 발생
16-4 Fourier 변환, 이산 Fourier 변환 (DFT)
1) Fourier 적분과 변환
Fourier 적분: 비주기적 파형을 삼각함수의 급수 나타내는 방법
비주기성으로 만들기 위해 T → ∞ \infin ∞
Fourier 변환쌍 (시간영역 ↔ 주파수영역)
시간영역: F ( ω ) F(\omega) F ( ω ) f ( t ) = 1 2 π ∫ − ∞ ∞ F ( ω ) e i ω t d w f(t) = {1 \over 2\pi}\int^\infin_{-\infin}F(\omega)e^{i\omega t}dw f ( t ) = 2 π 1 ∫ − ∞ ∞ F ( ω ) e i ω t d w
주파수 영역: f ( t ) f(t) f ( t ) F ( ω ) = ∫ − ∞ ∞ f ( t ) e − i ω t d t F(\omega) = \int^\infin_{-\infin} f(t)e^{-i\omega t}dt F ( ω ) = ∫ − ∞ ∞ f ( t ) e − i ω t d t
2) 이산 Fourier 변환 (DFT)
이산 형태로 수집된 데이터에 대한 Fourier 변환
*이산 데이터: 불연속 데이터
0~T 구간을 n개의 등간격으로 나눈다.Δ t = T n \Delta t = {T \over n} Δ t = n T ( t 0 , f 0 ) , ( t 1 , f 1 ) , . . . ( t n − 1 , f n − 1 ) (t_0, f_0),\ (t_1, f_1),\ ...\ (t_{n-1},\ f_{n-1}) ( t 0 , f 0 ) , ( t 1 , f 1 ) , . . . ( t n − 1 , f n − 1 )
이산 Fourier 변환F k = Σ j = 0 n − 1 f j e − i k ω 0 j F_k = \Sigma^{n-1}_{j=0} f_je^{-ik\omega_0j} F k = Σ j = 0 n − 1 f j e − i k ω 0 j
역 Fourier 변환f j = 1 n Σ k = 0 n − 1 F k e i k w o j f_j = {1\over n}\Sigma^{n-1}_{k=0} F_ke^{ikw_oj} f j = n 1 Σ k = 0 n − 1 F k e i k w o j
n = 2 π n n = {2\pi \over n} n = n 2 π
기존 적분에서 sigma 로 변환된 형태.
측정할 수 있는 가장 높은 주파수
f m a x = 1 2 × 샘플링 주파수 f_{max} = {1\over 2} \times \text{샘플링 주파수} f m a x = 2 1 × 샘플링 주파수
나이퀴스트 주파수(Nyquist Frequency) 라고 부른다.
샘플링 간격: 주기 함수에서 한 사이클 내 최대 최소 사이의 간격π 2 \pi \over 2 2 π 3 π 2 3\pi \over 2 2 3 π π \pi π
측정할 수 있는 가장 낮은 주파수
f m i n = 1 샘플길이시간 f_{min} = {1 \over \text{샘플길이시간}} f m i n = 샘플길이시간 1
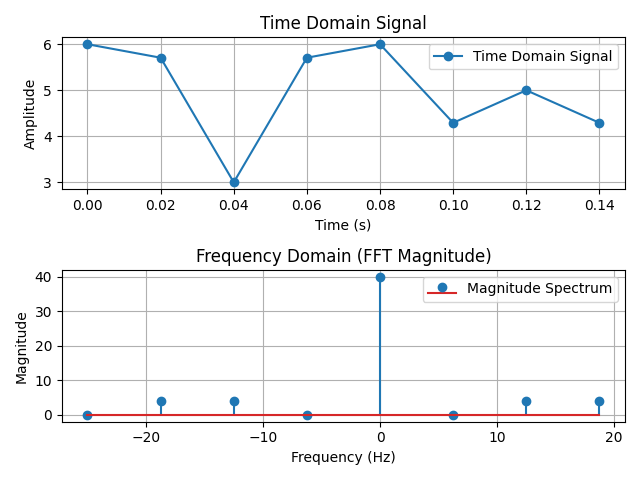
16-5 고속 Fourier 변환 (FFT)
삼각함수의 주기성과 대칭성을 이용해 DFT를 효과적으로 계산하는 알고리즘.O ( n ) = n log n O(n) = n\log n O ( n ) = n log n
1) cooley tukey 알고리즘
F k = Σ j = 0 n − 1 f j e − i k ω 0 j = Σ j = 0 n 2 − 1 f 2 j e − i k j 4 π n + e − i k 2 π n Σ j = 0 n 2 − 1 f 2 j + 1 e − i k j 4 π n F_k = \Sigma^{n-1}_{j=0} f_je^{-ik\omega_0j} = \Sigma^{{n \over 2}-1}_{j=0}f_{2j}e^{-ikj 4\pi \over n} + e^{-ik2\pi \over n} \Sigma^{{n \over 2}-1}_{j=0}f_{2j+1}e^{-ikj 4\pi \over n} F k = Σ j = 0 n − 1 f j e − i k ω 0 j = Σ j = 0 2 n − 1 f 2 j e n − i k j 4 π + e n − i k 2 π Σ j = 0 2 n − 1 f 2 j + 1 e n − i k j 4 π
F k + n 2 = Σ j = 0 n 2 − 1 f 2 j e − i k j 4 π n − e − i k 2 π n Σ j = 0 n 2 − 1 f 2 j + 1 e − i k j 4 π n F_{k + {n \over 2}} = \Sigma^{{n \over 2}-1}_{j=0}f_{2j}e^{-ikj 4\pi \over n} - e^{-ik2\pi \over n} \Sigma^{{n \over 2}-1}_{j=0}f_{2j+1}e^{-ikj 4\pi \over n} F k + 2 n = Σ j = 0 2 n − 1 f 2 j e n − i k j 4 π − e n − i k 2 π Σ j = 0 2 n − 1 f 2 j + 1 e n − i k j 4 π
즉, F k F_k F k F k + n 2 F_{k + {n \over 2}} F k + 2 n
2) FFT 코드
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
n = 8
dt = 0.02
fs = 1/dt
T = 0.16
tspan = np.arange(0, n) * dt # 시간 축 배열 (0부터 (n-1)*dt까지의 시간 값)
freq = fftfreq(n, d=dt) # FFT 결과에 대응하는 주파수 축
y = 5 + np.cos(2*np.pi*12.5*tspan) + np.sin(2*np.pi*18.75*tspan) # 시간영역의 주기함수
Y = fft(y) # 주파수영역으로 변환
magnitude = np.abs(Y)
phase = np.angle(Y)
nyquist = fs/2 # 최대 주파수 (나이퀴스트 주파수)
# 1. 시간 영역 신호
plt.subplot(2, 1, 1)
plt.plot(tspan, y, marker='o', label="Time Domain Signal")
plt.title("Time Domain Signal")
plt.xlabel("Time (s)")
plt.ylabel("Amplitude")
plt.grid()
plt.legend()
# 2. 주파수 영역 신호 (크기 스펙트럼)
plt.subplot(2, 1, 2)
plt.stem(freq, magnitude, use_line_collection=True, label="Magnitude Spectrum")
plt.title("Frequency Domain (FFT Magnitude)")
plt.xlabel("Frequency (Hz)")
plt.ylabel("Magnitude")
plt.grid()
plt.legend()
plt.tight_layout() # 요소 간 간격 자동 조정
plt.show()CHAPTER 17 다항식보간법(Polynomial Interpolation)
17-1 보간법 개요 및 Newton 보간다항식
1) 다항식 보간법 개요
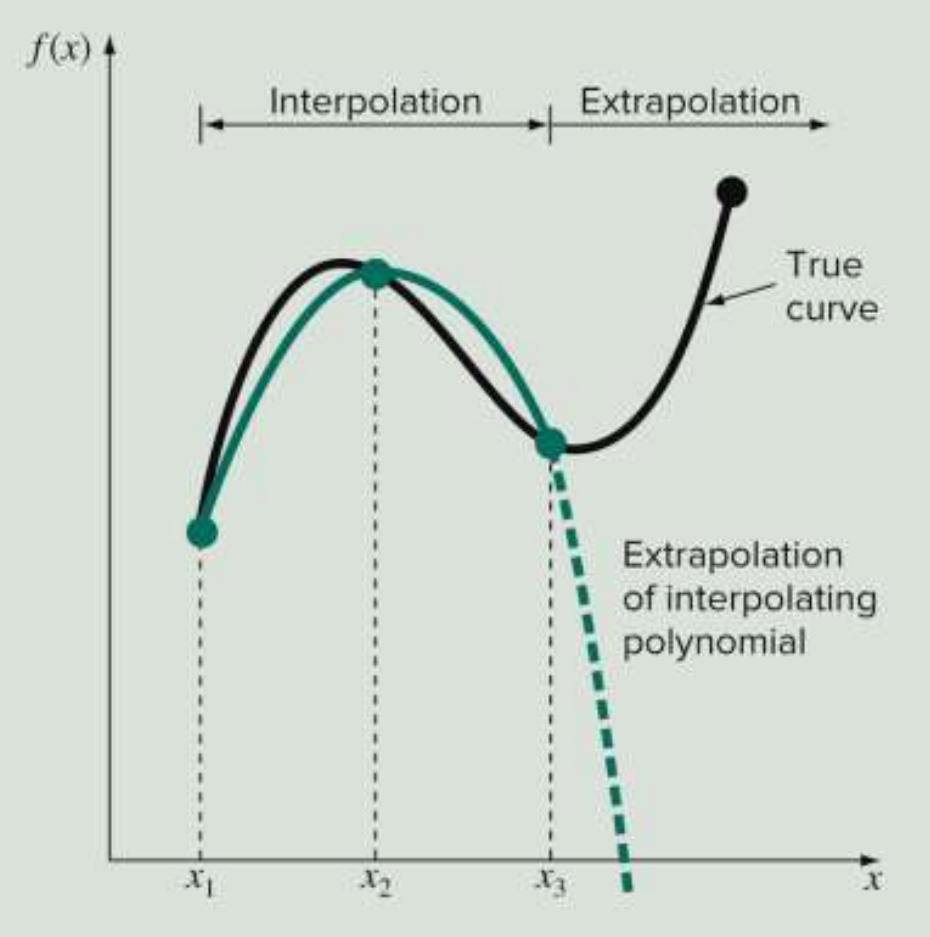
보간법(Interpolation): 정확한 데이터 점들 사이에 있는 중간값을 추정하는 기법.
*외삽법(Extrapolation): 주어진 데이터 점들 밖에 있는 값 추정
다항식 보간법: n개 점 데이터를 보간하기 위해 (n-1)차 다항식 사용g ( x ) = a 1 + a 2 x + a 3 x 2 + . . . + a n x n − 1 g(x) = a_1 + a_2x + a_3x^2 + ... + a_nx^{n-1} g ( x ) = a 1 + a 2 x + a 3 x 2 + . . . + a n x n − 1 유일한 다항식.→ 다양한 보간법을 사용해도 결국에 나오는 다항식은 동일함.
세 개의 점 데이터 (x1, g1), (x2, g2), (x3, g3)g ( x ) = P 1 x 2 + P 2 x + P 3 g(x) = P_1x^2 + P_2x + P_3 g ( x ) = P 1 x 2 + P 2 x + P 3
g 1 = P 1 x 1 2 + P 2 x 1 + P 3 g_1 = P_1x_1^2 + P_2x_1 + P_3 g 1 = P 1 x 1 2 + P 2 x 1 + P 3 g 2 = P 1 x 2 2 + P 2 x 2 + P 3 g_2 = P_1x_2^2 + P_2x_2 + P_3 g 2 = P 1 x 2 2 + P 2 x 2 + P 3 g 3 = P 1 x 3 2 + P 2 x 3 + P 3 g_3 = P_1x_3^2 + P_2x_3 + P_3 g 3 = P 1 x 3 2 + P 2 x 3 + P 3
[ x 1 2 x 1 1 x 2 2 x 2 1 x 3 2 x 3 1 ] \begin{bmatrix} x_1^2 & x_1 & 1 \\ x_2^2 & x_2 & 1 \\ x_3^2 & x_3 & 1 \\ \end{bmatrix} ⎣ ⎢ ⎡ x 1 2 x 2 2 x 3 2 x 1 x 2 x 3 1 1 1 ⎦ ⎥ ⎤ [ P 1 P 2 P 3 ] \begin{bmatrix} P_1 \\ P_2 \\ P_3 \\ \end{bmatrix} ⎣ ⎢ ⎡ P 1 P 2 P 3 ⎦ ⎥ ⎤ [ g 1 g 2 g 3 ] \begin{bmatrix} g_1 \\ g_2\\ g_3\\ \end{bmatrix} ⎣ ⎢ ⎡ g 1 g 2 g 3 ⎦ ⎥ ⎤
P = A − 1 g P = A^{-1}g P = A − 1 g
이 때의 A 행렬을 Vandermonde 행렬이라고 하고, 이 과정을 Gauss-Elimination 등을 통해 구할 수 있다. 하지만, 이 방식은 Vandermonde 행렬이 불량조건이 매우 큰 행렬이라 반올림 오차에 민감하게 되고, 더 정확한 값을 구하기 위해 다른 보간법을 사용한다.
(한꺼번에 구하는 방식)
import numpy as np
def runge(x):
return 1 / (1 + 25*x**2)
x = np.array([-5, 0, 5])
G = np.reshape(runge(x), (len(x), 1))
A = np.array([[j**i for i in range(len(x)-1, -1, -1)] for j in x])
vnd = np.vander(x) # = A
print(vnd)
P = np.linalg.solve(A, G)
print(A)
print(P)
print(G)2) Newton 보간다항식
n개의 점에서 각각 점이 하나씩 들어갈 때마다 각각의 계수를 결정하는 방식.
선형보간법
직선으로 보간하는 방법
2개의 점 요구 (x1, f1), (x2, f2)
g(x) 결정 방식
첫번째 점을 대입 했을 때 b1 결정
두번째 점을 대입 했을 때 b2 결정
g(x) = b1+ b2(x - x1)
f1 = b1
b 2 = f 2 − f 1 x 2 − x 1 b_2 = {f_2-f_1 \over x_2-x_1} b 2 = x 2 − x 1 f 2 − f 1
→ g ( x ) = f 1 + f 2 − f 1 x 2 − x 1 ( x − x 1 ) g(x) = f_1 + {f_2-f_1 \over x_2-x_1} (x-x_1) g ( x ) = f 1 + x 2 − x 1 f 2 − f 1 ( x − x 1 )
2차 보간법
2차항을 사용해 보간하는 방법
3개의 점 요구 (x1, f1), (x2, f2), (x3, f3)
g(x) 결정 방식
첫번째 점을 대입 했을 때 b1 결정
두번째 점을 대입 했을 때 b2 결정
세번째 점을 대입 했을 때 b3 결정
g(x) = b1 + b2(x-x1) + b3(x-x1)(x-x2)
f1 = b1b 2 = f 2 − f 1 x 2 − x 1 b_2 = {f_2 - f_1 \over x_2-x_1} b 2 = x 2 − x 1 f 2 − f 1 b 3 = f 3 − f 2 x 3 − x 2 − f 2 − f 1 x 2 − x 1 x 3 − x 1 b_3 = {{f_3 - f_2 \over x_3-x_2} - {f_2 - f_1 \over x_2-x_1} \over x_3 - x_1} b 3 = x 3 − x 1 x 3 − x 2 f 3 − f 2 − x 2 − x 1 f 2 − f 1
n차 보간법
n개의 점 데이터에 n-1 차 다항식을 접합
g ( x ) = b 1 + b 2 ( x − x 1 ) + b 3 ( x − x 1 ) ( x − x 2 ) . . . + b n ( x − x 1 ) ( x − x 2 ) . . . ( x − x n − 1 ) g(x) = b_1 + b_2(x-x_1) + b_3(x-x_1)(x-x_2) ... + b_n(x-x_1)(x-x_2)...(x-x_{n-1}) g ( x ) = b 1 + b 2 ( x − x 1 ) + b 3 ( x − x 1 ) ( x − x 2 ) . . . + b n ( x − x 1 ) ( x − x 2 ) . . . ( x − x n − 1 )
b1 = f(x1)
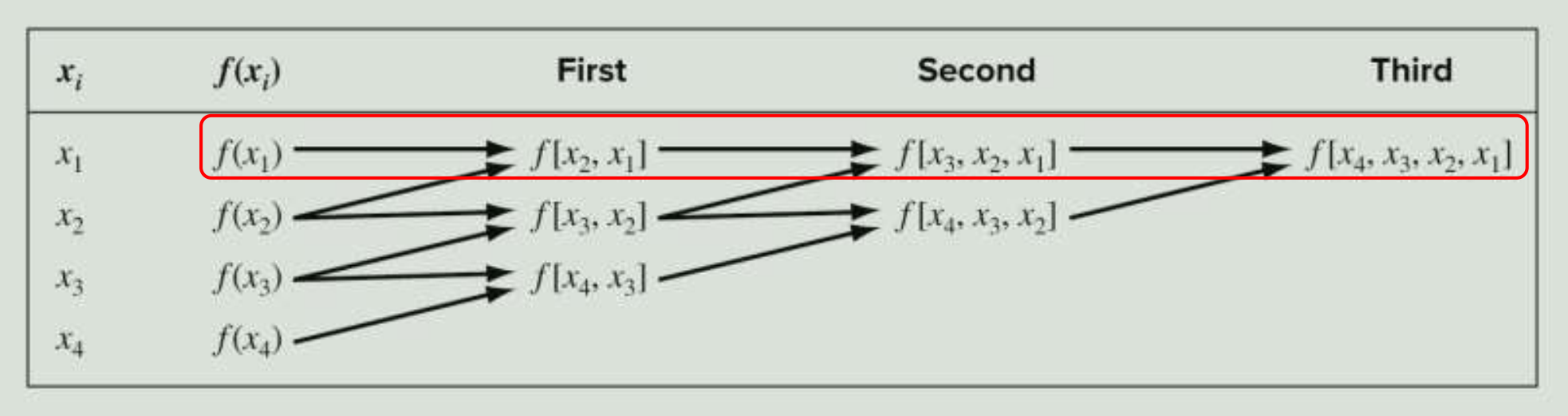
차분표 제작
g ( x ) = f ( x 1 ) + f ( x 2 , x 1 ) ( x − x 1 ) + f ( x 3 , x 2 , x 1 ) ( x − x 1 ) ( x − x 2 ) + f ( x 4 , x 3 , x 2 , x 1 ) ( x − x 1 ) ( x − x 2 ) ( x − x 3 ) g(x) = f(x_1) + f(x_2, x_1)(x-x_1) + f(x_3, x_2, x_1)(x-x_1)(x-x_2) + f(x_4, x_3, x_2, x_1)(x-x_1)(x-x_2)(x-x_3) g ( x ) = f ( x 1 ) + f ( x 2 , x 1 ) ( x − x 1 ) + f ( x 3 , x 2 , x 1 ) ( x − x 1 ) ( x − x 2 ) + f ( x 4 , x 3 , x 2 , x 1 ) ( x − x 1 ) ( x − x 2 ) ( x − x 3 )
f ( x 1 ) f(x_1) f ( x 1 ) f ( x 2 , x 1 ) f(x_2, x_1) f ( x 2 , x 1 ) f ( x 3 , x 2 , x 1 ) f(x_3, x_2, x_1) f ( x 3 , x 2 , x 1 ) f ( x 4 , x 3 , x 2 , x 1 ) f(x_4, x_3, x_2, x_1) f ( x 4 , x 3 , x 2 , x 1 )
n차 분할 차분 공식f ( x n , x n − 1 , . . . , x 1 ) = f ( x n , x n − 1 , . . . , x 2 ) − f ( x n − 1 , . . . , x 1 ) x n − x 1 f(x_n, x_{n-1}, ..., x_1) = {f(x_n, x_{n-1}, ..., x_2) - f(x_{n-1}, ..., x_1) \over x_n - x_1} f ( x n , x n − 1 , . . . , x 1 ) = x n − x 1 f ( x n , x n − 1 , . . . , x 2 ) − f ( x n − 1 , . . . , x 1 )
이 공식을 바탕으로 차분표를 만들어서 구할 수 있다.
import numpy as np
def f(x):
return 1 / (1 + 25 * x**2)
def newtInt(x, y, x_val):
n = len(x)
if n != len(y):
return 'x and y must be of same length'
b = np.zeros((n, n))
b[:, 0] = np.transpose(y) # 0번째 차분 f(x_n)
# 차분표 제작
for j in range(1, n):
for i in range(n-j):
b[i, j] = (b[i+1, j-1]-b[i, j-1]) / (x[i+j]-x[i])
xt = 1
yint = b[0, 0]
for j in range(n-1):
xt *= (x_val-x[j]) # (x - xj) 누적
yint += +b[0, j+1]*xt # bj*(x-xj) 를 구해서 g(x) 만들기.
return yint
x = np.array([-1, -0.5, 0, 0.5, 1]) # 보간할 점
y = f(x) # 런게 함수 값
print(newtInt(x, y, 0.3))17-2 Lagrange 보간다항식
1) 선형보간식
직선 보간
두 점 (x1, f1), (x2, f2)
g ( x ) = L 1 f 1 + L 2 f 2 g(x) = L_1f_1 + L_2f_2 g ( x ) = L 1 f 1 + L 2 f 2
L 1 L_1 L 1 L 1 = x − x 2 x 1 − x 2 L_1 = {x-x_2 \over x_1-x_2} L 1 = x 1 − x 2 x − x 2
L 2 L_2 L 2 L 2 = x − x 1 x 2 − x 1 L_2 = {x-x_1 \over x_2-x_1} L 2 = x 2 − x 1 x − x 1
g ( x ) = x − x 2 x 1 − x 2 f 1 + x − x 1 x 2 − x 1 f 2 g(x) = {x-x_2 \over x_1-x_2}f_1 + {x-x_1 \over x_2-x_1}f_2 g ( x ) = x 1 − x 2 x − x 2 f 1 + x 2 − x 1 x − x 1 f 2
이 g(x)를 잘 정리하면 newton 보간 다항식과 같기 때문에 보간방법과 관계없이 수학적으로 동등하다.
2) 2차 Lagrange 보간식
세 점 (x1, f1), (x2, f2), (x3, f3)
g ( x ) = L 1 f 1 + L 2 f 2 + L 3 f 3 g(x) = L_1f_1 + L_2f_2 + L_3f_3 g ( x ) = L 1 f 1 + L 2 f 2 + L 3 f 3
형태로 나와야 한다.
L 1 = ( x − x 2 ) ( x − x 3 ) ( x 1 − x 2 ) ( x 1 − x 3 ) L_1 = {(x-x_2)(x-x_3) \over (x_1-x_2)(x_1-x_3)} L 1 = ( x 1 − x 2 ) ( x 1 − x 3 ) ( x − x 2 ) ( x − x 3 )
L 2 = ( x − x 1 ) ( x − x 3 ) ( x 2 − x 1 ) ( x 2 − x 3 ) L_2 = {(x-x_1)(x-x_3) \over (x_2-x_1)(x_2-x_3)} L 2 = ( x 2 − x 1 ) ( x 2 − x 3 ) ( x − x 1 ) ( x − x 3 )
L 3 = ( x − x 1 ) ( x − x 2 ) ( x 3 − x 1 ) ( x 3 − x 2 ) L_3 = {(x-x_1)(x-x_2) \over (x_3-x_1)(x_3-x_2)} L 3 = ( x 3 − x 1 ) ( x 3 − x 2 ) ( x − x 1 ) ( x − x 2 )
따라서, g ( x ) = ( x − x 2 ) ( x − x 3 ) ( x 1 − x 2 ) ( x 1 − x 3 ) f 1 + ( x − x 1 ) ( x − x 3 ) ( x 2 − x 1 ) ( x 2 − x 3 ) f 2 + ( x − x 1 ) ( x − x 2 ) ( x 3 − x 1 ) ( x 3 − x 2 ) f 3 g(x) = {(x-x_2)(x-x_3) \over (x_1-x_2)(x_1-x_3)}f_1 + {(x-x_1)(x-x_3) \over (x_2-x_1)(x_2-x_3)}f_2 + {(x-x_1)(x-x_2) \over (x_3-x_1)(x_3-x_2)}f_3 g ( x ) = ( x 1 − x 2 ) ( x 1 − x 3 ) ( x − x 2 ) ( x − x 3 ) f 1 + ( x 2 − x 1 ) ( x 2 − x 3 ) ( x − x 1 ) ( x − x 3 ) f 2 + ( x 3 − x 1 ) ( x 3 − x 2 ) ( x − x 1 ) ( x − x 2 ) f 3
3) n-1차 Lagrange 보간다항식
g ( x ) = Σ i = 1 n L i ( x ) f i g(x) = \Sigma^n_{i=1}L_i(x)f_i g ( x ) = Σ i = 1 n L i ( x ) f i
L i ( x ) = Π j = 1 , j ≠ i n x − x j x i − x j L_i(x) = \Pi^n_{j=1, j\neq i} {x - x_j \over x_i-x_j} L i ( x ) = Π j = 1 , j = i n x i − x j x − x j ( x − x 1 ) ( x − x 2 ) . . . ( x − x i − 1 ) ( x − x i + 1 ) . . . ( x − x n ) ( x i − x 1 ) ( x i − x 2 ) . . . ( x i − x i − 1 ) ( x i − x i + 1 ) . . . ( x i − x n ) ) {(x-x_1)(x-x_2)...(x-x_{i-1})(x-x_{i+1})...(x-x_n) \over (x_i-x_1)(x_i-x_2)...(x_i-x_{i-1})(x_i-x_{i+1})...(x_i-x_n))} ( x i − x 1 ) ( x i − x 2 ) . . . ( x i − x i − 1 ) ( x i − x i + 1 ) . . . ( x i − x n ) ) ( x − x 1 ) ( x − x 2 ) . . . ( x − x i − 1 ) ( x − x i + 1 ) . . . ( x − x n )
즉,x = x i , L i = 1 x = x_i, L_i= 1 x = x i , L i = 1 x ≠ x i , L i = 0 x \neq x_i, L_i=0 x = x i , L i = 0
이는 분자에 x − x i x-x_i x − x i x i − x i x_i-x_i x i − x i
import numpy as np
def f(x):
return 1 / (1 + 25 * x**2)
def Lagrange(x, y, xval):
n = len(x)
if len(y) != n:
return 'x and y must be same length'
s = 0
for i in range(n):
product = y[i] # f(i)를 먼저 곱한 후
for j in range(n):
if i != j:
product = product * (xval - x[j]) / (x[i] - x[j]) # L을 계산해서 곱해준다.
s += product # 더해서 g(x) 만들기
return s
x = np.array([-1, -0.5, 0, 0.5, 1]) # 보간할 점
y = f(x) # 런게 함수 값
print(Lagrange(x, y, 0.3))4) 오차
e ( x ) = f ( x ) − g ( x ) e(x) = f(x) - g(x) e ( x ) = f ( x ) − g ( x )
보간역의 가장자리에서 큼.
보간범위가 커지면 진동폭이 커짐.
17-3 역보간법과 외삽법 (Inverse Interpolation and Extrapolation)
1) 역보간법 (Inverse Interpolation)
통상적으로 x는 독립변수로써 등간격으로 주어지고, f(x)는 종속변수로써 부등간격으로 주어진다.
f(x)값을 알고 이에 해당하는 x값을 역으로 알고 싶을 때 역보간법을 사용한다.
f(x)를 독립변수로, x를 종속변수로 역할 교환을 하여 구하는 방법
주어진 f(x)값을 포함하는 세개의 점 데이터로 2차 보간다항식을 구한 후 근을 구하는 형식으로 x를 구한다.
2) 외삽법과 진동(Extrapolation and Oscillations)
주어진 데이터 범위 안에 있는 값은 보간법으로 잘 예측하는 경향을 보이지만 범위 바깥의 데이터는 오차가 매우 커진다. 이러한 범위 밖에 있는 f(x) 값을 예측하는 것을 외삽법으로 부른다.
진동(Oscillations)
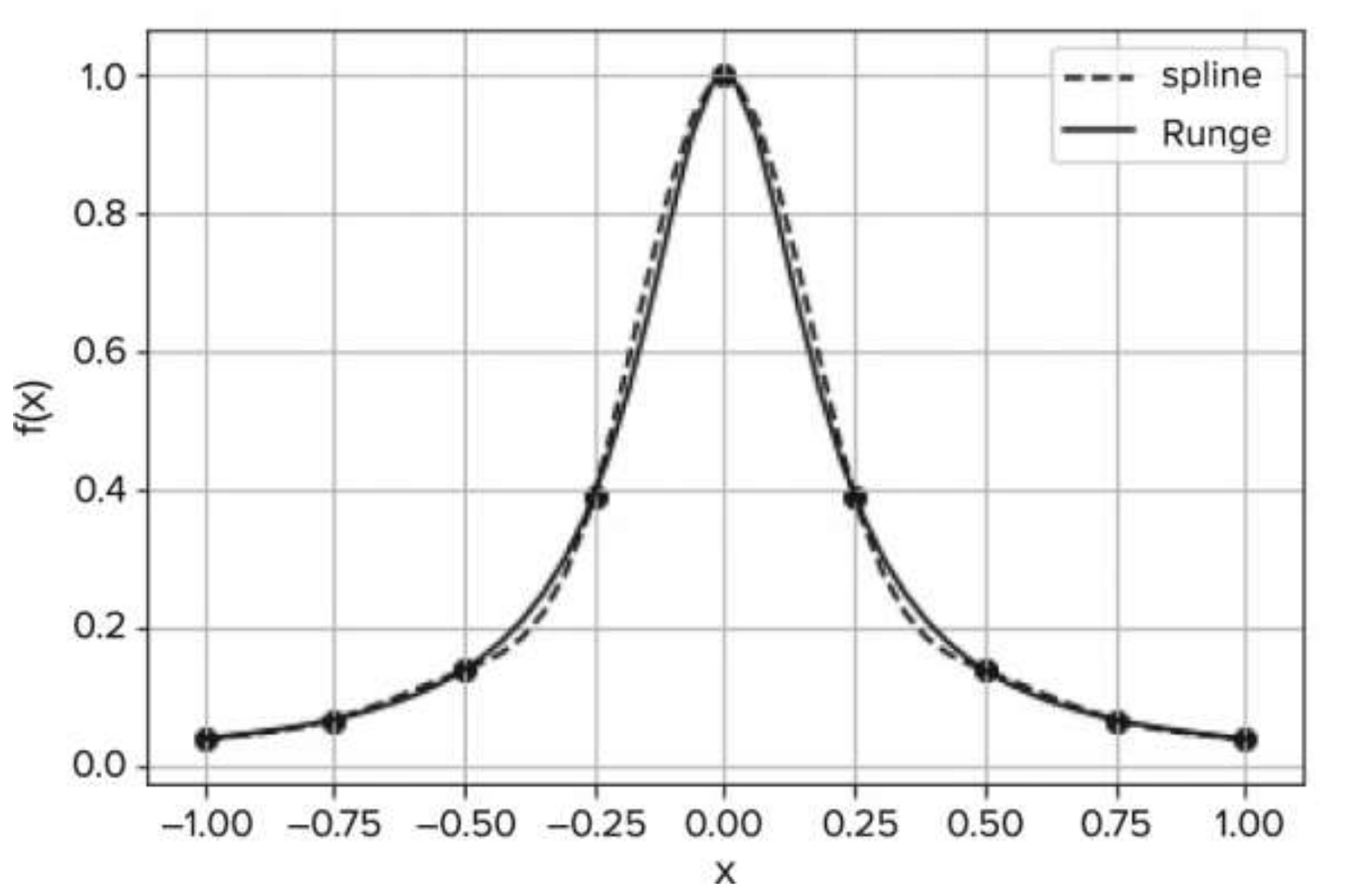
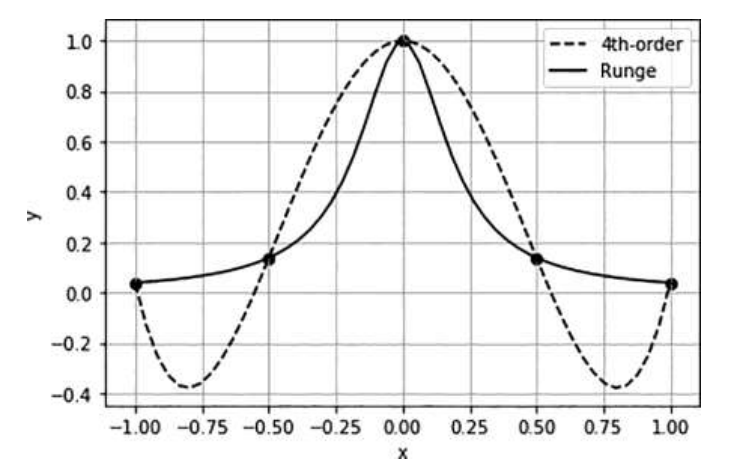
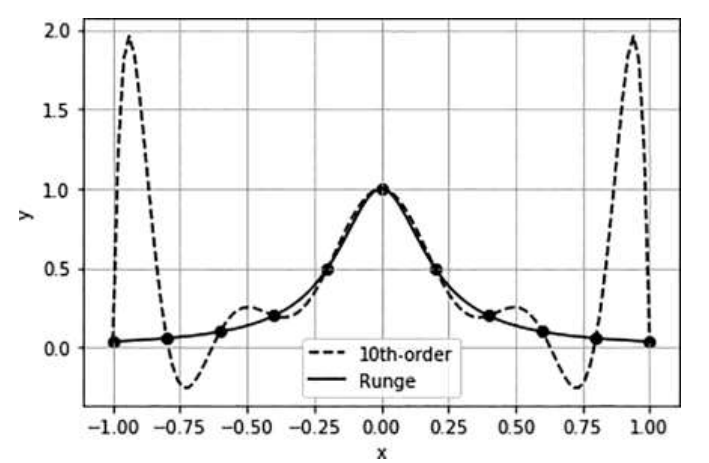
일반적으로 고차 다항식 보간법을 활용할 수록 정확도가 높아질 것으로 기대하는데, 이는 옳지 않음을 Runge 함수를 통해 증명한 결과이다.
Runge 함수: f ( x ) = 1 1 + 25 x 2 f(x) = {1 \over 1+25x^2} f ( x ) = 1 + 2 5 x 2 1
4차 다항식 보간법을 사용한 경우
10차 다항식 보간법을 사용한 경우
10차 다항식 보간법을 사용했을 때 center 부분은 더 정확도가 높으면 edge 부분으로 갈수록 오차가 매우 커짐을 알 수 있다. 이로써, 오히려 저차항 다항식 보간법이 더 잘 묘사할 때가 있음을 알아야 한다.
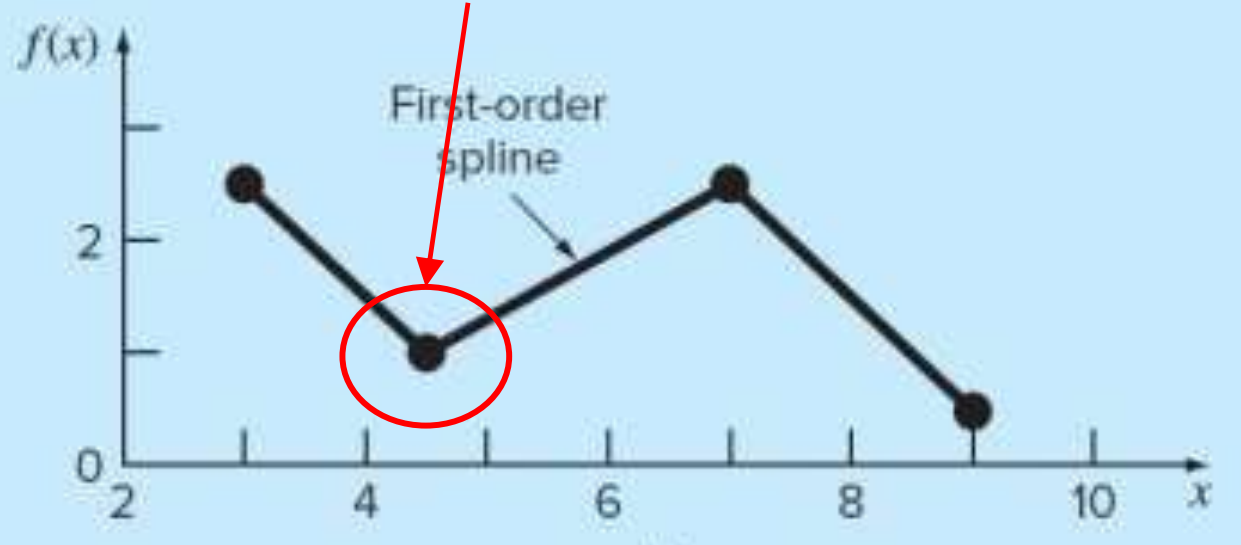
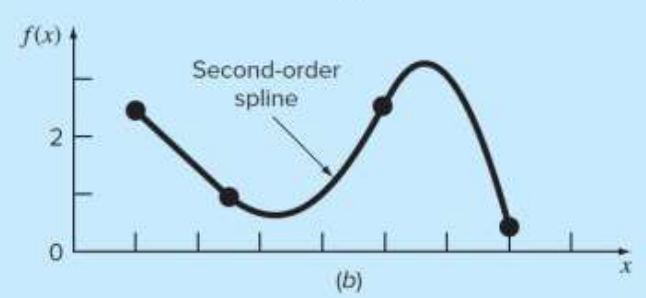
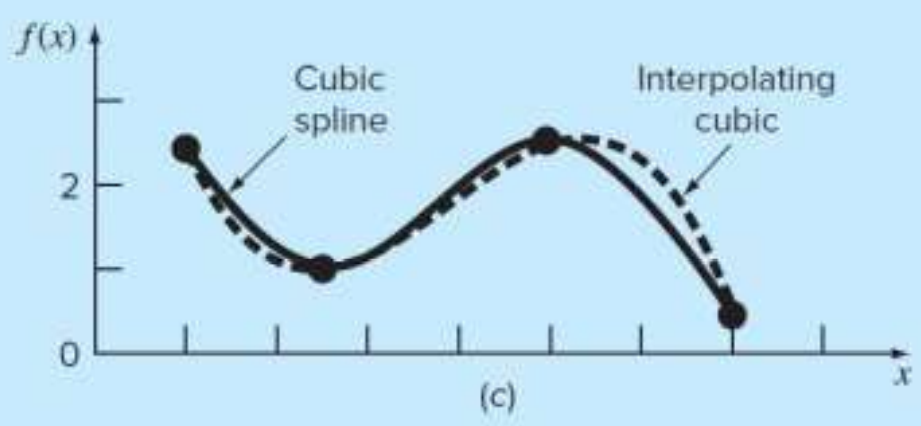
CHAPTER 18 스플라인과 소구간별 보간법
18-1 스플라인 개요 및 1차 스플라인
1) 스플라인 보간법 사용 이유
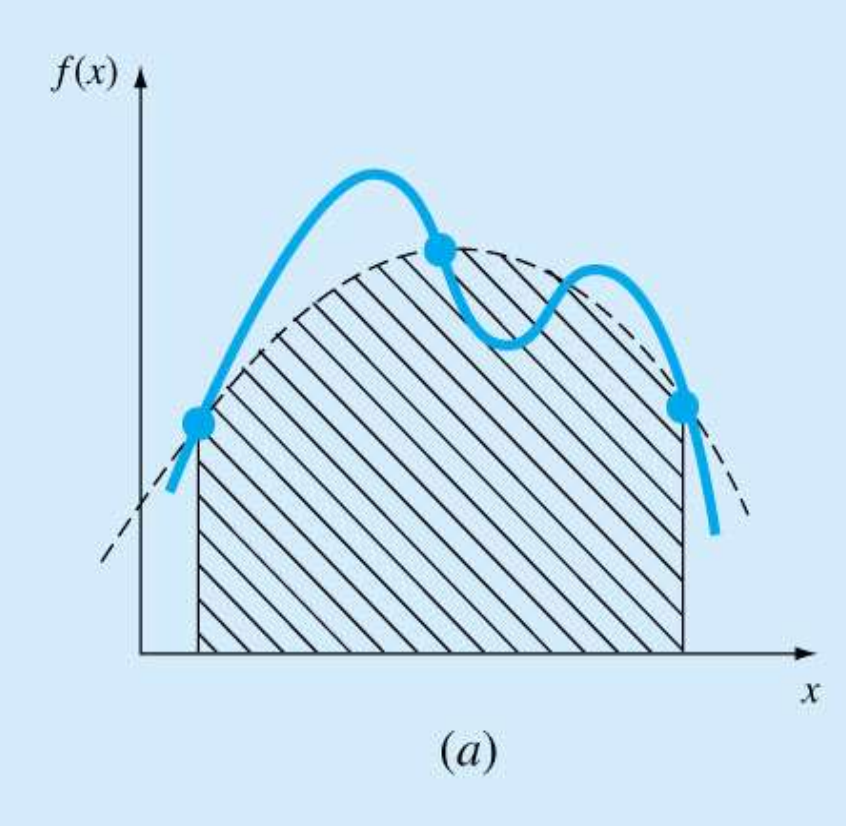
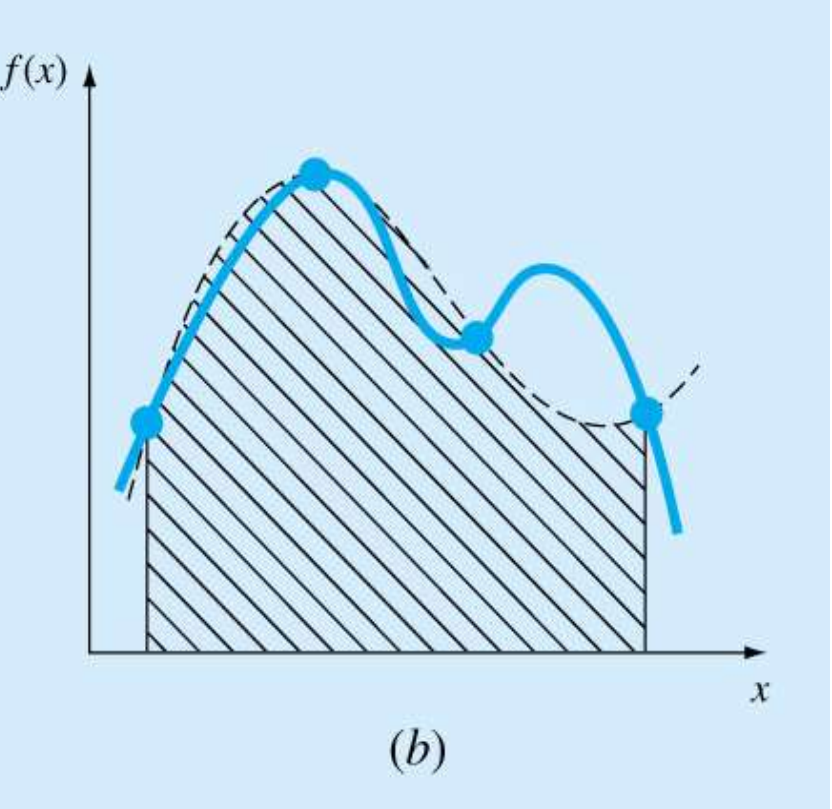
고차 보간다항식은 진동과 반올림오차로 인한 문제점이 있었다.
저차 보간 다항식을 사용하면 (a)처럼 중앙의 예측하려는 값의 오차가 커지고, 고차 보간 다항식을 사용하면 (c)처럼 중앙은 잘 예측을 하나, 가장자리의 오차가 커진다.
이를 해결하기 위해 다음의 방법을 사용할 수 있다.
저차 다항식 사용
저차에 맞게 보간 구역을 잘게 나누어 적용
이를 스플라인 보간법이라고 하며, (d)는 1차 스플라인 보간식을 적용한 상태이다.
2) 1차 (선형) 스플라인
( x i , f i ) , ( x i + 1 , f i + 1 ) , ( x i + 2 , f i + 2 ) (x_i, f_i), (x_{i+1}, f_{i+1}), (x_{i+2}, f_{i+2}) ( x i , f i ) , ( x i + 1 , f i + 1 ) , ( x i + 2 , f i + 2 )
S i S_i S i S i + 1 S_{i+1} S i + 1
S i ( x ) = a i + b i ( x − x i ) S_i(x) = a_i + b_i(x-x_i) S i ( x ) = a i + b i ( x − x i )
여기서 구해야하는 변수는 a i , b i a_i, b_i a i , b i
점이 n개면, n-1개의 구간이 나오고, 즉 스플라인이 n-1개가 있어야한다. 결국, 구해야하는 변수의 갯수는 2(n-1)개이다.
x = x i x=x_i x = x i S i = f i S_i = f_i S i = f i f i = a i f_i = a_i f i = a i
x = x i + 1 x=x_{i+1} x = x i + 1 S i = f i + 1 S_i = f_{i+1} S i = f i + 1 f i + 1 = f i + b i ( x i + 1 − x i ) f_{i+1} = f_i + b_i(x_{i+1}-x_i) f i + 1 = f i + b i ( x i + 1 − x i ) b i = f i + 1 − f i x i + 1 − x i b_i = {f_{i+1} - f_i \over x_{i+1}-x_i} b i = x i + 1 − x i f i + 1 − f i
따라서, ( x i , f i ) (x_i, f_i) ( x i , f i ) ( x i + 1 , f i + 1 ) (x_{i+1}, f_{i+1}) ( x i + 1 , f i + 1 ) S i ( x ) = f i + f i + 1 − f i x i + 1 − x i ( x − x i ) S_i(x) = f_i + {f_{i+1} - f_i \over x_{i+1}-x_i}(x-x_i) S i ( x ) = f i + x i + 1 − x i f i + 1 − f i ( x − x i )
이는 newton 선형 보간 다항식과 같은 형태이다.
18-2 2차, 3차 스플라인
1) 2차 스플라인(Quadratic Spline)
1차 스플라인 + 1차 도함수의 연속
x 2 x^2 x 2
S i ( x ) = a i + b i ( x − x i ) + c i ( x − x i ) 2 S_i(x) = a_i + b_i(x-x_i) + c_i(x-x_i)^2 S i ( x ) = a i + b i ( x − x i ) + c i ( x − x i ) 2 S i ′ ( x ) = b i + 2 c i ( x − x i ) S'_i(x) = b_i + 2c_i(x-x_i) S i ′ ( x ) = b i + 2 c i ( x − x i )
3(n-1)개의 미지수이기 때문에 3(n-1)개의 식을 찾아야한다.
x = x i x=x_i x = x i s i = f i s_i = f_i s i = f i f i = a i f_i = a_i f i = a i
x = x i + 1 x=x_{i+1} x = x i + 1 s i = f i + 1 s_i = f_{i+1} s i = f i + 1 f i + 1 = f i + b i h i + c i h i 2 f_{i+1} = f_i + b_ih_i + c_ih_i^2 f i + 1 = f i + b i h i + c i h i 2 h = x i + 1 − x i h=x_{i+1}-x_i h = x i + 1 − x i
x = x i + 1 x=x_{i+1} x = x i + 1 s i s_i s i s i ′ ( x ) = b i + 2 c i ( x − x i ) s'_i(x) = b_i + 2c_i(x-x_i) s i ′ ( x ) = b i + 2 c i ( x − x i ) s i + 1 ′ ( x ) = b i + 1 + 2 c i + 1 ( x − x i + 1 ) s'_{i+1}(x) = b_{i+1} + 2c_{i+1}(x-x_{i+1}) s i + 1 ′ ( x ) = b i + 1 + 2 c i + 1 ( x − x i + 1 ) s i ′ ( x i + 1 ) = s i + 1 ′ ( x i + 1 ) s'_i(x_{i+1}) = s'_{i+1}(x_{i+1}) s i ′ ( x i + 1 ) = s i + 1 ′ ( x i + 1 ) b i + 2 c i h i = b i + 1 b_i + 2c_ih_i = b_{i+1} b i + 2 c i h i = b i + 1
끝단 조건 (첫두접 직선 연결)s ′ ′ ( x 1 ) = 0 s''(x_1) = 0 s ′ ′ ( x 1 ) = 0 c 1 = 0 c_1=0 c 1 = 0
2차 스플라인은 첫번째 스플라인이 직선으로 나오고, 나머지 부분은 곡선으로 나온다. 이러한 점이 비대칭성을 보이기 때문에 잘 쓰이지 않는다.
2) 3차 스플라인(Cubic Splines)
2차 스플라인 + 2차 도함수 연속
S i ( x ) = a i + b i ( x − x i ) + c i ( x − x i ) 2 + d i ( x − x i ) 3 S_i(x) = a_i + b_i(x-x_i) + c_i(x-x_i)^2 + d_i(x-x_i)^3 S i ( x ) = a i + b i ( x − x i ) + c i ( x − x i ) 2 + d i ( x − x i ) 3 S i ′ ( x ) = b i + 2 c i ( x − x i ) + 3 d i ( x − x i ) 2 S'_i(x) = b_i + 2c_i(x-x_i) + 3d_i(x-x_i)^2 S i ′ ( x ) = b i + 2 c i ( x − x i ) + 3 d i ( x − x i ) 2 S i ′ ′ ( x ) = 2 c i + 6 d i ( x − x i ) S''_i(x) = 2c_i + 6d_i(x-x_i) S i ′ ′ ( x ) = 2 c i + 6 d i ( x − x i )
4(n-1)개 미지수 → 4(n-1)개의 식이 필요
x = x i x=x_i x = x i s i = f i s_i = f_i s i = f i f i = a i f_i = a_i f i = a i
x = x i + 1 x=x_{i+1} x = x i + 1 s i = f i + 1 s_i = f_{i+1} s i = f i + 1 f i + 1 = f i + b i h i + c i h i 2 + d i h i 3 f_{i+1} = f_i + b_ih_i + c_ih_i^2 + d_ih_i^3 f i + 1 = f i + b i h i + c i h i 2 + d i h i 3 h = x i + 1 − x i h=x_{i+1}-x_i h = x i + 1 − x i
x = x i + 1 x=x_{i+1} x = x i + 1 s i s_i s i s i ′ ( x i + 1 ) = s i + 1 ′ ( x i + 1 ) s'_i(x_{i+1}) = s'_{i+1}(x_{i+1}) s i ′ ( x i + 1 ) = s i + 1 ′ ( x i + 1 ) b i + 2 c i h i + 3 d i h i 2 = b i + 1 b_i + 2c_ih_i+3d_ih_i^2 = b_{i+1} b i + 2 c i h i + 3 d i h i 2 = b i + 1
x = x i + 1 x=x_{i+1} x = x i + 1 s i ′ ′ ( x i + 1 ) = s i + 1 ′ ′ ( x i + 1 ) s_i''(x_{i+1}) = s''_{i+1}(x_{i+1}) s i ′ ′ ( x i + 1 ) = s i + 1 ′ ′ ( x i + 1 ) 2 c i + 6 d i h i = 2 c i + 1 2c_i + 6d_ih_i = 2c_{i+1} 2 c i + 6 d i h i = 2 c i + 1
끝단 조건 (첫두접 직선 연결)s ′ ′ ( x 1 ) = 0 s''(x_1) = 0 s ′ ′ ( x 1 ) = 0 s n − 1 ′ ′ ( x n ) = 0 s''_{n-1}(x_n)=0 s n − 1 ′ ′ ( x n ) = 0
Runge 함수의 edge 에서도 오차가 적은 모습을 보여준다.
from scipy.interpolate import CubicSpline
cs = CubicSpline(x, y, bc_type='natural')19-1 사다리꼴 적분(The Trapezoidal Rule)
선형 보간식에 기초한 수치적분법
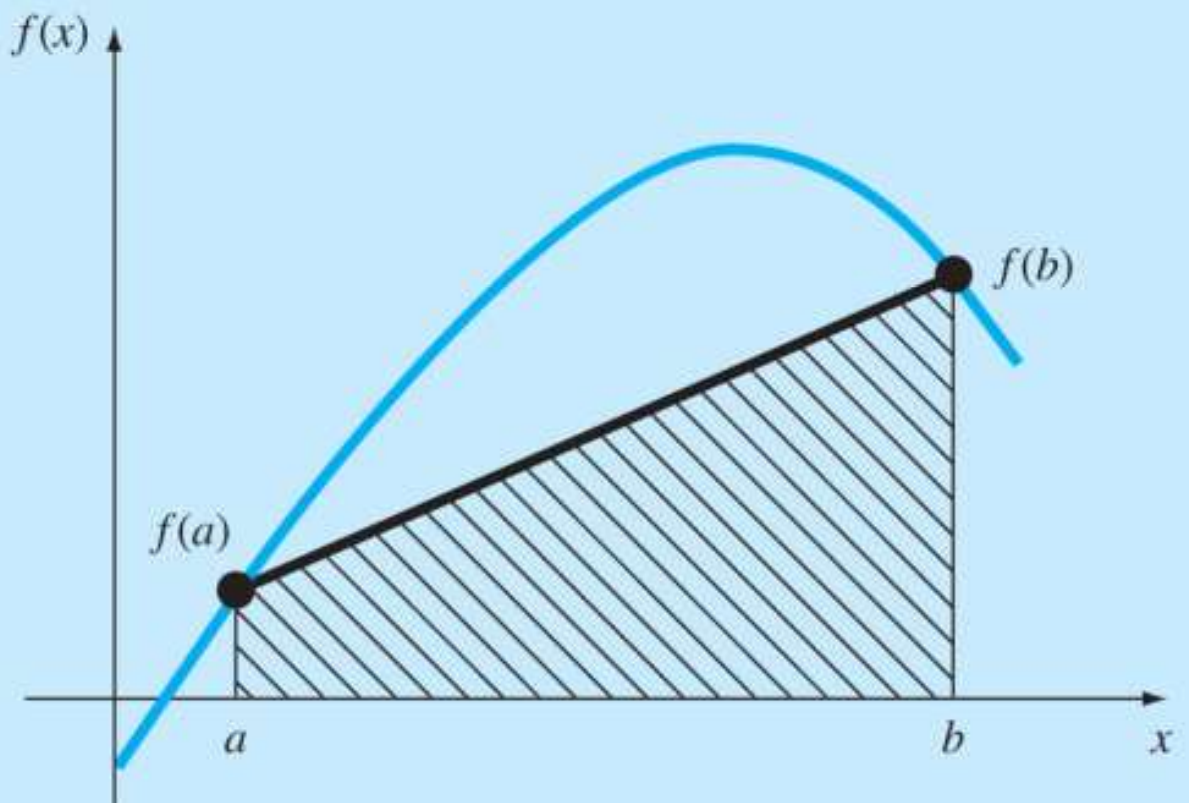
I = ∫ a b f ( x ) d x = b − a 2 ( f ( a ) + f ( b ) ) + E I = \int^b_af(x) dx = {b-a \over 2}(f(a)+f(b)) + E I = ∫ a b f ( x ) d x = 2 b − a ( f ( a ) + f ( b ) ) + E
E ( 오차 ) ∝ h 2 E(\text{오차}) \propto h^2 E ( 오차 ) ∝ h 2 E ≈ − b − a 12 h 2 f ˉ ′ ′ E \approx -{b-a\over 12}h^2\bar f'' E ≈ − 1 2 b − a h 2 f ˉ ′ ′
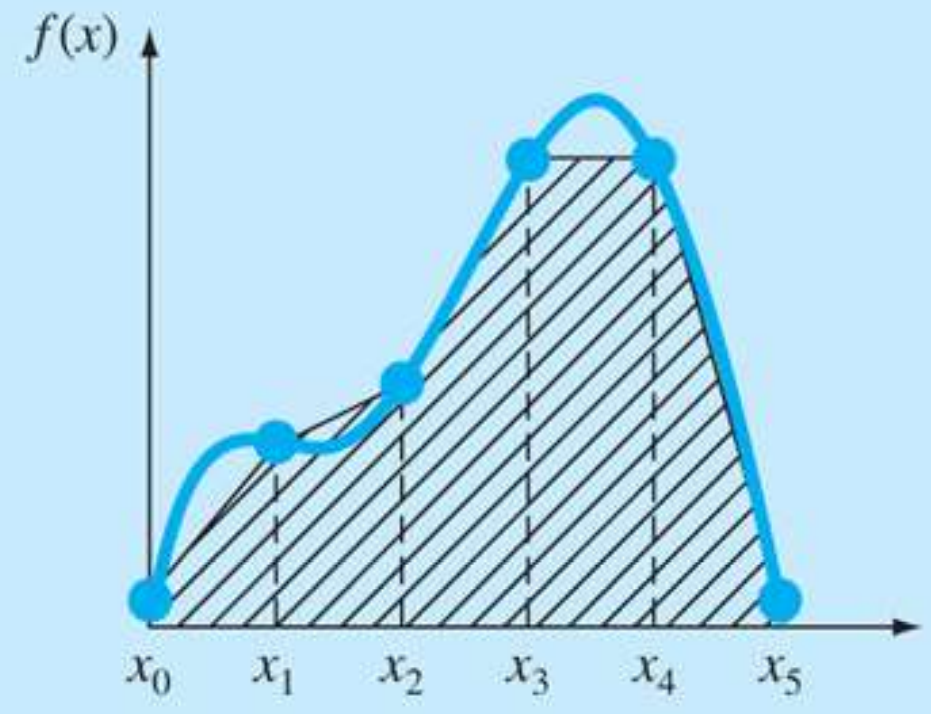
합성 사다리꼴 공식
오차를 줄이기 위해 적분 구간을 여러개로 나눠서 적분.
등간격 h의 n개 구간으로 나누어 적분하면, h = b − a n h = {b-a \over n} h = n b − a I = h 2 ( f 0 + f 1 ) + h 2 ( f 1 + f 2 ) + h 2 ( f 2 + f 3 ) + . . . + h 2 ( f n − 1 + f n ) I = {h\over2}(f_0+f_1) + {h\over2}(f_1+f_2) + {h\over2}(f_2+f_3) + ... + {h\over2}(f_{n-1}+f_n) I = 2 h ( f 0 + f 1 ) + 2 h ( f 1 + f 2 ) + 2 h ( f 2 + f 3 ) + . . . + 2 h ( f n − 1 + f n ) = h 2 ( f 0 + 2 f 1 + 2 f 2 + . . . + 2 f n − 1 + f n ) = {h \over 2}(f_0+2f_1 + 2f_2 + ... + 2f_{n-1} + f_n) = 2 h ( f 0 + 2 f 1 + 2 f 2 + . . . + 2 f n − 1 + f n )
각 f 계수가 0과 n만 1이고 나머지 2인 형태.
import numpy as np
def f(x):
return 1 - np.exp(-x)
def trapezoidalRule(a, b, n):
h = (b - a) / n
x = np.linspace(a, b, n+1)
I = f(x[0]) + f(x[-1])
for i in range(1, n):
I += 2 * f(x[i])
I *= h / 2
return I
print(trapezoidalRule(0, 4, 2))19-2 Simpson 적분
1) Simpson 1/3 적분
2차 보간다항식에 기초한 수치적분
I = 1 3 h ( f 0 + 4 f 1 + f 2 ) + E I = {1 \over 3}h(f_0 + 4f_1 + f_2) + E I = 3 1 h ( f 0 + 4 f 1 + f 2 ) + E
h = b − a 2 h = {b-a \over 2} h = 2 b − a f i = f ( x i ) = f ( a + i h ) f_i = f(x_i) = f(a + ih) f i = f ( x i ) = f ( a + i h )
E ∝ h 4 E \propto h^4 E ∝ h 4
합성 Simpson 1/3 법칙
짝수개 구간 영역에만 반복 적용 가능
I = h 3 ( f 0 + 4 f 1 + f 2 ) + h 3 ( f 2 + 4 f 3 + f 4 ) + . . . + h 3 ( f n − 2 + 4 f n − 1 + f n ) + E I = {h \over 3}(f_0 + 4f_1 + f_2) + {h \over 3} (f_2 + 4f_3 + f_4) + ... + {h \over 3}(f_{n-2}+4f_{n-1}+f_n) + E I = 3 h ( f 0 + 4 f 1 + f 2 ) + 3 h ( f 2 + 4 f 3 + f 4 ) + . . . + 3 h ( f n − 2 + 4 f n − 1 + f n ) + E
= h 3 ( f 0 + 4 f 1 + 2 f 2 + 4 f 3 + 2 f 4 + . . . + 2 f n − 2 + 4 f n − 1 + f n ) = {h \over 3}(f_0+4f_1 + 2f_2 + 4f_3 + 2f_4 + ... + 2f_{n-2} + 4f_{n-1} + f_n) = 3 h ( f 0 + 4 f 1 + 2 f 2 + 4 f 3 + 2 f 4 + . . . + 2 f n − 2 + 4 f n − 1 + f n )
양 끝 계수 1, 나머지 4, 2 반복
import numpy as np
def f(x):
return 1 - np.exp(-x)
def simpsons13(a, b, n):
h = (b - a) / n
x = np.linspace(a, b, n+1)
I = f(x[0]) + f(x[-1])
for i in range(1, n, 2):
I += 4 * f(x[i])
for i in range(2, n-1, 2):
I += 2 * f(x[i])
I *= h / 3
return I
print(simpsons13(0, 4, 4))2) Simpson 3/8 적분
3차 보간다항식에 기초한 수치적분
I = ∫ a b f ( x ) d x I = \int^b_af(x)dx I = ∫ a b f ( x ) d x = 3 8 h ( f 0 + 3 f 1 + 3 f 2 + f 3 ) + E = {3\over8}h (f_0 + 3f_1 + 3f_2 +f_3) + E = 8 3 h ( f 0 + 3 f 1 + 3 f 2 + f 3 ) + E
h = b − a 3 h = {b-a \over 3} h = 3 b − a f i = f ( x i ) = f ( a + i h ) f_i = f(x_i) = f(a+ih) f i = f ( x i ) = f ( a + i h ) E ∝ h 4 E \propto h^4 E ∝ h 4
합성 Simpson 3/8 적분
3의 배수개 구간에만 반복 적용 가능
I = 3 8 h ( f 0 + 3 f 1 + 3 f 2 + 2 f 3 + 3 f 4 + 3 f 5 + 2 f 6 + . . . ) + E I = {3\over8}h (f_0 + 3f_1 + 3f_2+ 2f_3 + 3f_4 + 3f_5 + 2f_6 + ... ) + E I = 8 3 h ( f 0 + 3 f 1 + 3 f 2 + 2 f 3 + 3 f 4 + 3 f 5 + 2 f 6 + . . . ) + E
양 끝 계수 1, 나머지는 3, 3, 2 패턴 반복
import numpy as np
def f(x):
return 1 - np.exp(-x)
def simpsons_38(a, b, n):
h = (b - a) / 3
x = np.linspace(a, b, n+1)
I = f(x[0]) + f(x[-1])
for i in range(1, n-1):
if i % 3 == 0:
I += 2*f(x[i])
else:
I += 3*f(x[i])
I *= (3/8)*h
return I
print(simpsons_38(0, 4, 6))3) 임의 갯수 구간 적분
짝수개 구간: 1/3 법칙 적용
3배수 구간: 3/8 법칙 적용
19-3 Newton-Cotes 적분
1) Newton-Cotes 폐구간 적분
사다리꼴, Simpson 1/3, Simpson 3/8 같은 적분 공식을 일반화한 적분 공식이다.
∫ a b f ( x ) d x = α h ( w 0 f 0 + w 1 f 1 + . . . + w n f n ) + E \int^b_af(x) dx = \alpha h (w_0f_0 + w_1f_1 + ... + w_nf_n) + E ∫ a b f ( x ) d x = α h ( w 0 f 0 + w 1 f 1 + . . . + w n f n ) + E
f n = f ( x n ) f_n = f(x_n) f n = f ( x n ) x n = a + n h x_n = a+nh x n = a + n h h = b − a n h = {b-a \over n} h = n b − a
w n w_n w n
즉, 사다리꼴, Simpson 1/3, Simpson 3/8 공식은 Newton-Cotes 의 특수예이다.
2) Newton-Cotes 개구간 적분
적분의 한계에서의 함수값을 알 수 없을 때 사용.
19-4 부등간격 적분 및 다중 적분
1) 부등간격 적분
부등간격 일 경우, 구간별로 사다리꼴 공식을 적용한다.
I = h 1 f 0 + f 1 2 + h 2 f 1 + f 2 2 + . . . + h n f n − 1 + f n 2 I = h_1 {f_0 + f_1 \over 2} + h_2 {f_1 + f_2 \over 2} + ... + h_n {f_{n-1} + f_n \over 2} I = h 1 2 f 0 + f 1 + h 2 2 f 1 + f 2 + . . . + h n 2 f n − 1 + f n
import numpy as np
def f(x):
return 0.2 + 25.*x - 200.*x**2 + 675.*x**3 - 900.*x**4 + 400.*x**5
def trapezoidalRule(a, b, n):
h = (b - a) / n
x = np.linspace(a, b, n+1)
I = f(x[0]) + f(x[-1])
for i in range(1, n-1):
I += 2 * f(x[i])
I *= h / 2
return I
def trapuneq(x, y):
n = len(x)
if len(y) != n:
return 'x and y arrays must be equal length'
s=0
for i in range(n-1):
if x[i+1] < x[i]:
return 'x array not in ascending order'
s += trapezoidalRule(x[i], x[i+1], 1)
return s
x = np.array([0.,0.12,0.22,0.32,0.36,0.4,0.44, 0.54,0.64,0.7,0.8])
y = f(x)
print(trapuneq(x, y))
2) 다중 적분
변수가 2개일 때 사용하는 적분법이다.
단순 수치적분을 x축과 y축에 대해 두번 적용한다.I = ∫ a b ( ∫ c d f ( x , y ) d y ) d x = ∫ c d ( ∫ a b f ( x , y ) d x ) d y I = \int^b_a (\int^{d}_{c}f(x, y)dy) dx = \int^d_c(\int^b_af(x, y)dx)dy I = ∫ a b ( ∫ c d f ( x , y ) d y ) d x = ∫ c d ( ∫ a b f ( x , y ) d x ) d y
CHAPTER 20 함수의 수치적분(Numerical Integration of Functions)
20-1 Romberg 적분법
1) Richardsm 외삽법
두 개의 적분값을 사용해 제 3의 더욱 정확한 적분값을 계산하는 방법
I = I ( h ) + E ( h ) I = I(h) + E(h) I = I ( h ) + E ( h )
간격 h1을 사용하면, I = I ( h 1 ) + E ( h 1 ) I = I(h_1) + E(h_1) I = I ( h 1 ) + E ( h 1 )
간격 h2을 사용하면, I = I ( h 2 ) + E ( h 2 ) I = I(h_2) + E(h_2) I = I ( h 2 ) + E ( h 2 )
이는 각각의 에러를 포함한 식이므로 둘은 같은 결과이다.
사다리꼴 공식에서 E ∝ h 2 E \propto h^2 E ∝ h 2
E ( h 1 ) E ( h 2 ) ≈ ( h 1 h 2 ) 2 {E(h_1) \over E(h_2)} \approx ({h_1 \over h_2})^2 E ( h 2 ) E ( h 1 ) ≈ ( h 2 h 1 ) 2
이를 정리하면
I ( h 1 ) + E ( h 2 ) ( h 1 h 2 ) 2 = I ( h 2 ) + E ( h 2 ) I(h_1) + E(h_2)({h_1 \over h_2})^2 = I(h_2) + E(h_2) I ( h 1 ) + E ( h 2 ) ( h 2 h 1 ) 2 = I ( h 2 ) + E ( h 2 ) E ( h 2 ) = I ( h 2 ) − I ( h 1 ) h 1 h 2 2 − 1 E(h_2) = {I(h_2)-I(h_1) \over {h_1\over h_2}^2 -1 } E ( h 2 ) = h 2 h 1 2 − 1 I ( h 2 ) − I ( h 1 )
→ I = I ( h 2 ) + I ( h 2 ) − I ( h 1 ) h 1 h 2 2 − 1 I = I(h_2) + {I(h_2)-I(h_1) \over {h_1\over h_2}^2 -1} I = I ( h 2 ) + h 2 h 1 2 − 1 I ( h 2 ) − I ( h 1 )
이 식은 사다리꼴 적분의 두 개의 결과(O ( h 2 ) O(h^2) O ( h 2 ) O ( h 4 ) O(h^4) O ( h 4 )
h 2 = h 1 2 h_2 = {h_1 \over 2} h 2 = 2 h 1 I = 4 3 I ( h 2 ) − 1 3 I ( h 1 ) I = {4 \over 3}I(h_2) - {1\over3}I(h_1) I = 3 4 I ( h 2 ) − 3 1 I ( h 1 )
h 2 = h 1 4 h_2 = {h_1 \over 4} h 2 = 4 h 1 I = 16 15 I m − 1 15 I e I = {16 \over 15}I_m - {1\over 15}I_e I = 1 5 1 6 I m − 1 5 1 I e O ( h 4 ) + O ( h 4 ) → O ( h 6 ) O(h^4) + O(h^4) \rarr O(h^6) O ( h 4 ) + O ( h 4 ) → O ( h 6 )
h 2 = h 1 8 h_2 = {h_1 \over 8} h 2 = 8 h 1 I = 64 63 I m − 1 63 I e I = {64 \over 63}I_m - {1\over 63}I_e I = 6 3 6 4 I m − 6 3 1 I e O ( h 6 ) + O ( h 6 ) → O ( h 8 ) O(h^6) + O(h^6) \rarr O(h^8) O ( h 6 ) + O ( h 6 ) → O ( h 8 )
I m I_m I m I e I_e I e
2) Romberg 적분법
Richardsm 외삽법을 효과적으로 구현하는 계산알고리즘을 Romberg 적분법으로 부른다.
I j , k = 4 k − 1 I j + 1 , k − 1 − I j , k − 1 4 k − 1 − 1 I_{j, k} = {4^{k-1}I_{j+1, k-1} - I_{j, k-1} \over 4^{k-1}-1} I j , k = 4 k − 1 − 1 4 k − 1 I j + 1 , k − 1 − I j , k − 1
k: 적분단계 index (k=1: O ( h 2 ) O(h^2) O ( h 2 ) O ( h 4 ) O(h^4) O ( h 4 ) O ( h 6 ) O(h^6) O ( h 6 )
∣ ϵ a ∣ = ∣ I 1 , k − I 2 , k − 1 I 1 , k ∣ < ϵ s |\epsilon_a| = |{I_{1,k} - I_{2,k-1} \over I_{1, k}}| < \epsilon_s ∣ ϵ a ∣ = ∣ I 1 , k I 1 , k − I 2 , k − 1 ∣ < ϵ s
import numpy as np
def f(x):
return 0.2 + 25.*x - 200.*x**2 + 675.*x**3 - 900*x**4 + 400*x**5
def trapezoidalRule(a, b, n):
h = (b - a) / n
x = np.linspace(a, b, n+1)
I = f(x[0]) + f(x[-1])
for i in range(1, n):
I += 2 * f(x[i])
I *= h / 2
return I
def romberg(a, b, es=1.e-8, maxit=30):
n = 1
I = np.zeros((2*maxit, maxit+1))
I[0, 0] = trapezoidalRule(a, b, n)
for iter in range(1, maxit+1):
n = 2**iter
I[iter, 0] = trapezoidalRule(a, b, n)
for k in range(1, iter+1):
j = iter-k
I[j, k] = (4**(k)*I[j+1, k-1] - I[j, k-1]) / (4**(k)-1)
ea = abs((I[0, iter]- I[1, iter-1]) / I[0, iter])
if ea <= es:
break
return I[0, iter] # ea < es 조건 만족 or maxit
print(romberg(0., 0.8))(index 처리로 인한 단순화된 구현)
20-2 Gauss-Legendre 구적법
적분점의 위치를 함수 내부의 적절한 위치로 옮기고, 이를 Gauss-Legendre 점이라고 함.
I ≈ c 0 f ( x 0 ) + c 1 f ( x 1 ) I \approx c_0f(x_0) + c_1f(x_1) I ≈ c 0 f ( x 0 ) + c 1 f ( x 1 ) 양의 와차와 음의 오차가 서로 상쇄되도록 하여 더욱 정확한 결과 도출
적분점이 부등간격
1) 특징
Legendre 점들은 Legendre 다항식의 근이고, 이를 사용한 수치적분법.
부등간격이기 때문에 해석적 함수를 적분하는데 더 유용함.
정확도가 Newton-Cotes 식보다 훨씬 높음.
2) 적분법
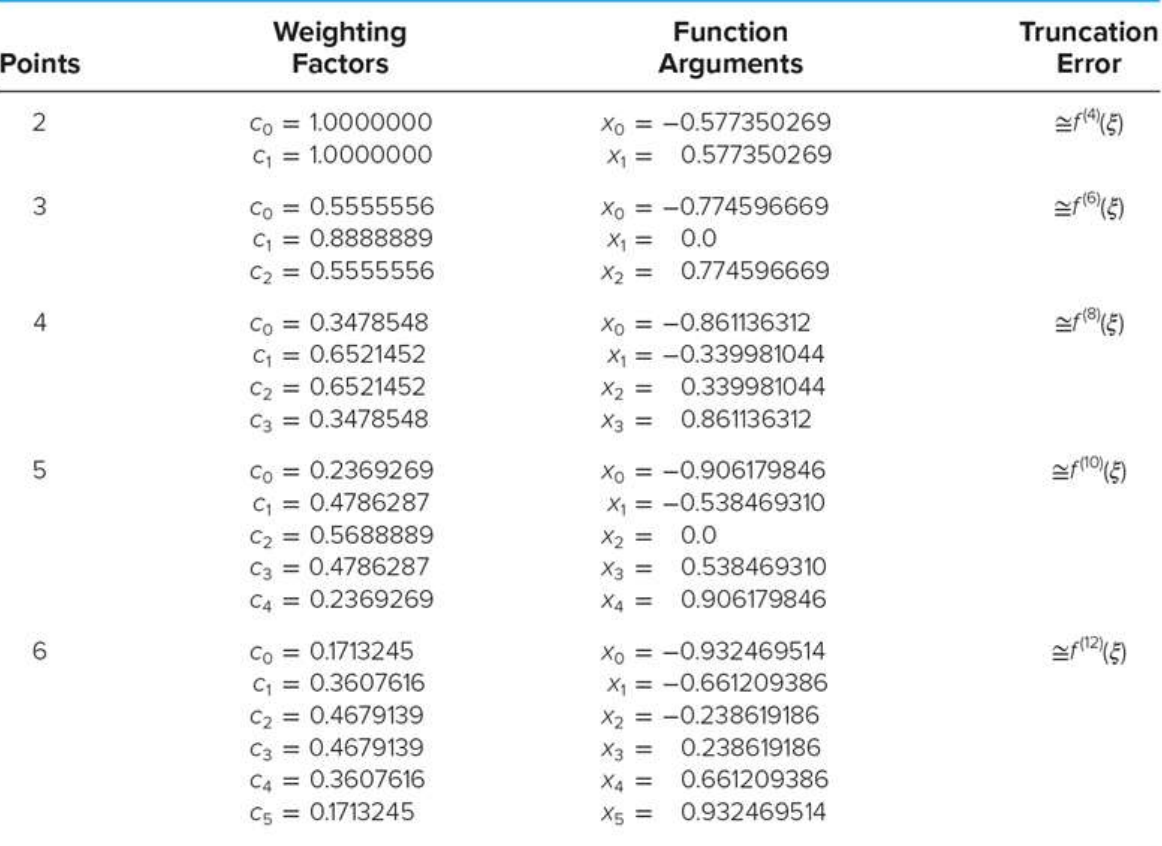
I = ∫ − 1 1 f ( x ) d x ≈ Σ k = 1 n = c k f ( x k ) I = \int^1_{-1}f(x)dx \approx \Sigma^{n}_{k=1} = c_kf(x_k) I = ∫ − 1 1 f ( x ) d x ≈ Σ k = 1 n = c k f ( x k )
n: Gauss 점의 갯수c k c_k c k x k x_k x k
이 -1 ~ 1까지인 표준 구간에서의 적분을 보는 방법이나, 이를 구간 mapping을 통해 임의의 a, b 구간에서도 성립하게끔 할 수 있다.
− 1 < x < 1 → a < z < b -1 < x < 1 \rarr a<z<b − 1 < x < 1 → a < z < b ∫ a b f ( z ) d z = b − a 2 Σ k = 1 n c k f ( z k ) \int^b_af(z)dz = {b-a\over 2} \Sigma^n_{k=1}c_kf(z_k) ∫ a b f ( z ) d z = 2 b − a Σ k = 1 n c k f ( z k ) z k = ( b − a ) x k + a + b 2 z_k = {(b-a)x_k + a + b\over 2} z k = 2 ( b − a ) x k + a + b
3) 장점
f(x)가 2n-1보다 작거나 같은 다항식일 때 정확
모든 가중치가 양의 값을 가지기에 반올림 오차의 발생 가능성이 낮다.
경계값이 적분에 포함되지 않기에 경계 부분에 특이점을 가져도 적분 가능.
import numpy as np
def f(x):
return np.exp(-x**2)
a, b = 0, 1.5
# Two-Point Gauss-Legendre Formula
def gauss_legendre_2pt(f, a, b):
weights = np.array([1., 1.])
args =np.array([-0.577350269, 0.577350269])
I = (b-a)/2 * np.sum(weights * f(((b-a)*args + a + b ) / 2))
return I
print("Two-Point Gauss-Legendre Formula")
print(gauss_legendre_2pt(f, a, b))
# Three-Point Gauss-Legendre Formula
def gauss_legendre_3pt(f, a, b):
weights = np.array([0.5555556, 0.8888889, 0.5555556])
args = np.array([-0.774596669, 0., 0.774596669])
I = (b-a)/2 * np.sum(weights * f(((b-a)*args + a + b ) / 2))
return I
print("Three-Point Gauss-Legendre Formula")
print(gauss_legendre_3pt(f, a, b))20-3 Adaptive Quadature
구간을 적응적으로 나누어 적분 정확도를 높이는 수치적분 기법
20-4 Monte Carlo Integration
함수의 적분값을 무작위 샘플링을 통해 근사적으로 계산하는 수치적분 기법
CHAPTER 21 수치미분(Numerical Differentiation)
21-1 고정확도 미분 공식 (유한차분근사)
테일러 급수 전개에서 더 많은 항을 포함시켜 더 정확한 수치미분 수행 가능.
1) Forward
2) Backward
3) Centered
import numpy as np
def f(x):
return np.sin(x)
x0 = np.pi / 4
h = np.pi / 12
# Forward Difference O(h)
def forward_difference_Oh(f, x, h):
return (f(x + h) - f(x)) / h
print("Forward Difference O(h)")
print(forward_difference_Oh(f, x0, h))
# Backward Difference O(h)
def backward_difference_Oh(f, x, h):
return (f(x) - f(x - h)) / h
print("Backward Difference O(h)")
print(backward_difference_Oh(f, x0, h))
# Forward Difference O(h^2)
def forward_difference_Oh2(f, x, h):
return (-3*f(x) + 4*f(x + h) - f(x + 2*h)) / (2*h)
print("Forward Difference O(h^2)")
print(forward_difference_Oh2(f, x0, h))
# Backward Difference O(h^2)
def backward_difference_Oh2(f, x, h):
return (3*f(x) - 4*f(x - h) + f(x - 2*h)) / (2*h)
print("Backward Difference O(h^2)")
print(backward_difference_Oh2(f, x0, h))
# Central Difference O(h^2)
def central_difference_Oh2(f, x, h):
return (f(x + h) - f(x - h)) / (2*h)
print("Central Difference O(h^2)")
print(central_difference_Oh2(f, x0, h))
# Central Difference O(h^4)
def central_difference_Oh4(f, x, h):
return (-f(x + 2*h) + 8*f(x + h) - 8*f(x - h) + f(x - 2*h)) / (12*h)
print("Central Difference O(h^4)")
print(central_difference_Oh4(f, x0, h))21-2 Richardson 외삽법
도함수값 개선 방안
간격 크기 줄이기
더 많은 점 포함하는 고차 공식 이용
Riochardson 외삽법에 기초해 두 도함수 계산값을 이용해 더 정확한 새로운 근사값을 구하는 방법.
D = 4 3 D ( h 2 ) − 1 3 D ( h 1 ) D = {4\over3}D(h_2) - {1\over3}D(h_1) D = 3 4 D ( h 2 ) − 3 1 D ( h 1 ) O ( h 2 ) O(h^2) O ( h 2 ) O ( h 4 ) O(h^4) O ( h 4 )
21-3 부등간격 도함수
유한 차분 근사나 Richardson 외삽법은 등간격 데이터가 주어져야 한다.
Lagrange 보간다항식으로 적합하여 부등간격 미분 가능.
인접한 세 점 ( x 0 , y 0 ) , ( x 1 , y 1 ) , ( x 2 , y 2 ) (x_0, y_0), (x_1, y_1), (x_2, y_2) ( x 0 , y 0 ) , ( x 1 , y 1 ) , ( x 2 , y 2 ) f ′ ( x ) = f ( x 0 ) 2 x − x 1 − x 2 ( x 0 − x 1 ) ( x 0 − x 2 ) + f ( x 1 ) 2 x − x 0 − x 2 ( x 1 − x 0 ) ( x 1 − x 2 ) + f ( x 2 ) 2 x − x 0 − x 1 ( x 2 − x 0 ) ( x 2 − x 1 ) f'(x) = f(x_0){2x - x_1 - x_2 \over (x_0 - x_1)(x_0 - x_2)} + f(x_1){2x - x_0-x_2\over (x_1-x_0)(x_1-x_2)} + f(x_2){2x - x_0 - x_1 \over (x_2-x_0)(x_2-x_1)} f ′ ( x ) = f ( x 0 ) ( x 0 − x 1 ) ( x 0 − x 2 ) 2 x − x 1 − x 2 + f ( x 1 ) ( x 1 − x 0 ) ( x 1 − x 2 ) 2 x − x 0 − x 2 + f ( x 2 ) ( x 2 − x 0 ) ( x 2 − x 1 ) 2 x − x 0 − x 1
이 도함수의 초정값은 중심차분과 같은 정확도를 갖는다. O ( h 2 ) O(h^2) O ( h 2 )
21-4 오차를 가지는 데이터에 대한 도함수와 적분
실험데이터는 오차를 포함할 수 있음.
수치미분은 데이터 내의 오차를 증폭시키는 경향이 있다.
부정확한 데이터에 대한 도함수를 구하는 접근법
21-5 편도함수 (Partial Derivatives)
등간격 데이터에서 중앙 차분으로 partial f' 구하기∂ f ∂ x = f ( x + Δ x , y ) − f ( x − Δ x , y ) 2 Δ x {\partial f \over \partial x} = {f(x+\Delta x, y) - f(x-\Delta x, y) \over 2\Delta x} ∂ x ∂ f = 2 Δ x f ( x + Δ x , y ) − f ( x − Δ x , y )
∂ f ∂ y = f ( x , y + Δ y ) − f ( x , y − Δ y ) 2 Δ y {\partial f \over \partial y} = {f(x,y +\Delta y) - f(x, y -\Delta y) \over 2\Delta y } ∂ y ∂ f = 2 Δ y f ( x , y + Δ y ) − f ( x , y − Δ y )
고차 미분을 위해 두 미분을 섞어서 구할 수 있다.∂ 2 f ∂ x ∂ y = ∂ ∂ x ( ∂ f ∂ y ) {\partial^2f \over \partial x \partial y} = {\partial \over \partial x}({\partial f\over \partial y}) ∂ x ∂ y ∂ 2 f = ∂ x ∂ ( ∂ y ∂ f )
= f ( x + Δ x , y + Δ y ) − f ( x + Δ x , y − Δ y ) − f ( x − Δ x , y + Δ y ) + f ( x − Δ x , y − Δ y ) 4 Δ x Δ y = {f(x+\Delta x, y + \Delta y) - f(x+ \Delta x,y - \Delta y) - f(x-\Delta x, y + \Delta y) + f(x - \Delta x,y - \Delta y) \over 4\Delta x \Delta y} = 4 Δ x Δ y f ( x + Δ x , y + Δ y ) − f ( x + Δ x , y − Δ y ) − f ( x − Δ x , y + Δ y ) + f ( x − Δ x , y − Δ y )
CHAPTER 22 초깃값 문제
상미분방정식(Ordinary Differential Equation, ODE)는 한 개 이상의 미지 함수와 그 함수의 도함수 사이의 관계를 나타내는 방정식이다. 상미분방정식은 미지 함수가 한 개의 독립 변수에만 의존하는 경우를 다룬다.
d y d t = f ( t , y ) {dy \over dt} = f(t, y) d t d y = f ( t , y ) 22-1 Runge-Kutta Methods (Introduction)
y i + 1 = y i + ϕ h y_{i+1} = y_i + \phi h y i + 1 = y i + ϕ h 새로운 값 = 기존 값 + 기울기 * Step size
y i y_i y i y i + 1 y_{i+1} y i + 1 h h h ϕ \phi ϕ
i의 단일 지점의 정보만을 기반으로 하기에 단일 구간 방법(One-Step Methods) 라고도 부른다.
단일 구간 방법은 모두 위의 식을 기반으로 하고, 더 정확한 예측을 위해 기울기의 추정되는 방식만 바뀐다.
22-2 Euler's Method
y i + 1 = y i + f ( t i , y i ) h y_{i+1} = y_i + f(t_i, y_i) h y i + 1 = y i + f ( t i , y i ) h ϕ = f ( t i , y i ) \phi = f(t_i, y_i) ϕ = f ( t i , y i ) f ( t i , y i ) f(t_i, y_i) f ( t i , y i )
여기서 새로 구해진 y 값은 다시 기울기를 추정하는데 다시 사용된다.
Euler's Method, 라고 불린다.
1) 오차 해석
절단 오차 (→ 전역절단오차(Global Truncation Error) = 구간절단 + 전파절단)
구간절단오차(Local Truncation Error): 단일 구간 적용 오차
전파절단오차(Propagated Truncation Error): 이전 구간에서 생성된 근사값이 다음 구간에 전파되며 생기는 오차
반올림 오차
테일러 급수 전개에서 오일러 방법을 유도하면 절단오차 크기와 속성에 대해 분석할 수 있음.
E t = f ′ ( t i , y i ) 2 ! h 2 + . . . + O ( h n + 1 ) E_t = {f'(t_i, y_i) \over 2!} h^2 + ... + O(h^{n+1}) E t = 2 ! f ′ ( t i , y i ) h 2 + . . . + O ( h n + 1 ) E t E_t E t
E a ≈ f ′ ( t i , y i ) 2 ! h 2 = O ( h 2 ) E_a \approx {f'(t_i, y_i) \over 2!} h^2 = O(h^2) E a ≈ 2 ! f ′ ( t i , y i ) h 2 = O ( h 2 ) E a E_a E a
전역오차(Global Truncation Error)는 계산이 반복되며 누적되어 O(h) 의 오차를 가진다.
1차 방법 이라고 부른다.
결론
전역오차는 구간 간격을 줄이면 감소
오일러 방법은 해가 1차식이라면 오차가 사라짐.
h의 값에 따라 오일러 방법은 조건적 안정성(Conditional Stability)를 가진 방법.
22-3 Heun's Method
예측-보정 방식(Predictor-Corrector Approach)으로 오일러 개선.
Predictor: y i + 1 0 = y i + f ( t i , y i ) h y^0_{i+1} = y_i + f(t_i, y_i)h y i + 1 0 = y i + f ( t i , y i ) h y i + 1 = y i + f ( t i , y i ) + f ( t i + 1 , y t + 1 0 ) 2 h y_{i+1} = y_i + {f(t_i, y_i)+f(t_{i+1}, y^0_{t+1}) \over 2}h y i + 1 = y i + 2 f ( t i , y i ) + f ( t i + 1 , y t + 1 0 ) h
초기에는 오일러 방법을 사용해 Predictor Equation으로 추정한다. 최종적으로 시작점과 끝점의 기울기 평균값으로 다시 보정하여 Corrector Eqaution으로 추정한다.
∣ ϵ a ∣ = ∣ y i + 1 j − y i + 1 j − 1 y i + 1 j ∣ 100 % |\epsilon_a| = |{y^j_{i+1} - y^{j-1}_{i+1} \over y^j_{i+1}}| 100\% ∣ ϵ a ∣ = ∣ y i + 1 j y i + 1 j − y i + 1 j − 1 ∣ 1 0 0 % y i + 1 j , y i + 1 j − 1 y^j_{i+1}, y^{j-1}_{i+1} y i + 1 j , y i + 1 j − 1
2차 방법이라고 부른다.
local error: O ( h 3 ) O(h^3) O ( h 3 ) O ( h 2 ) O(h^2) O ( h 2 )
22-4 Midpoint Method
구간의 중간 점에서 기울기 예측하여 오일러 개선
y i + 1 = y t + f ( t i + 1 / 2 , , y i + 1 / 2 ) h y_{i+1} = y_t + f(t_{i+1/2,}, y_{i+1/2})h y i + 1 = y t + f ( t i + 1 / 2 , , y i + 1 / 2 ) h
Newton-Cotes 적분 기반∫ t i t i + 1 f ( t ) d t ≊ h f ( t i + 1 / 2 ) \int^{t_{i+1}}_{t_i}f(t)dt \approxeq hf(t_{i+1/2}) ∫ t i t i + 1 f ( t ) d t ≊ h f ( t i + 1 / 2 )
구간오차: O ( h 3 ) O(h^3) O ( h 3 ) O ( h 2 ) O(h^2) O ( h 2 )
오일러 방법보다 더 적은 오차.
Improved Polygon Method라고도 불림.
22-5 Runge-Kutta Methods
더 높은 도함수를 도입하지 않고도 테일러 급수 방식의 고차항에 해당하는 정확도를 달성할 수 있는 방법.
y i + 1 = y i + ϕ h y_{i+1} = y_i + \phi h y i + 1 = y i + ϕ h ϕ = a 1 k 1 + a 2 k 2 + . . . + a n k n \phi = a_1k_1 + a_2k_2 + ... + a_nk_n ϕ = a 1 k 1 + a 2 k 2 + . . . + a n k n a i a_i a i k 1 = f ( t i , y i ) k_1 = f(t_i, y_i) k 1 = f ( t i , y i ) k 2 = f ( t i + p 1 h , y i + q 11 k 1 h ) k_2 = f(t_i + p_1h, y_i + q_{11}k_1h) k 2 = f ( t i + p 1 h , y i + q 1 1 k 1 h ) k 3 = f ( t i + p 2 h , y i + q 21 k 1 h + q 22 k 2 h ) k_3 = f(t_i + p_2h, y_i + q_{21}k_1h + q_{22}k_2h) k 3 = f ( t i + p 2 h , y i + q 2 1 k 1 h + q 2 2 k 2 h ) k n = f ( t i + p n − 1 h , y i + q n − 1 , 1 k 1 h + q n − 1 , 2 k 2 h + . . . + q n − 1 , n − 1 k n − 1 h ) k_n = f(t_i + p_{n-1}h, y_i + q_{n-1, 1}k_1h + q_{n-1,2}k_2h + ... + q_{n-1, n-1}k_{n-1}h) k n = f ( t i + p n − 1 h , y i + q n − 1 , 1 k 1 h + q n − 1 , 2 k 2 h + . . . + q n − 1 , n − 1 k n − 1 h )
p, q는 오차를 최소화하는 상수로 고정.
n값을 바꿔 오차의 최소 차수와 a, p, q 값이 달라진다.
n=1) 전역오차: O(h) (= 오일러 방법)
1) 2차 RK 방법
y i + 1 = y i + a 1 k 1 + a 2 k 2 h y_{i+1} = y_i + a_1k_1 + a_2k_2 h y i + 1 = y i + a 1 k 1 + a 2 k 2 h k 1 = f ( t i , y i ) k_1 = f(t_i, y_i) k 1 = f ( t i , y i ) k 2 = f ( t i + p 1 h , y i + q 11 k 1 h ) k_2 = f(t_i + p_1h, y_i + q_{11}k_1h) k 2 = f ( t i + p 1 h , y i + q 1 1 k 1 h )
a 1 + a 2 = 1 a_1 + a_2 = 1 a 1 + a 2 = 1 a 2 p 1 = 1 2 a_2p_1 = {1\over2} a 2 p 1 = 2 1 a 2 q 11 = 1 2 a_2q_{11} = {1 \over 2} a 2 q 1 1 = 2 1
외부의 값 하나 더 필요. 이 때의 널리 사용되는 RK2 방법들은 아래와 같다.
한 개의 수정자를 가진 Heun 방법 (a 2 = 1 2 a_2 = {1 \over 2} a 2 = 2 1
a 1 = 1 2 , p 1 = q 11 = 1 a_1 = {1 \over 2}, p_1 = q_{11} = 1 a 1 = 2 1 , p 1 = q 1 1 = 1
y i + 1 = y i + 1 2 k 1 + 1 2 k 2 h y_{i+1} = y_i + {1 \over 2}k_1 + {1 \over 2}k_2 h y i + 1 = y i + 2 1 k 1 + 2 1 k 2 h k 1 = f ( t i , y i ) k_1 = f(t_i, y_i) k 1 = f ( t i , y i ) k 2 = f ( t i + h , y i + k 1 h ) k_2 = f(t_i +h, y_i + k_1h) k 2 = f ( t i + h , y i + k 1 h )
중간점 방법(a 2 = 1 a_2 = 1 a 2 = 1
a 1 = 0 , p 1 = q 11 = 1 2 a_1 = 0, p_1=q_{11}= {1 \over 2} a 1 = 0 , p 1 = q 1 1 = 2 1
y i + 1 = y i + k 2 h y_{i+1} = y_i +k_2h y i + 1 = y i + k 2 h k 1 = f ( t i , y i ) k_1 = f(t_i, y_i) k 1 = f ( t i , y i ) k 2 = f ( t i + 1 2 h , y i + 1 2 k 1 h ) k_2 = f(t_i + {1 \over 2}h, y_i + {1 \over 2}k_1h) k 2 = f ( t i + 2 1 h , y i + 2 1 k 1 h )
Ralston 방법 (a 2 = 3 4 a_2 = {3 \over 4} a 2 = 4 3
a 1 = 1 4 , p 1 = q 11 = 2 3 a_1 = {1 \over 4}, p_1 = q_{11} = {2 \over 3} a 1 = 4 1 , p 1 = q 1 1 = 3 2
y i + 1 = y i + 1 4 k 1 + 3 4 k 2 h y_{i+1} = y_i + {1 \over 4}k_1 + {3 \over 4}k_2 h y i + 1 = y i + 4 1 k 1 + 4 3 k 2 h k 1 = f ( t i , y i ) k_1 = f(t_i, y_i) k 1 = f ( t i , y i ) k 2 = f ( t i + 2 3 h , y i + 2 3 k 1 h ) k_2 = f(t_i + {2 \over 3}h, y_i + {2 \over 3}k_1h) k 2 = f ( t i + 3 2 h , y i + 3 2 k 1 h )
이 방법이 절단 오차를 낮추기 위한 성능이 좋음.
2) 고전적 4차 RK 방법
보편적으로 쓰이는 4차 RK 방식.
y i + 1 = y i + 1 6 ( k 1 + 2 k 2 + 2 k 3 + k 4 ) h y_{i+1} = y_i + {1\over6}(k_1 + 2k_2 + 2k_3 + k_4 )h y i + 1 = y i + 6 1 ( k 1 + 2 k 2 + 2 k 3 + k 4 ) h k 1 = f ( t i , y i ) k_1 = f(t_i, y_i) k 1 = f ( t i , y i ) k 2 = f ( t i + 1 2 h , y i + 1 2 k 1 h ) k_2 = f(t_i + {1\over2}h, y_i + {1\over2}k_1h) k 2 = f ( t i + 2 1 h , y i + 2 1 k 1 h ) k 3 = f ( t i + 1 2 h , y i + 1 2 k 2 h ) k_3 = f(t_i + {1\over2}h, y_i + {1\over2}k_2h) k 3 = f ( t i + 2 1 h , y i + 2 1 k 2 h ) k 4 = f ( t i + h , y i + k 3 h ) k_4 = f(t_i + h, y_i + k_3h) k 4 = f ( t i + h , y i + k 3 h )
3) Butcher's 5차 RK 방법
O ( h 5 ) O(h^5) O ( h 5 )

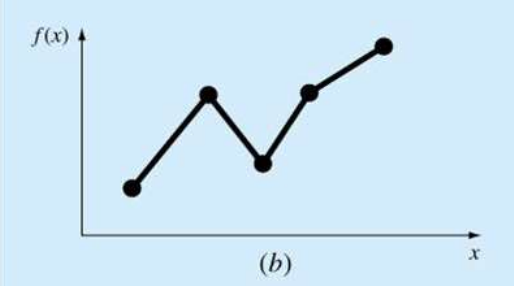
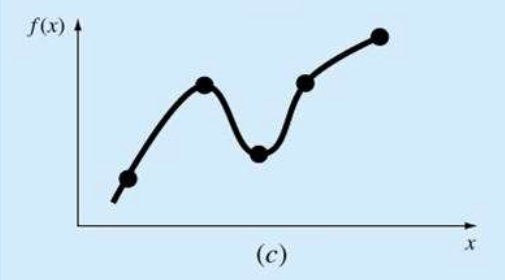
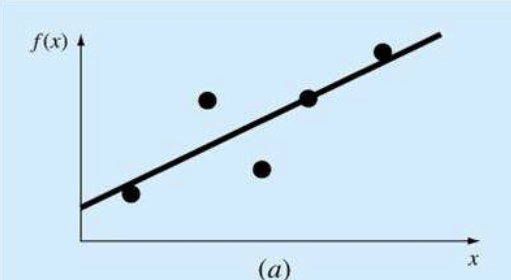
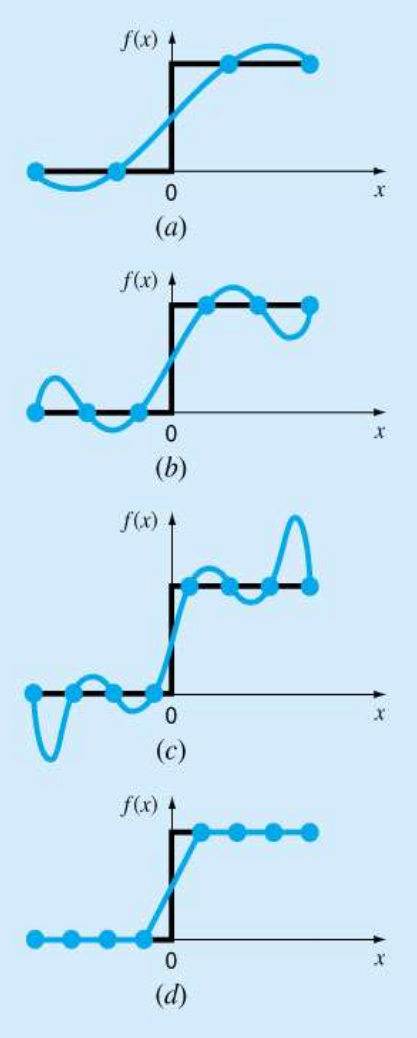 저차 보간 다항식을 사용하면 (a)처럼 중앙의 예측하려는 값의 오차가 커지고, 고차 보간 다항식을 사용하면 (c)처럼 중앙은 잘 예측을 하나, 가장자리의 오차가 커진다.
저차 보간 다항식을 사용하면 (a)처럼 중앙의 예측하려는 값의 오차가 커지고, 고차 보간 다항식을 사용하면 (c)처럼 중앙은 잘 예측을 하나, 가장자리의 오차가 커진다.