
참고자료
- Chapra의 파이썬 수치해석
- 순천향대학교 기계공학과 이상욱 교수님 수치해석 강의 영상
- 한양대학교 ERICA 2024-2 홍규연 교수님의 수치해석 강의
서론
-
제가 정리하는 수치해석에서 삽입되어 있는 코드는 책에 있는 코드가 불필요한 부분이 많고 직관적이지 않다고 판단했기에 정의에 기반하여 임의로 수정했음을 미리 밝힙니다.
-
제가 사전에 이미 공부한 내용이여서 정리하지 않은 내용도 있으므로 수치해석학 책의 모든 내용을 정리한 것은 아닙니다.
-
순서를 매긴 번호가 책의 챕터랑 일치하지 않습니다.
CHAPTER 4 반올림오차와 절단오차
4-1 정확도와 정밀도
정확도(Accuracy): 계산값이 얼마나 참값과 가까운지
정밀도(Precision): 계산값들이 얼마나 밀집되어 있는지

4-2 오차
1) 오차 수식 정리
: 유효 숫자에 관한 상대 오차.
즉, 이 만족하는 경우, 유효숫자가 n자리 보다 많아지면 종료할 수 있는 종료 조건임을 뜻한다.
2) 테일러 급수(Tayler Series)
함수 가 a에서 무한번 미분 가능할 때, 다음과 같다.
a=0일 때의 테일러 급수를 매클로린 급수(Maclaurin series)라고 부른다.
3) 반올림 오차(Roundoff Errors)
컴퓨터 숫자 표현의 한계로 숫자를 정확히 표현할 수 없어 생기는 오차.

- underflow: 부동소수점으로 표현된 숫자가 너무 작아져서 표현할 수 없는 현상.
- overflow: 부동소수점으로 표현된 숫자가 너무 커져서 표현할 수 없는 현상
Machine Epsilon(eps): 1과 1 바로 위의 실수 사이의 간격.
즉, 표현할 수 있는 가장 작은 숫자
4) 절단 오차(Truncation Errors)
정확한 수학적 과정을 대체하여 근사치를 사용하는 과정에서 발생하는 오차.
테일러 급수의 경우, 무한한 항과 무한한 미분이 필요하므로 일정한 구간에서 절단하게 된다. 이 과정에서 절단된 부분 만큼 오차가 발생하게 된다.
라고 하면, 다음과 같이 표현할 수 있다.
여기서 우리는 더 많은 항을 사용할 수록 절단되는 오차가 적으므로 더 정확도가 높은 근사치를 얻게 된다.
Zero-order(하나의 항) < First-order < Second-order(세개의 항) < ...
컴퓨터는 기본 산술 논리 연산 밖에 할 수 없어서 정확한 미분을 하지 못한다. 따라서, 테일러 급수를 통해서 다음과 같이 함수의 미분의 근사치를 구할 수 있다.
5) 전방 차분(Forward difference)
일 때,
truncation error = O(h)
6) 후방 차분(Backward difference)
일 때,
-
-
| (+, -, +, -, ...)
-
-
truncation error = O(h)
7) 중앙 차분(Centered difference)
일 때,
truncation error =
→ 중앙 차분의 오차가 적다.
8) 결론
결론적으로, 전체적인 오차를 줄이기 위해서는 Truncation error 와 Round-off Error를 합한 값이 최소가 되어야 한다. round off error 를 줄이기 위해서는 유효 숫자를 증가시켜야 하고, Truncation error 을 줄이기 위해서는 step size인 h()를 줄여야 한다.
step size를 계속 줄일 경우, 표현 자리가 부족하여 round off error 가 발생해 오차가 커질 것이고, step size가 커지면 truncation error 가 점점 커지므로 오차가 커질 것이다.
9) 수치 미분 구현
def forward_difference(f, x):
h = 1e-4
return (f(x+h) - f(x)) / h
def backward_difference(f, x):
h = 1e-4
return (f(x) - f(x-h)) / h
def centered_difference(f, x):
h = 1e-4 # 0.001
return (f(x+h) - f(x-h)) / (2*h)
def f(x):
return 2*x**2 + 3*x + 1
def fp(x):
return 4*x + 3
print("Truncation Errors(+ round-off)")
print("Forward_difference:", fp(1)-forward_difference(f, 1))
print("Backward_difference:", fp(1)-backward_difference(f, 1))
print("centered_difference:", fp(1)-centered_difference(f, 1))CHAPTER 5 근: 구간법 (Roots: Bracketing Methods)
5-1 Graphical Methods
그래프를 그려서 x축과 교차하는 지점 찾기.
함수가 연속적일 때 다음을 만족한다.
- 두 지점의 함수 값을 곱한 값이 음수이면, 이 두 지점 사이에 근이 홀수개가 존재한다.
- 두 지점의 함수 값을 곱한 값이 양수이면, 두 지점 사이에 0개 혹은 짝수개가 존재한다.
예외적으로, 두 지점 함수 값을 곱한 값이 음수이고, 함수가 연속적임에도 구간안에 중근이 있는 등의 경우에 홀수개가 아닐 수 있다.
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return -x**4 + 4*x**2 - 2
x = np.arange(-2.1, 2.1, 0.01)
y = f(x)
yz = np.zeros(x.shape[0])
plt.plot(x, y)
plt.plot(x, yz)
plt.show()5-2 이분법(The Bisection Method)
- 이 성립하는 과 를 찾는다.
- ()
()
()
근을 찾지 못했으면 2번으로 돌아간다.
이진 탐색과 동일한 알고리즘. 계속 반을 나누어가며 찾는 과정.
종료 조건의 구성
1. 근을 찾을 때까지 반복한다.
2. 으로 근사치를 구한다.
3. max_iteration(fixed number)을 지정해서 근사치를 구한다.
4. 사전의 목표 오차에 적정한 iteration인 n을 구한다.
()
여기서, 이고, 는 사전에 설정된 목표오차(a desired spectification for the error) 이다.
이분법은 xu와 xl이 얼마나 떨어졌는지와 상관없이 일정히 반으로 나눠서 찾아가기 때문에 확실하지만, 비효율적인 방법이다.
def f(x):
return (-2.75)*(x**3) + 18*(x**2) - 21*x - 12
def bisectionMethod(f, xl, xu, xm, es = 10**(-4), i=1):
if f(xl)*f(xu) > 0:
return '구간 안에 근이 존재하는지 확실치 않음.'
if f(xm) * f(xl) < 0:
xu = xm
else:
xl = xm
root = (xl+xu)/2
ea = abs((root - xm) / root)
print("%d:"%i, root)
if ea < es:
return root
return bisectionMethod(f, xl, xu, root, i=i+1)
xl = -3
xu = 10
print("The Bisection Method")
print(bisectionMethod(f, xl, xu, (xl+xu)/2))5-3 가위치법(The False-Position Method)
보간 방법(interpolation method)으로도 불림.
선형 보간법을 이용해 구간을 분할하여 찾아가기 때문에 이분법보다 훨씬 빠르게 수렴한다.
- (xu, f(xu))와 (xl, f(xl))을 잇는 직선의 x축과 교점이 되는 좌표가 (xr, f(xr))이 된다.
- f(xu)f(xr) <= 0 → xl = xr
f(xu)f(xr) > 0 → xu = xr - 종료 조건이 될 때까지 반복.
xu = c, xl = a로 두면 다음과 같이 간단히 정리할 수 있다.
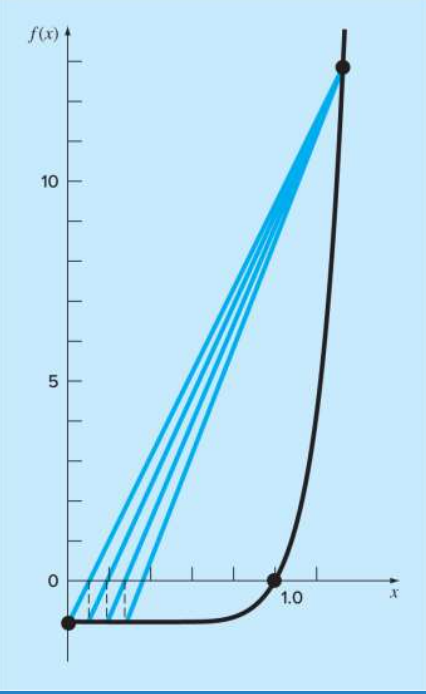
해당 경우는 가위치법이 좋지 않은 성능을 보여준다.
def f(x):
return (-2.75)*(x**3) + 18*(x**2) - 21*x - 12
def falsePositionMethod(f, xu, xl, es, i=1):
xr = (xl*f(xu) - xu*f(xl)) / (f(xu) - f(xl))
print("%d:" %i, xr)
if f(xu)*f(xr) <= 0:
xl = xr
else:
xu = xr
ea = abs((xu-xl) / xl)
if ea < es:
return xr
return falsePositionMethod(f, xu, xl, es, i=i+1)
print("The False-Position Method")
print(falsePositionMethod(f, 0, 2, 0.0001))CHAPTER 6 근: 개방법
6-1 단순 고정점 반복법(Simple Fixed-point Iteration)
형태로 식을 표현하여 계산값을 연속 대입하여 수렴시킨다.
이는
두 식의 교점을 구하는 것과 같다.
- 초기추정치 설정
- = g()로 결정.
- 중단조건 검사
2~3번 반복.
장점: g(x) 결정의 융통성, 방법의 단순성
단점: 때만 수렴, 같은 식이라도 g(x)을 어떻게 두냐에 따라 수렴 할 수도, 발산할 수도 있다.
: 점진적 수렴
: 진동 수렴
: 발산

import numpy as np
def f(x):
return 7*np.sin(x)*np.exp(-x) - 1
def g(x):
return -np.log(1 / (7*(np.sin(x))))
def simpleFixedPointIteration(g, xold, es=0.001, i=1):
xnew = g(xold)
print("%i:"%i, xnew)
ea = abs((xnew-xold) / xnew)
if ea < es:
return xnew
return simpleFixedPointIteration(g, xnew, i=i+1)
print("Simple Fixed-point Iteration")
print(simpleFixedPointIteration(g, 1))6-2 The Wegstein Method
단순 고정점 반복법 같이 x = g(x)의 식을 세우고, 두 점의 직선을 y=x 직선과 두 점을 지나는 직선과의 교점을 구한다. 이 교점이 세로운 x이고, 이를 반복하여 근으로 수렴하는 기법이다.
-
초기 가정값 와 을 정의한다. 이 두 초기값은 근을 포함할 필요가 없다.
-
-
중단조건 검사
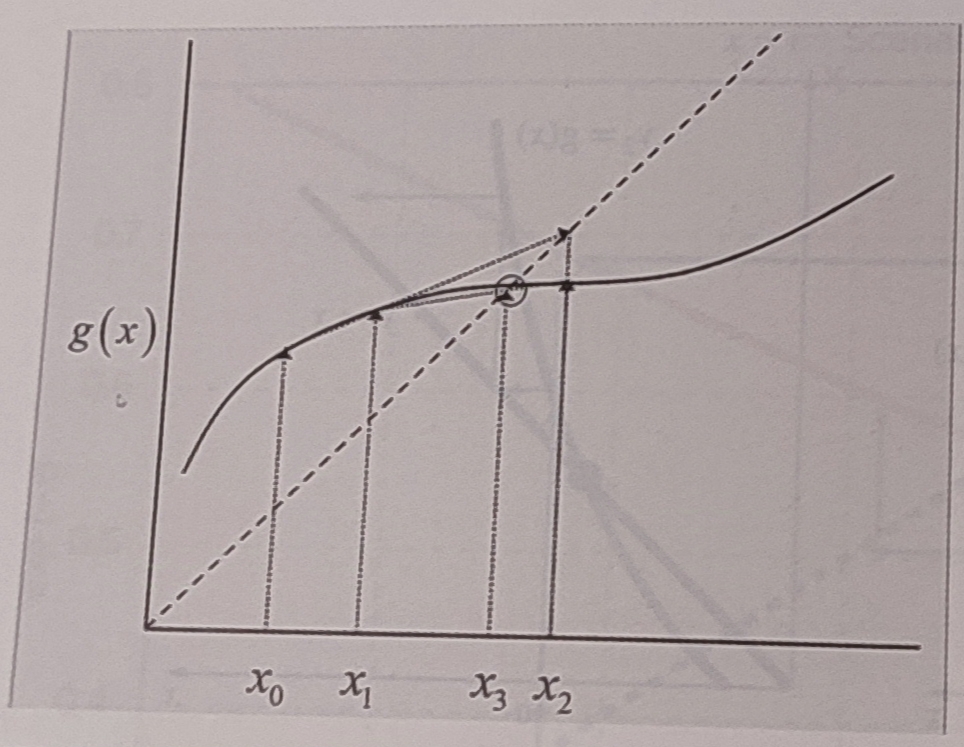
import numpy as np
def f(x):
return 7*np.sin(x)*np.exp(-x) - 1
def g(x):
return -np.log(1 / (7*(np.sin(x))))
def wegsteinMethod(g, xold, xpresent, es=0.0001, i=1):
xnew = (xpresent*g(xold) - xold*g(xpresent)) / ((xpresent-xold) - g(xpresent) + g(xold))
print("iter%d:"%i, xnew)
ea = abs((xnew-xpresent) / xnew)
if ea < es:
return xpresent
return wegsteinMethod(g, xpresent, xnew, i=i+1)
print("The Wegstein Method")
print(wegsteinMethod(g, 0.1, 0.2))6-3 뉴튼-랩슨법(Newton-Raphson Method)
초기근사값을 알고 있을 때 접선을 사용해 수렴시키는 방법.
즉, 근이 있는 곳을 대략적으로 파악하고 있어야 하고, 미분이 요구된다.
-
초기치 선택
-
f(x)=0을 1차까지 Taylor 전개하면
이를 정리하면,
이를 일반화하면,
-
계산 중단 조건 만족시 break.
2~3 반복
장점
매우 빠른 수렴 속도.
단점
수렴이 안되거나 수렴이 느린 경우가 존재한다.
-
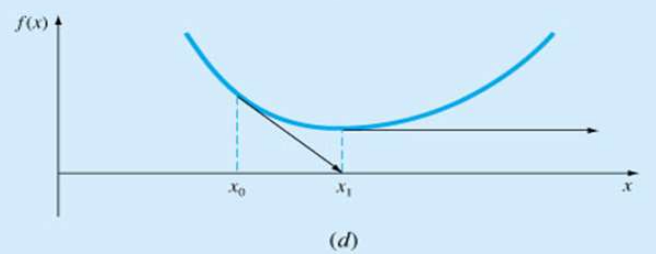
수렴이 느린 경우
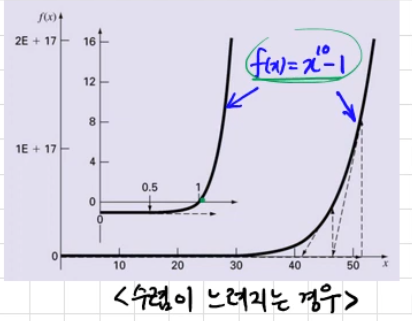
-
근이 변곡점 근처에 있는 경우
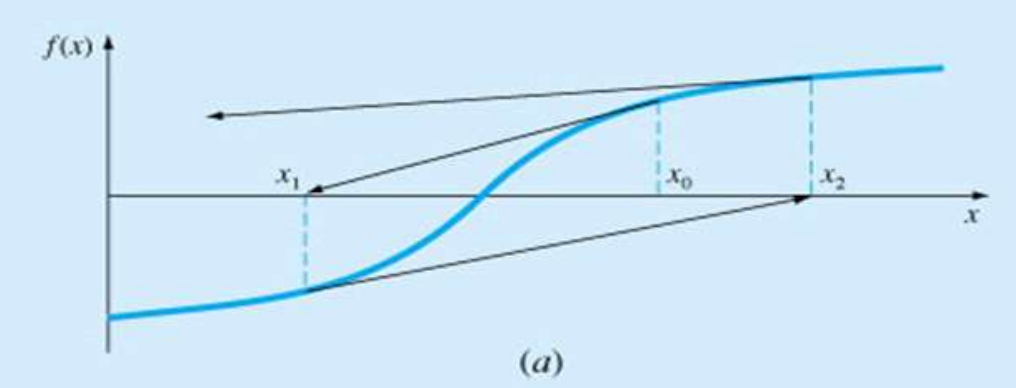
-
국부최소값 근처에서 진동하는 경우
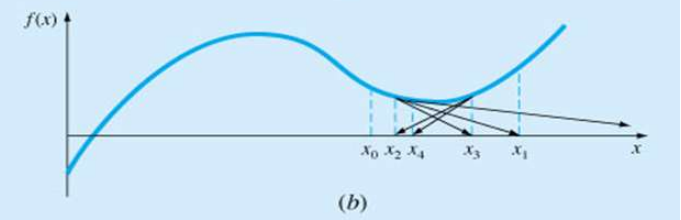
-
찾으려던 근이 아닌 다른 근을 찾아가는 경우
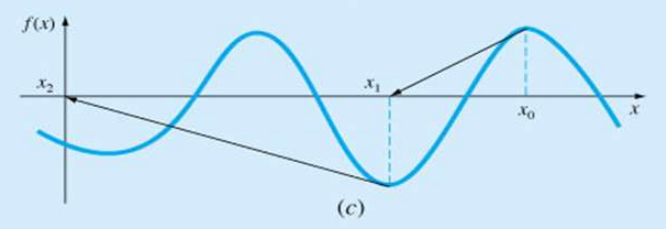
-
접선이 수평인 경우(기울기가 0인 경우)
따라서, 근 근처까지는 이분법 등의 다른 기법으로 근 근처까지 접근하고, 근처에서 뉴튼-랩슨법을 많이 사용한다.
import numpy as np
def f(x):
return 7*np.sin(x)*np.exp(-x) - 1
def fp(x):
return (7*np.exp(-x)) * (np.cos(x) - np.sin(x))
def newtonRaphsonMethod(f, xold, es=0.0001, i=1):
xnew = xold - (f(xold)/fp(xold))
print("iter %d:"%(i+1), xnew)
ea = abs((xnew - xold) / xnew)
if ea < es:
return xnew
return newtonRaphsonMethod(f, xnew, i=i+1)
print("Newton-Raphson Method")
print(newtonRaphsonMethod(f, 0.3))6-4 할선법(Secant Methods)
뉴튼-랩슨법과 다르게 도함수를 못구하는 경우에 사용할 수 있는 기법이다.
뉴튼-랩슨법의 f'(x)를 2개의 연속적인 반복값을 이용하여 근사한다.
따라서, 초기 추정치가 2개이다.
- 초기 추정치 2개
- 을 지나는 직선과 x축과의 교점인 를 구한다.
일반화하면, - 계산중단조건에 만족하면 break.
2~3 반복.
import numpy as np
def f(x):
return 7*np.sin(x)*np.exp(-x) - 1
def secantMethods(f, xold, xpresent, es=0.0001, i=1):
xnew = xpresent - f(xpresent)*((xold-xpresent)/(f(xold)-f(xpresent)))
print("%d:"%i, xnew)
ea = abs((xnew - xpresent) / xnew)
if ea < es:
return xnew
return secantMethods(f, xpresent, xnew, i=i+1)
print(secantMethods(f, 0.3, 0.4))6-5 수정할선법(Modified Secant Methods)
할선법과 동일하나, 2개의 초기값을 와 로 대치한 방법.
는 미소변동이다.
따라서, 두 초기값을 매우 좁은 간격으로 잡아서 접선처럼 구하도록 수정한 기법이다.
새로운 x좌표를 구하는 일반화 식
import numpy as np
def f(x):
return 7*np.sin(x)*np.exp(-x) - 1
# (d) modified secant method
def modifiedSecantMethod(f, x, delta, es=0.0001, i=1):
xnew = x - ((f(x) * (delta * x)) / (f(x + delta*x) - f(x)))
print("iter%d:"%(i), xnew)
ea = abs((xnew-x) / xnew)
if ea < es:
return xnew
return modifiedSecantMethod(f, xnew, delta, i=i+1)
print("Modified Secant Method")
print(modifiedSecantMethod(f, 0.3, 0.001))CHAPTER 7 최적화
어떤 것을 가장 효과적으로 만드는 과정이다.
이는, 최대/최소값 (극점) 찾기 → f'(x) = 0 인 점 찾는 것과 같다.
f'(x) = 0일 때, f''(x) > 0이면 최소값이고, f''(x) < 0 최대값이다.
7-1 1차원 최적화(One-dimensional Optimization)
단일 변수 함수 f(x)의 global optimum을 찾는 과정이다.
1) 황금 분할 탐색법(Golden-Section Search)
황금 비
을 만족하는 비.
황금비를 활용해 이분법과 비슷한 전략으로 최소값을 찾는 과정
-
최소값이 포함된 구간 설정.
-
새로운 중간값 2개를 계산
d = ( 이고,
x1 = x_l + d
x2 = x_u - d즉, 구간 사이에 각 점에서 61.8%가 떨어진 점을 새 중간값으로 계산한다.
-
이면, ,
이면, ,작은 쪽은 버리고, 큰 쪽만 살린다.
황금비를 사용하면, 위와 같이 구간을 좁혔을 때 나머지 중간값이 또 황금비를 만족하기 때문에 2개의 중간값을 구하는 것이 아닌, 1개만 구해도 된다.
-
*:x1, x2 중 함수값이 작은 값
import numpy as np
def f(x):
return (4*x) - (1.8*x**2) + (1.2*x**3) - (0.3 * x**4)
def goldenSectionSearch(f, xl, xu, es=0.0001, i=1):
phi = ((1+np.sqrt(5)) / 2)
d = (phi-1)* (xu-xl)
x1 = xl+d
x2 = xu-d
if f(x1) > f(x2): # max
xopt = x1
xl = x2
x2 = x1
d = (phi-1)* (xu-xl)
x1 = xl+d
else:
xopt = x2
xu = x1
x1 = x2
d = (phi-1)* (xu-xl)
x2 = xu-d
ea = (2-phi)*abs((xu-xl) / xopt)
print("iter %d:"%(i), xopt)
if ea < es:
return xopt
return goldenSectionSearch(f, xl, xu, i=i+1)
print("Golden-Section Search")
print(goldenSectionSearch(f, -2, 4))2) 2차 보간법 (Parabolic Interpolation)
점 세개가 있으면 이 세개를 지나는 포물선은 유일하게 결정할 수 있다. 포물선은 최대 최소값인 꼭짓점이 있다. 이러한 방식으로 최적화를 수행한다.
이 세 점을 지나는 2차 함수 식 f(x)을 유도하고, f'(x) = 0 으로 둬서 포물선의 최댓값을 구해 추정 최적값을 구한다. 이를 정리하면 다음 x4를 구하는 과정과 같다.
추정최적값
를 구한 후 나머지 과 비교해 최대값을 포함하는 x점 세 개를 선택해 이를 종료 조건까지 반복한다.
다시 점 세개를 결정하는 과정
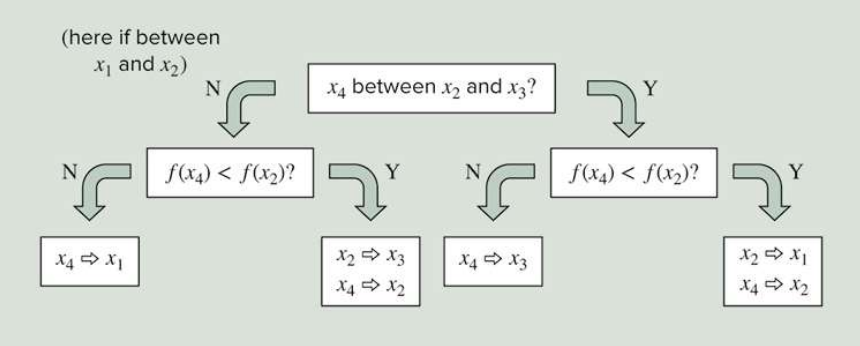
if abs(x2) < abs(x3) < abs(x4):
if f(x4) < f(x2):
x1 = x2
x2 = x4
else:
x3 = x4
else:
if f(x4) < f(x2):
x3 = x2
x2 = x4
else:
x1 = x43) Newton's Method
Newton-Raphson Method에서 g(x) = f'(x)를 두고 하는 것과 같다. Newton-Raphson Method는 근 구간법으로 근을 구하는 것이고, Newton's Method는 최적값을 구하는 것이다.
CHAPTER 8 선형대수방정식과 행렬 (Linear Algebraic Equations and Matrices)
import numpy as np
np.zeros([3, 4])
np.ones([4, 3])
np.eye(5, 5) # 대각행렬
A = np.matrix([[1, 1, 2],
[3, 5, 8],
[13, 21, 35]])
print(np.linalg.det(A))
print(np.linalg.norm(A))
print(np.linalg.inv(A))
print(np.linalg.matrix_rank(A))
print(np.trace(A)) # 대각선 element의 합
print(np.transpose(A))
b = [[1],
[2],
[3]]
x = np.linalg.solve(A, b)
print(x)CHAPTER 9 Gauss 소거법 (Gauss Elimination)
9-1. 순수 가우스 소거법(Naive Gauss Elimination)
import numpy as np
def gaussnaive(A, b):
n, m = A.shape
if n != m:
return 'Coefficient matrix A must be square'
# build augmented matrix (확장 행렬)
aug = np.hstack((A, b))
# # forward elimination
for i in range(n-1):
for j in range(i+1, n):
factor = aug[j][i] / aug[i][i]
aug[j] -= factor*aug[i]
# back substitution
x = np.zeros([n, 1])
x = np.matrix(x)
for i in range(n-1, -1, -1):
x[i] = (aug[i, n] - aug[i, i+1:n]*x[i+1:n, 0]) / aug[i, i]
return x
A = np.array([[3, -0.1, -0.2],
[0.1, 7, -0.3],
[0.3, -0.2, 10]])
b = np.array([[7.85],
[-19.3],
[71.4]])
x = gaussnaive(A, b)
print(x)9-2 Cramer 공식(Cramer's Rule)
n원 1차 대수 방정식에서 활용 가능.
3원 1차 대수 방정식이라고 하면, Ax = b 에서 다음과 같이 사용할 수 있다.
A1 = 1열을 b 행렬로 대체
A2 = 2열을 b 행렬로 대체
A3 = 3열을 b 행렬로 대체
ex.
이러한 방식으로 방정식을 풀 수 있다.
9-3 Pivoting
- 대각요소가 0이 되는 것을 방지하여 divided by zero를 방지
- 대각요소가 다른 계수보다 크도록 조정하여 해의 정확도 증가.
pivoting은 각 대각요소의 절대값이 가장 큰 값으로 행을 바꿔주는 것이다.
import numpy as np
def gaussPivot(A, b):
n, m = A.shape
if n != m:
return 'Coefficient matrix A must be square'
# build augmented matrix (확장 행렬)
aug = np.hstack((A, b))
# forward elimination
for i in range(n-1):
# partial pivoting
index = np.argmax(abs(aug[:, i])) # argmax: 절대값 최대인 요소 index 반환
aug[[i, index], :] = aug[[index, i], :]
for j in range(i+1, n):
factor = aug[j][i] / aug[i][i]
aug[j] -= factor*aug[i]
# back substitution
x = np.zeros([n, 1])
x = np.matrix(x)
for i in range(n-1, -1, -1):
x[i] = (aug[i, n] - aug[i, i+1:n]*x[i+1:n, 0]) / aug[i, i]
return x
A = np.array([[2, -6, -1],
[-3, -1, 7],
[-8, 1, -2]], np.float64)
b = np.array([[-38],
[-34],
[-20]], np.float64)
x = gaussPivot(A, b)
print(x)9-4 삼중대각 시스템(Tridiagonal Systems)
삼중대각 시스템은 주대각선을 중심으로 하는 띠의 폭이 3이며, 띠를 제외하고 모든 원소가 0인 정방행렬이다.
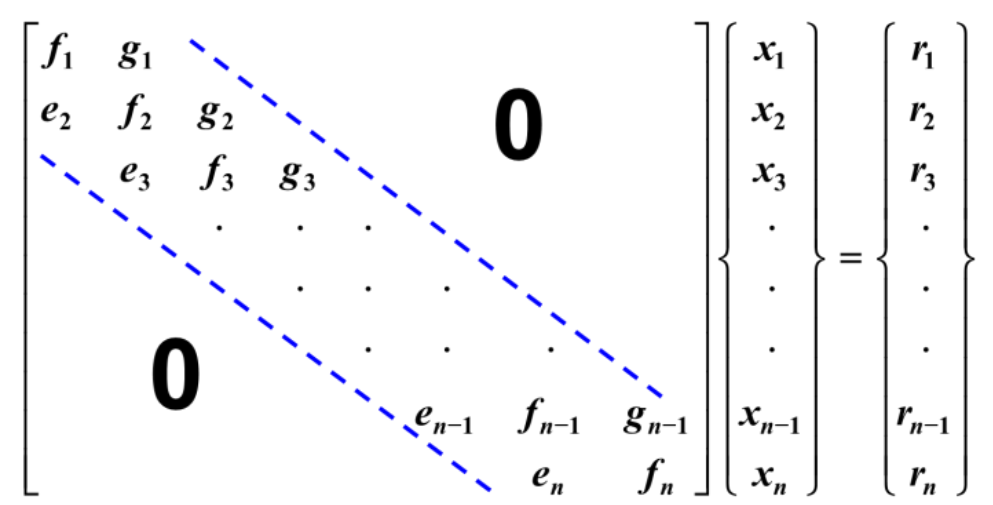
1) Thomas Algorithm
일반 Gauss 소거법과 같이 상삼각 형태로 형렬을 변형시켜서 푼다.
f1을 기준으로 e2를 기본행 연산을 통해 제거했을 때 g2는 영향을 받지 않는다. 이러한 방식으로 e들을 다 없애서 최종 해를 적은 연산으로 도출할 수 있다.
import numpy as np
def tridiag(e, f, g, r):
n = len(f)
# forward eliminaion
x = np.zeros([n])
for k in range(1, n):
factor = e[k] / f[k-1]
f[k] = f[k] - factor*g[k-1]
r[k] = r[k] - factor*r[k-1]
# back substitution
x[n-1] = r[n-1] / f[n-1]
for k in range(n-2, -1, -1):
x[k] = (r[k] - g[k]*x[k+1]) / f[k]
return x
e = np.array([0, -1, -1, -1], np.float64)
g = np.array([-1, -1, -1, 0], np.float64)
f = np.array([2.04, 2.04, 2.04, 2.04], np.float64)
r = np.array([40.8, 0.8, 0.8, 200.8], np.float64)
x = tridiag(e, f, g, r)
print(x)CHAPTER 10 LU 분해법 (LU Factorization)
10-1 LU 분해의 개념
A = LU 형태로 분해한다.
여기서, L은 하삼각행렬이면서 대각요소가 1인 행렬이고,
U는 상삼각행렬을 의미한다.
ex.
여기서 a, l, u는 각각 위치의 element를 뜻하며 같은 것이 아님. 편의를 위해서 저렇게 표기.
LU 분해를 하면 해를 쉽게 구할 수 있다.
Ax = b, A = LU라고 하면,
LUx = b
Ux = d
Ld = b
여기서, Ld = b식은 행사다리꼴과 유사하므로 대입해서 쉽게 d를 구할 수 있다.
그래서 d 행렬을 구하면, Ux = d도 행사다리꼴이기 때문에 그냥 대입해서 쉽게 구할 수 있다.
그러면, A를 LU 형태로 만드는 방법이 중요하다.
U는 A를 가우스 전진소거, 즉, 가우스 소거법으로 행사다리꼴로 만들면 된다.
L은 다음과 같은 방법으로 구할 수 있다.
A = LU =
즉, LU = A를 직접 행렬의 곱연산을 통해 방정식을 풀어서 구할 수 있다.
import numpy as np
import scipy as sc
import scipy.linalg
A = np.matrix([[3, -0.1, -0.2],
[0.1, 7, -0.3],
[0.3, -0.2, 10]])
b = np.matrix([[7.85],
[-19.3],
[71.4]])
P, L, U = sc.linalg.lu(A)
d = np.linalg.solve(L, b)
x = np.linalg.solve(U, d)
print(x)10-2 LU 분해를 이용한 행렬식 계산
- det(AB) = det(A) det(B)
- 삼각행렬의 행렬식은 대각원소의 곱과 같다.
따라서, A가 3차 정방행렬이라고 했을 때 A = LU로 분해되면
det(A) = det(L) det(U) =
즉, 상삼각행렬인 U의 행렬식과 같고, 이는 U의 대각원소의 곱과 같다.
10-3 Cholesky 분해법(Cholesky Factorization)
인 대칭행렬은 로 분해할 수 있다. 이를 Cholesky 분해법이라고 한다.
여기서 U는 상삼각행렬을 의미하며 다음과 같이 정의된다.
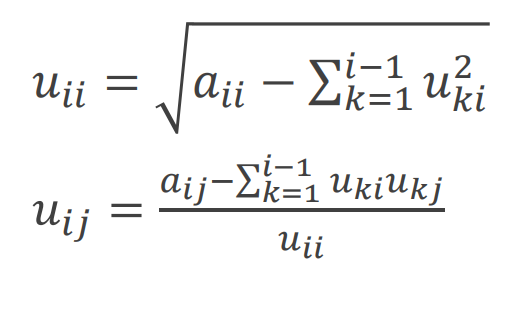
: 대각요소이고, 는 비대각요소이다.
import numpy as np
from scipy.linalg import cholesky
A = np.matrix([[6, 15, 55],
[15, 55, 225],
[55, 255, 979]])
U = cholesky(A)
print(U)CHAPTER 11 역행렬과 조건
11-1 LU 분해법 이용
Ax = b에서 A=LU로 분해하고, b에 을 차례로 대입한다.
Ax =
의 첫번째열
따라서, 3x3 인 경우
-
역행렬의 첫번째열
-
역행렬의 두번째열
-
역행렬의 세번째 열
이러한 형식이 된다.
11-2 불량조건
반올림오차에 의해 해가 심하게 변하는 문제
1) 불량조건의 징후
- 계수의 작은 변화로 해가 크게 변화되는 경우
- 행렬의 대각요소의 크기 < 비대각 요소 (대각요소 값이 x를 구할 때 분모값이 되고, 이 분모가 작으면 해가 크게 변할 수 있음. → pivoting을 써서 큰 대각요소를 사용하는 이유)
- 가 보다 I에 더 가깝지 않을 경우
2) 해결책
- pivoting을 실시하여 대각요소에 큰 값이 위치하도록 한다.
- 배정도(Double Precision)으로 정수 및 실수 표현시 메모리를 더 할당하게 하여 반올림 오차를 최소화 하도록 한다.
3) 불량조건의 판별
행렬의 조건수를 이용한다.
11-3 행렬 놈 norm과 조건수
norm: 벡터나 행렬과 같이 여러 개의 원소를 갖는 수학적 실체의 크기 또는 길이를 나타내는 척도
1) Euclidean Norm (Frobenius norm)
In Vector
In Matrix
즉, 각 요소를 제곱해서 더하고, 루트 씌운 것.
Euclidean Norm을 행렬에 사용하면 Frobenius norm으로 부른다.
2) P Norm
In Vector
- p = 2) Euclidean norm
- p = 1) 절대값의 합
- p = ) 절대값이 가장 큰 원소
In Matrix
- p = 1) : 열-합 norm, 각 열 요소의 절대값의 합 중 최대값
- p = 2) 의 최대 고유값
- p = : 행-합 norm, 각 행 요소의 절대값의 합 중 최대값
3) 행렬의 조건수 (Matrix Condition Number)
조건수가 클수록 시스템이 불량하다.
import numpy as np
A = np.matrix([[1., 1/2, 1/3],
[1., 2/3, 1/2],
[1., 3/4, 3/5]])
print("Forbenius norm =", np.linalg.norm(A))
print("cond no. =", np.linalg.cond(A))CHAPTER 12 반복법
12-1 선형방정식과 반복법(Linear Systems and Iterative Methods)
1) Gauss-Seidel Method
선형대수방정식을 푸는 반복법 중 가장 보편적인 방법.
새롭게 구한 x값을 새로운 x를 구할 때 반영시킨다.
Ax = b
Gauss-Seidel법의 특징
- (분모)
- n-1 개의 초기값 필요 (x1이면 이전 단계의 x2, x3가 필요하다.)
- 변수의 순차적 갱신
- 수렴 판별 조건
Gauss-Seidel법의 수렴과 대각지배
대각지배는 Gauss-Seidel 법이 수렴하기 위한 충분조건이다.
각 행에서 대각 계수의 절대값이 다른 계수 절대값의 합보다 커야한다.
대각지배를 만족하면 반드시 수렴하고, 만족하지 않아도 경우에 따라 수렴할 수 있다.
만약에 대각지배를 만족하지 않는 상태에서 수렴을 보장하고 싶다면 A 행렬의 행교환 연산을 통해 대각 계수의 절대값이 다른 계수의 절대값의 합보다 크게 만들어 대각지배를 만족시켜 수렴을 보장할 수 있다.
import numpy as np
def GaussSeidel(A, b, x, es=1e-07, iter=1):
n, m = np.shape(A)
if n != m:
return 'Coefficient matrix must be sqaure'
xold = np.copy(x)
maxEa = 0
for i in range(n):
x[i] = (b[i] - (np.dot(A[i], x) - (A[i, i] * x[i]))) / A[i, i]
ea = abs((x[i][0] - xold[i][0]) / x[i][0])
if maxEa < ea:
maxEa = ea
if maxEa < es:
return x
return GaussSeidel(A, b, x, es, iter+1)
A = np.matrix([[3, -0.1, -0.2],
[0.1, 7, -0.3],
[0.3, -0.2, 10]], np.float64)
b = np.matrix([[7.85],
[-19.3],
[71.4]], np.float64)
n, m = np.shape(A)
x = np.matrix(np.zeros((n, 1))) # 초기 x값을 각각 0으로 초기화.
x = GaussSeidel(A, b, x)
print(x)2) Jacobi Iteration
Gauss-Seidel Method와 전반적으로 비슷한 방법이나, 순차적으로 갱신해 나가는 것이 아닌 한번에 갱신하는 방법이다.
Ax = b
Jacobi Iteration의 특징
- (분모)
- n개의 초기값이 필요. (이전의 x1, x2, x3가 모두 있어야 현재의 x1, x2, x3를 구할 수 있다.)
- 변수의 동시적 갱신 → Gauss-Seidel 법보다 느린 수렴속도
3) 이완법 (Relaxation Method)
Gauss-Seidel 법에서 수렴을 위한 가감속을 부여하는 방법
의 구간 ()
- ) 에 대한 영향이 없어지므로 Gauss-Seidel 법과 동일함.
- ) 하 이완법(under-relaxation)
- 수렴이 잘 이루어지지 않을 때 사용할 수 있다.
- 해가 진동할 때 감쇠를 부여할 수 있다.
- ) 연속 상 이완법(Successive Over-Relaxation; SOR)
- 수렴이 잘되어서 수렴을 가속하고 싶을 때.
이완법의 적용
12-2 비선형방정식과 반복법(Nonlinear System adn Iterative Methods)
1) 연속대입법(Successive Substitution)
연속대입법 = 단순 고정점 반복법 + Gauss-Seidel method\
단순 고정점 반복법처럼 하나의 변수에 대해 정리하고 Gauss-Seidel 방법으로 이전 값을 통해 업데이트 한다.
method 1)
이 방법에서는 x1과 x2로 정리할 때 1차항을 가지고 정리했다.
첫번째 식은 x1에 대해 정리하고, 두번째 식은 x2에 대해 정리한다.
x1은 이전의 x1과 x2를 가지고 구하고, x2는 갱신된 x1과 이전 x2를 가지고 다음과 같이 구한다.
,
하지만, 이는 발산한다.
method 2)
이 방법에서는 x1과 x2로 정리할 때 2차항을 가지고 정리했다.
첫번째 식은 x1에 대해 정리하고, 두번째 식은 x2에 대해 정리한다.
x1은 이전의 x1과 x2를 가지고 구하고, x2는 갱신된 x1과 이전 x2를 가지고 다음과 같이 구한다.
,
이는 수렴한다.
연속대입법의 문제점
- 수식화를 어떻게 하느냐에 따라 수렴, 발산이 결정된다.
- 초기가정값이 해에 충분히 가까워야 한다.
2) Newton-Raphson 법
단일 변수 비선형 방정식
f(x) = 0 일때,
2원 비선형 방정식
f1(x1, x2) = 0, f2(x1, x2) = 0 일때,
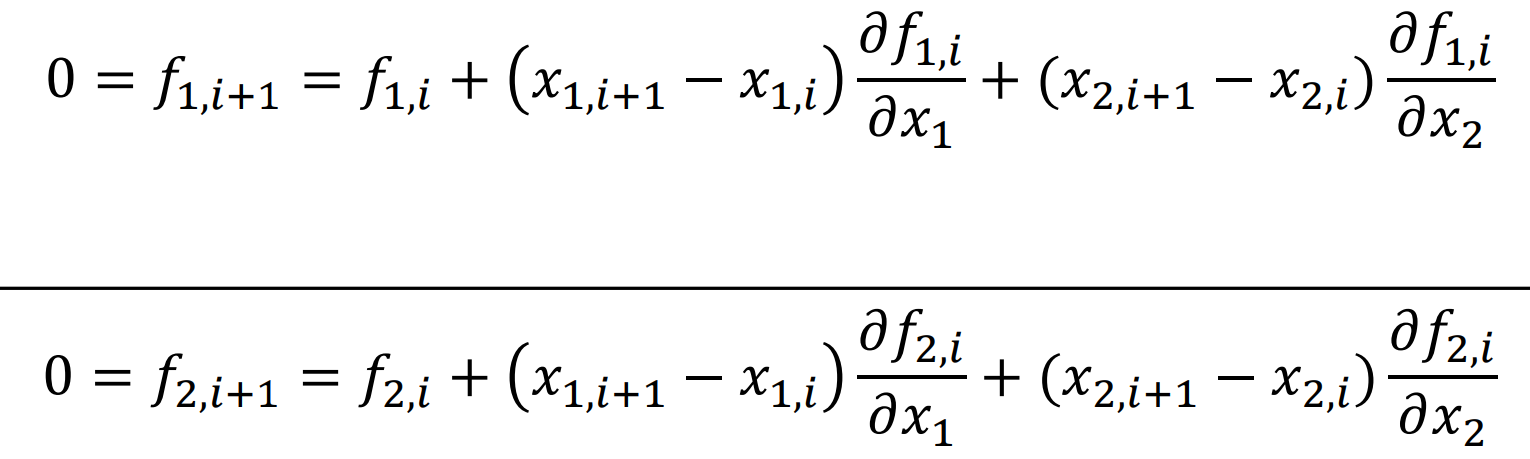

이 식에서 분모가 Jacobi 행렬식이다.
2원 비선형 방정식의 특징
- 2차 수렴(빠른 수렴)
- 초기 가정값이 해 근처여야 한다.
- 미분값을 구하기 어려울 경우 유한차분근사로 대체할 수 있다.
n원 비선형 방정식
f1(x1, ..., xn) = 0,
.
.
.
fn(x1, ..., xn) = 0
이를 행렬 F(X) = 0로 둔다.
Jacobian 행렬 J(X)
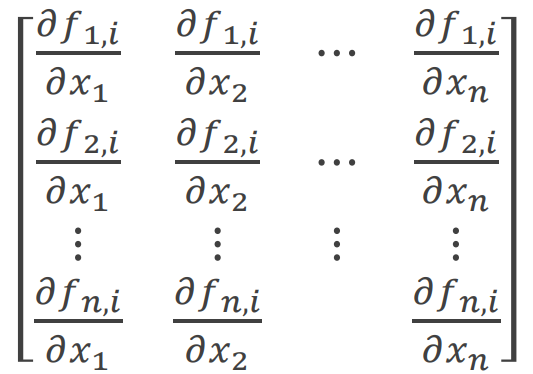
첫번째 행은 f1을 x1, x2, ..., xn으로 편미분
즉, n번째 행은 fn을 x1, x2, ..., xn으로 편미분하는 행렬이다.
를 구하기 않기 위해 라고 두면,
3) 최소화법(Minimization Method)
주어진 문제를 모아서 최소화된 문제로 변환하여 해를 구하는 방법.
n원 비선형 방정식
f1(x1, ..., xn) = 0,
.
.
.
fn(x1, ..., xn) = 0
이 있다면, 다음과 같이 조합할 수 있다.
h가 최소가 되는 것을 찾으면 최소화 문제가 된다.
h =0이면, f1=f2=...=fn = 0이다.
# Multivariable Root
import numpy as np
from scipy.optimize import root
def f(x):
f1 = x[0]**2 + x[0]*x[1] - 10
f2 = x[1] + 3*x[0]*x[1]**2 - 57
return np.array([f1, f2])
x0 = np.matrix([[1.5], # 초기 추정치
[3.5]])
result = root(f, x0)
xsoln = result.x
print(xsoln)