알고리즘 - 3. Search알고리즘

Ui Jin·2022년 4월 16일
알고리즘탐색 알고리즘
0

Algorithm

목록 보기
3/10

Search 알고리즘

우리는 앞에서 Sorting 알고리즘을 배웠다.
사실 이 Sorting을 하는 목적은 Search의 시간을 줄이기 위해서이다. Sorting이 되어 있는 경우 BinarySearch를 수행할 수 있기 때문에 시간을 많이 줄일 수 있기 때문이다.

  • Sorting이 되어있지 않을 경우
    : Search에 O(n)의 시간이 걸린다.
  • Sorting이 되어있을 경우
    : Search에 O(log(n))의 시간이 걸린다.

하지만 이마저도 데이터를 Sequential Data Structure에 저장할 경우 동적인 환경에서 사용할 때 삽입 시간이 오래걸릴 수 밖에 없다는 한계가 존재한다.

이를 해결하기 위해 다른 Data Structure를 활용하면 시간을 효율적으로 줄일 수 있게된다.
Data Structure의 종류에는 다음 3가지가 있다.

  1. Sequential Data Structure
  2. Hierarchical Data Structure
  3. Hash Data Structure

Hierachical Data Structure

먼저 Hierachical Data Structure, 그중에서도 Tree를 사용하는 방법을 살펴보자

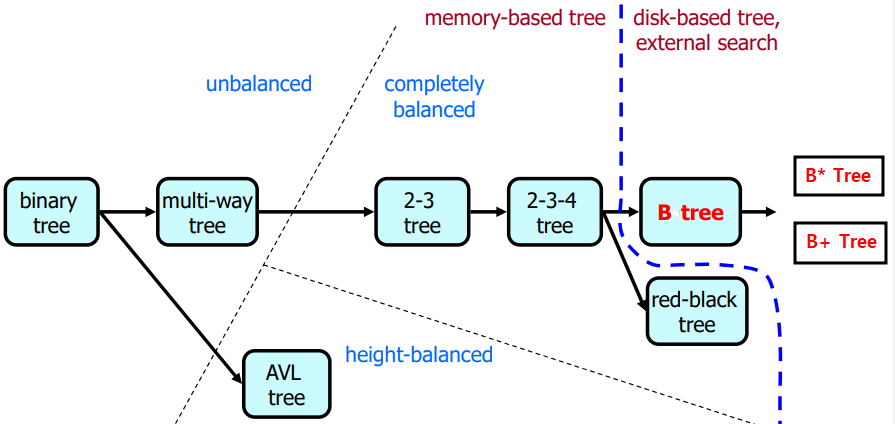
  • Sequential Data Structure
    • make: O(n log(n))
    • search: O(log n)
    • input: O(n log(n))
  • hierarchical data structure
    • make: O(n log(n))
    • search: O(log n)
    • input: O(log n)

(Sequential Data Structure의 input시간)

만약 ArrayVector일 경우 삽입할 때 자리를 찾고(O(log(n))) 그 자리에 대입(O(n))의 시간이 걸리기 때문에 총 O(n log(n))의 시간이 걸린다.

또, LinkedList일 경우에도 대입할 때는 시간이 걸리지 않지만, 자리를 찾는데에 총 O(n log(n))의 시간이 걸린다.

Unbalanced Tree

Unbalanced Tree는 Leaf Node들의 Level이 일정하지 않는 Tree구조를 말한다

1. Binary Tree

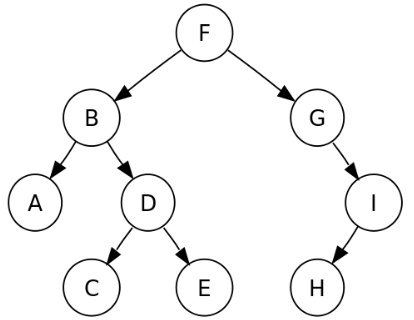
1) Binary Tree 조건

  1. Degree=2이다.

(중요한 Tree 용어)
1. Root Node: 부모가 없는 Node
2. Leaf Node: 자식이 없는 Node
3. Degree: Child Node의 최대 개수 (=Fanout, Order)
4. Depth: 해당 Node의 Ancestors의 수 (Node의 속성)
5. Height: Tree에 속한 Node의 Depth중 최댓값

2) Traversal

Tree를 탐색할 때, 방문 순서(코드처리 순서)를 결정하는 방법을 알아보자

Parent Node = P , LeftChild Node = L , RightChild Node = R

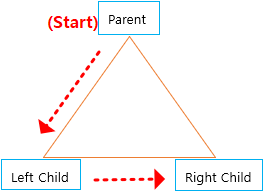
  1. PreOrder
    • 방문순서 (P-L-R)
    • Pseudo Code
    Preorder(v){
    visit(v);
    for each child w of v
        preorder(w);
}
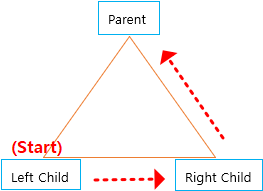
  1. PostOrder
    • 방문순서 (L-R-P)
    • Pseudo Code
    Postorder(v){
    for each child w of v
        Postorder(w);
    visit(v);
}
    • 사용 예시
      : 수식Tree를 PostOrder로 방문하면 후위 표기식으로 나타낼 수 있음.
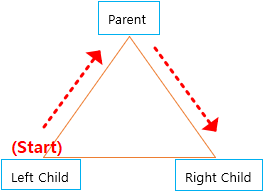
  1. InOrder
    • 방문순서 (L-P-R)
    • Pseudo Code
    Inorder(v){
    if isInternal(v)
        Inorder(leftchild(v));
    visit(v);
    if isInternal(v)
        Inorder(rightchild(v));
}
    • 사용 예시
      : 수식Tree를 Inorder로 방문하면 중위 표기식이 된다.

(참고: 위의 방문 순서는 Tree의 어떠한 SubTree를 골라 살펴보더라도 일치해야 한다. 이 방법으로 자신이 맞게 설정한 것인지 검토가 가능하다.)

2. Binary Search Tree

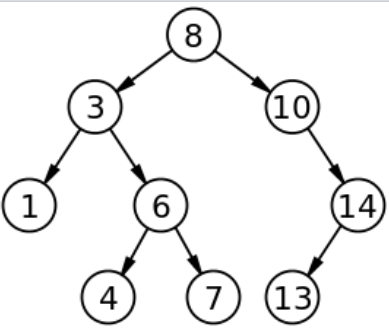
1) Binary Search Tree 조건

  1. degree=2이다
  2. 모든 SubTree에 대해 LeftChild <= Parent <= RightChild 이다.

(즉, Binary Tree의 한 종류이다.)
(2번 조건을 활용해 BST가 맞는지 검토할 수 있다.)

2) 주요특징

  1. BST를 Inorder Traversal로 노드를 방문할 경우 오름차순 정렬이 된다.
    • 이 때, i번째 방문한 값에 대해
      • i-1번째 방문한 값은 Predecessor이다.
      • i+1번째 방문한 값은 Successor이다.
  1. Root에서 LeftChild로 이동을 반복하면 Min값이 나오고,
    Root에서 RightChild로 이동을 반복하면 Max값이 나온다.
  1. Predecessor에는 해당 Node보다 바로 작은 값이 있고,
    Successor에는 해당 Node보다 바로 큰 값이 있다.

(참고)
Predecessor: 해당 Node에서 Left Child로 한번 이동 후 계속 Right Child로 이동하면 나온다.
Successor: 해당 Node에서 Right Child로 한번 이동 후 계속 Left Child로 이동하면 나온다.

원하는 값이 나올 때 까지 찾을때 까지 Binary Search Tree의 2번조건을 활용해 Right Child와 Left Child로 옮겨가며 찾는다.

(이 때 존재하지 않는 원소일 경우 해당 원소가 들어가야 할 Leaf Node를 반환한다.)

4) Insertion

A(어떤 값)를 Insertion한다고 하자.

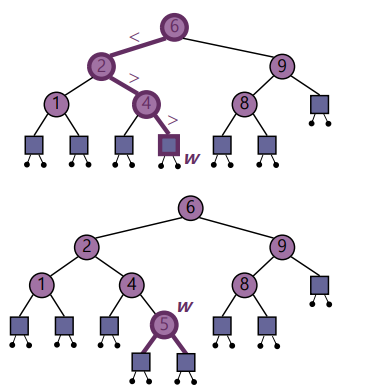
  1. 먼저 BST에서 A를 Search한다.
    : 찾은 Node가 Internal Node일 경우 Right Child(혹은 Left Child)로 자리를 옮긴 후 다시 Search를 수행한다.
    : 찾은 Node가 External Node일 경우 찾기완료
  1. 찾은 노드에서 RightChild(혹은 LeftChild)를 새로 만들고 대입한다.

5) Deletion

A(어떤 값)를 Deleteion한다고 하자

External Node일 경우

  1. 바로 삭제한다.

Internal Node일 경우

  1. A의 Successor 또는 Predecessor인 B 찾는다.
    : B가 Internal Node일 경우 RightChild(혹은 LeftChild)로 자리를 옮긴 후 다시 찾는다.
    : B가 External Node일 경우 찾기완료
  1. B와 A의 위치를 바꾼다.
    : 여기서 A는 External Node로 바뀐다
  1. External Node가 된 A를 삭제한다

bit의 특징을 활용해 Tree에 저장하고 search

Insertion

  1. Key의 값을 2진법으로 구현
  1. MSB부터 LSB부터 차례대로 1이면 오른쪽, 0이면 왼쪽으로 이동하며 Leaf Node를 찾는다.
  1. 찾은 자리에 저장한다.

Search

  1. MSB부터 LSB부터 차례대로 1이면 오른쪽, 0이면 왼쪽으로 이동하며 Search Key와 비교한다.

(계속 비교해야 하는 이유: Insertion시 중간에 Leaf Node가 나올 때 Insertion을 수행했기 때문이다.)
(즉, Search Key의 크기가 큰 경우 비교횟수가 늘어나므로 탐색 시간이 늘어난다.)

2) Radix Search Trie

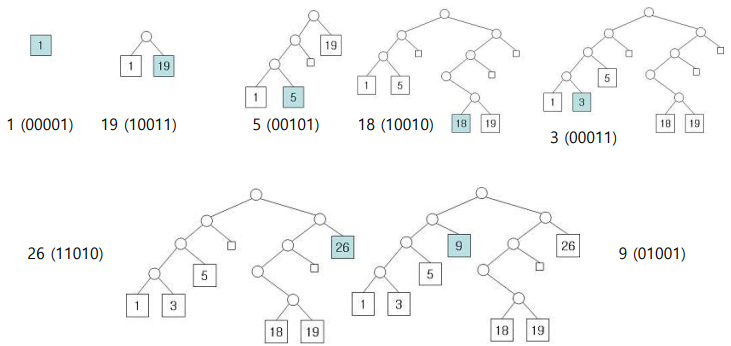
Insertion

  1. Radix Search와 같다

(단, 값을 저장하는 자리는 무조건 Leaf Node이다.)

Search

  1. Radix Search와 같지만 Leaf Node에 도착하기 전에는 비교를 하지 않아도 된다.

장점
: Key 비교를 덜하기 때문에 Search에 더 적은 시간이 걸린다

단점
: Internal Node에는 저장하지 않기 때문에 저장 공간의 낭비가 많다.-
: 프로그래밍이 더 어렵다.

3) Patricia

Binary Tree의 형태를 띄지만 상향링크가 있다는 특징이 있다.

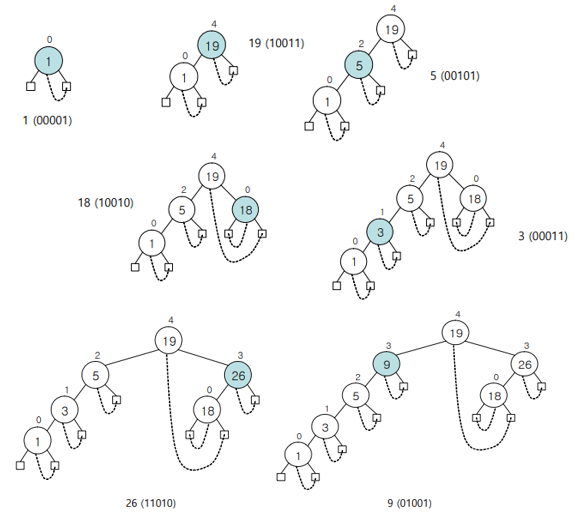
Radix Search의 비교횟수가 많다는 단점과
Radix Search Trie의 저장공간 낭비가 심하다는 단점을 해결하기 위해 만들어진 알고리즘이다.

Insertion
1. Internal Node에도 Key를 저장한다.

Search
1. 상향링크를 만날 때에만 키 비교를 수행한다.

Balanced Tree

Balanced Tree는 모든 Leaf Node들이 항상 같은 Level에 있는 Tree를 의미한다.
이 Balanced 속성을 지키기 위해서 Insertion할 때 Overflow Handling이 필요하고 Deletion할 때는 Underflow Handling이 필요하다..

1. 2-3Tree & 2-3-4Tree

1) 2-3(-4)Tree 조건

2-3 Tree의 경우

  1. Balanced Tree이다
  2. Degree=2 또는 Degree=3 이다.
    (즉 한개의 Node가 가지는 Element수는 1또는 2이다)
  3. 모든 SubTree에 대해 LeftChild <= Parent <= RightChild 이다.

2-3-4 Tree의 경우

  1. Balanced Tree이다
  2. Degree=2 또는 Degree=3 또는 Degree=4 이다.
    (즉 한개의 Node가 가지는 Element수는 1또는 2또는 3이다)
  3. 모든 SubTree에 대해 LeftChild <= Parent <= RightChild 이다.

원하는 값이 나올 때 까지 찾을때 까지 3번조건을 활용해 Right Child와 Left Child로 옮겨가며 찾는다.

3) Insertion

Overflow란?
2-3 Tree와 2-3-4 Tree는 각각 한개의 Node에 들어갈 수 있는 원소의 수가 정해져있다. 하지만 아래와 같이 원소를 Insertion할 때 정해진 값보다 많이 들어가게 될 때가 있는데 이것을 Overflow라고 한다.

  1. 먼저 Insertion을 수행할 Node를 찾는다.
  1. Overflow가 발생하지 않을 경우
    : 해당 Node에 그냥 대입한다.
  1. Overflow가 발생할 경우
    : Overflow Handling을 수행한다.

Overflow Handling?
: Overflow가 발생할 경우 해당 Node를 Split하여 균형을 유지하도록 하는 방법을 의미한다.
(Overflow Handling을 할 때 Root까지 Propate 될 수 있으니 주의하자.)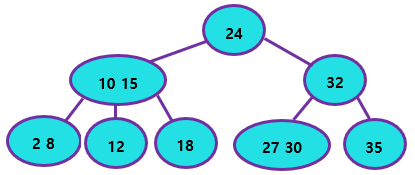

(위 그림의 Overflow Handling 결과)

  1. Node안에서 중간값을 고른다.
  1. 해당 값을 Parent Node로 올린다.
  1. Parent Node를 기준으로 Child Node를 다시 Split한다.
  1. Overflow가 Parent Node로 Propagate되었을 경우 Parent Node에 대해 2~3과정을 다시 수행한다.

4) Deletion

Underflow란?
2-3 Tree와 2-3-4 Tree에서 각각의 Node는 반드시 한개 이상의 원소를 가져야 한다. 하지만 만약 1개의 원소를 가진 Node에서 Deletion을 수행해야 한다면, Node의 Element가 없어질 것이다. 이것을 Underflow라고 한다.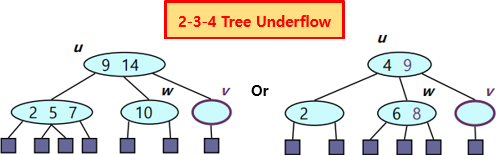

  1. 먼저 Deletion을 수행할 Node를 찾는다.
  1. Underflow가 발생하지 않을 경우
    • Leaf Node일 경우
      : 바로 삭제를 수행한다.
    • Leaf Node가 아닐 경우 (BST랑 같다.)
      : Leaf Node에 있는 Predecessor 또는 Successor를 골라 자리를 바꾼다.
      : 그 후, 삭제를 수행한다.
  1. Underflow가 발생할 경우
    : Underflow Handling을 수행한다.

Underflow Handling?
: Underflow가 발생할 경우 두 Node를 Merge하여 균형을 유지하도록 하는 방법을 의미한다.
(Underflow Handling할 때 Root까지 계속 Propagate될 수 있으니 주의하자)

Case1: Adjacent Sibling의 element가 1개인 경우

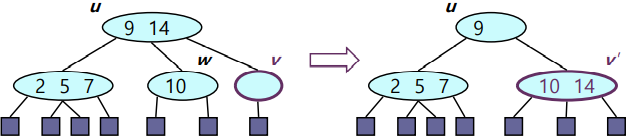
  1. 비어버린 Node와 Sibling의 Node를 합친다.
  1. 1번과정을 통해 한쪽 Child가 없어진 Parent Node를 밑으로 내린다.
  1. 1~2번 과정을 마친 후 Parent Node로 Underflow가 Propagate 되었을 경우 다시 case를 파악 후 Underflow Handling을 수행한다.

Case2: Adjacent Sibling의 element가 2개 이상인 경우

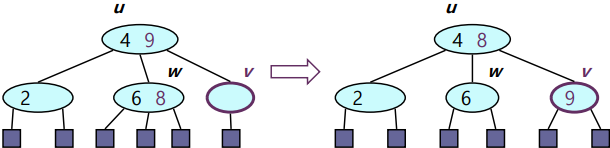
  1. Parent의 Element를 내려 비어버린 Node를 채워준다.
  1. Silbing의 Element를 올려 공석이 된 Parent를 채워준다.
    : 이 경우 Underflow가 발생하지는 않는다.

5) 참고사항

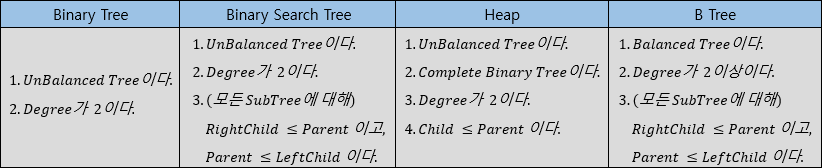
  1. 몇몇 Binary Tree의 특징 비교

(참고: B Tree에 2-3Tree, 2-3-4Tree도 포함된다.)

  1. 풀어볼 만한 문제

2. Red Black Tree

2-3-4 Tree를 표현만 Binary Tree형태로 바꾼 것
(즉, 하나의 Node에는 하나의 Element가 존재한다.)

3. B-Tree & B*Tree & B+Tree

Disk-Based Tree이고 Degree의 수가 더 많다는 것을 제외하면 2-3-4Tree와 거의 비슷하게 동작한다.

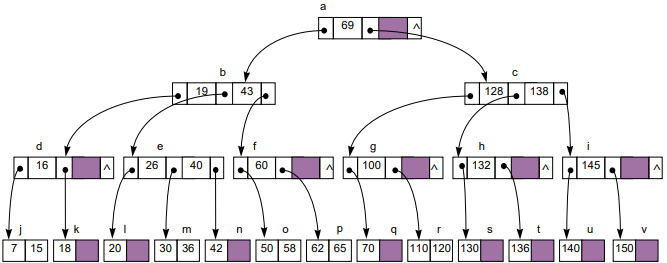
1) 조건

  1. Disk-Based Tree이다.
  2. Balanced Tree이다
  3. Degree는 2 이상의 원하는 설정값을 가진다.
    (보통 Disk의 1Page수(50~100)로 설정하면 성능이 좋다고 한다.)
  4. 모든 SubTree에 대해 LeftChild <= Parent <= RightChild 이다.

기존의 Tree 자료구조들은 메모리에 올려 사용했지만, BTree는 Memory가 아닌 Disk에 구현한 자료구조이다.

(Memory-Base: new, delete와 같은 연산들을 사용하는 자료구조)
(Disk-Base: seek, open, read, write와 같은 연산들 사용하는 자료구조)

2) Insertion과 Deletion

다음의 Overflow, Underflow조건을 제외하면 2-3-4Tree와 완전히 동일하게 동작한다.

  1. B-Tree
    • Overflow 조건: Node의 element수가 설정한 값보다 커질 때
    • Underflow 조건: Node의 element수가 설정한 값/2 -1 보다 작아질 때
  1. B*Tree
    • Overflow 조건: Node의 element수가 설정한 값보다 커질 때
    • Underflow 조건: Node의 element수가 설정한값*2/3보다 작아질 때

(참고)
: Underflow의 조건을 좀 더 크게하여 낭비되는 공간을 줄이려고 시도했지만 Underflow가 많이일어나면서 의도와는 다르게 동작시간이 늘어나 실패하였다.

3) B+ Tree

B+Tree는 B-Tree에서 다음과 같이 몇가지 특징이 변형된 자료구조이다

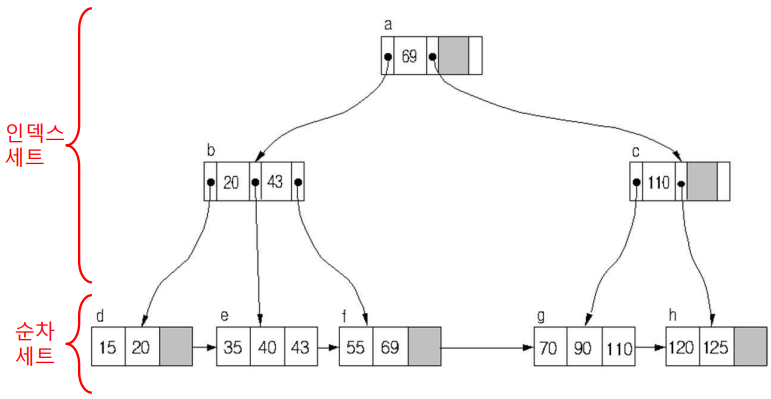
  1. Leaf Node (순차세트 표현)
    : B-Tree에서 모든 Value들을 Leaf Node에 표기한다.
    • 이때, 모든 Leaf Node들은 연결한다.
  1. Internal Node (인덱스세트 표현)
    : Child Node를 Root로 하는 SubTree의 최대값을 보관한다.
    • 즉, LeafNode와 중복되는 값이 항상 저장된다.
  1. 장점
    : 순차세트와 인덱스 세트를 나누었다는 것과 Leaf Node들이 연결되어 있다는 특징 때문에 Range탐색이 가능하다.
  1. 단점
    : 중복된 값이 항상 저장되기 때문에 저장공간이 많이 필요하다.
    : 모든 값은 LeafNode에 있기 때문에 탐색 시간은 항상 O(log(n))이 필요하다.
    (B-Tree보다 동작 시간이 오래 걸린다.)

(Search의 종류: Target Search, Range Search)
Range 탐색이 가능하다는 장점 때문에 실제 DB같은 곳에서는 B-Tree가 아닌 B+Tree가 사용된다.

Hash Data Structure

배열과 더불어 Hash function을 가지는 데이터구조이다. 이 Hash function을 통해 Hash Table을 만든다는 특징이 있다.

1. Hash Table

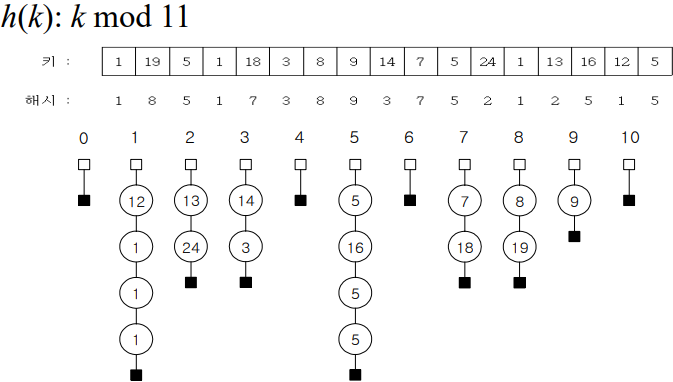
1) Hash Table의 Insertion

Hash Function을 활용해 저장한다.

저장 과정

  1. 추가적인 저장공간인 Bucket(배열)을 만든다.
    : 이 때 Bucket의 크기는 데이터의 수보다 크거나 같아야 한다.
  1. 넣고자 하는 객체(id, 이름)를 우선 숫자로 만든다.
  1. 해당 숫자를 Hash Function을 통해 특정 범위내의 수로 압축한다.
  1. <클러스터링 방지 대책 수행>
  1. Bucket(배열)의 index(위의 결과로 얻은 수)에 저장한다.

(참고: 클러스터링 방지 대책을 설정해주지 않을경우 중복된 값이 발생하면 index+1에 저장한다.)

클러스터링

  1. 클러스터링이란?
    : 데이터들의 Hash function을 거친 값들이 중복되는 경우가 많은 경우를 의미한다. (이 경우 탐색시간이 늘어난다.)
  1. 클러스터링 방지대책
    • 1) Double Hashing
      : Hash function을 두개 만들어 클러스터링이 발생할 경우 사용하는 방법이다. 중복된 값이 있을 경우, 두번째 Hash function의 결과값을 더해서 index를 얻게된다.
    • 2) Bucket doubling
      : Bucket이 데이터에 비해 너무 작을 경우 충돌이 많이 발생하게 된다. 이를 막기위해 Bucket의 크기를 키워준다.

(예시)

...

Hash function을 활용하여 찾으면 되기 때문에 평균적으로 5번 이하의 탐사 횟수를 가진다.

장점
: Target Search에 대해 O(1)의 매우 빠른 속도를 가짐

단점
: Range Search가 불가능하다.
: 최악의 경우 충돌이 많이 발생해 탐색시간이 O(n)까지 커질수 있다

위의 단점을 보완하고 장점을 최대한 활용하기 위해 실제 DB에서는 Hash Table과 B+Tree모두 사용한다

  • 트리들 특징
  • BST deletion
  • 2,4 Tree insertion, deleteion
  • Btree, Btree와 B+tree의 차이
profile
Ui Jin
github로 이전 중... (https://uijinee.github.io/)
이전 포스트

알고리즘 - 2. 정렬알고리즘

다음 포스트

알고리즘 - 4. String 탐색

0개의 댓글