베이즈 통계학

1. 조건부 확률

1) 정의

어떤 사건 A가 이미 일어났을 때 다른 사건 B가 발생할 확률을 의미한다.

---

• 확률P(B): 모든 경우의 사건 중에서 사건 B가 일어날 확률
• 조건부 확률P(B|A): 사건 A 중에서 사건 B가 일어날 확률

2) 공식

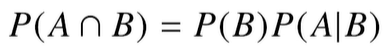
• P(AnB)는 A와 B가 동시에 일어날 확률
  (P(A, B)라고도 함)

• P(A|B)는 B가 이미 일어났을 때, A가 일어날 확률

3) 의미

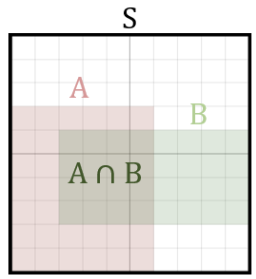
위의 그림을 잘 살펴보자.

---

1. 일반적인 확률의 의미

• 아직 아무런 사건도 일어나지 않았다.
• 즉, 사건 S가 일어날 수 있는 모든 경우의 수가 된다.
• P(S) = 1이다.

---

2. 조건부 확률의 의미

• A는 이미 일어난 사건이다.
• 즉, 사건 A가 일어날 수 있는 모든 경우의 수가 된다.
• P(A) = 1이다.

---

3. 주의점

• 이 조건부 확률을 통계적 해석이 아닌 인과관계 추론에 활용하고자 할 때에는 각별한 주의가 필요하다.

2. 베이즈 정리

1) 정의

조건부 확률을 활용하여 미래의 사건에 대해 확률을 예측하는 방법

2) 공식

• 사전확률: 단순히 사건 Theta가 발생할 확률
• 사후확률: 과거의 정보들을 취합해 이를 활용하여 사건 Theta가 일어날 확률

---

데이터의 Update

: 데이터가 새롭게 갱신되었을 때, 이전에 알고 있던 사후 확률을 사전 확률로 사용하면 갱신된 사후 확률을 쉽게 계산할 수 있다.

3) 의미

• 과거에 관측했던 사건의 정보들을 활용해 미래의 사건을 예측할 수 있다.
• 수학적으로 증명된 방식으로 미래를 예측할 수 있다.

---

단, 모든 경우에 대한 사건의 확률을 알고 있어야 한다는 단점이 있다.