여태까지는 Query를 사용하는 방법에 대해서 배웠었다면,
여기서는 Data Base가 Query를 내부적으로 어떻게 수행하는지에 대해서 공부해볼 예정이다.
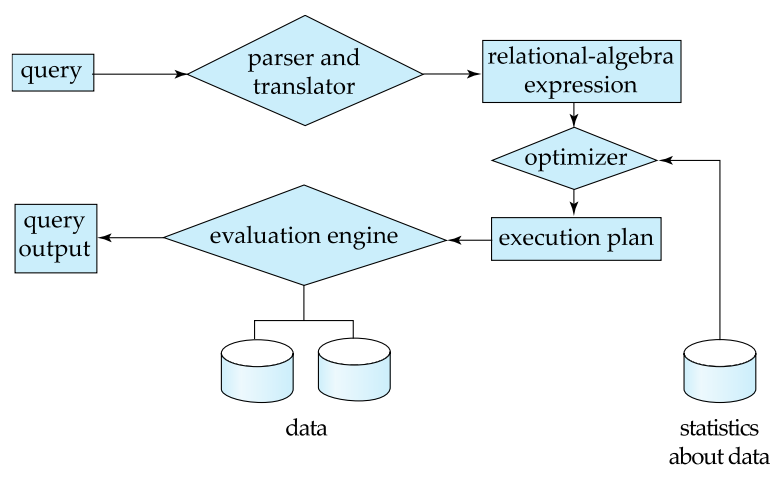
먼저 우리가 Query를 입력하면 컴퓨터 내부적으로 위와 같은 작업들이 실행된다.
요약해보자면
- 해당 SQL Query를 Relational Algebra로 바꾼다.
- Optimizer를 통해 어떤 방법으로 해당 Query를 수행하면 좋을 지 결정한다.
- 위에서 결정한대로 Plan을 세우고 실행하여 결과를 얻는다.
와 같은 과정을 거친다.
이 때, Optimizer는 통계적 데이터를 사용하는데,
예를들어 데이터의 분포범위나, 평균 같은 것들을 활용하게된다.
앞에서 공부했던 내용과 마찬가지로 I/O Complexity를 줄이는 방향으로 Query수행 계획을 세워야 한다.
이 때, 우리가 사용할 Main Memory의 Buffer의 크기는 매우 작다고 가정해야한다.
(참고: 앞에서 사용했던 용어들을 다시한번 복습해보자)
B: 하나의 Block에 들어갈 수 있는 Record의 최대 개수
M: Memory의 Buffer에 들어갈 수 있는 Record의 최대 개수
N: Input Data의 Record의 개수
Selection
다음은 우리가 원하는 Data들을 뽑아오는 과정,즉 Select문을 어떻게 구현할 수 있는가에 대한 방법들이다.
이 방법에는 Data File자체를 탐색하는 방법과 Index File을 활용해 탐색하는 방법이 존재한다.
1. File Scan
다음은 Data File자체를 탐색하는 방법이다.
1) A1 알고리즘

1. 정의
Data File 자체를 Scan하는 알고리즘으로 그냥 모든 block을 한번씩 읽어 원하는 record를 찾는 방법. Linear Search라고도 한다.
2. 사용가능 상황
어떠한 상황에도 사용 가능하다.
3. I/O Complexity
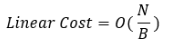
2. Index Scan
다음은 Index File을 활용해 데이터를 찾는 방법들이다.
1) A2 알고리즘
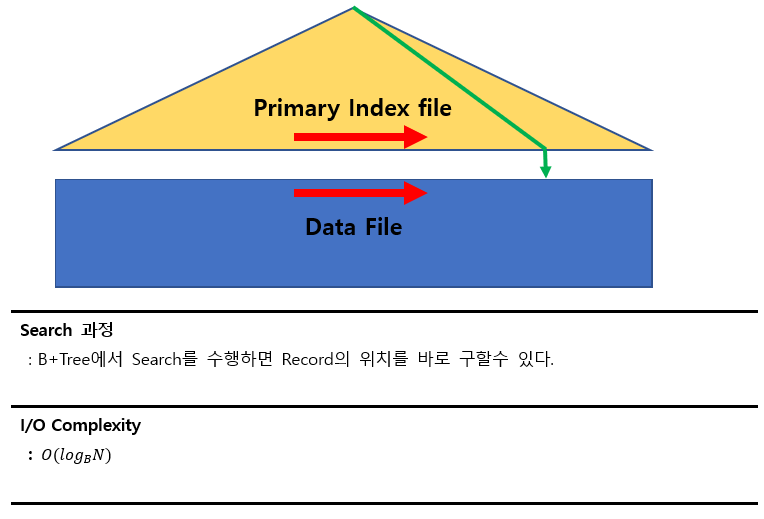
Index File의 조건
- Primary Index File
- B+Tree Index File
즉, 데이터 파일의 순서와 index파일의 순서가 같아야 한다.
검색조건
- Equality on Key
(Relation에서 Key를 찾는 알고리즘이므로 Single Record를 찾는다.)
I/O Complexity는 B+ Tree의 높이가 될 것이다.
2) A3 알고리즘
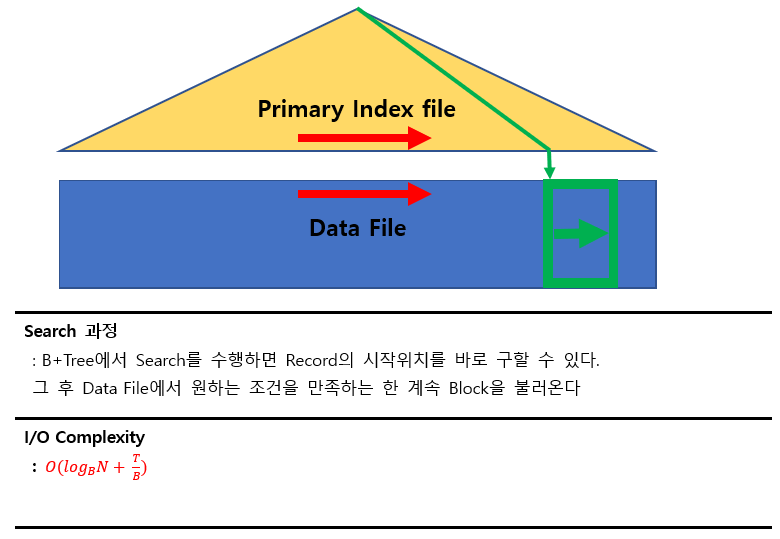
Index File의 조건
- Primary Index File
- B+Tree Index File
즉, 데이터 파일의 순서와 index파일의 순서가 같아야 한다.
검색조건
- Equality on Non-key
(Relation에서 Key가 아닌 Attribute를 찾는 알고리즘이므로 Multiple Record를 찾아야 한다.)
(Output의 개수에 따라 I/O Complexity가 달라진다. 이것을 Output Sensitive라고도 한다.)
3) A4 알고리즘
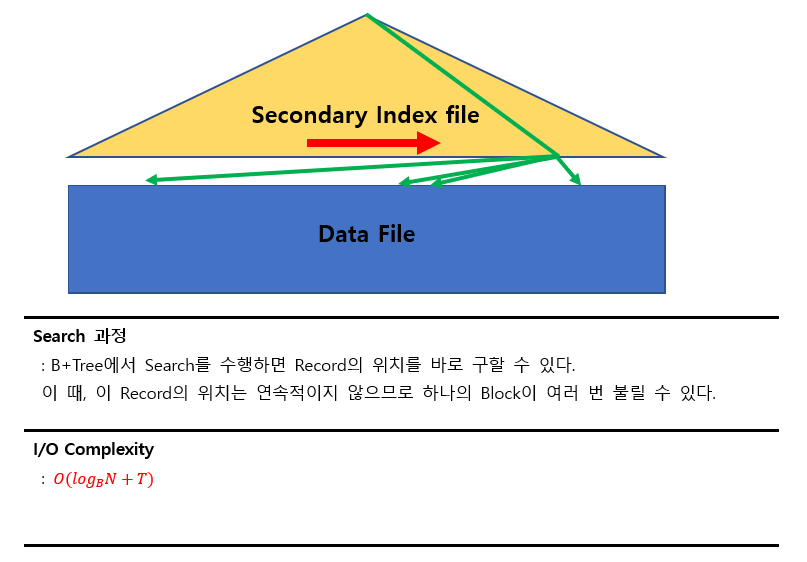
Index File의 조건
- Secondary Index File
- B+Tree Index File
즉, 데이터 파일의 순서와 index파일의 순서가 다르다.
검색조건
- Equality on Non-key
(Relation에서 Key가 아닌 Attribute를 찾는 알고리즘이므로 Multiple Record를 찾아야 한다.)
이 경우 T의 크기에 따라 File Scan을 사용하는 것이 더 나은 방법이 될 수 있다.
만약 같은 조건에서 검색조건이 Key로 바뀐다면 A2와 같이 동작하고
O(log_B(N))의 I/O Complexity를 가질 것이다.
4) A5 알고리즘
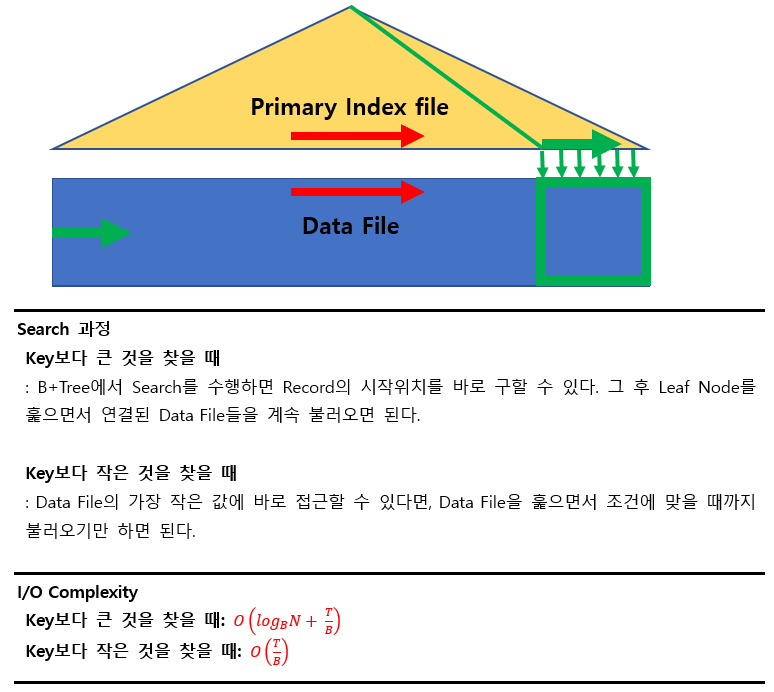
Index File의 조건
- Primary Index File
- B+Tree Index File
즉, 데이터 파일의 순서와 index파일의 순서가 같아야 한다.
검색조건
- Range Search
(어차피 여러개의 Block을 불러와야 하므로 I/O Complexity의 관점에서 Key의 여부와는 크게 상관없다.)
Data File이 Singly하게 연결되어 있다는 것을 가정할 때, Key보다 작은 값을 찾을 때에는 뒤로 가는 것을 할 수 없다.
5) A6 알고리즘
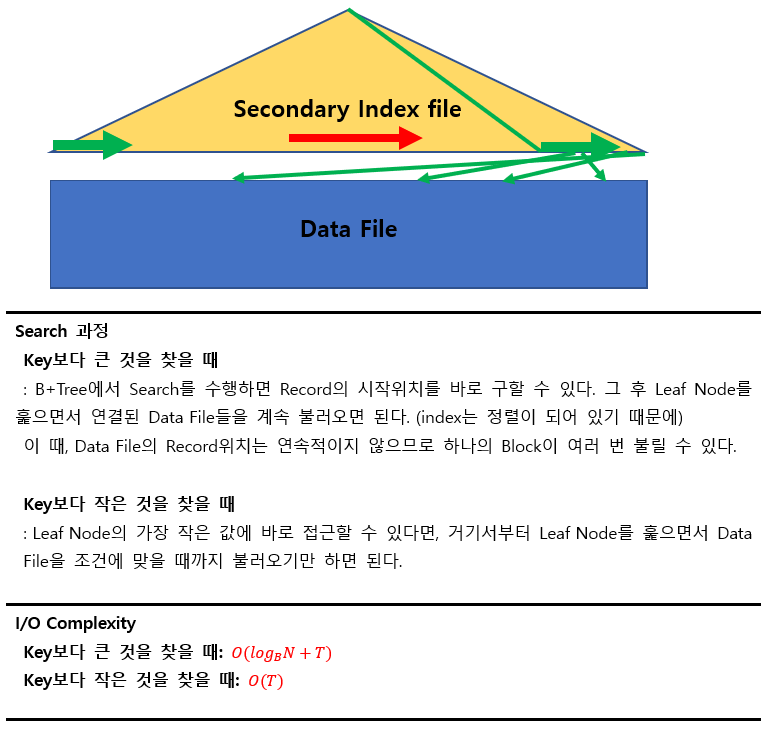
Index File의 조건
- Secondary Index File
- B+Tree Index File
즉, 데이터 파일의 순서와 index파일의 순서가 다르다.
검색조건
- Range Search
(어차피 여러개의 Block을 불러와야 하므로 I/O Complexity의 관점에서 Key의 여부와는 크게 상관없다.)
이 경우 T의 크기에 따라 File(Linear) Scan을 사용하는 것이 더 나은 방법이 될 수 있다.
Sorting
Secondary index의 경우 Index를 활용하여 Sort를 할 때, Block을 데이터의 개수만큼 불러와야 하기 때문에 Linear한 방법보다 오히려 나쁜 효율을 가진다.
따라서 별도의 Sorting 알고리즘이 필요하다.
또 이 Sorting알고리즘의 복잡도를 계산할 때 B < M << N을 가정하고 분석할 것이다.
1. External Mergesort
1) 정의
Input
: N개의 Record로 구성된 매우 큰 FileMemory
: Memory에 들어갈 수 있는 최대 Record의 수Run
: 정렬된 Output File.
2) 동작 과정
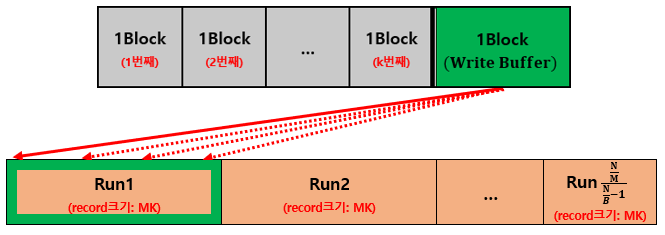
- 전체 Data에서 M개씩 Record를 읽어 Memory에서 Sort하여 Run을 만들고, 이를 External Memory에 다시 Write한다.
- Run의 크기
:M- Run의 개수
:N/M- I/O Complexity
:O(N/B)
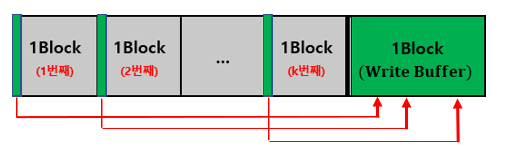
- 앞에서 부터 K개의 Run을 선택해 각 Run의 가장 앞부분의 1Block을 Memory로 가져온다.
- 이때, 1개의 Block은 Write Buffer로 비워둔다.
- 각 Block에서 맨 앞을 비교해 가장 작은 값들을 WriteBuffer에 이동시키는 작업을 WriteBuffer가 가득찰 때 까지 반복한다.
- 이때, Block이 빌 경우 연결된 Run에서 1Block을 다시 가져온다.
(각 Block은 Run에서 온 것이므로 이미 정렬되어 있다.)
- 가득 찬 WriteBuffer를 다시 External Memory로 옮겨준다.
- 3~4번 작업을 Memory에 연결된 Run의 데이터가 모두 사라질 때까지 반복한다. (1개의 Run 완성)
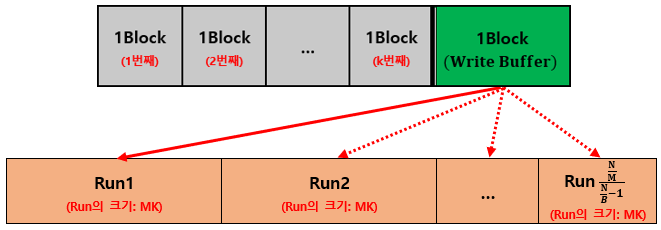
- Run의 크기
:MK- Run의 개수
:(N/M)/K- I/O Complexity
Read:O(K*M/B)
Write:O(K*M/B)(
M/B개의 Run들을 K개 만큼 가져왔고 이는 Write에도 적용되기 때문이다.)
- 2~5번 작업을 External Memory의 모든 Run의 데이터가 사라질 때까지 반복한다.
3) 동작과정 분석
1. Memory의 크기가 충분한 경우

2. Memory의 크기가 충분하지 않은 경우

(Memory의 1Block을 남겨놓아야 하므로 K의 최대값은
(M/B)-1이어야 한다.)
Join
DB에서 가장 중요한 연산임
r과 s를 join할 때,
Nr은 r Table의 Record
Ns는 s Table의 Record
B는 일단 같다고 가정
(실제는 각 Relation에서 Tuple의 Size가 다르므로, 둘의 사이즈는 다르다.)
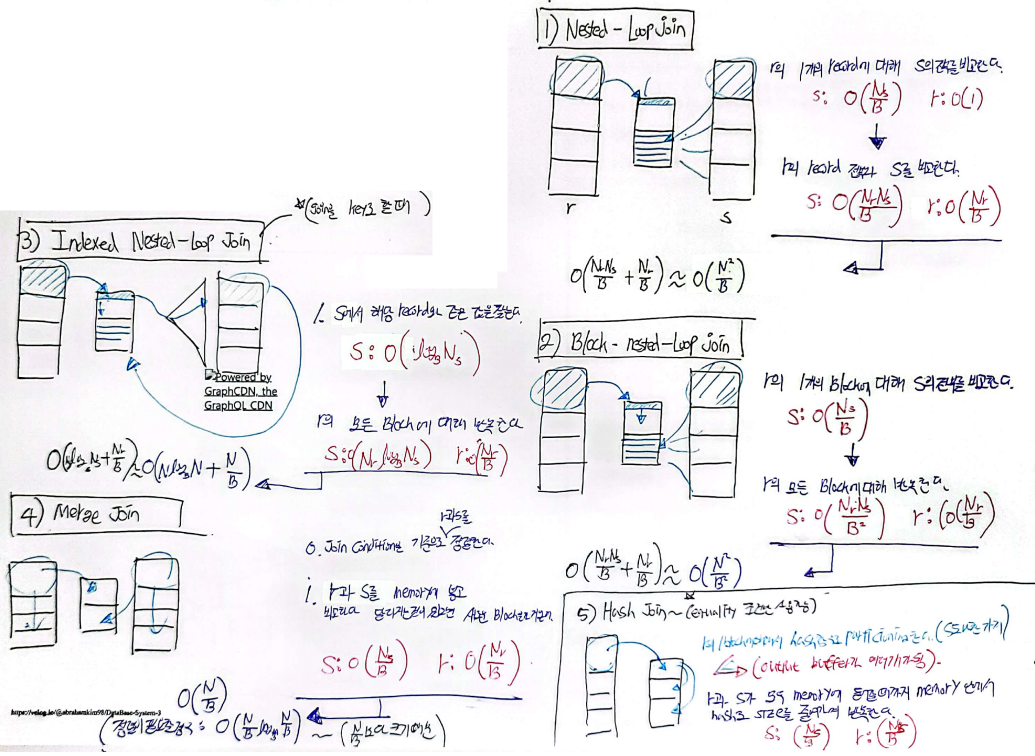
1) Nested-loop Join
r은 Memory에 유지 MRU전략으로 s를 Memory에서 계속 바꿔줌
O(Nr*Ns/B)
2) Blok nested-loop Join
r과 s를 메모리에 올린 후 일단 모든 record를 비교하고 바꾸는 방법
O(Nr/B*Ns/B + Nr/B)
3) Indexed nexted-loop Join
S가 B+ Tree 의 Primary Index일 때,
Equality on key of s일 때,
O(N logN + N/B)Equality on non-key of s일 때,
O(N logN + TN/B)
4) Merge Join
r과 S가 정렬이 되어 있다고 가정하는 것
O(N/B)
정렬이 안되어있을 경우 정렬을 해야 하므로
O(N/B log_M/B(N/B))
5) Hash Join
equi join에서만 사용 가능
O(N/B)
메모리에 들어가지 못해 쪼개야 할 경우
O(N/B log_M/B(N/B))