Index
Index는 내가 원하는 Record의 위치를 가리키고있는 date Structure를 말한다.
이 Index는 다음과 같은 Record로 구성된 하나의 File이다

여기서 Search key는 찾을 대상을 구분하는 역할을 하고 Pointer는 해당 Record의 실제 위치를 가리키고 있다.
즉, 한 File의 Record의 각각의 Field(Attribute)는 Search Key의 역할을 할 수 있고, 이것에 대한 Index File이 존재 할 수 있다는 것이다.
물론, Insertion이나 Deletion과 같은 Data Base의 Update에 있어 Index File도 추가적으로 Update해주어야 하므로 관리 비용이 존재하긴 한다.
하지만, Data Base의 주된 사용 목적은 Search이다. 즉, 데이터만 Memory에 저장하는 것이 아니라 이 Index file도 함께 저장해야 원하는 Data를 빠르게 찾을 수 있다.
index 평가요소
- Access Time
: Data를 얼마나 빨리 찾을 수 있는지
- Insertion Time
: Data를 Insertion할 때 걸리는 시간
- Deletion Time
: Data를 Deletion할 때 걸리는 시간
- Space Overhead
: Index File의 크기를 얼마나 줄였는지
Index의 종류
1. Ordered Index
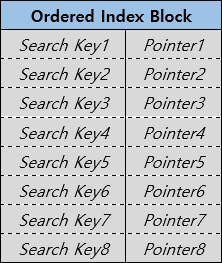
위의 그림과 같이 Entry가 Search Key의 순서대로 정렬되어 있는 Block으로 구성된 Index File을 의미한다.
또, 이 Ordered Index에서 대상 Data File은 Sequential File임을 가정하고 설명할 예정이다.
1) Primary VS Secondary
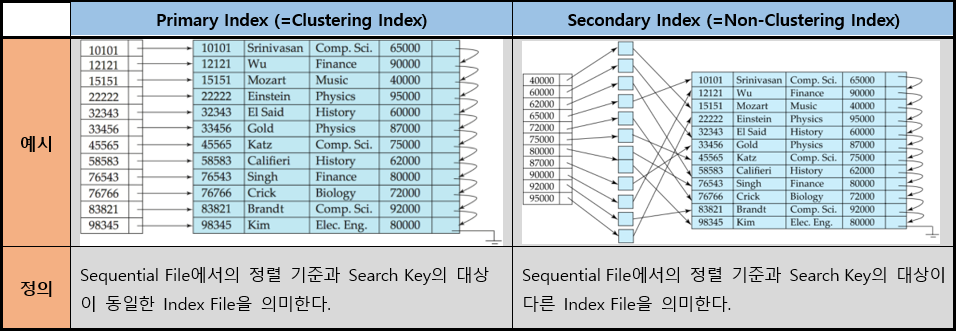
Relational DataBase에서
- Secondary Index는 다양한 조건을 통한 데이터 검색을 위해서는 반드시 필요하다.
- 보통 이 Primary Index가 Relation의 Primary Key가 되긴 하지만
반드시 Primary Key가 되어야 하는 것은 아니다.
Sequential Data File에 대해 Primary Index File이 존재할 경우
Index-Sequential file이라고도 한다.
Sequential Scan시 I/O Complexity
- Primary Index의 경우,
: Data File과 정렬 순서가 일치하므로 Sparse Index를 활용해
O(N/B)의 I/O Complexity 가 가능하다.
- Secondary Index의 경우,
: Data File과 정렬 순서가 다르기 때문에 Sparse Index를 활용할 수 없고,
O(N)의 I/O Complexity 가 발생하게 된다.
2) Dense VS Sparse

1. Sparse Index의 목적
Sparse Index를 사용할 경우 Index File의 크기를 효과적으로 줄일 수 있다.
이는, Index File조차도 Memory에 올라갈 수 없을 정도로 클 때 해결책이 될 수 있다.
2. Sparse Index가 Primary Index여야만 하는 이유
Data Block에 대해 대표값을 뽑기 위해서는 해당 Data Block이 우리가 원하는 Search Key에 대해 정렬되어있어야 할 것이다.
즉, Primary Index여야만 한다.
3. Multi Level Index
Sparse Index File을 층층이 쌓아 Multi Level Index File을 만들 수 있다.
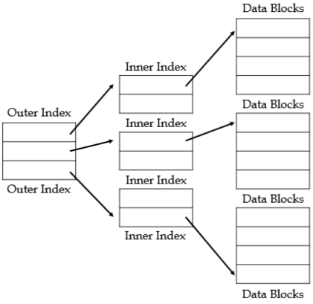
(Inner Index: Primary Index of Data File)
(Outer Index: Sparse Index of Primary Index)이때, 각 i번째 층은
N(i-1)/B(i-1)개의 Entry를 갖게된다.즉, 각 층마다 Block의 수를 1/B씩 줄일 수 있게되고,
이를 통해 Data에 접근하기 위해 Search할 Block의 수를 효과적으로 줄일 수 있다.
4. Multi Level Index의 단점
Search만 하는 DB의 경우 Multi Level Index는 단점이 없는 구조가 되지만 Update가 발생할 경우 문제가 발생하게 된다.
Data를 Delete/Insert할 때, Free Space가 많은 Data Block이 발생하게 된다.
즉, 대표값을 통해 Block Access횟수를 줄인다는 Sparse Index의 장점이 사라지게 된다.
따라서 주기적인 Reorganization이 필요하다.
3) Update
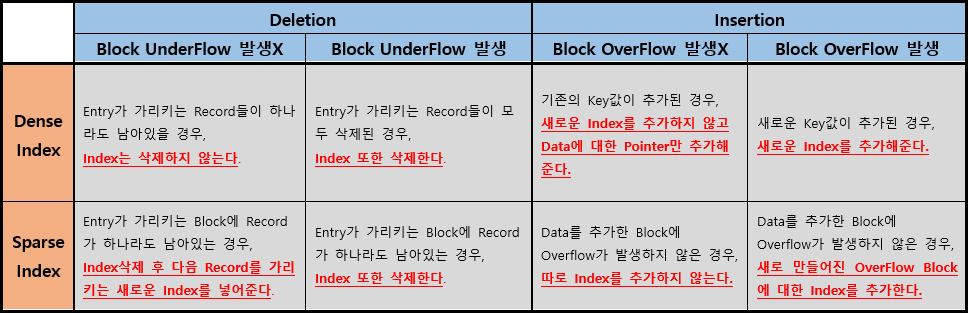
(주의점)
- Ordered Index이므로 Insertion의 경우 순서가 유지되도록 알맞은 자리를 찾아 Insertion을 수행해주어야 한다.
- Multi Level Index의 경우 OverFlow나 Under Flow가 Propagate될 수 있음을 주의해야 한다.
- 단순 Update의 경우, Deletion과 Insertion을 동시에 한다고 생각하면 된다.
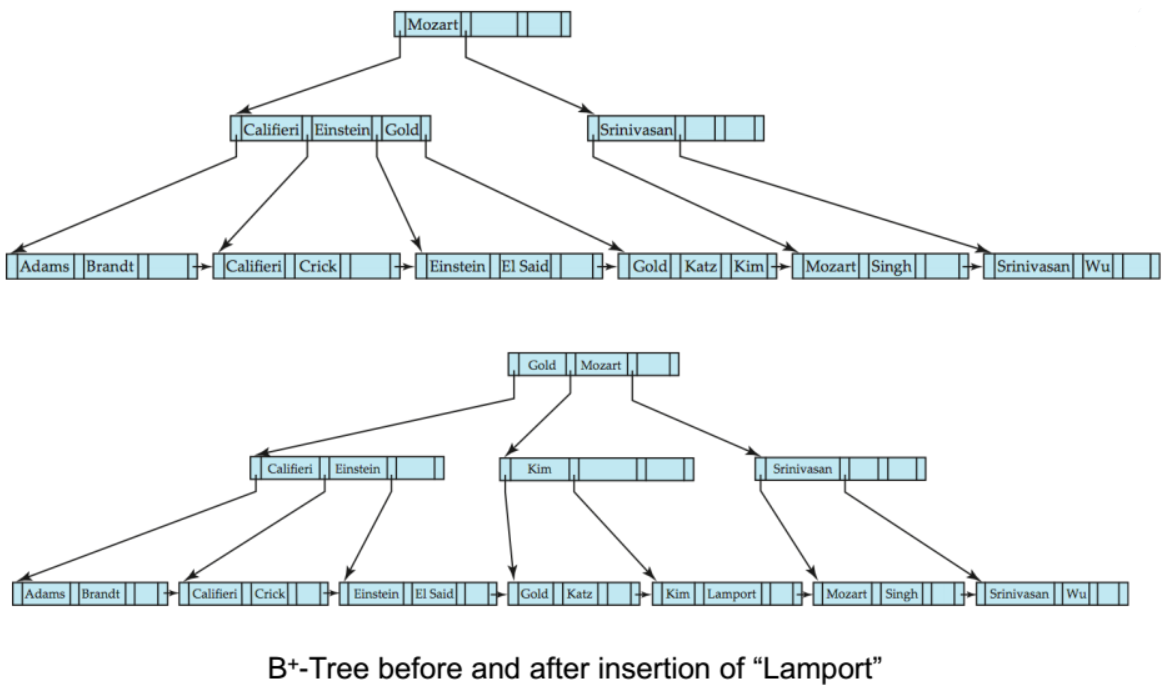
2. B+ Tree Index

위의 그림과 같은 Index Block들을 특정 규칙에 따라 연결한 Index File을 의미한다.
이 B+ Tree는 Data File이 Update가 자주 발생하면, 단점이 극대화 되는 Index-Sequential File을 대체하기 위해 사용되어진다.
Index-Sequential File와는 다르게 B+ Tree는 값싼 연산을 통해 Insertion이나 Deletion이 일어날 때마다 Reorganized를 해주기 때문에 애초에 그런 상황이 발생하지 않게된다.
1) 구조
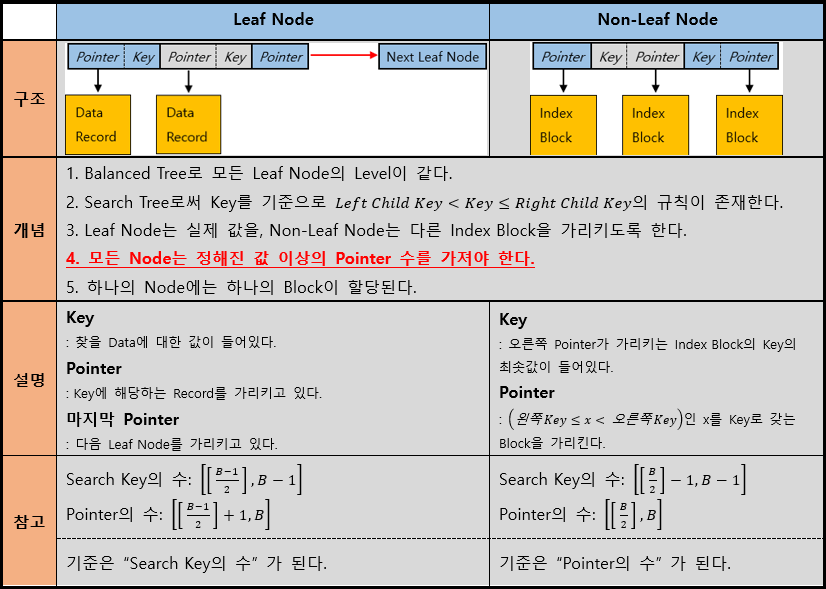
(여기서 B는 한 Node(Block)에 들어갈 수 있는 Pointer의 최대 개수를 의미한다.)
B+ Tree는 4번 규칙을 통해 Index-Sequential File의 단점을 극복할 수 있었다.
(참고사항)
- Root Node에 대해서는 Pointer 수에 대한 기준이 예외적으로 존재한다.
:[2, B]
- N개의 Data에 대한 Height는 다음과 같이 구할 수 있다.
(즉, 최악의 경우에는 B를 B/2로 바꾼 Height를 갖게 된다.)
2) Search
- Point Query
- 방법
: Search Tree임을 활용해 Leaf Node까지 이동하면 찾을 수 있다.- Complexity
:O(Log_B(N))의 I/O Complexity를 갖는다.(
Height+1번 Block에 접근하게 된다. )
(T개의 Record를 찾고자 할 때,)
- Range Query
- 방법
: Point Query를 활용해 최솟값을 찾아 data를 Return하고,
Leaf Node를 쭉 훑으면서 최대값이 나오기 전까지 Data를 Return한다.- Complexity
:O(Log_B(N) + T/B)의 I/O Complexity를 갖는다.(
Height+1+(T/B)번 Block에 접근하게 된다. )
3) Update

(참고)
- 일단 Leaf Node에 Insertion/Deletion을 수행하고 이것이 Propagate될 경우,
Non Leaf Node에서의 Insertion/Deletion을 수행한다.
- Merge 후 OverFlow가 발생해 다시 Split하는 것을 Redistribute 라고 한다.
(주의점)
- Root 가 Split 되는 경우는 Height가 증가할 때 뿐이다.
Height가 증가한 경우는 Root가 Split되었을 때 뿐이다.
- OverFlow와 UnderFlow는 Parent로 Propagate될 수 있다.
Update 예시
4) Secondary Index에 대해
B+ Tree는 Update에 Cost가 발생한다는 단점이 있었다.
이때 Primary Index는 어쩔 수 없지만, B+Tree로 구현된 Secondary Index는 Data자체를 Indexing하는 것이 아니라 Primary Index를 Indexing하므로써, Update의 Cost를 없앨 수 있다.
3. B- Tree Index
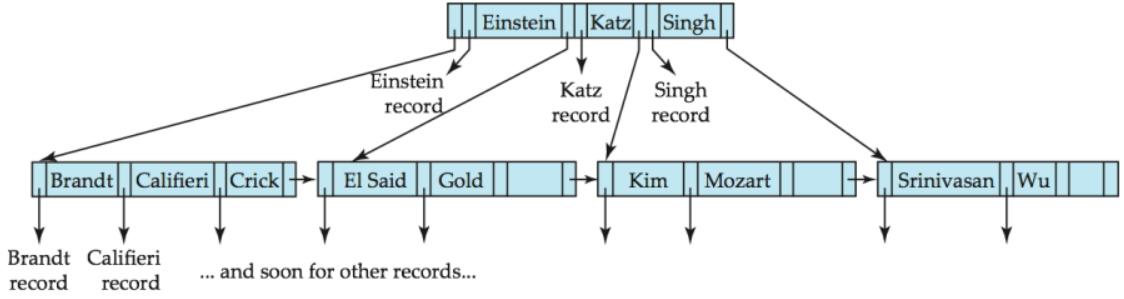
(자세한 내용은 다음을 참조)
1) B+Tree와의 차이점
모든 값이 Leaf Node에 있는 B+Tree와는 다르게 B-Tree는 Non-Leaf Node에도 값이 존재한다.
따라서 Non-Leaf Node에서는 Record를 가리키기 위한 포인터와 Child를 가리키는 포인터, 총 2개의 포인터가 필요하게 된다.
2) 장단점
단점
- 포인터가 2개씩 저장되므로 저장되는 데이터의 크기가 커질수록 height가 B+ Tree보다 높아질 가능성이 있다.
- Range Search가 불가능하다.
장점
- leaf node까지 도달하기 전에 원하는 Record를 찾을 가능성이 있다.
(그러나 Tree의 특성상 그 확률은 낮다.)
Multi Key Access
여러 Index File을 활용해야 하는 경우 다음과 같은 방법을 사용할 수 있다.
-
먼저 하나의 Index File로 Data를 검색한다.
그리고 그 결과에 대해 나머지 조건을 Sequential하게 검사한다. -
각각의 Index File로 Data를 검색한다.
그리고 그 결과의 교집합을 구한다. -
Index File의 Dememsion을 늘려 다시 만든다.
(학부생 수준 X)