머신러닝

1. 개요

1) 동작 과정

입력
: 데이터

모델
: svm, random forest등
: deep learning 모델

출력
: 데이터로부터 생성할 수 있는 정보

2) 학습 과정

모델이 가지고 있는 파라미터를 수정해 나아가는 과정

---

파라미터를 수정하기 위해 정해야 할 것
1. 모델
2. loss function
: 데이터를 우리의 모델로 가공한 결과와, 실제 생성했어야 할 결과에 대한 차이를 어떻게 규정할 것인지ㅣ 정해야 ㅎ함

---

학습
모델을 규정짓는 파라미터를 수정해 나가면서 우리가 정한 loss가 최소화 되는 파라미터를 찾는 과정

2. Loss Function

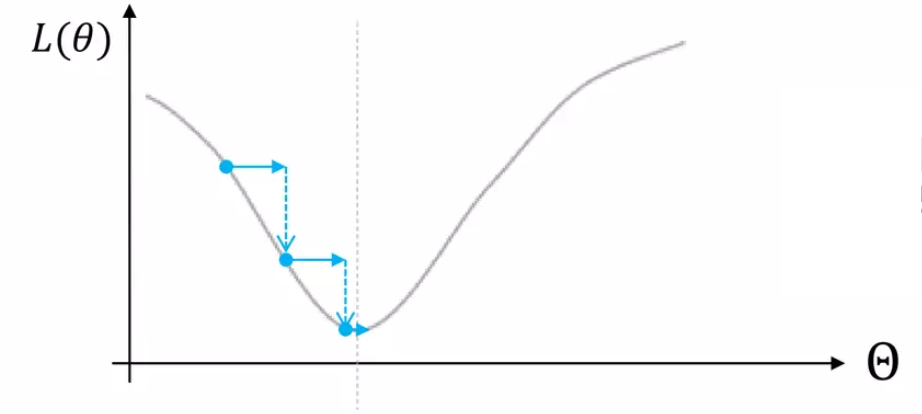
1) Loss Function의 조건

이미 Deep Learning을 배웠던 사람들이라면 다음의 가정들은 당연하다고 생각할 수 있다.

우리는 언제나 그렇듯 당연한 만큼 소홀이 할 수 있기 때문에 한번 더 짚고 넘어가자.

---

1. Loss를 구할 때에는 네트워크의 최종 출력과 정답만을 가지고 구해야 한다.

$L(f_\theta(x), y)$

즉, 네트워크의 중간 출력값을 통해서 Loss Function을 구성할 수는 없다는 것이다.
(후에 GoogleNet이라는 딥러닝 모델을 배울 때, 이 부분을 유의해서 공부해 보자)

---

2. 학습 데이터 전체에 대한 Loss값은, 각각의 학습 데이터의 Loss값의 합과 같다.

$L(f_\theta(x), y) = \displaystyle\sum_{i}L(f_\theta(x_i), y_i)$

$f$: 모델
$\theta$: 모델의 파라미터
$x$: 입력(학습) 데이터
$y$: 모델이 실제로 생성했어야 하는 출력

2) Loss Function의 종류

mse, rmse

cross entropy

Label Smoothing

focal loss

dice loss

3. Back Propagation

1) Gradient Descent

Loss Function을 정하고 난 후 우리는 어떻게 이 Loss값을 줄일 수 있는지 정해야 한다.

이 방법에 대한 힌트는 Taylor Expansion에서 부터 시작한다.

---

1. Taylor Expansion

우리가 잘 알고 있는 Taylor Expansion의 수식은 위와 같다.

여기서 $x=a+\Delta a$라고 하면,
$f(a + \Delta a)-f(a) = \nabla f \Delta a + \frac{\nabla^2f\Delta a^2}{2!} + ...$ 라고 다시 쓸 수 있다.

이제 $a$를 $\theta$, 그리고 $f$를 $Loss function$ 로 다시 생각해 보고 우항의 1번째 항까지만 사용하여 근사한다면,

$L(\theta + \Delta \theta)-L(\theta) = \nabla L \Delta \theta$ 이다.

이때, 우리는 모델의 파라미터 $\theta$를 바꾸었을 때, 전체 Loss값이 음수가 되기를 원한다.

즉, $\Delta \theta = -\eta \nabla L$ 로 설정한다면,
$L(\theta + \Delta \theta)-L(\theta) = -\eta ||\nabla L ||^2$ 이 되어 항상 음수가 된다는 것을 알 수 있다.

(참고)
:Taylor 급수를 근사하여 구한 것이 위 식이기 때문에 위의 식은 항상 맞아 떨어지는 것이 아니라 $\Delta \theta = 0$에 근사할 때에만 성립하게 된다.
즉, 우리는 이를 위해 learning rate라고도 불리는 적절한 $\eta$의 값을 설정해 위의 식이 성립하도록 해 주어야 한다.

---

2. Gradienta Descent

위의 Taylor 급수를 통해 우리는 $\Delta \theta$를 $-\eta \Delta L$로 설정해야 한다는 것을 알았다.

이제 우리는 다음과 같은 과정을 통해 Loss Function을 Update하며 나아가 보자.

• $L(\theta_k, x) = \sum_i L(\theta_k, x_i)$
  : (Loss Function에 대한 조건 2로 인해 성립한다.)

• $\nabla L(\theta_k, x) = \sum_i \nabla L(\theta_k, x_i) \overset{\triangle}= \sum_i \frac{ \nabla L(\theta_k, x_i)}{N}$
  : N은 전체 학습 데이터의 수 이고, N으로 나눈다고 해도 Loss값이 음수가 된다는 사실은 변하지 않기 때문에 나누어 주어도 상관 없을 것이다.

---

3. 결론

즉, 우리는, 학습을 위해서

• $\nabla L(\theta_k, x) = \sum_i \frac{ \nabla L(\theta_k, x_i)}{N}$ 구하기

• $\theta_{k+1} = \theta_k - \eta \nabla L(\theta_k, x)$ 구하기

위의 두 과정을 통해 현재 모델의 파라미터 $\theta$를 업데이트 해 나아갈 수 있을 것이다.

2) Back Propagation

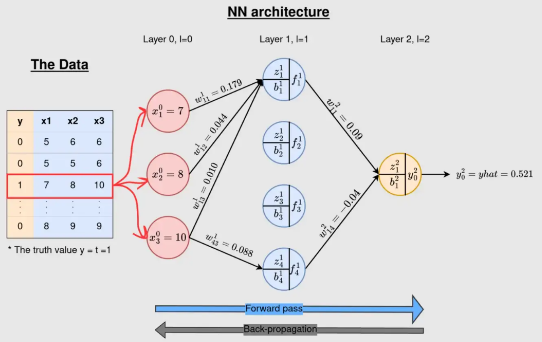
인공지능의 역사를 보면 크게 2번의 침체기가 있었다. 이를 인공지능의 겨울이라고 한다.

이 중 1번째 겨울은 XOR Problem에 의해 발생하였는데, 뉴런이 직선으로 밖에 표현되지 못해 나타나는 문제였다.

이 문제는 Activation Function이라는 비 선형 함수의 도입으로 해결할 수 있었지만, Gradient Descent를 사용하기 위해 미분을 할 때 매우 많은 연산량이 발생하였기 때문에 이것 만으로는 사용할 수 없었다. 이 문제를 해결한 것이 다음의 Back Propagation Algorithm이다.

---

1. Chain Rule

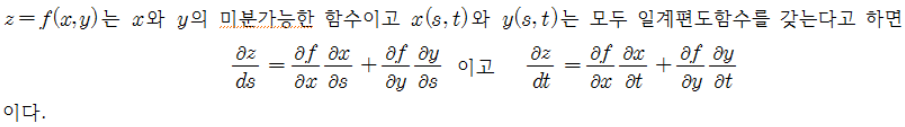
(연쇄법칙 증명)

---

2. Back Propagation

---

(참고페이지)

4. Maximum Likelihood

1) Loss Function을 보는 관점

다양한 Loss Function들이 존재한다.
이때, Loss Function을 어떤 것으로 정해야 하는가? 에 대한 것은 크게 다음의 두 관점에서 대답되어 진다.

---

1. BackPropagation의 동작

Cross Entropy > MSE

---

2. 출력값이 Continuous한가

(==Maximum Likelihood관점)

Network 출력값이 Continuous하다
MSE > Cross Entropy

discrete하다 (ex. classification)
Cross Entropy > MSE

위 내용은 이활석님의 오토인코더의 모든 것 -1/3의 강의를 참고하였습니다.

hard nevative mining