1) 순차탐색과 이진탐색

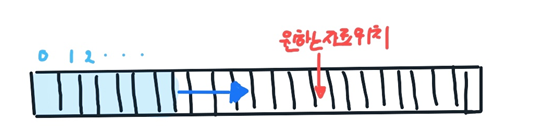
어떤 저장공간에서 자료를 찾을 때 원하는 자료를 찾는 방법은 여러가지가 있다. 이 중 가장 간단한 방법은 당연히 단순히 앞에서 부터 차례대로 찾아보는 방법일 것이다. 이 방법을 순차탐색이라고 한다.

이 때 순차탐색은 간단하지만, 앞에서부터 모든 데이터를 하나하나 확인해야 하므로 시간이 오래 걸린다는 단점이 존재한다.

순차탐색

for(int i = 0; i < v.size(); i++) {
    if(v[i] == x)
        ~(찾음)~;
}

즉, O(n)의 시간복잡도를 가진다.

이렇게 순차탐색의 시간 문제를 해결해 줄 수 있는 방법으로 이진 탐색이라는 방법이 존재한다.

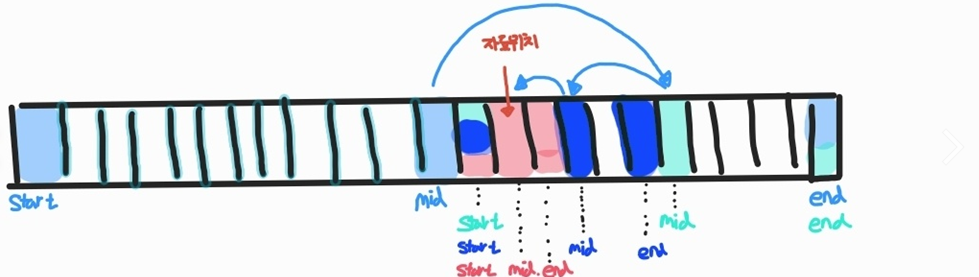
이진 탐색이란 정렬되어 있는 배열에서 중간값을 확인해 가면서 원하는 자료의 위치에 접근하는 방법이다.

비록 정렬되어 있어야 한다는 단점이 있지만, 이 상황에서 시간을 매우 단축시켜 준다는 장점이 있어 실제 문제에서도 유용하게 사용된다.

이진탐색

int start = 0;     int end = v.size() - 1;
while(start <= end) {
    int mid = (start + end)/2;
    if(v[mid] < x)
        start = mid + 1;
    else if(v[mid] > x)
        end = mid - 1;
    else
        ~(찾음)~;
}

즉, O(log n)의 시간복잡도를 가진다.

2) 이진탐색 구현

먼저 이진탐색을 사용할 때 우리는 해당 배열에서 어떤 부분을 찾을 것인지 정해야 한다.

즉, 배열에서 x라는 원소를 찾고자 할 때 다음의 두 경우를 생각해 볼 수 있을 것이다.

• 배열에서 x이상인 원소가 처음 나오는 위치.
  ( == 배열에서 x가 처음 나오는 위치)

• 배열에서 x를 초과하는 원소가 처음 나오는 위치
  ( == 배열에서 x보다 큰 원소가 처음 나오는 위치)

위와 같이 경우의 수를 정할 경우, 만약 x가 존재하지 않는다고 하더라도 처리할 수 있는 함수가 될 것이다.

Lower_bound 구현

위의 두 경우에서 첫번째 경우를 lower_bound 위치라고 한다.

int Lower_Bound(vector<int> v, int target) {
    int start = 0;
    int end = v.size()-1;
    while (start < end) {
        int mid = (start + end) / 2;
        if(v[mid] < target)
            start = mid + 1;
        else
            end = mid
    }
    return end;
}

위의 방법 외에도 아래와 같은 방법을 사용할 수도 있다.

int Lower_Bound(vector<int> v, int target) {
    int result;
    int start = 0;
    int end = v.size()-1;
    while (start <= end) {
        int mid = (start + end) / 2;
        if (v[mid] < target)
            start = mid + 1;
        else {
            end = mid - 1;
            result = mid;
        }
    }
    return result;
}

#include <algorithm>  
int Lower_Bound(vector<int> v, int target) {
    return lower_bound(v.begin(), v.end(), target)
  		   - v.begin();
}
/* lower_bound(시작주소, 끝주소, 찾을원소)
  반환형은 Iterator로 실제 위치를 알고 싶으면
  시작주소를 빼주어야 함 */

Upper_bound 구현

두번째 경우를 upper_bound 위치라고 한다.

int Upper_Bound(vector<int> v, int target) {
    int start = 0;
    int end = v.size()-1;
    while (start < end) {
        int mid = (start + end) / 2;
        if(v[mid] <= target)
            start = mid + 1;
        else
            end = mid
    }
    return end;
}
/* Lower_bound랑 다른점은 
  v[mid] < target 이 부분이
  v[mid] <= target 로 바뀌었다는 부분뿐이다.*/

마찬가지로 위의 방법 외에도 다음과 같은 방법을 사용할 수 있다.

int Upper_Bound(vector<int> v, int target) {
    int result;
    int start = 0;
    int end = v.size()-1;
    while (start <= end) {
        int mid = (start + end) / 2;
        if (v[mid] <= target) {
            start = mid + 1;
            result = mid;
        }
        else
            end = mid - 1;
    }
    return result + 1;
}

#include <algorithm>  
int Upper_Bound(vector<int> v, int target) {
    return upper_bound(v.begin(), v.end(), target)
  		   - v.begin();
}
/* upper_bound(시작주소, 끝주소, 찾을원소)
  반환형은 Iterator로 실제 위치를 알고 싶으면
  시작주소를 빼주어야 함 */

문제

• 백준 1654번, 랜선 자르기
• 백준 1920번, 수 찾기
• 백준 2470, 두 용액
• 백준 10815, 숫자 카드
• 백준 3745, 오름세
• 백준 1561, 놀이공원
• 백준 3079, 입국심사
• 백준 1365, 꼬인 전기줄
• 백준 7795, 먹을 것인가 먹힐 것인가
• 백준 2343, 기타 레슨
• 백준 16434, 드래곤 앤 던전
• 백준 8983, 사냥꾼
• 백준 3649, 로봇 프로젝트
• 백준 11053, 가장 긴 증가하는 부분 수열
• 백준 12738, 가장 긴 증가하는 부분 수열 3