Matrix Factorization

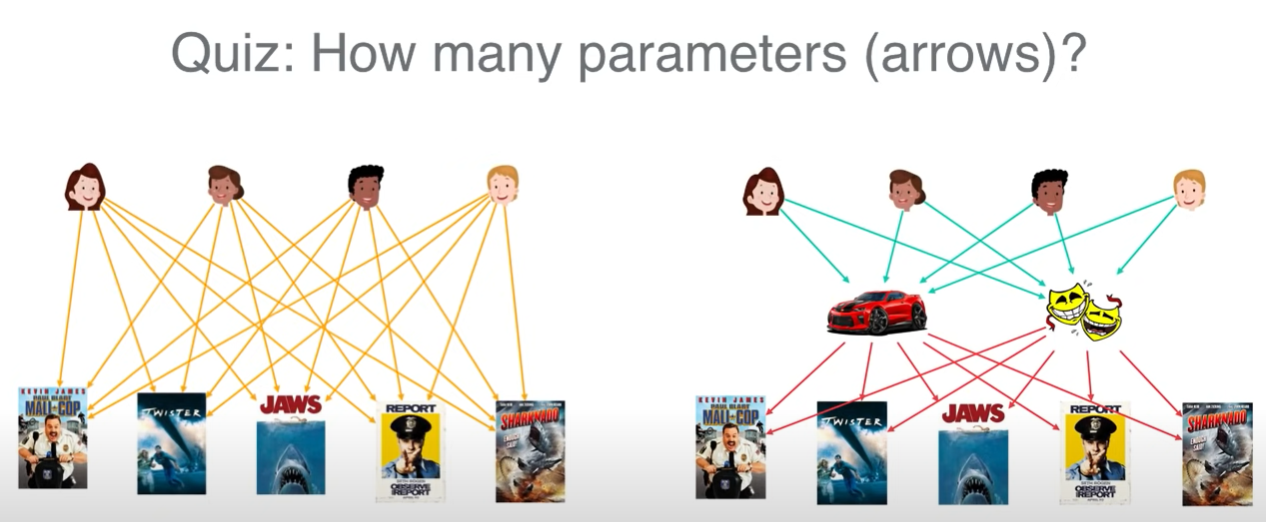
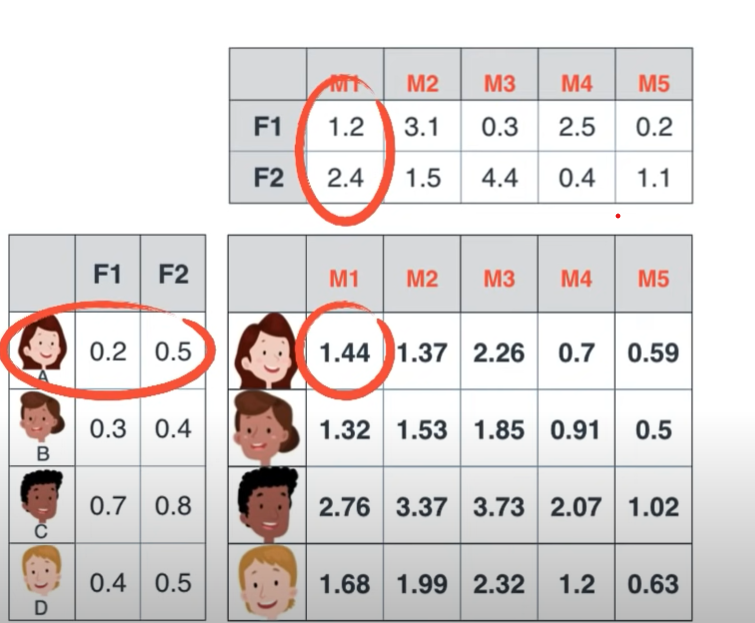
잠재 요인이 분명 있을 것이다. 무엇인진 알 수 없지만, 잠재 요인 (사진에서는 2개로 가정)에 대응되는 유저의 가중치, 그리고 영화의 특성 값을 찾아내는 것이 목적이다.

SVD

특이값 분해를 이용하여 행렬을 분해하는 알고리즘이다.
하지만 이론적인 배경이 될 뿐 특이값 분해는 머신러닝이 아니다.

우선 NAN값들을 전부 초기화 해 주어야 분해가 가능한데, 우리의 목표는 NAN값을 예측하는 것이다. 순서가 바뀌었다.

그리고 학습의 개념이 아닌, 그저 행렬을 분해할 뿐이다. 다시 합치면 당연히 원본 행렬이 그대로 나오게 된다.

다만 드물게 존재하는 매우 DENSE한 행렬에 대해서는, NAN값을 예측하는 추천시스템으로서가 아닌, 개개인의 LATENT FACTOR에 대한 PARAMETER들을 추출하는 목적으로 사용할 수 있다.

Gradient Descent

비용함수를 정의하고, 비용함수를 기반으로 최적화를 하게 된다. Stochastic Gradient Descent 및 ALS(Alternating Least Squares) 기반의 training 방법이 있다.

Cost Function

우선, 데이터가 존재하는 elements들에 대해서만 latent factor들의 내적과 실제 값 사이의 오차제곱합으로 정의된다. (binary label의 경우는 logistic loss)

여기에 bias, mean normalization, regularization 등을 더 적용할 수 있다.

직접 미분함수를 계산해서 각각 parameter들에게 편미분 값을 빼줄 수 있겠지만, 딥러닝 프레임워크를 사용하면 numerical derivation을 통해 편미분 계산 없이 gradient descent를 수행할 수 있다.

$\min_{q, p, b} \sum_{(u,i) \in K} (r_{ui} - \mu - b_{i} - b _{u} - q_{i}^{T}p_{u}) ^ 2 + \lambda ( \| q_{i} \|^2 + \| p_{u} \|^2 + b_{i}^2 + b_{u}^2 )$

(regularization, bias, normalization 모두 적용)

Stochastic Gradient

전체 데이터셋의 일부를 추출하여 전체 Cost Function에 대한 가정 없이 gradient descent를 적용함.

Alternating Least Squares

일반적으로

$(x - a )^2$

의 형태에서 x가 단순 변수이면 convex하지만

$\min_{q, p} \sum_{(u,i) \in K} (r_{ui} - q_{i}^{T}p_{u}) ^ 2 + \lambda ( \| q_{i} \|^2 + \| p_{u} \|^2 )$

와 같은 함수에서는 p와 q가 모두 변수이기 때문에 convex함을 보장할 수 없다. 하지만 p나 q 하나를 고정하게 되면 convexity가 보장된다.

따라서 p,q를 번갈아가면서 고정하고 gradient descent를 수행하는 방식이다.

Factorization Machine

Matrix Factorization은 structured data에만 적용할 수 있다. (예 : 영화 평점, 영화 시청 여부, 광고 클릭 여부 등)

sparse한 데이터에 대해 예측 성능이 떨어진다.

SVM과 Matrix Factorization의 장점을 합한 FM은, 오히려 다항회귀에 가깝다.

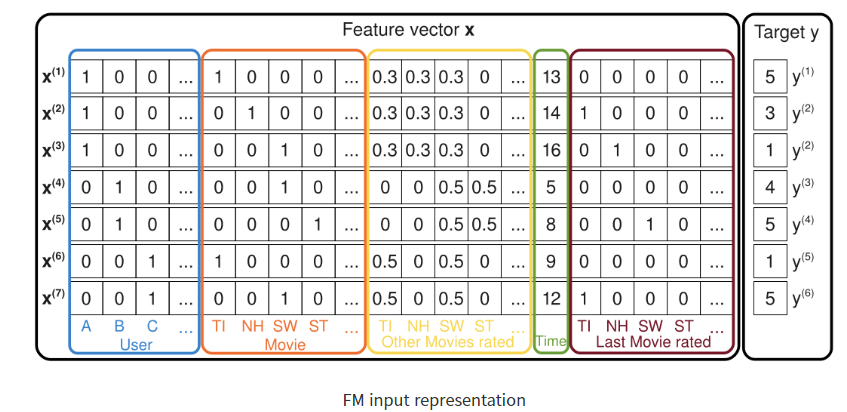
위 그림에서 볼 수 있듯이, 유저 아이템 간의 rating 정보만 사용하던 MF와 달리 다양한 피쳐들을 인풋 데이터로 넣을 수 있다. 원하는 대로 Feture Engineering을 한 후, 궁극적으로 target데이터는 이전과 같이 rating이다.

피처 엔지니어링을 통해 차원을 마구 높여주는 것이 마치 SVM과 비슷하다.

단순 선형 회귀?

$\widehat{y}(x) = w_{0} + \sum_{i=1}^{n} w_{i}x_{i}$
$w_{0} \in \mathbf{R}, w \in \mathbf{R^n}$

선형 관계이면 좋겠지만, 그럴리가 없다.
두가지 해결책이 있다.

poly regression and neural network !

다항 회귀

$\widehat{y}(x) = w_{0} + \sum_{i=1}^{n} w_{i}x_{i} + \sum_{i=1}^n \sum_{j=i+1}^n W_{ij}x_{i}x_{j}$
$w_{0} \in \mathbf{R}, w \in \mathbf{R^n}, W \in \mathbf{R^{nxn}}$

2차 3차 항까지 다양하게 넣을 수 있겠지만, 우선 기본적으로 서로 다른 두 변수간의 관계를 나타내는 항까지 추가해주자. 그럼 학습해야 할 parameter는 다음과 같다.

$w_{0}$, $\overrightarrow{w_i}$, $\bold W_{ij}$

그런데 $W_{ij}$ 에서 재밌는 성질을 발견할 수 있다. 우선 당연히 symmetric matrix이므로,,

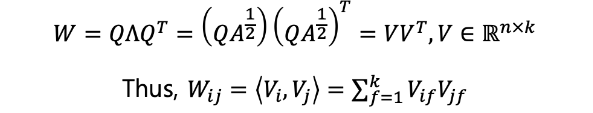
이고 아래와 같이 표현할 수 있다.

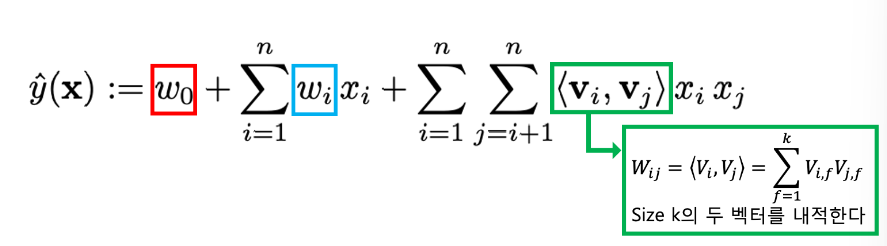
일반적인 다항회귀를 적용하게 되면 모든 parameter를 일일이 gradient descent 하게 되고, $O(N^2)$의 time complexity를 갖게 된다.

하지만 SVM의 Kernel Trick like한 위 방식을 적용해 Wij 계수들을 embedding vector간의 내적으로 계산하게 되면, $O(N*K) = O(N)$ 의 linear time complexity를 갖게 된다!

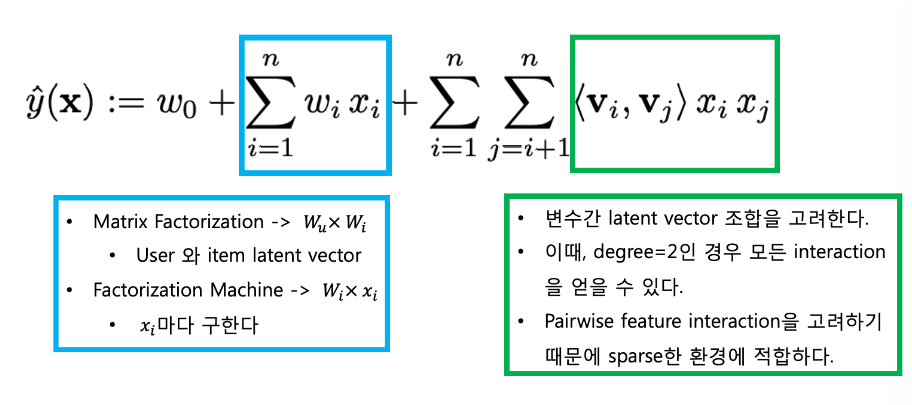
• 2차원으로만 확장했는데, n차원으로 확장?
  -> 이론적으로 가능하고, 여전히 linear complexity
  

Neural Network

추후에..

References

• supkoon님의 블로그
  Matrix Factorization
  Factorization Machine
• Youtube
  matrix factorization(youtube)