이번 문제는 크루스칼 알고리즘을 활용한 최소신장트리를 찾는 문제입니다.
알고리즘만 알고있으면, 쉬운문제로 해당 문제를 활용한 문제를 하나 또 풀어봐야겠습니다.
최소신장 트리를 구하는 문제인지, 아닌지는 판단하기 굉장히 쉽습니다.
왜냐하면, 다익스트라, 벨만포드, 플로이드 와샬은 일단 노드에서 노드까지의 최솟값을 구하는 문제입니다.
그러나, 최소신장 트리는, 최종적으로 모든 노드를 연결했을때 가장 적은 비용으로 연결한 그래프를 구하기 위한 알고리즘입니다.
예를 들어 통신망을 구축할때, 모든 기지국을 연결하면서 도로의 길이가 최소가 되도록하는 문제와 같습니다.
MST의 특징으로는
-
간선의 가중치 합이 최소여야한다.
-
N개의 정점이 있으면, 그래프를 만들때 n-1개의 간선만을 사용해야한다.
-
이는 2번 내용의 연장으로 사이클이 포함되서는 안된다.
당연히 사이클이나 n-1개 이상의 간선을 사용하면 안되는게, 최소로 모든 노드를 연결한 그래프를 그리는데, N개 이상을 사용하거나 사이클이 생성되는 그래프를 그리면, 그 가중치가 최소가 아닌게 당연하기 때문이다.
고로, 해당 MST 생성 방식은
-
간선의 가중치를 오름차순으로 정렬한다.(최소 가중치를 구해야하니까)
-
간선들을 연결하면서 사이클 생성 유무를 판단한다. (사이클 생성 유무는 Union Find를 사용한다.)
-
사이클이 생성된다면, 넘긴다.
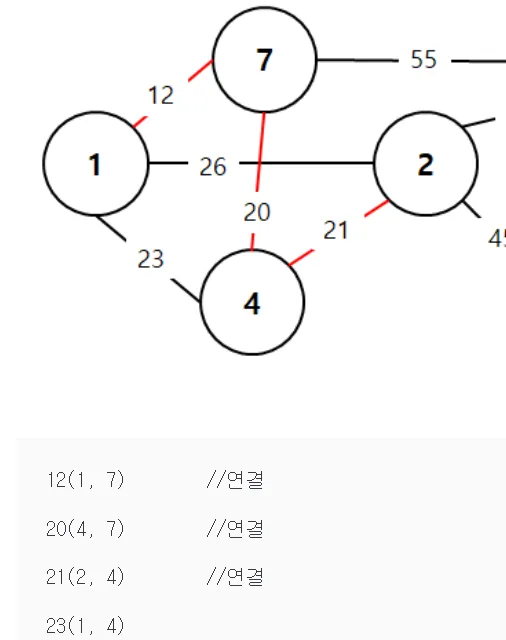
예를 들어, (1,7)노드를 연결하고, (7,4)노드를 연결하고 (1,4)노드를 연결하려 했는데 사이클이 발생하므로, 무시하고 넘어갑니다.
이렇게 하는 이유는, 이미 2개의 간선을 사용하여서 1,7,4번 노드를 모두 최소값으로 방문할 수 있는데 1,4노드를 연결하는 간선을 추가할 이유가 없기 때문입니다.
int main() {
int vertex, e;
cin >> vertex >> e;
int result = 0;
vector<pair<int, pair<int, int>>>v;
for (int i = 0; i < e; i++) {
int from, to, cost;
cin >> from >> to >> cost;
v.push_back({ cost,{from,to} });
}vertex는 노드, e는 간선입니다.
v 벡터에는 첫번째가 cost, 두번째 벡터가 from,to 입니다.
예를 들어 12,{1,7}이 됩니다.
그 다음에, sort메서드를 통해 정렬합니다.
그래야 그리디로, 최소경로를 구할 수 있으므로
sort(v.begin(), v.end()); Union Find를 사용하기 위해서 부모를 자기 자신으로 초기화
for (int i = 1; i <= vertex; i++)parent[i] = i;for (int i = 0; i < v.size(); i++) {
if (!sameparent(v[i].second.first, v[i].second.second)) {
uni(v[i].second.first, v[i].second.second);
result += v[i].first;
}
}해당 로직은 v.size()에는 경로가 들어있으니까, 최소 cost에 있는 from과 to를 꺼내서 부모가 동일한지 확인합니다.
만약 동일하다면, pass, 동일하지 않는다면, uni를 호출하여서 merge를 해줍니다.
그리고, result라는 최종 결과에다가 cost를 더해줍니다.
//유니온 파인드에서 썻던 부모 찾는 함수
int find(int x) {
if (parent[x] == x)return x;
else return parent[x] = find(parent[x]);
}
//부모 동일하게 merge해주는 함수
void uni(int x, int y) {
x = find(x);
y = find(y);
parent[y] = x;
}
//사이클 발생하는 지 유무를 따지기 위함
bool sameparent(int x, int y) {
x = find(x);
y = find(y);
if (x == y)return true;
else return false;
}sameparent는 만약 1,7번 노드가 들어왔다면, find메서드를 호출하여서 해당 정점의 부모를 찾습니다.
같다면, true, 다르면 false를 반환합니다.
find는 재귀함수로, 부모를 찾으면 자기 자신을 반환합니다.
왜냐하면, 모든 부모는 자기 자신이기때문입니다.
만약 parent 배열에서
1 7 3
1 1 3
에서, 7번과 3번을 연결하려면
7번의 부모는 parent[7]=1이므로 find(1)다시 호출 1 반환
그리고 3번의 부모를 1로 바꿔줍니다.
왜냐하면 uni메서드의 parent[y]=x이기 때문입니다.
전체 코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int parent[10001];//사이클 판별을 위한 배열
//유니온 파인드에서 썻던 부모 찾는 함수
int find(int x) {
if (parent[x] == x)return x;
else return parent[x] = find(parent[x]);
}
//부모 동일하게 merge해주는 함수
void uni(int x, int y) {
x = find(x);
y = find(y);
parent[y] = x;
}
//사이클 발생하는 지 유무를 따지기 위함
bool sameparent(int x, int y) {
x = find(x);
y = find(y);
if (x == y)return true;
else return false;
}
int main() {
int vertex, e;
cin >> vertex >> e;
int result = 0;
vector<pair<int, pair<int, int>>>v;
for (int i = 0; i < e; i++) {
int from, to, cost;
cin >> from >> to >> cost;
v.push_back({ cost,{from,to} });
}
//cost기준으로 sort해줘야한다.=>그래야 그리디로 최소 경로 구할 수 있음
sort(v.begin(), v.end());
//부모 초기화
★★★for (int i = 1; i <= vertex; i++)parent[i] = i;
//동일한 부모가 아닐때, merge해주고, result에다가 cost더하기
//아직 더하지 않은 간선은 앞에 부모를 자기 자신으로 초기화해서
//값이 자기 자신이다.즉 7,4를 연결할때 7은 부모가 1 이고 4는 부모가 4라는것이다.
//그다음에 4랑 1 이랑 연결하려하면 이제 부모가 1로 동일해서 건너뛴다.
for (int i = 0; i < v.size(); i++) {
if (!sameparent(v[i].second.first, v[i].second.second)) {
uni(v[i].second.first, v[i].second.second);
result += v[i].first;
}
}
cout << result;
}