문제 바로가기
이번 문제는 해당 글을 참고하고 풀었습니다.
이걸 어떻게 풀어야할지 감도 안잡혔는데, 위의 글을 보자 도대체 이런 풀이법은 어떻게 생각했을까? 자괴감이 드는 문제였습니다.
위의 글을 보고 이해가 안갈 수 있으니 저의 방법대로 3가지 전제 조건에 대해서 설명해 보도록 하겠습니다.
조건 1.
배달하거나 회수해야할 물건이 있다면 무조건 거기까지는 가야합니다.
예를들어
배달 1100
픽업 0004
이런식이라면, 3번과 4번집에는 배달을 할것이 없더라도 반드시 회수를 하기위해서 4번집까지 가야합니다.
그렇다면, 앞에서 부터 찾는게 좋을까요? 뒤에서 부터 찾는게 좋을까요?
당연히 해당문제에서 예시를 들어준것처럼 뒤에서 부터 찾는게 더 좋습니다.
당연히 그러한게, 뒤에서 부터 와야지 여러번 왔다갔다 하지 않을 수 있기 때문입니다.
조건 2.
배달과 회수는 독립적이다.
문제 예시 1번을 보면,
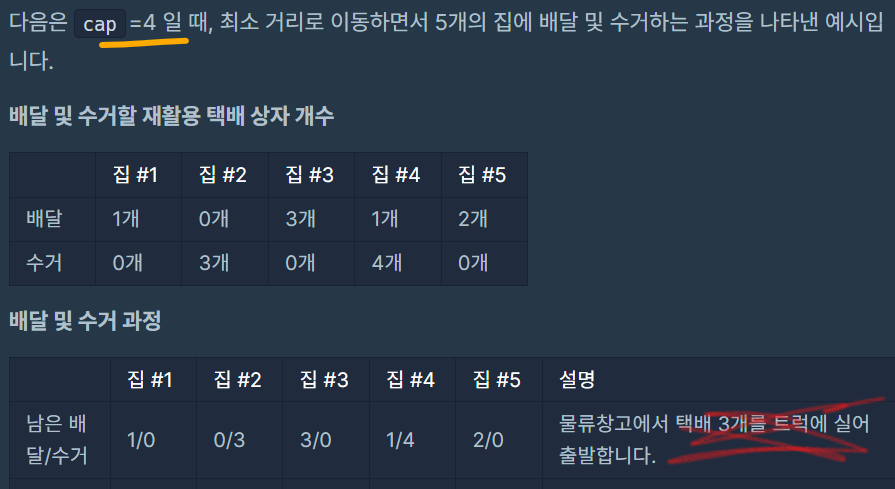
약간의 훼이크를 준게, 분명이 최대로 실을 수 있는게 4개인데도, 3개를 실어서 출발한다는 것입니다.
이는 틀렸습니다.
만약 배달해야하는 집이
00223 이고 cap이 3이면, 어차피 우리는 배달해야하는 집의 상자수를 알고 있기때문에,
최대로 배달 할 수 있는 만큼 실어서 출발하면 됩니다.
예를들어, 00223이고 cap이 3이므로 조건 1번에 의해 제일 먼 지점부터 배달을 해줄거니까 3개를 싫고 3개를 주면 됩니다. -> 00220
그다음에, 4번째 집이 2개를 배달해줘야하는데 cap이 3이므로 4번째 집에 2개를 주고 1개는 3번째 집에 주면 됩니다..
00100 이되면 여기서 중요한게, cap이 3이지만 이러면 1개만 실어서 출발해버리면 됩니다.
어? 그러면 여기서 약간 오해할 수 있는게 그러면 회수해야하는 상자도 고려해야하는데 배달과 어떻게 독립적이냐?
01100
00004
이런식으로 회수가 멀리 있는경우, 회수를 하기 전까지 배달해야하는 상자가 있다면(11) 그걸 배달하고 마지막에서 회수를 하면됩니다.
만약
00001
03000
이런식이면 1을 배달하고 돌아올때 3을 그냥 가져오면 됩니다.
이는 회수와 배달이 독립적임을 알 수 있습니다.
조건 3. 누적합 이용하기
그러면 아! 독립적인건 알겠다. 그런데 00005가 있고 cap이 3이면 무조건 5번 집에는 두번을 들려야한다.
그러면 나는 최대 배달할 수 있는 상자는 두번 왕복하니까 cap*2이므로 6개이다.
그렇다면 이를 어떻게 활용할 것인가 이다.
long long d=0;
long long p=0;
for(int i = n-1; i>=0; i--){
d-=deliveries[i];
p-=pickups[i];
int cnt =0;
while(d<0 || p <0){
d+=cap;
p+=cap;
cnt++;
}여기 for문을 보자.
00005에서 cap이 3이라면
5번집에가서 cap만큼 상자를 배달하면 00002가 된다. 그러면 무조건 2개를 더 배달하러 한번 더 출발해야한다.
그렇다면
첫번째 for문에서 d-=deliveris[i]를 통해서 d가 -5가 되고
cap만큼 더해준다. -2가 될것이다. 이는 2개를 더 배달하기 위해 무조건 한번 더 출발해야한 다는것이다.
그런데 우리는 cap개를 실을 수 있으므로
-2+3은 1이된다.
이말은
00015의 경우
00012가되고
내가 3개를 실고 출발할경우 1개를 4번째 집에도 줄 수 있다는 것이다.
이렇게 되면 for문의 다음번 인덱스인 i=4에서는 d가 1이므로 d-=1을 해줘도 d가 0이므로 while문을 들어가지 않는다.
이렇게 누적합을 이용한다.
answer로 더할때는 i번째 집에 해당하는 i+1에 왕복이니까 2를 곱하고 몇번 그 집을 방문했는지 cnt를 곱하면 정답이 된다.
정답코드
#include <string>
#include <vector>
using namespace std;
long long solution(int cap, int n, vector<int> deliveries, vector<int> pickups) {
long long answer = 0;
long long d=0;
long long p=0;
for(int i = n-1; i>=0; i--){
d-=deliveries[i];
p-=pickups[i];
int cnt =0;
while(d<0 || p <0){
d+=cap;
p+=cap;
cnt++;
}
answer += (i+1)*2*cnt;
}
return answer;
}굉장히 어려웠던 문제이다.
마지막에서 시작하는것은 알겠는데,
배달과 회수가 분리되어있다는점을 고려하면 답을 보면 쉬웠던 문제이다.
